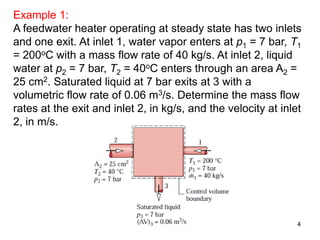
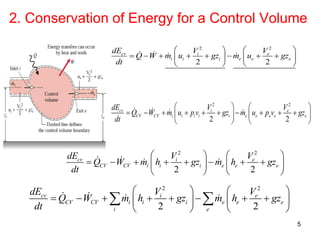
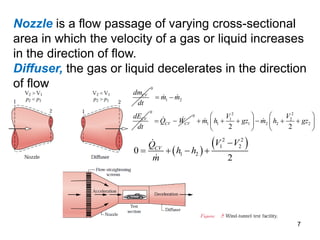
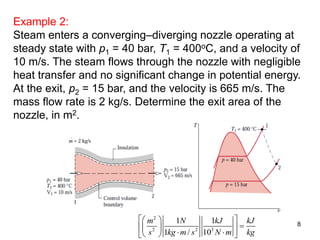
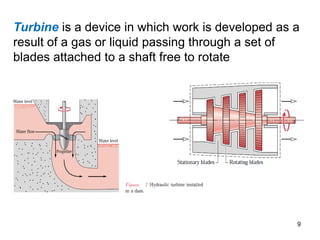
This document provides an overview of control volume analysis using energy concepts. It discusses key concepts like conservation of mass and energy for a control volume. It presents the steady state forms of the mass and energy rate balances. Examples are provided to demonstrate applying these concepts to devices like nozzles, turbines, compressors, heat exchangers, and throttling devices. The overall summary is that control volume analysis using energy concepts allows analyzing thermodynamic systems by applying conservation of mass and energy to a defined control volume.

1. Lesson 4:
CONTROL VOLUME ANALYSIS
USING ENERGY
1

2. 1. Conservation of Mass for a Control
Volume
2
time rate of change of time rate of flow time rate of flow
mass contained within of mass in across of mass out across
the control volume at time inlet at time exit at timet i t e t
    
         
        




cv
i e
i e
dm
m m
dt
  

3. 3
(one-dimensional flow)m AV
(one-dimensional flow)
AV
m
v

i e
i e
m m 
Steady-state Form

4. 4
Example 1:
A feedwater heater operating at steady state has two inlets
and one exit. At inlet 1, water vapor enters at p1 = 7 bar, T1
= 200oC with a mass flow rate of 40 kg/s. At inlet 2, liquid
water at p2 = 7 bar, T2 = 40oC enters through an area A2 =
25 cm2. Saturated liquid at 7 bar exits at 3 with a
volumetric flow rate of 0.06 m3/s. Determine the mass flow
rates at the exit and inlet 2, in kg/s, and the velocity at inlet
2, in m/s.

5. 2. Conservation of Energy for a Control Volume
5
2 2
2 2
cv i e
i i i e e e
dE V V
Q W m u gz m u gz
dt
   
          
   
2 2
2 2
cv i e
CV CV i i i e e e
i e
dE V V
Q W m h gz m h gz
dt
   
          
   
 
2 2
2 2
cv i e
CV CV i i i i i e e e e e
dE V V
Q W m u p v gz m u p v gz
dt
   
            
   
2 2
2 2
cv i e
CV CV i i i e e e
dE V V
Q W m h gz m h gz
dt
   
          
   

6. 3. Steady-state Forms of the Mass and Energy
Rate Balances
6
 
 
 
2 2
1 2
1 2 1 20
2
CV CV
V VQ W
h h g z z
m m

      
2 2
0
2 2
i e
CV CV i i i e e e
i e
V V
Q W m h gz m h gz
   
          
   
 
   
2 2
2 2
energy rate in energy rate out
i e
CV i i i CV e e e
i e
V V
Q m h gz W m h gz
   
         
   
 
 
 
 
2 2
1 2
1 2 1 20
2
CV CV
V V
Q W m h h g z z
 
       
  

7. 7
Nozzle is a flow passage of varying cross-sectional
area in which the velocity of a gas or liquid increases
in the direction of flow.
Diffuser, the gas or liquid decelerates in the direction
of flow
CVdm
dt
0
1 2
CV
m m
dE
dt
 
0
CV CVQ W 
2 20
1 2
1 1 1 2 2 2
2 2
V V
m h gz m h gz
   
        
   
 
 2 2
1 2
1 20
2
CV
V VQ
h h
m

   

8. 8
Example 2:
Steam enters a converging–diverging nozzle operating at
steady state with p1 = 40 bar, T1 = 400oC, and a velocity of
10 m/s. The steam flows through the nozzle with negligible
heat transfer and no significant change in potential energy.
At the exit, p2 = 15 bar, and the velocity is 665 m/s. The
mass flow rate is 2 kg/s. Determine the exit area of the
nozzle, in m2.
2
2 2 3
1 1
1 / 10
m N kJ kJ
s kg m s N m kg
  
  
   

9. 9
Turbine is a device in which work is developed as a
result of a gas or liquid passing through a set of
blades attached to a shaft free to rotate

10. Steam Turbine: Old & New
10

11. 11
Example 3:
Steam enters a turbine operating at steady state with a
mass flow rate of 4600 kg/h. The turbine develops a power
output of 1000 kW. At the inlet, the pressure is 60 bar, the
temperature is 400oC, and the velocity is 10 m/s. At the
exit, the pressure is 0.1 bar, the quality is 0.9 (90%), and
the velocity is 50 m/s. Calculate the rate of heat transfer
between the turbine and surroundings, in kW.

12. 12
Compressors are
devices in which
work is done on a
gas passing
through them in
order to raise the
pressure.
Pumps, the work
input is used to
change the state of
a liquid passing
through.

13. http://www.sulzerpumps.com/
Compressor and Pump
13

14. 14
Example 4:
Air enters a compressor operating at steady state at a
pressure of 1 bar, a temperature of 290 K, and a velocity of 6
m/s through an inlet with an area of 0.1 m2. At the exit, the
pressure is 7 bar, the temperature is 450 K, and the velocity
is 2 m/s. Heat transfer from the compressor to its
surroundings occurs at a rate of 180 kJ/min. Employing the
ideal gas model, calculate the power input to the
compressor, in kW.

15. 15
Heat Exchangers

16. 16
Example 5: Steam enters the condenser of a vapor power plant at
0.1 bar with a quality of 0.95 and condensate exits at 0.1 bar and
45oC. Cooling water enters the condenser in a separate stream as a
liquid at 20oC and exits as a liquid at 35oC with no change in
pressure. Heat transfer from the outside of the condenser and
changes in the kinetic and potential energies of the flowing streams
can be ignored. For steady-state operation, determine:
(a) the ratio of the mass flow rate of the cooling water to the
mass flow rate of the condensing stream.
(b) the rate of energy transfer from the condensing steam to
the cooling water, in kJ per kg of steam passing through the
condenser

17. 17
Throttling Devices: A significant reduction in pressure
can be achieved simply by introducing a restriction into
a line through which a gas or liquid flows.
1 20
0 CV CV
m m
Q W
 
 
2 20
1 2
1 1 1 2 2 2
2 2
V V
m h gz m h gz
   
        
   
2 2
1 2
1 2
2 2
V V
h h  
1 2h h

18. 18
Example 6:
A supply line carries a two-phase liquid–vapor mixture of steam
at 300 lbf/in.2. A small fraction of the flow in the line is diverted
through a throttling calorimeter and exhausted to the
atmosphere at 14.7 lbf/in.2. The temperature of the exhaust
steam is measured as 250oF. Determine the quality of the
steam in the supply line.

19. 19
System Integration
Simple vapor power plant