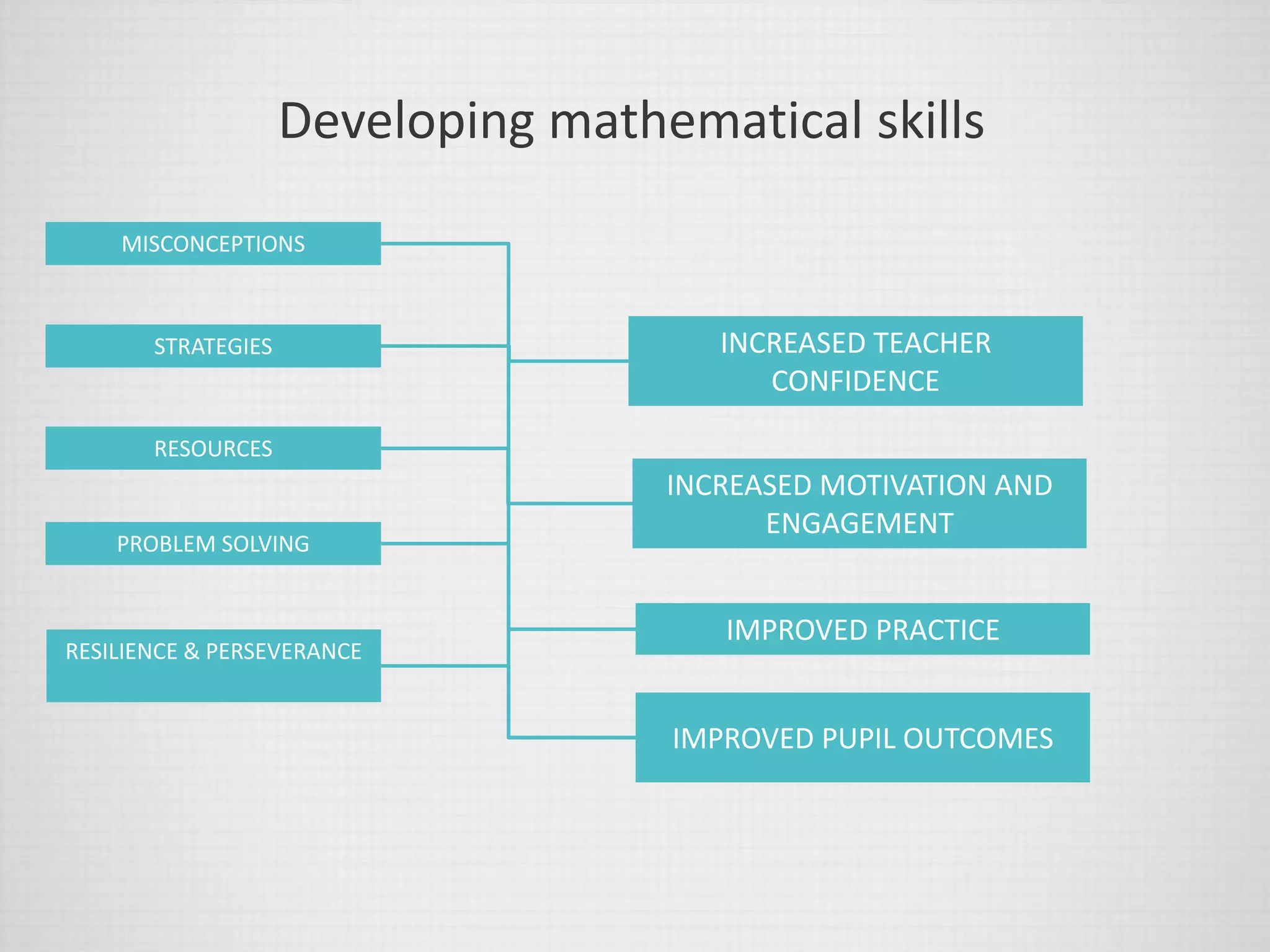
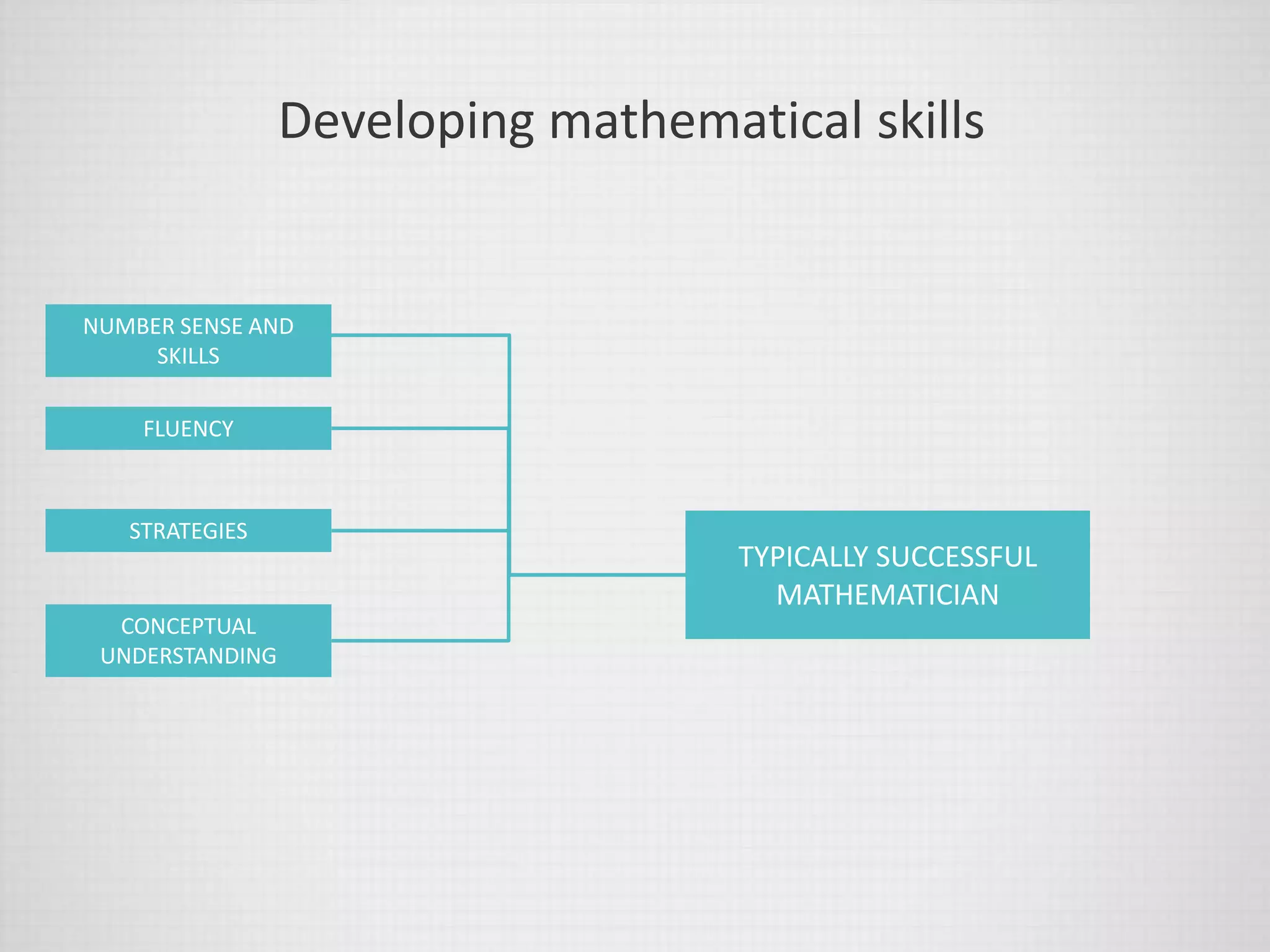
The document discusses developing primary teachers' math skills through professional development programs. It addresses the concept of number sense, which refers to a well-organized conceptual understanding of numbers that allows one to solve problems beyond basic algorithms. Examples are provided for dot arrangements and personal numbers to illustrate number sense strategies. Arithmetic proficiency is defined as achieving fluency through calculation with understanding. The benefits of improved teacher math skills are outlined as developing students' number sense, fluency, conceptual understanding, problem solving and engagement. Examples are given for teaching subtraction and extending students. The importance of understanding over procedural fluency alone is emphasized.