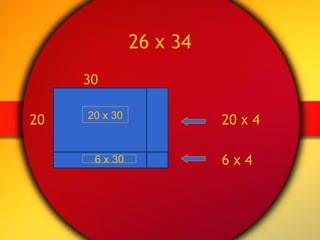
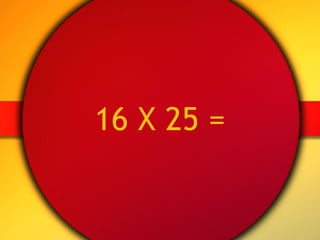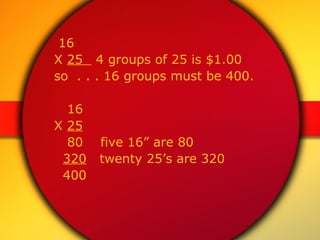Today's agenda includes a math lesson covering personal strategies for addition, subtraction, multiplication, and division. The schedule also includes a nutrition break, looking at virtual manipulatives and resources, lunch, and an assessment period. The document discusses teaching math concepts conceptually rather than procedurally and the importance of understanding operations rather than just memorizing computations. It provides examples of story problems and strategies adults use to solve math problems informally in everyday life.

2. Today’s Agenda 8:30 - 10:00 Personal Strategies Addition - Subtraction - Multiplication - Division 10:00 - 10:30 Nutrition Break SHSS Look at Resources 10:30 - 11:30 Virtual Manipulatives 11:30 - 1:00 Lunch 1:00 - ? Assessment

3. "Mathematics, as a body of knowledge, can be lost. But numeracy is the set of proficiencies that, once gained, are forever with you.” Dave Van Bergeyk

5. Young Mathematicians at Work

6. If learning doesn’t happen, there has been no teaching. The actions of learning and teaching are inseparable. - Catherine Twomey Fosnot

7. Procedural versus Conceptual?

8. Ma and Pa Kettle

9. “ When children are given trivial word problems they often just ask themselves which operation is called for. Truly problematic contexts engage children in a way that keeps them grounded. They attempt to model the situation mathematically as a way to make sense of it. They notice patterns, raise conjectures, and then defend them to one another.” – Young Mathematicians at Work

10. The Sub Question

11. 17 submarine sandwiches - 22 students. How much for each?

12. Which group got the better deal? What would have been fair?

13. Math Congress A “math congress” is a time when the whole class gathers and children present and discuss their strategies and solutions with one another.

14. "Mathematics is not a spectator sport!"

16. What’s at Stake? “ The ability to think mathematically will have to become something taken for granted as much as the ability to read a newspaper is at present. Such a change will seem fantastic to some people. But, so would universal literacy have seemed absurd a few centuries ago.” --W.W. Sawyer

17. Operations is a comparatively new addition to curriculum documents. There is a difference between understanding operations and computation.

18. How do these textbook problems not help students develop their understanding of operations? Addition Brenda has 11 toy horses and 12 toy cows. How many does she have all together? Andy coloured in 12 pages of his book on Monday and 18 pages on Tuesday. How many pages did he colour in altogether? Jean’s cat is 8 years older than her friend’s cat. If her friend’s cat is 11, how old is Jean’s cat?

19. We do students a disservice when we teach them to choose an operation by looking for “key” words.

20. Cookie Problem Kathy ate 6 cookies and Kim ate 7 cookies. How many cookies did the two girls eat?

21. Students need to interpret the situation (not just the words in the problem) and then decide which operation is the most appropriate. Begin with small easily visualized quantities.

22. Eventually students should solve a problem by first deciding on the operation and then using a computation.

23. Students should learn to write a number sentence that matches how they actually solve the problem even though this may produce a non - standard number sentence.

24. We had 8 hamsters but some escaped. Now we have 5 hamsters. How many hamsters escaped?

25. Result Unknown Change Unknown Start Unknown Addition Which do you think would be easiest to write? Keeping the same premise, write an addition problem for each of these situations.

26. People do calculations using a vast variety of informal methods, most of which are not written down in textbooks or explained by teachers to students, but which are actual methods most numerate adults employ for the calculations they encounter in everyday life.

27. How does this turn into equivalency? A calculator is handy for this. An understanding of part/part/whole is essential.

28. Subtraction? Result Unknown Change Unknown Start Unknown Can you write problems for each of these types of subtraction questions?

29. -secret # p 43 -focus on operations p 47

30. Personal Strategies

31. People do calculations using a vast variety of informal methods, most of which are not written down in textbooks or explained by teachers to students, but which are actual methods most numerate adults employ for the calculations they encounter in everyday life.

33. Informal Methods? Working from left to right is perfectly acceptable if the student is able to keep track. (Front End Approach)

34. Temporarily adding or subtracting numbers. . . 673 + 99 673 + 100 then take 1 away.

35. Breaking a number into Appropriate parts. 307 + 424 300 + 1 + 6 + 424

36. 16 X 25 =

37. 16 X 25 4 groups of 25 is $1.00 so . . . 16 groups must be 400. 16 X 25 80 five 16” are 80 320 twenty 25’s are 320 400

38. Addition

39. The key to understanding the process of adding two or more numbers is an understanding of the principle of place value. (Ten of those can be exchanged for one of these.)

40. Explore The Science Centre has a special show on the science of toys. The show has been on for 36 days. It will be on for another 48 days. How many days is that altogether. Use mental math to find out. Early grade 3 explore.

42. Algorithm? The algorithm is great! The algorithm is fast! But . . . . . Not until the student understands the concept. Watch your use of vocabulary!

43. 297 + 314

44. Watch the equals sign It means “is the same as”. Most children think that it means the answer is coming up.

45. Gina has 25 stamps. She has 11 more Canadian stamps than foreign stamps. How many foreign stamps does Gina have? Early Grade 5 Explores

46. So . . . How do we teach subtraction of multi digit numbers?

47. 345 - 96 =

48. Subtraction of multi digit numbers is straightforward when each digit in the first number is larger than each digit in the second number. 678 - 235

49. The trouble begins when . . . 345 - 96 Never say 5 take away 6 - You can’t do that . . . Let’s meet decomposition.

50. How does subtraction by decomposition work? A sound grasp of place value and some good manipulatives is in order. -demo using manips or coins -Use the words compose and decompose, not “borrow”.

51. 1700 - 586

52. Misconceptions and gaps. When students are struggling with addition or subtraction . . . . Not in place will be skip counting and place value.

53. Multiplication and Division What are they?

54. Multiplication is useful when we: • repeat equal quantities • use rates (4 shirts - 3 pairs of pants -how many outfits) • make ratio comparisons or changes (4 marbles for every child - 6 children) (Sam has 4 beads and Becky has 12 -How many more times) • make arrays and combinations • make scales (shopping -scales)

55. Potato Soup (Serves 8) 8 small potatoes 1L of water 4 chicken stock cubes 50 ml of butter 250 ml of cream What is needed to make soup for 16? What is needed to make soup for 12?

56. Our Job? Our job is to take students from being additive thinkers to multiplicative thinkers. Many students enter high school as additive thinkers. What are there struggles in elementary school?

57. In High School . . . Essentials . . . Drop out . . . Work hard get a “C”.

58. The new math streams are all rigorous. Apprenticeship and Workplace Foundations Pre Calculus

59. Multiplicative Changing the #’s in a problem will reveal lack of multiplicative thinking. Grapes cost 1.20 per Kilogram. How much for 4 Kilograms? How much for .3 Kilograms?

60. The Distributive Law 24 X 67 = (20 + 4) X (60 + 7) = 20 x 60 + 20 x 7 + 4 x 60 + 4 x 7 =

61. Try these two questions using the distributive law. 56 x 78 = 45 x 92 =

62. What is multiplication? Arrays? Rectangles? 26 x 34 =

63. 26 x 34 30 20 20 x 4 6 x 4 20 x 30 6 x 30

64. Using the .5 cm paper try: 72 x 45 = 86 x 13 =

65. Division The topic teachers most often leave for the next year’s teacher.

66. Dividing numbers is useful when we: Share a group or quantity into a given number of portions Share or group a quantity into portions of a given size Need the inverse of multiplication

67. Hannah had 18 cm of ribbon. She cut the ribbon into 6 cm pieces. How many people could have a piece of ribbon? Partition problem - you know how many parts. Hannah had 18 cm of ribbon. If 6 people equally shared the ribbon how long would the pieces of ribbon be? Quotation problem - you know the quota (how many in the group.

68. Game Did You Know Page 81 -you can use division or multiplication

69. Broken Keys The division key is broken on your calculator. How can you still use the calculator to discover 210 divided by 7? Broken subtraction key? Discover 65 subtract 47.

70. Game - Concentration Make cards such as 2 + 2 + 2 and the concentration match 3 x 2. 4 + 4 + 4 + 4 and the concentration match 4 x 4.

71. Game - Pass the # Any number including decimals and common fractions may be written on the top of a piece of paper. The paper is passed around the class. Each student writes an alternative form of the number. Try to circulate the paper without a repeat.

72. What is long division? Long division is the standard algorithm used when dividing a three digit number by a two digit number.

73. Short division is the standard algorithm often used for dividing by a single digit number. Students do not need to know how to divided by three digit numbers and greater. Use a calculator!

74. Have you ever heard about Friendly Division? Let’s see I can demonstrate or do I need to call my daughter?

75. Just the Facts Please Strategies - Strategies - Strategies Strategies only work if students have the number sense on which to build - otherwise strategies are just “ tricks”.

76. Drill? The very fact that so many students in grades 4, 5, 6, and beyond do not know their math facts . . . should be proof that drill is not effective for many students.

77. Madison, Wisconsin, Longitudinal Study 4: strategies, facts 3: counting on 2: counting all 1: incorrect Strategy use across grades 1-3

78. Assessment

79. GAMES Secret Number - page 43

80. Every classroom should have: A number line (not hung too high) Hundreds Charts Place Value Chart

81. http://www.mathplayground.com/math_manipulatives.html http://standards.nctm.org/document/eexamples/index.htm

82. Quotes to Ponder The Universe is a grand book that cannot be read until one first learns to comprehend the language and become familiar with the characters in which it is composed. It is written in the language of mathematics. – Galileo

83. Do not be troubled by your difficulties with Mathematics, I can assure you mine are much greater. - Albert Einstein

84. Music is the pleasure the human soul experiences from counting without being aware that it is counting. - Gottfried Leibniz

85. "42.7% of all statistics are made up on the spot." -- Steven Wright

86. "A man is like a fraction whose numerator Is what he is and whose denominator is what he thinks of himself. The larger the denominator, the smaller the fraction.” -- Tolstoy

87. "Five out of four people have trouble with fractions." -- Steven Wright

88. And my favourite …

89. "Math class is tough.” -- Talking Barbie Doll (1992)

90. Continued Readings Continued Readings Burns, Marilyn (1998) Facing an American Phobia Ma, Liping (1999) Knowing and Teaching Elementary Mathematics Schuster, Lainie & Canavan Anderson, Nancy Good Questions for Math Teaching : Why Ask Them and What to Ask Stigler, James W., and James Hiebert. (1999) The Teaching Gap: Best Ideas from the World’s Teachers for Improving Education in the Classroom.

91. Tobias, Sheila (1994) Overcoming Math Anxiety Anything by John Van de Walle or Marylin Burns SAUNDRY, C. AND NOVAKOWSKI, J.2005. Intermediate Investigations to Inspire Grades 4 - 8 TUMANOV, V.2002. Jayden’s Rescue (Scholastic)

92. http://www.mathplayground.com/math_manipulatives.html http://standards.nctm.org/document/eexamples/index.htm

93. www.slideshare.net