The document discusses the implementation of the Bellman-Ford algorithm for finding the shortest path in a network, detailing its operation at the network layer and its ability to handle negative edge weights. It outlines how the algorithm iteratively updates routing information to determine the minimum distance from a source node to all other nodes and includes sample Java code for its implementation. The document also provides example outputs demonstrating the algorithm's functionality, including handling cases with negative edge cycles.

1. Computer Network Laboratory-BCS502
Department of CSE - Data Science
Program 6: Develop a program to find the shortest path between vertices
using the Bellman-Ford and path vector routing algorithm

3. Bellman-Ford algorithm
 Bellman-Ford algorithm is used to find shortest path (minimum
distance) from one node to all the other nodes in a given network.
 It operates at network layer
 It is also called as Distance vector algorithm/Ford Fulkerson algorithm.
 It maintains a table which gives two pieces of information i.e next hop
and total cost.
 Bellman-Ford is capable of handling graphs that contain negative edge
weights, so it is more versatile.

4. How a Network is Represented
Network
Graph
Representation

5. How Bellman Ford's algorithm works
 One node is identified as the source node and shortest path from source to all
the other nodes is computed.
 Routing information at node is maintained in the form of a Routing table with
next hop and total cost details.
 Every node send its routing table to all its neighbors whenever its link table
changes. The Algorithm converges when there are no more updates.

6. • Initially all nodes, other than the source node 6, are at infinite
cost(distance) to node 6. Node 6 informs its neighbors it is at distance 0
from itself.
• Iteration 1:- Node 3 finds that it is connected to node 6 with cost of 1. Node
5 finds it is connected to node 6 at a cost of 2. nodes 3 and 5 update their
entries and inform their neighbors.
• Iteration 2:- Node1 finds it can reach node 6, via node 3 with cost 3. Node
2 finds it can reach node 6, via node 5 with cost 6. Node 4 finds it has paths
via nodes 3and 5, with costs 3 and 7 respectively. Node 4 selects the path via
node 3. Nodes 1, 2, and 4 update their entries and inform their neighbors.
• Iteration 3:- Node 2 finds that it can reach node 6 via node 4 with distance
4. Node 2 changes its entry to (4,4) and informs its neighbors.
• Iteration 4:- Nodes 1 and 5 process the new entry from node 2 but do not
find any new shortest paths. The algorithm has converged.

7. 1 3
5
6
2
4
Iteratio
n
Node
1
Node
2
Node
3
Node
4
Node
5
(6,0
)
(-1,
∞)
(-1,
∞)
(-1,
∞)
(-1,
∞)
(-1,
∞)
Initia
l
(-1,
∞)
(6, 1) (-1,
∞)
(6, 2)
(-1,
∞)
1
(5,6) (6,1) (3,3) (6,2)
(3,3)
2
(4,4) (6,1) (3,3) (6,2)
(3,3)
3
(4,4) (6,1) (3,3) (6,2)
(3,3)
4
Computation of the distances
source

8. Bellman-Ford algorithm
Consider computations for destination d
Step 1: Initialization
o Distance of node d to itself is zero: Dd=0
o Distance of other node i to d is infinite: Di=∞, for i≠d
o Send new distance vector to immediate neighbors across local link
Step 2: Updating(find minimum distance to destination through neighbors)
o For each i≠d,
o Di= min {Cij+Dj}, for all j≠i
j
 Repeat Step 2 until no more changes occur in the iteration. 0 3 2 5 999 999
3 0 999 1 4 999
2 999 0 2 999 1
5 1 2 0 3 999
999 4 999 3 0 2
999 999 1 999 2 0
Input to the algorithm is passed in
the form of weighted matrix. Matrix
for the given graph is

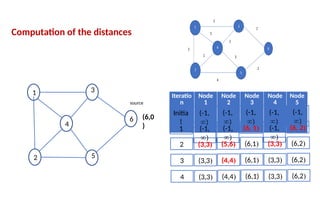
9. Program 6: Write a program to find the shortest path between vertices
using bellman-ford algorithm.
import java.util.Scanner;
public class BellmanFord
{
private int D[];
private int n;
public static final int MAX_VALUE = 999;
public BellmanFord(int n) Constructor of the class
{
this.n=n;
D = new int[n+1]; Creates an array D to hold the distance information
}
public void shortest(int d, int A[][])
{
for (int i=1;i<=n;i++)
D[i]=MAX_VALUE; Initially all n values in D is set to infinity which is 999

10. D[d] = 0; Distance from destination to itself is set to zero
for(int k=1;k<=n-1;k++)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(A[i][j]!=MAX_VALUE) for every node distance is updated in array D, if an
alternate path is available path through a neighbor
which is better than the current
if(D[j]>D[i]+A[i][j]) {
D[j] is the current distance value, D[i]+A[i][j] is the
D[j]=D[i]+A[i][j]; new path through neighbor i
}
}
}
}

11. for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(A[i][j]!=MAX_VALUE)
{
if(D[j]>D[i]+A[i][j]) The same condition which was tested in the previous loop is
checked, if it is true here the graph contains negative edges
{
System.out.println("The Graph contains negative egde cycle");
return;
}
}
}
}
for(int i=1;i<=n;i++)
{
System.out.println("Distance from " +i+ “ to destination " +d+ "is " + D[i]); Finally array D will
have the computed distance from all
} the vertices to the destination vertex
}

12. public static void main(String[ ] args)
{
int n=0,d;
Scanner sc = new Scanner(System.in);
System.out.println("Enter the number of vertices");
n = sc.nextInt();
int A[][] = new int[n+1][n+1];
System.out.println("Enter the Weighted matrix");
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
A[i][j]=sc.nextInt(); read the weighted matrix A
}
System.out.println("Enter the destination vertex");
d=sc.nextInt(); select the destination node
BellmanFord b = new BellmanFord(n); create an object of the class
b.shortest(d,A); Call the shortest function
sc.close();
}
}

13. OUTPUT 1
run:
Enter the number of vertices
6
Enter the Weighted matrix
0 3 2 5 999 999
3 0 999 1 4 999
2 999 0 2 999 1
5 1 2 0 3 999
999 4 999 3 0 2
999 999 1 999 2 0
Enter the destination vertex
6
Distance from 1 to destination 6 is 3
Distance from 2 to destination 6 is 4
Distance from 3 to destination 6 is 1
Distance from 4 to destination 6 is 3
Distance from 5 to destination 6 is 2
Distance from 6 to destination 6 is 0

14. OUTPUT 2
run:
Enter the number of vertices
6
Enter the Weighted matrix
0 -3 2 5 999 999
-3 0 999 1 4 999
2 999 0 2 999 1
5 1 2 0 3 999
999 4 999 3 0 2
999 999 1 999 2 0
Enter the destination vertex
6
The Graph contains negative edge cycle
BUILD SUCCESSFUL (total time: 1 minute 11
seconds)
-