Download as PDF, PPTX
Complex network-reading 7
- 2. 成長しないネットワークモデル 第6章では主にネットワークにエッジを持った ノードが逐次加入してくるようなモデルを考え た 例えばWWWにおいて新規にWebページが作成され 既存のページにリンクを貼ったり、貼られたりと いった関係を表している 本章ではネットワークのノードが固定されたモ デルを考える 例えば学校のクラス内の人間関係のネットワークが 相当する(転校などがなければ基本的にクラス内の ノードは固定されたものになる)
- 3. 本章で扱うモデルの仮定 ネットワークの枝の切り替えは考えない 例えばクラスの人間関係ネットワークでは新た に交友関係が生まれることも考えられるが、こ こではこれは考慮しない 理由としては解析がしやすいというのがある
- 4. 今日の話 7.1から7.3の3つのネットワークモデルにつ いて紹介する 7.4は微妙に6章の話が入ってるので次回
- 5. 7.1 コンフィグモデル 頂点数Nを固定する 𝑁−1 次数分布𝑃 = 𝑝 𝑘 𝑘=0 を考える 各ノードの次数を𝑃から発生させ、N個の次 数𝑘1 , … , 𝑘 𝑁 を得る 各頂点の次数が与えられた次数と一致する ようにネットワークを作成する
- 6. 次数からのネットワークの作成 例えばN=4のとき次数が(2,2,1,1)のネット ワークは下のようなものが例として挙げら れる
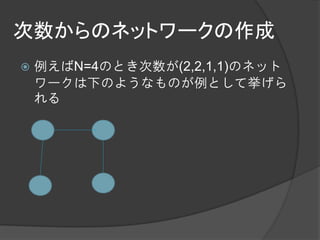
- 7. 次数からのネットワークの作成 与えられた次数からネットワークを作成す るにはHavel-Hakimiのアルゴリズムが利用 できる http://en.wikipedia.org/wiki/Degree_(graph_theor y) これは次数の大きいノードから次に次数が大き いノードに対して貪欲にエッジを貼っていくア ルゴリズムである このアルゴリズムにより与えられた次数を持つ ネットワークが存在する場合は必ず構成できる
- 8. コンフィグモデルの特徴 次数分布をべき則にすればスケールフリー ネットワークを構成できる ランダムグラフの拡張になっている 次数相関はない 次数分布を考慮した平均場近似があてはま る
- 9. コンフィグモデルの平均距離 𝑁 → ∞で< 𝑘 2 >が存在するとき 𝑁 log <𝑘> 𝐿 =1+ <𝑘 2 >−<𝑘> log <𝑘> また次数分布がスケールフリーで𝑝 𝑘 ∝ 𝑘 −𝛾 のとき 𝐿 = log log 𝑁 (2 < 𝛾 < 3) 𝐿 = log 𝑁 / log log 𝑁 (𝛾 = 3) 𝐿 = log 𝑁 (𝛾 > 3)
- 10. コンフィグモデルのクラスタ係数 ランダムグラフと同様に頂点𝑣の２つの隣接点𝑣 ′ , 𝑣′′を考 えた時に2頂点の間に枝が張られる確率がクラスタ係数に なる 今𝑣′の次数を𝑘′, 𝑣′′の次数を𝑘′′とすると𝑘 ′ − 1本の枝のう ′ 𝑘 ′′ −1 ちどれか一本が𝑣′′につながる確率は約(𝑘 −1) <𝑘>𝑁 𝑘′ 𝑝 𝑘′ また(2.7)式より𝑣′の次数が𝑘′である確率は , 𝑣′′の次 <𝑘> 𝑘 ′′ 𝑝 𝑘 ′′ 数が𝑘′′である確率は <𝑘> これを𝑘 ′ , 𝑘′′に渡って平均すると 2 <𝑘 2 >−<𝑘> 𝐶= <𝑘>3 𝑁
- 11. コンフィグモデルのクラスタ係数 <𝑘> 次数分布がポアソン分布の場合𝐶 = とな 𝑁 りランダムグラフの結果と一致する スケールフリーの場合はCはやや大きくなる が、𝑁 −1 の項があり小さいと思って良い
- 12. レギュラーランダムグラフ コンフィグモデルで各点の次数が必ず𝑘0 で あるようなものをレギュラーランダムグラ フと呼ぶ これはランダムグラフに見られるような次 数の散らばりがないため、次数が散らばる ことの影響を調べたい時に比較対象として 用いられる
- 13. 7.2 一般の次数分布を持つ木 コンフィグモデル同様に一般の次数分布を 持つ木を作成できる 一般化ランダムグラフと呼ばれることがあ るが、ランダムグラフの一般化にはなって いない 次数分布がべき則の場合はスケールフリー 木と呼ばれることもある
- 14. 作り方 次数分布{𝑝 0 , 𝑝 1 , … }を決める 孤立点は無いものとするので𝑝 0 = 0 頂点𝑣1 をおき、 𝑣1 の次数𝑘1 を確率𝑝(𝑘1 )で決 める 𝑣1 の頂点から𝑘1 本の枝をつなぎ、それぞれ の枝の先に新しい頂点をおく それぞれの頂点の先に(決められた次数-1)本 の枝をおき、再帰的に木を構成する
- 15. ゴルドンワトソン過程 個体の繁殖など表すモデルでゴルドンワト ソン過程があり、これは一般の次数を持つ 木とほぼ同じである 1. 1個体が何個体かの子を産んで死ぬ 2. 生まれた子は次世代の親となり、やはり 何個体か産んで死ぬ 3. 次の世代が子を産み、同様の過程を繰り 返す これからでる系譜図が木に対応する
- 16. 集団の発展 ゴルドンワトソン過程においての関心とし ては世代を経ていくうちに集団が生き残る かどうかである ∑ 𝑘 − 1 𝑝 𝑘 > 1となるときに限って集団は 生き残りうる ネットワークの話題に戻ると平均次数< 𝑘 > が2より大きければ一般の次数分布をもつ木 は無限に遠くまで広がりうる
- 17. 7.3 GohモデルとChung-Luモ デル Gohモデルの作り方は以下のようになる 1. 頂点数𝑁と平均次数< 𝑘 >を決める 2. 頂点𝑣 𝑖 に重み𝑤 𝑖 = 𝑖 −𝛼 (1 ≤ 𝑖 ≤ 𝑁)を割り当て る 3. 𝑁頂点の中から𝑤 𝑖 に比例する確率で頂点𝑣 𝑖 , 𝑣 𝑗 を選択する 4. 𝑣 𝑖 , 𝑣 𝑗 がまだ隣接していないなら２つをつなげ る 5. ステップ3,4を枝が合計< 𝑘 > 𝑁/2本になる まで繰り返す
- 18. Gohモデルの特徴 𝑣 𝑖 の次数𝑘 𝑖 はステップ3で𝑣 𝑖 が選ばれる確率 に比例し 𝑘 𝑖 ∝ 𝑝 𝑖 ∝ 𝑖 −𝛼 これと(2.1.3)より次数分布はべき則 1 𝑝 𝑘 ∝ 𝑘 −𝛾 , 𝛾 =1+ となる 𝛼 Lは小さく、Cも小さい また次数相関は負になる これはハブに枝が集中しやすいことからである
- 19. Chung-Luモデル Gohモデル同様に各頂点は𝑤 𝑖 をもち、𝑣 𝑖 , 𝑣 𝑗 𝑤𝑖 𝑤𝑗 を確率∑ でつなぐ 𝑙 𝑤𝑙 Gohモデルよりも数学的に解析しやすい 確率は1以下になると仮定する 𝑤𝑖 𝑤 𝑗 Gohモデルでは約 2 となっていた ∑𝑙 𝑤𝑙
- 20. Chung-LuモデルにおけるL コンフィグモデルと同様に次数がべき分布 のとき 𝐿 = log log 𝑁 (2 < 𝛾 < 3) 𝐿 = log 𝑁 / log log 𝑁 (𝛾 = 3) 𝐿 = log 𝑁 (𝛾 > 3)
- 21. 隣接行列の固有値 Chung-Luモデルにおける固有値の分布もべ き則に従うことが知られている 𝜌 𝜆 ∝ 𝜆−2𝛾−1 Gohモデルについても、レプリカ法という 手法によって同様の式が成り立つことが知 られている