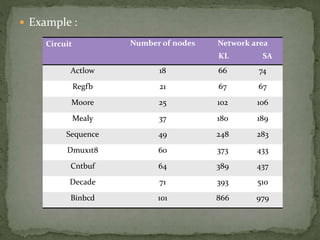
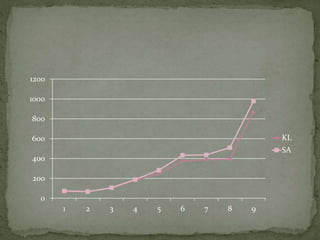
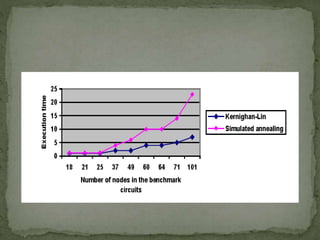
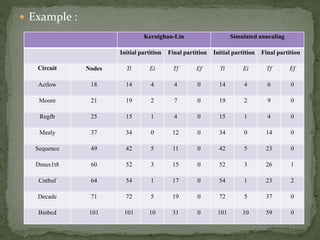
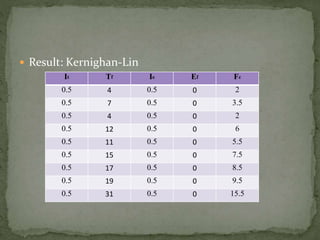
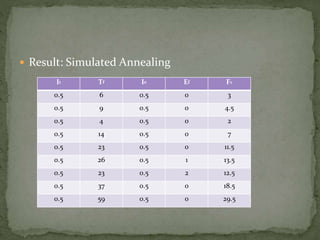
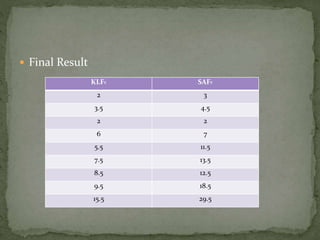
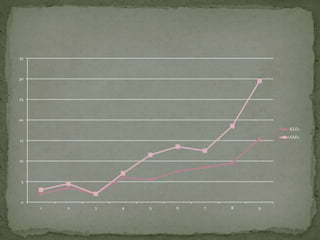
The document summarizes a study comparing the Kernighan-Lin (KL) and Simulated Annealing (SA) graph partitioning algorithms. The study evaluated the algorithms based on estimated network area, execution time, and cost function on various benchmark circuits. For smaller circuits, there was little difference between the algorithms. However, for larger circuits with more nodes, KL produced better results with lower execution times and cost function values compared to SA. The KL algorithm was found to produce the best overall results.

1. 02/11/2015

3.  Graph Partitioning is an important problem in area of
VLSI design.
 Partitioning is used to find strongly connected
components that can be placed together in order to
minimize the layout area and propagation delay.

4.  The bi-partitioning algorithm proposed by kernighan-
lin randomly starts with two subsets, and pair wise
swapping is iteratively applied on all pairs of nodes.
 Simulated Annealing is another method based on
iterative improvement. The objective function in SA is
analogous to physical system, and each move is
analogous to changes in energy of the system.

5.  The simulated annealing (SA) algorithm is a widely
used iterative technique for solving general
optimization problems. It is an adaptive heuristic and
belongs to the class of non-deterministic algorithms.
 Locates a good approximation to the global optimum
in a large search space.

6.  SA guarantees finding an optimal solution, generally
gives a “good” solution.
 Relatively easy to code, even for complex problems.

7.  We do a comparative study based on three criteria
--> Estimation of an network area of a graph.
--> The Execution Time.
--> The Cost Function.

8.  This is an estimation of the implementation area
obtained after the placement of the graph.
 Area is estimated by calculating the Manhattan
distance between each possible node in the graph.
 X=(X1, X2, …., Xn) and Y=(Y1, Y2, …., Yn)
d = ∑ |xi– yi|

9.  Example :
Circuit Number of nodes Network area
KL SA
Actlow 18 66 74
Regfb 21 67 67
Moore 25 102 106
Mealy 37 180 189
Sequence 49 248 283
Dmux1t8 60 373 433
Cntbuf 64 389 437
Decade 71 393 510
Binbcd 101 866 979

10. 0
200
400
600
800
1000
1200
1 2 3 4 5 6 7 8 9
KL
SA

11.  For a small number of nodes, the difference between
result is almost negligible, but when the number of
nodes increase, the difference becomes significant.
 The result suggest that the solution obtained by KL
algorithm are better then by SA algorithm.

12.  For a small number of nodes, there are no significant
differences between the results of two algorithms. But
for higher number of nodes, the execution time grows
for the SA algorithm

14.  Ti and Tf represents the initial cut size and the final
cut size. Ei and Ef represents the initial and the final
balance number, indicating the difference between the
number of connections in the two parts of the
partition.
 The cost function Fc is computed according to the
following formula:
Fc = It · Tf + Ie · Ef

15.  Example :
Kernighan-Lin Simulated annealing
Initial partition Final partition Initial partition Final partition
Circuit Nodes Ti Ei Tf Ef Ti Ei Tf Ef
Actlow 18 14 4 4 0 14 4 6 0
Moore 21 19 2 7 0 19 2 9 0
Regfb 25 15 1 4 0 15 1 4 0
Mealy 37 34 0 12 0 34 0 14 0
Sequence 49 42 5 11 0 42 5 23 0
Dmux1t8 60 52 3 15 0 52 3 26 1
Cntbuf 64 54 1 17 0 54 1 23 2
Decade 71 72 5 19 0 72 5 37 0
Binbcd 101 101 10 31 0 101 10 59 0

16.  where It indicates the relative importance of reducing
the cut size, and Ie indicates the relative importance of
balancing the number of connections. We used the
following values for It and Ie: It = 0.5, Ie = 0.5. This
means that both criteria have the same importance.
Notice that It + Ie = 1.

17.  Result: Kernighan-Lin
It Tf Ie Ef Fc
0.5 4 0.5 0 2
0.5 7 0.5 0 3.5
0.5 4 0.5 0 2
0.5 12 0.5 0 6
0.5 11 0.5 0 5.5
0.5 15 0.5 0 7.5
0.5 17 0.5 0 8.5
0.5 19 0.5 0 9.5
0.5 31 0.5 0 15.5

18.  Result: Simulated Annealing
It Tf Ie Ef Fc
0.5 6 0.5 0 3
0.5 9 0.5 0 4.5
0.5 4 0.5 0 2
0.5 14 0.5 0 7
0.5 23 0.5 0 11.5
0.5 26 0.5 1 13.5
0.5 23 0.5 2 12.5
0.5 37 0.5 0 18.5
0.5 59 0.5 0 29.5

19.  Final Result
KLFc SAFc
2 3
3.5 4.5
2 2
6 7
5.5 11.5
7.5 13.5
8.5 12.5
9.5 18.5
15.5 29.5

20. 0
5
10
15
20
25
30
35
1 2 3 4 5 6 7 8 9
KLFc
SAFc

21.  The results show that the KL algorithm produces the
best results when we consider the execution time and
the cost function. From the point of view of the
estimated network area, the differences are not
significant.

22.  Comparative Study of Circuit Partitioning Algorithms
by Zoltan Baruch, Octavian Creţ, Kalman Pusztai .