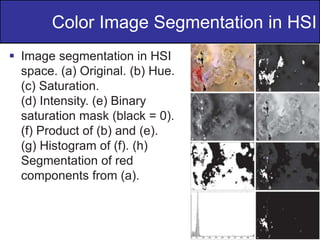
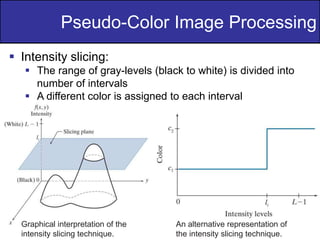
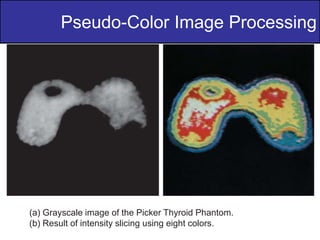
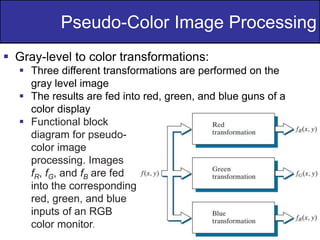
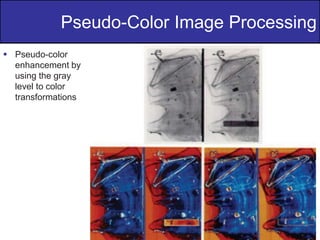
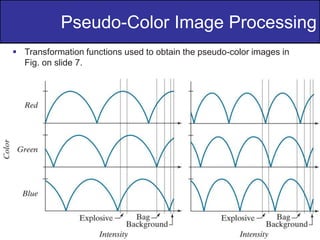
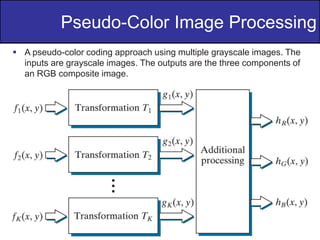
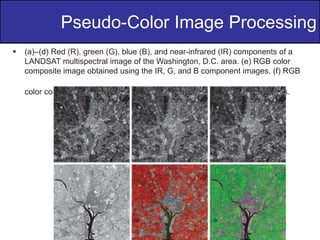
The document discusses various techniques in digital image processing, particularly focused on pseudo-color image processing, where colors are assigned to monochrome images for better visual distinction. Key methods include intensity slicing, gray-level to color transformations, and filtering approaches, which enable enhanced interpretation of data within grayscale images. Furthermore, it outlines color transformations, tonal corrections, histogram processing, and segmentation techniques, emphasizing their application in RGB and HSI color spaces for effective image analysis.





![16
of
36
Color Transformations
Color transformation can be represented by the
expression:
g(x,y)=T[f(x,y)]
f(x,y): input image
g(x,y): processed (output) image
T[*]: an operator on f defined over neighborhood
of (x,y).
The pixel values here are triplets or quartets (i.e
group of 3 or 4 values)](https://image.slidesharecdn.com/lecture-13-240608094752-c14af71b/85/Color-Image-Processing-Digital-Image-processing-16-320.jpg)