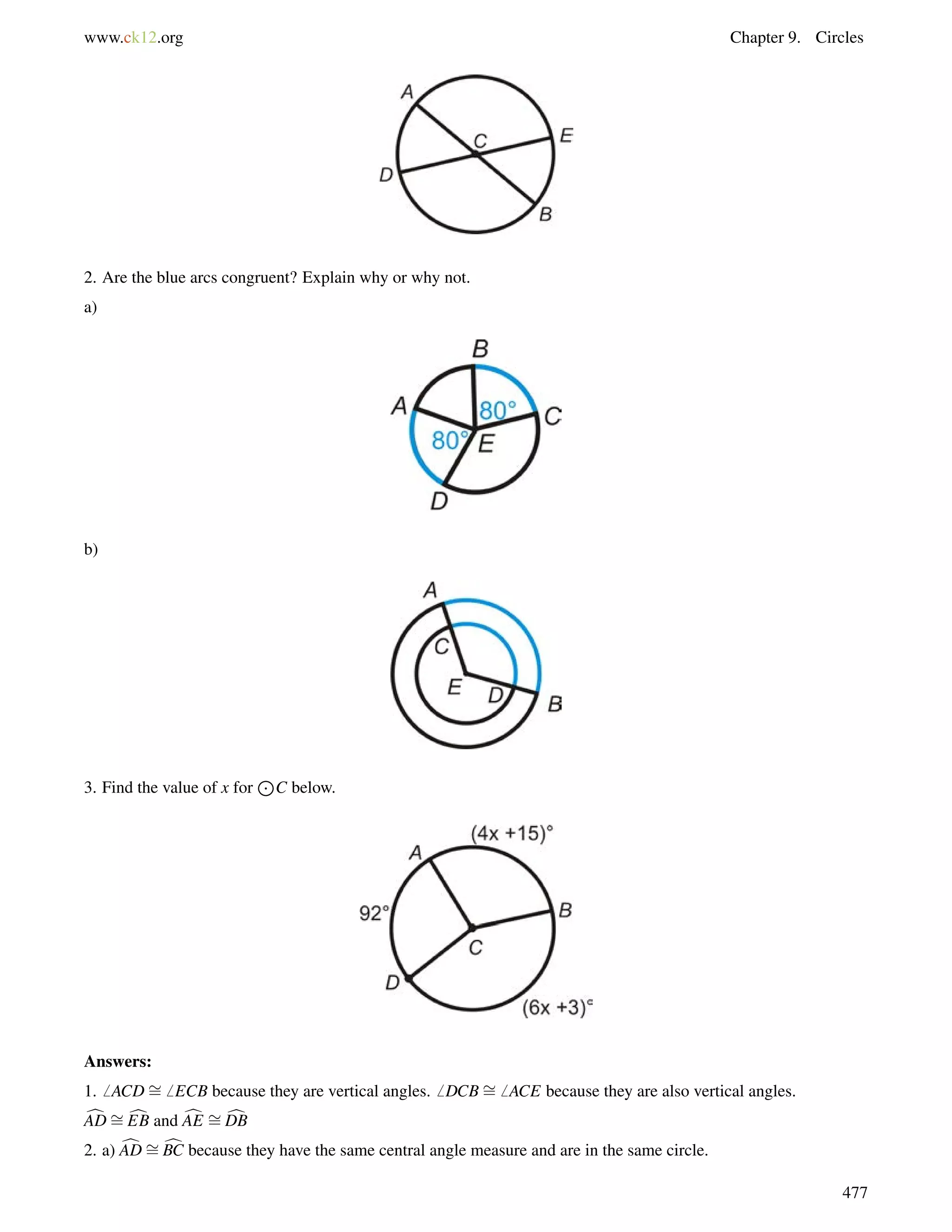
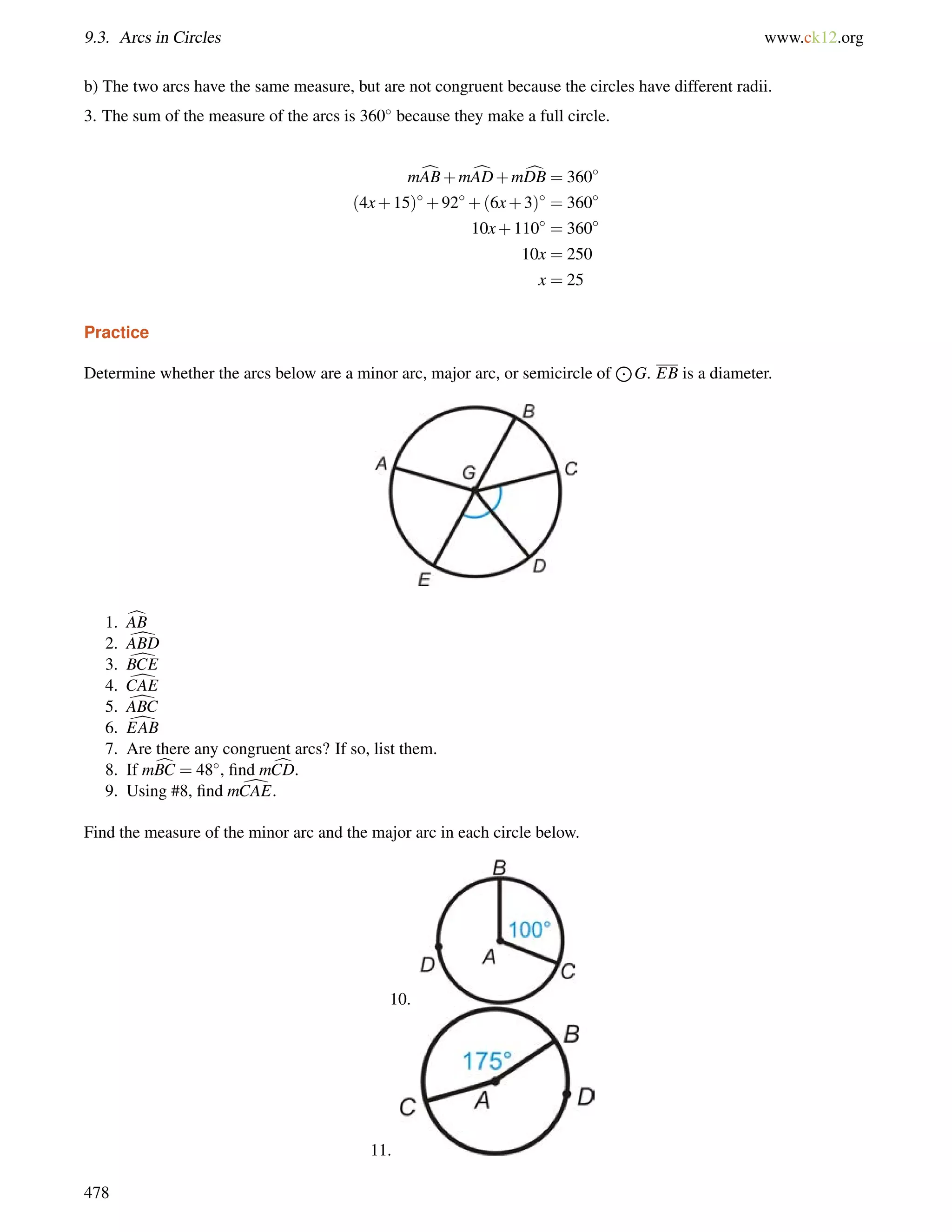
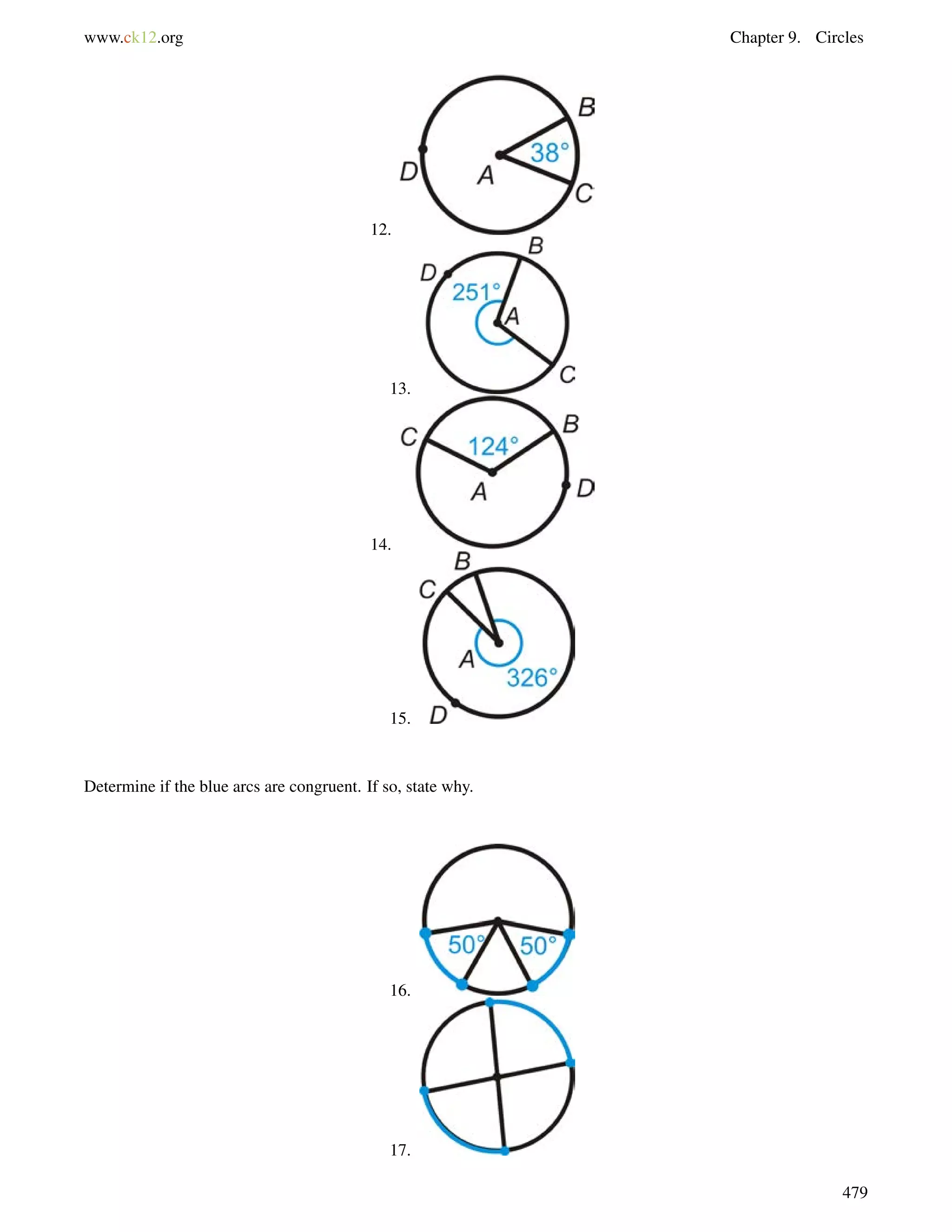
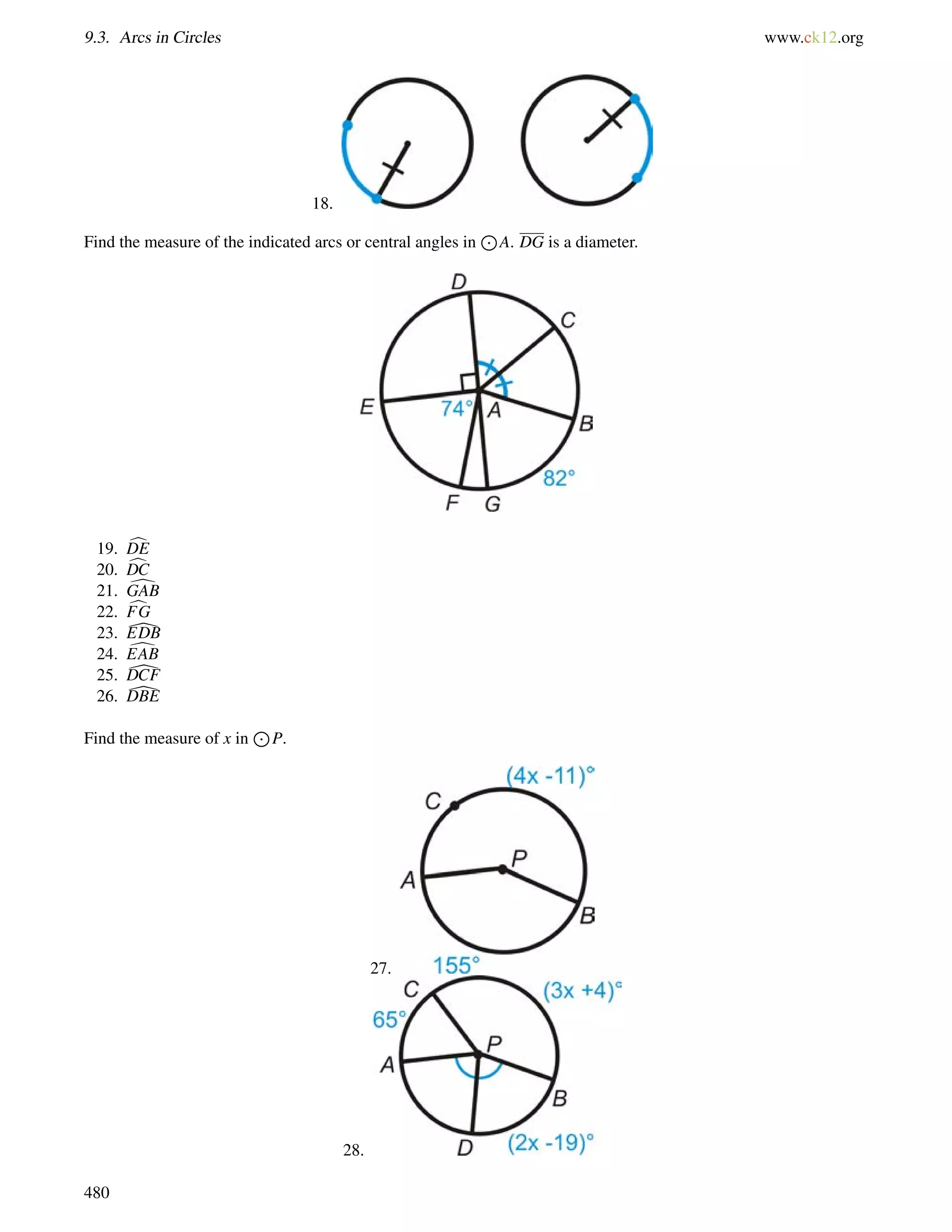
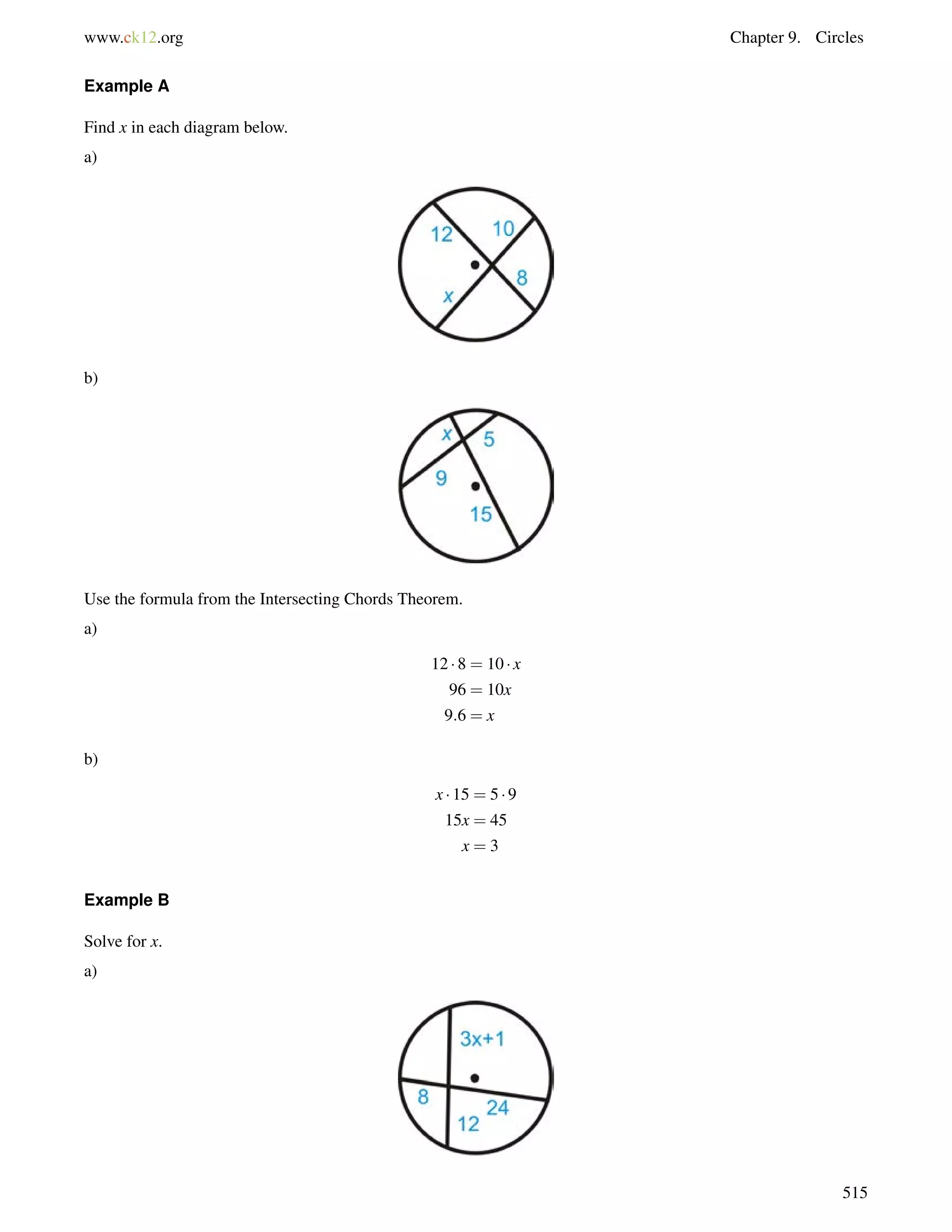
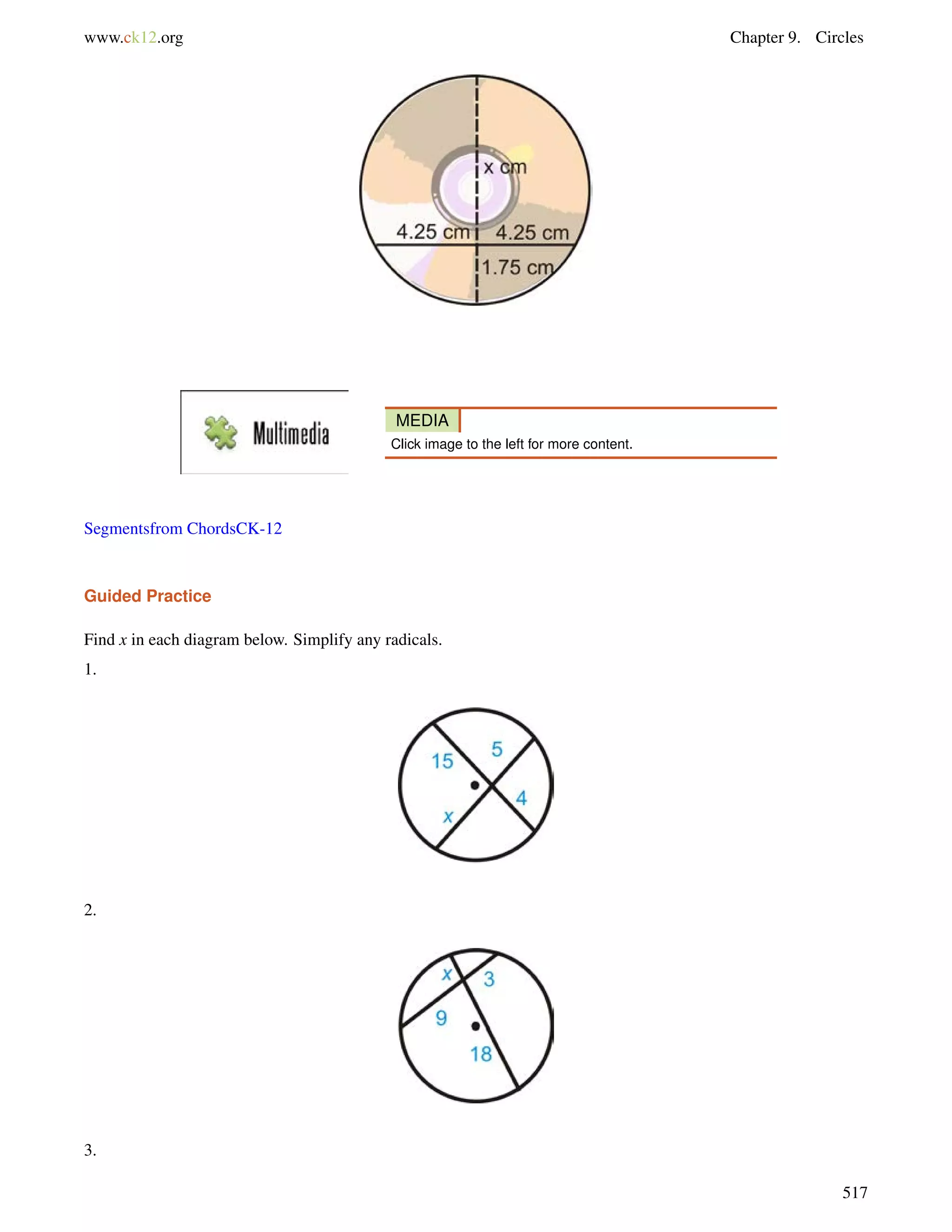
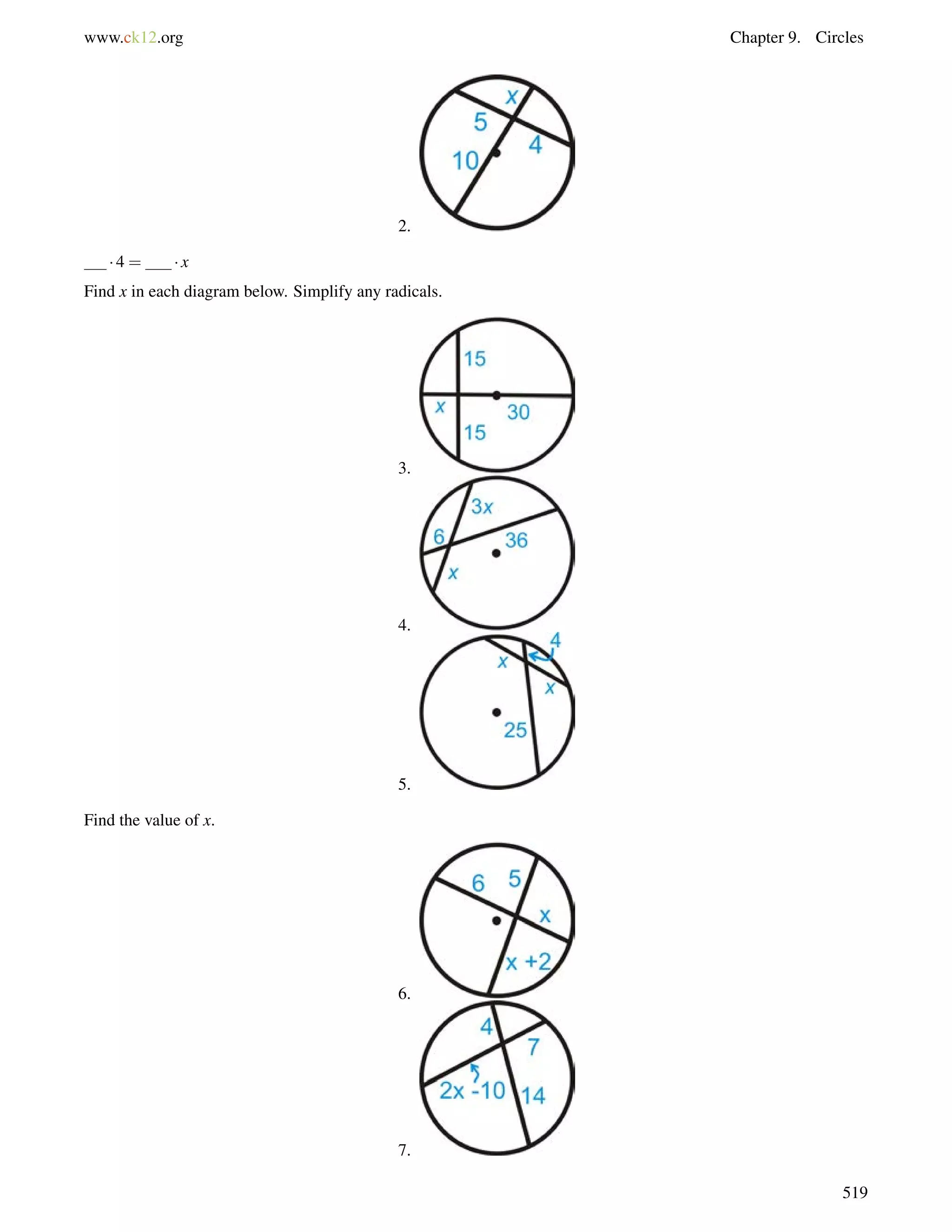
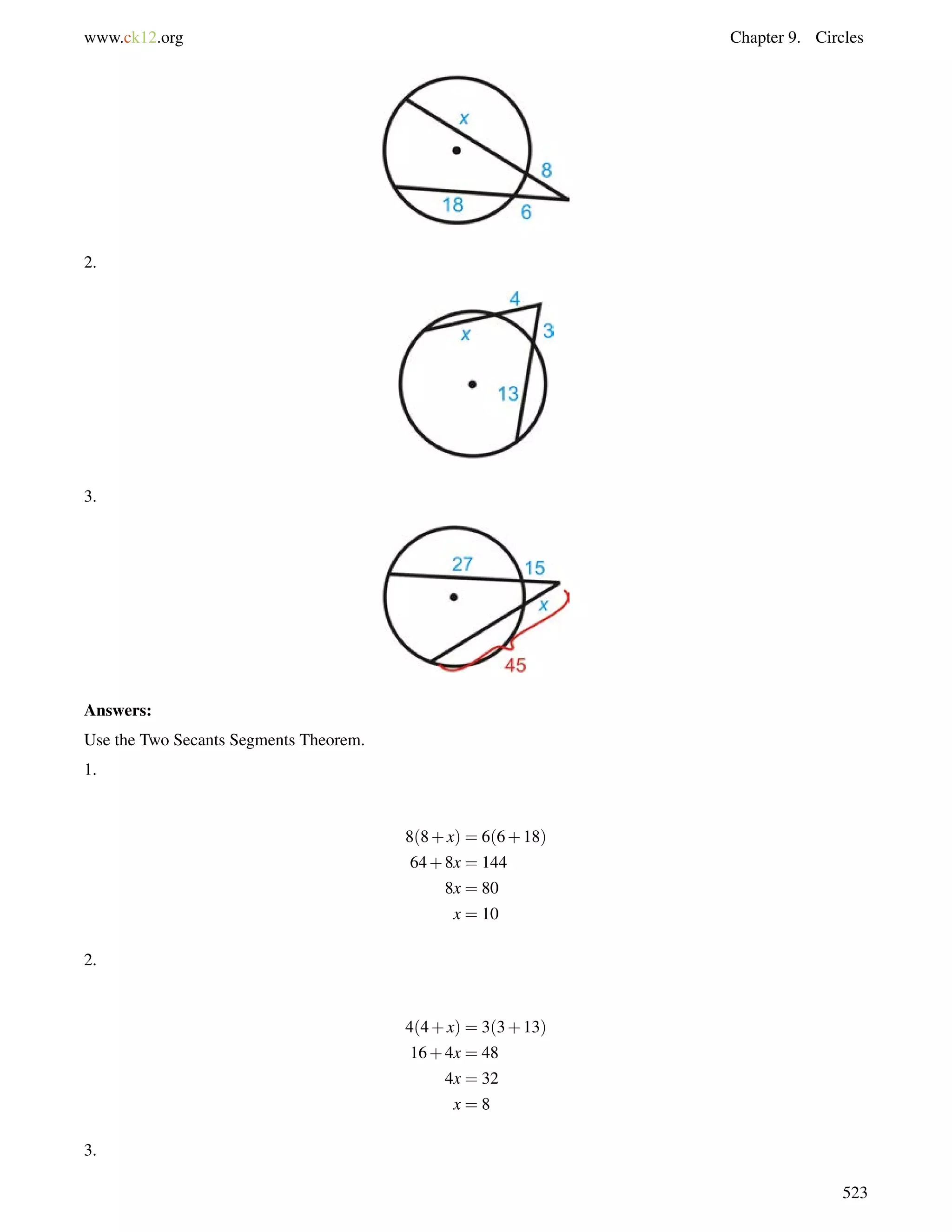
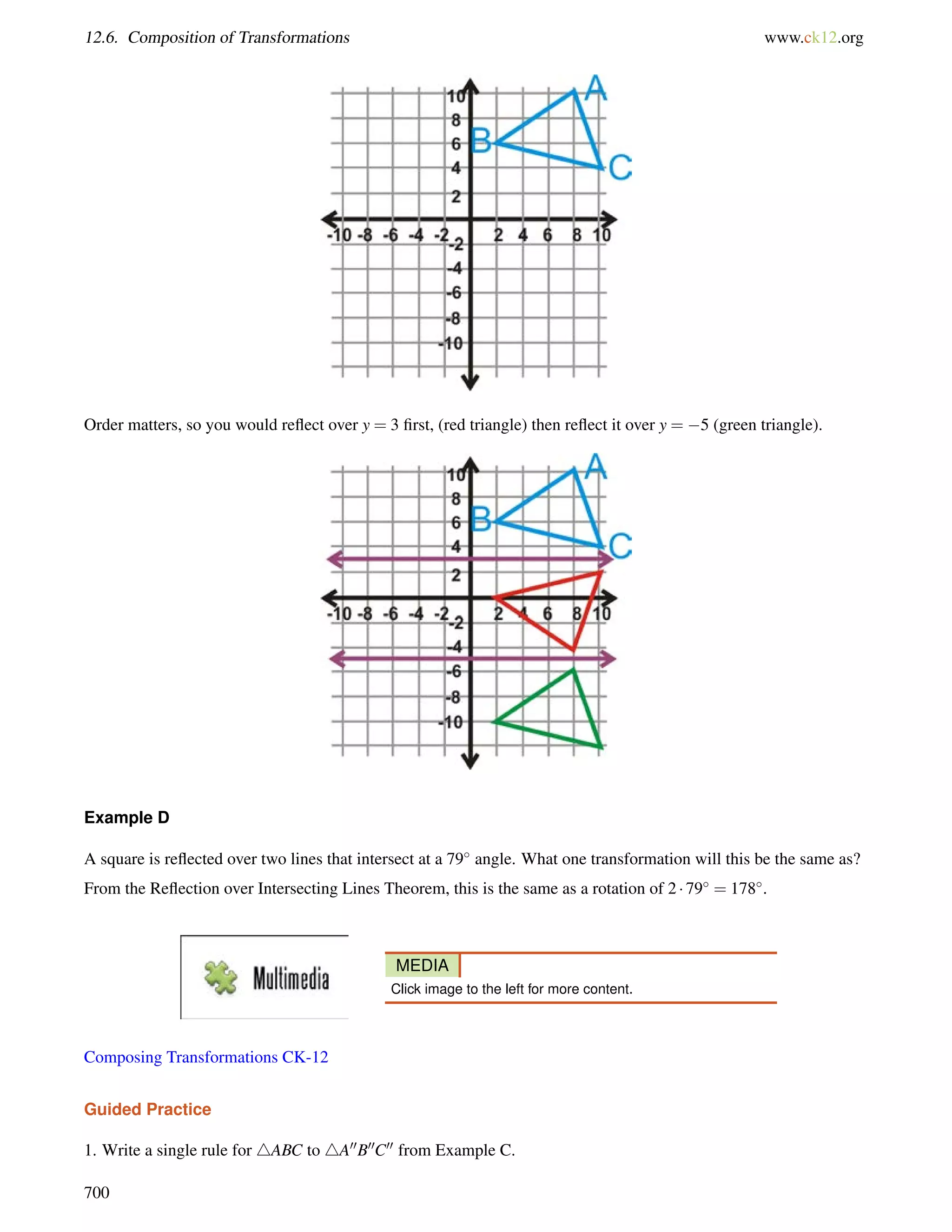
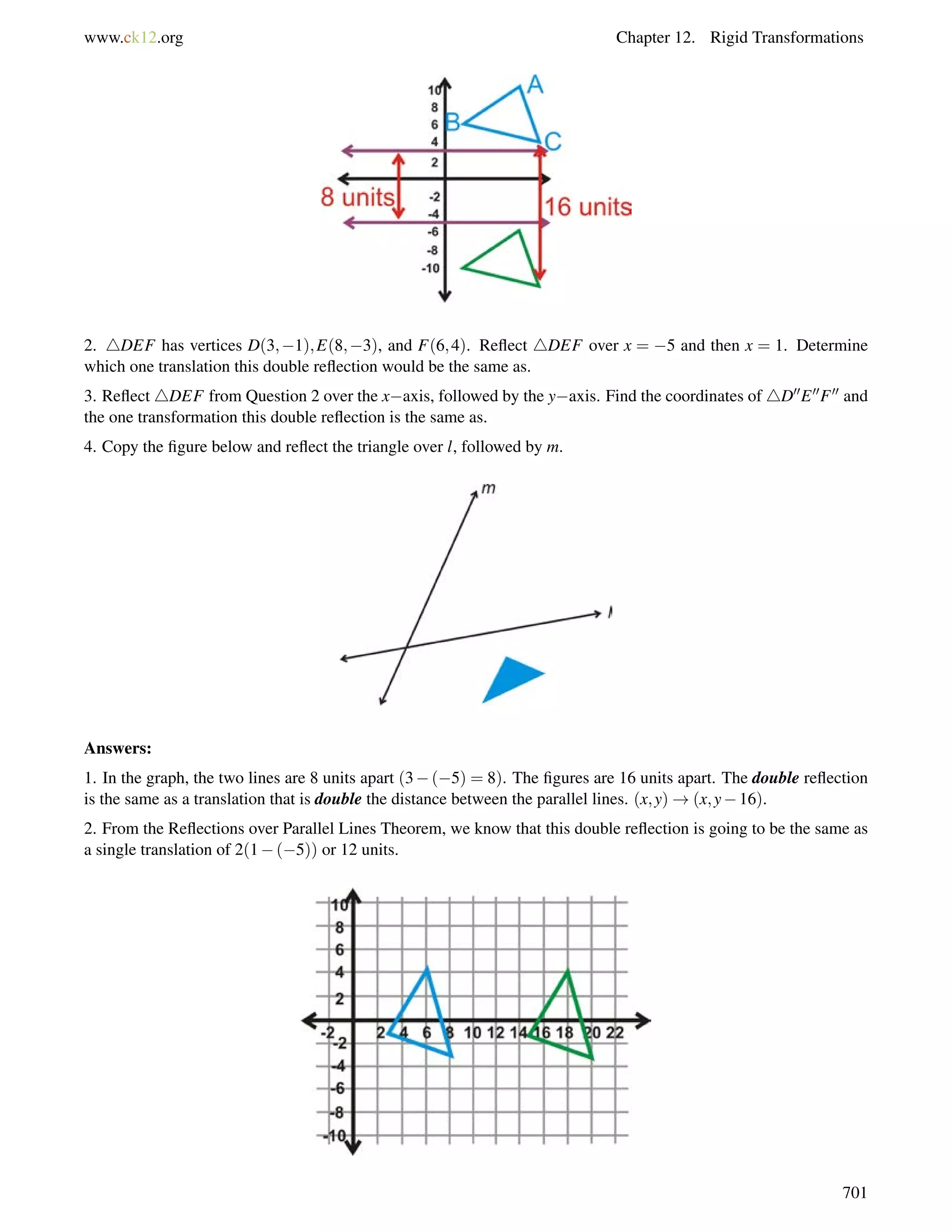
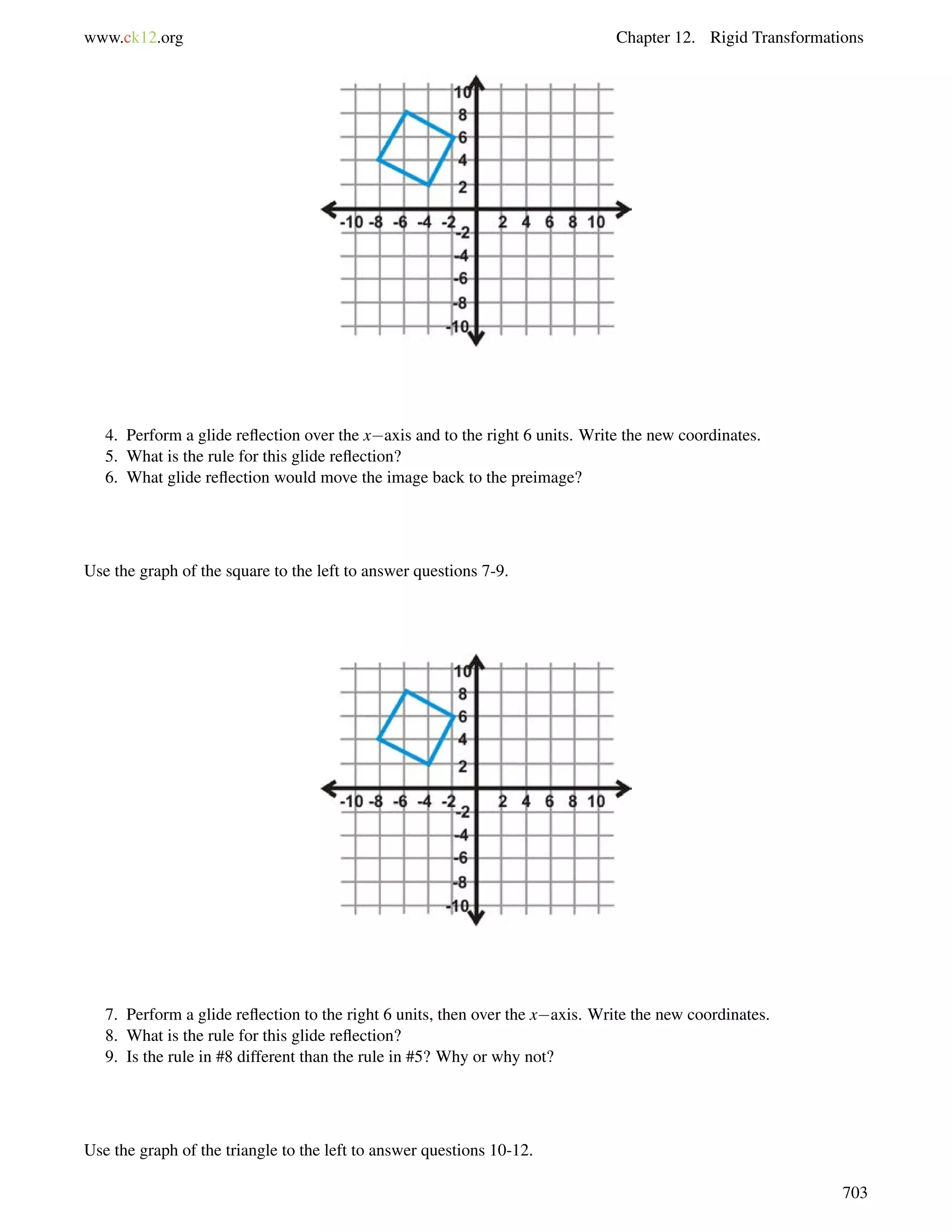
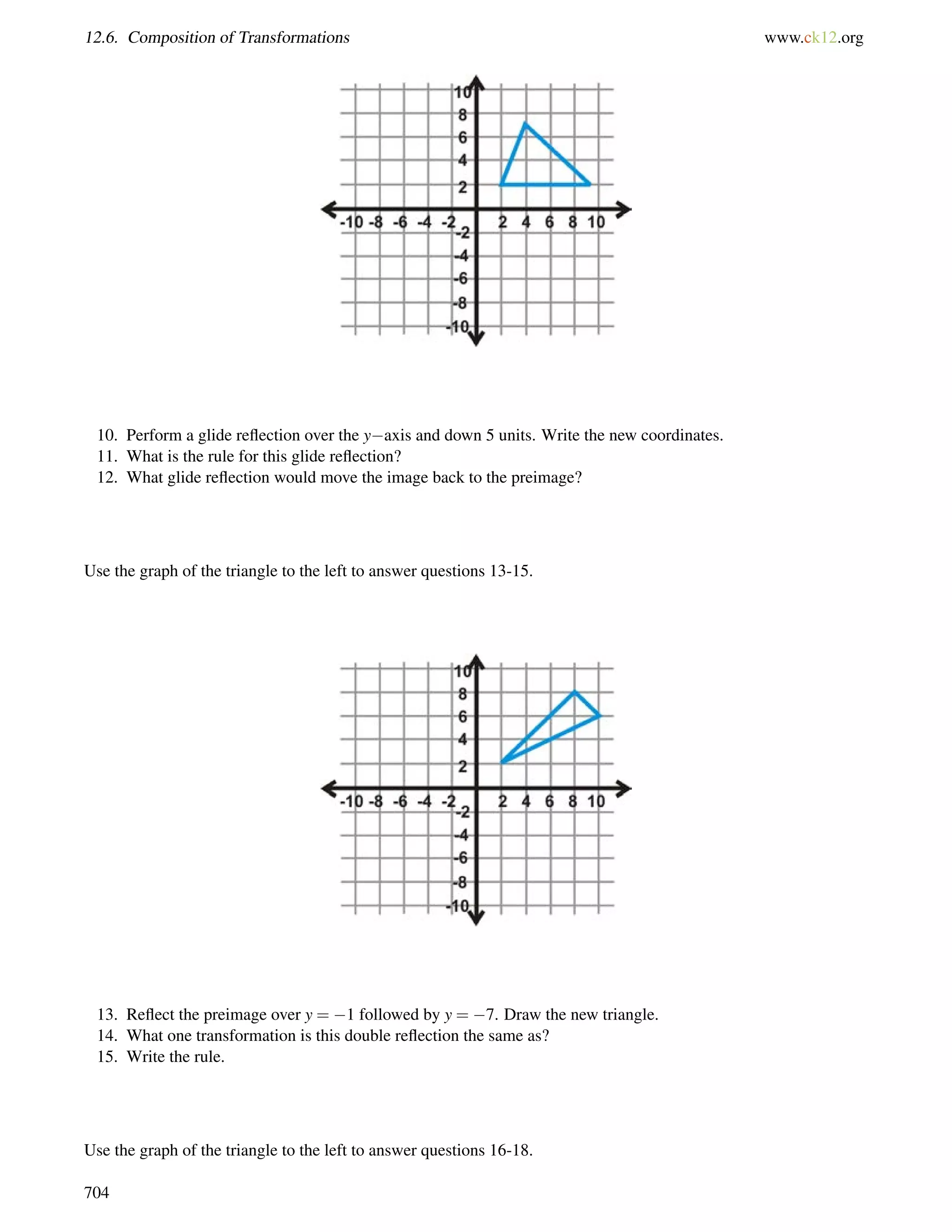
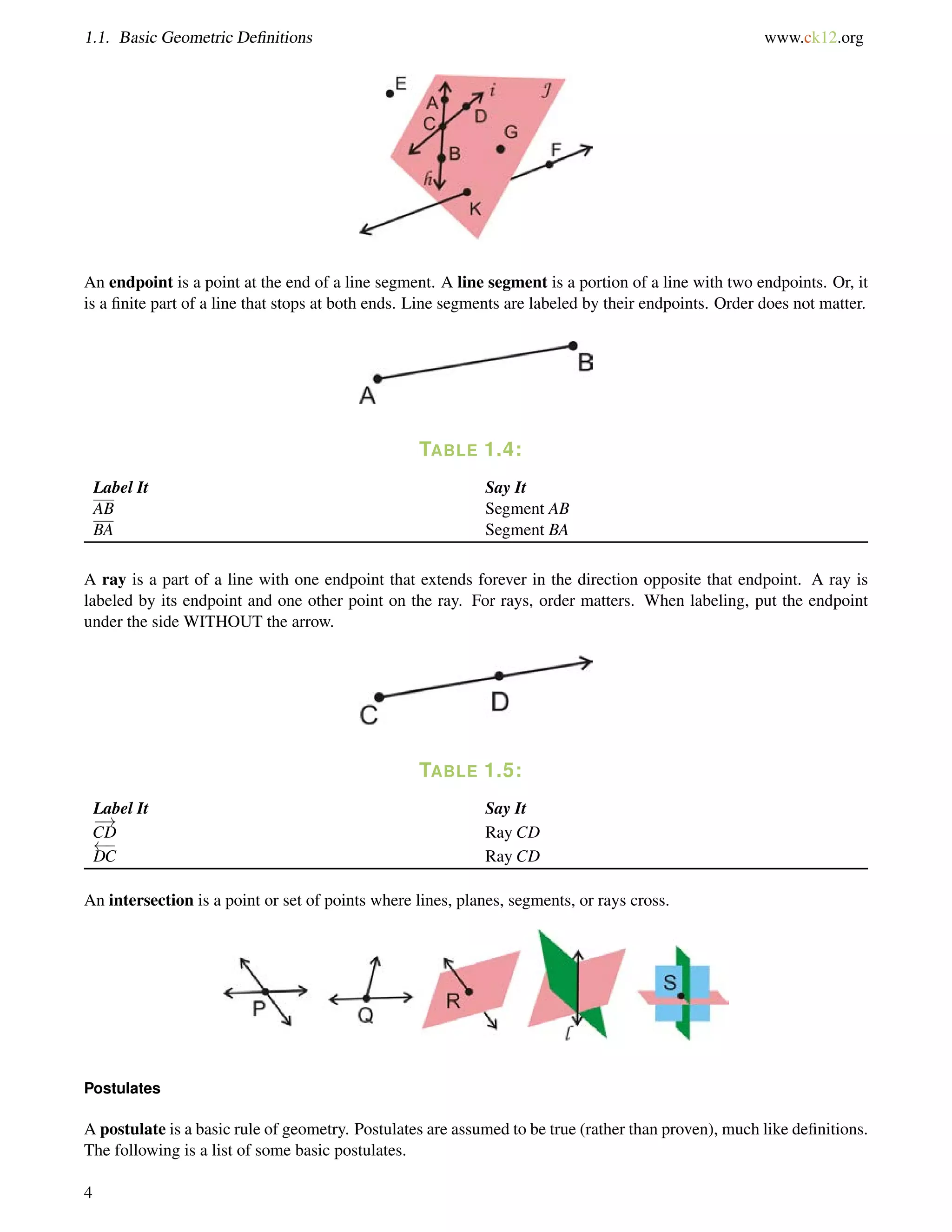
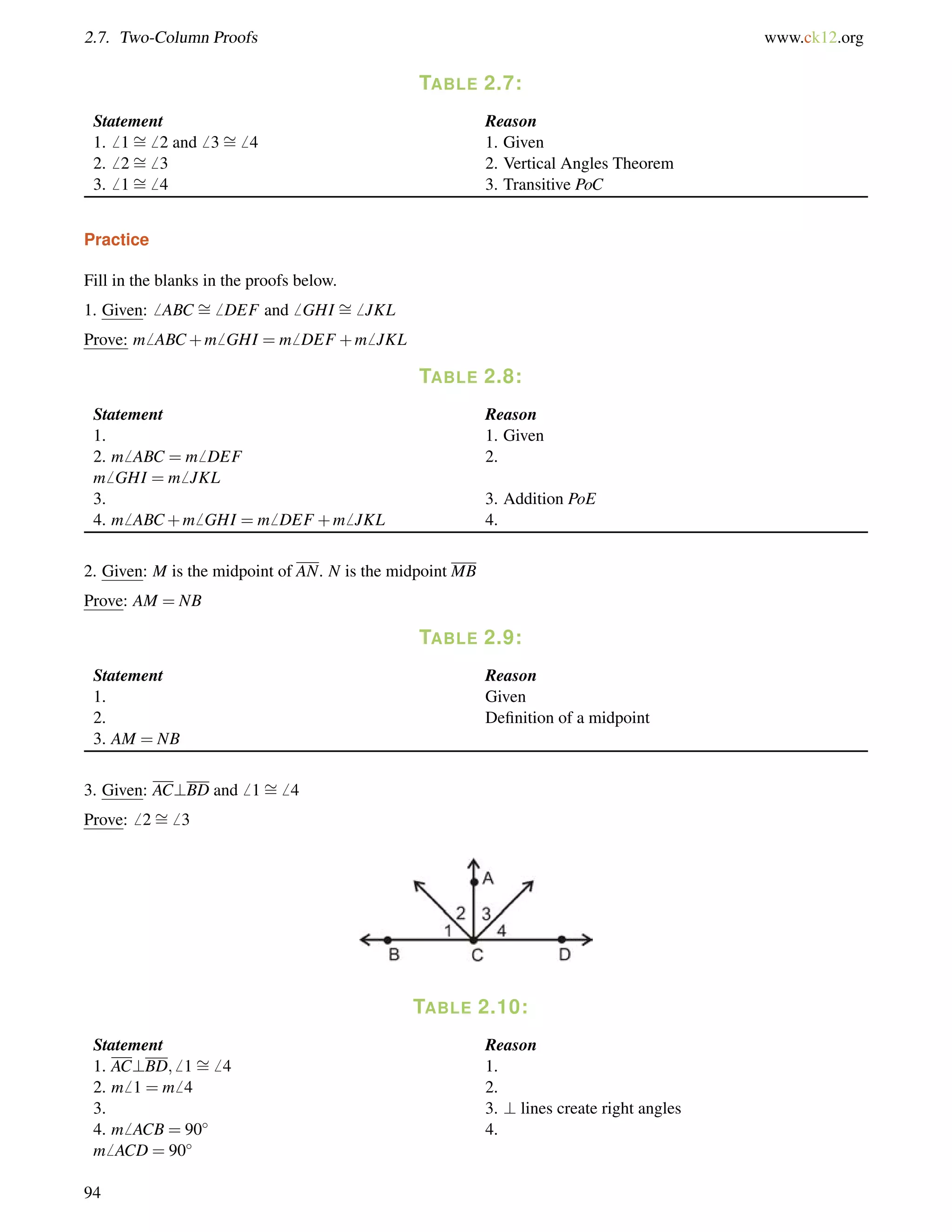
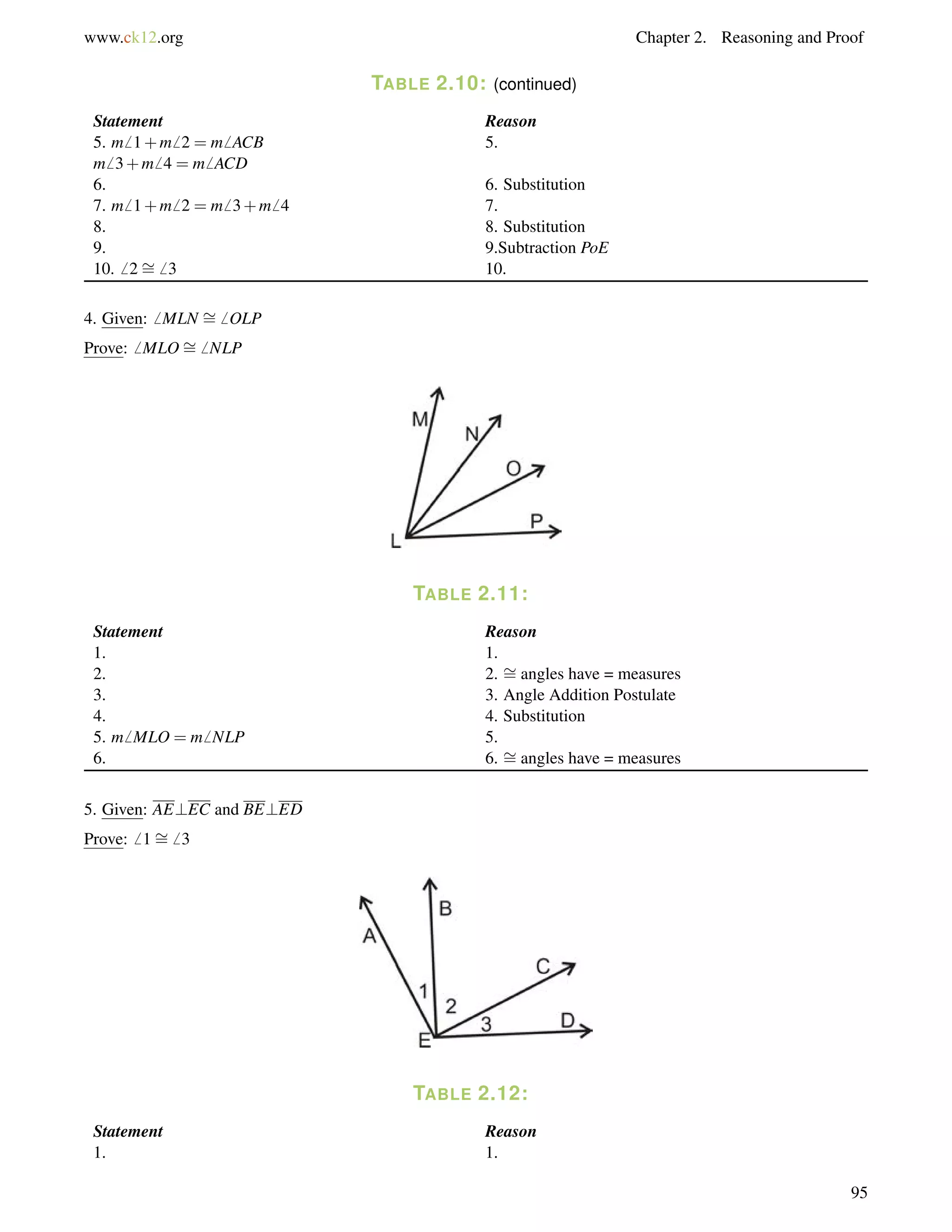
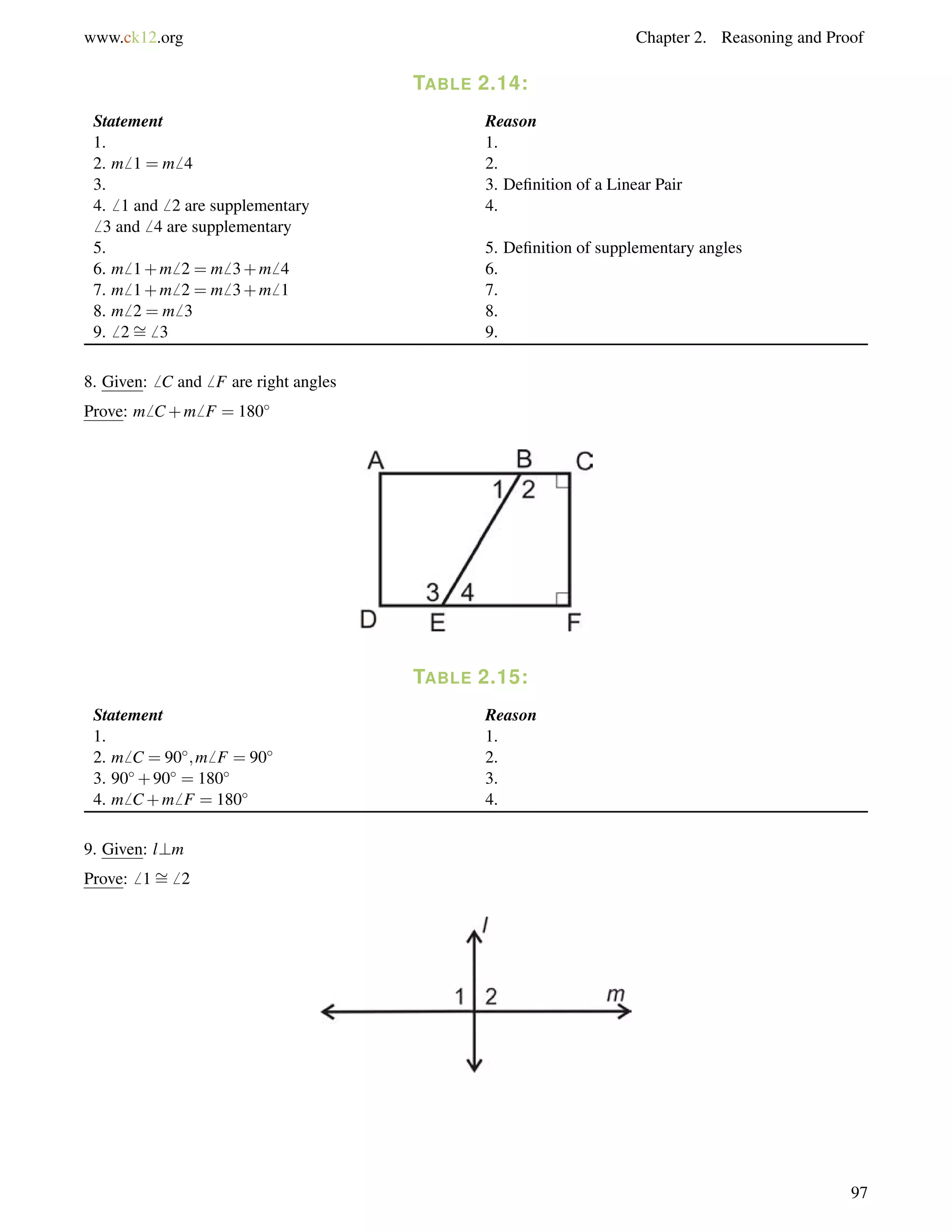
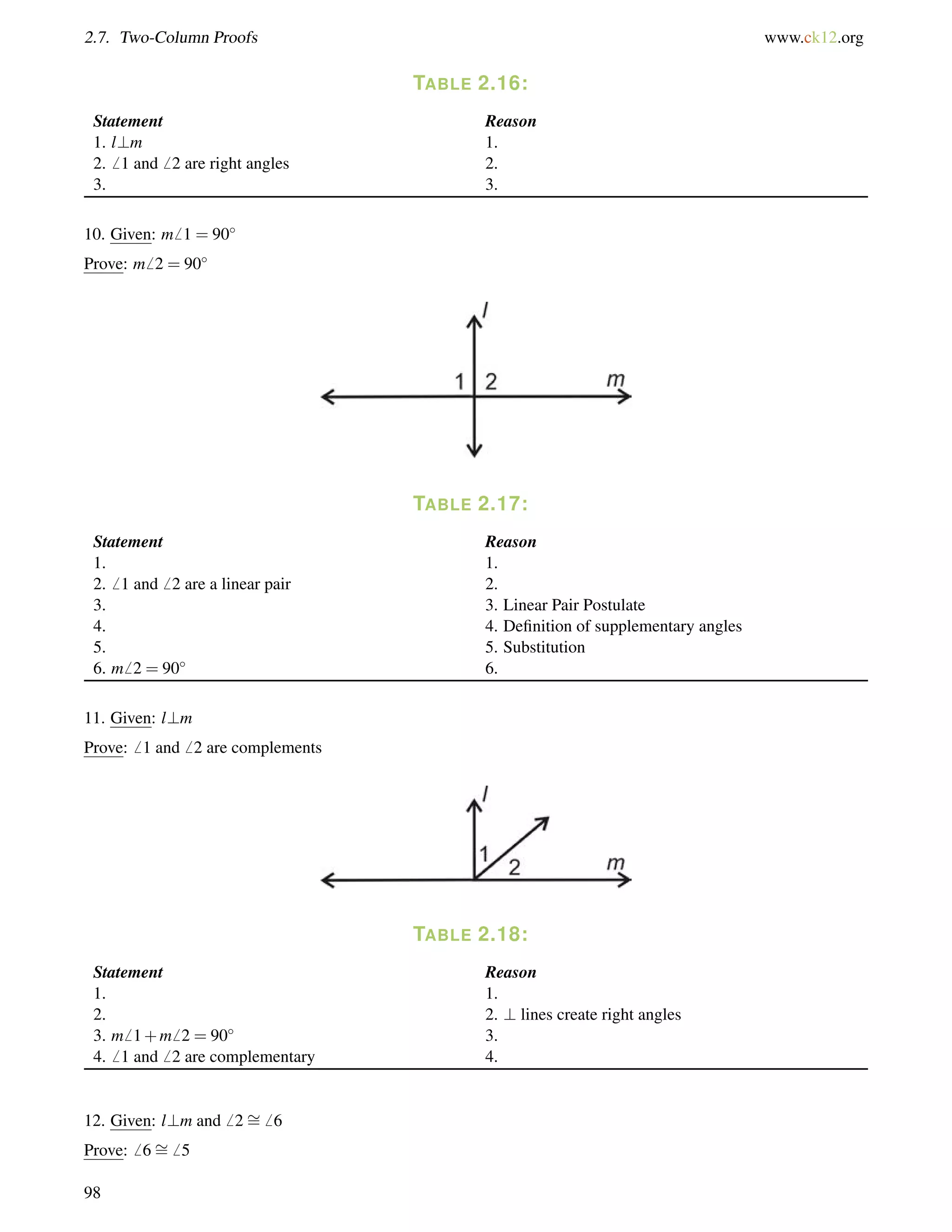
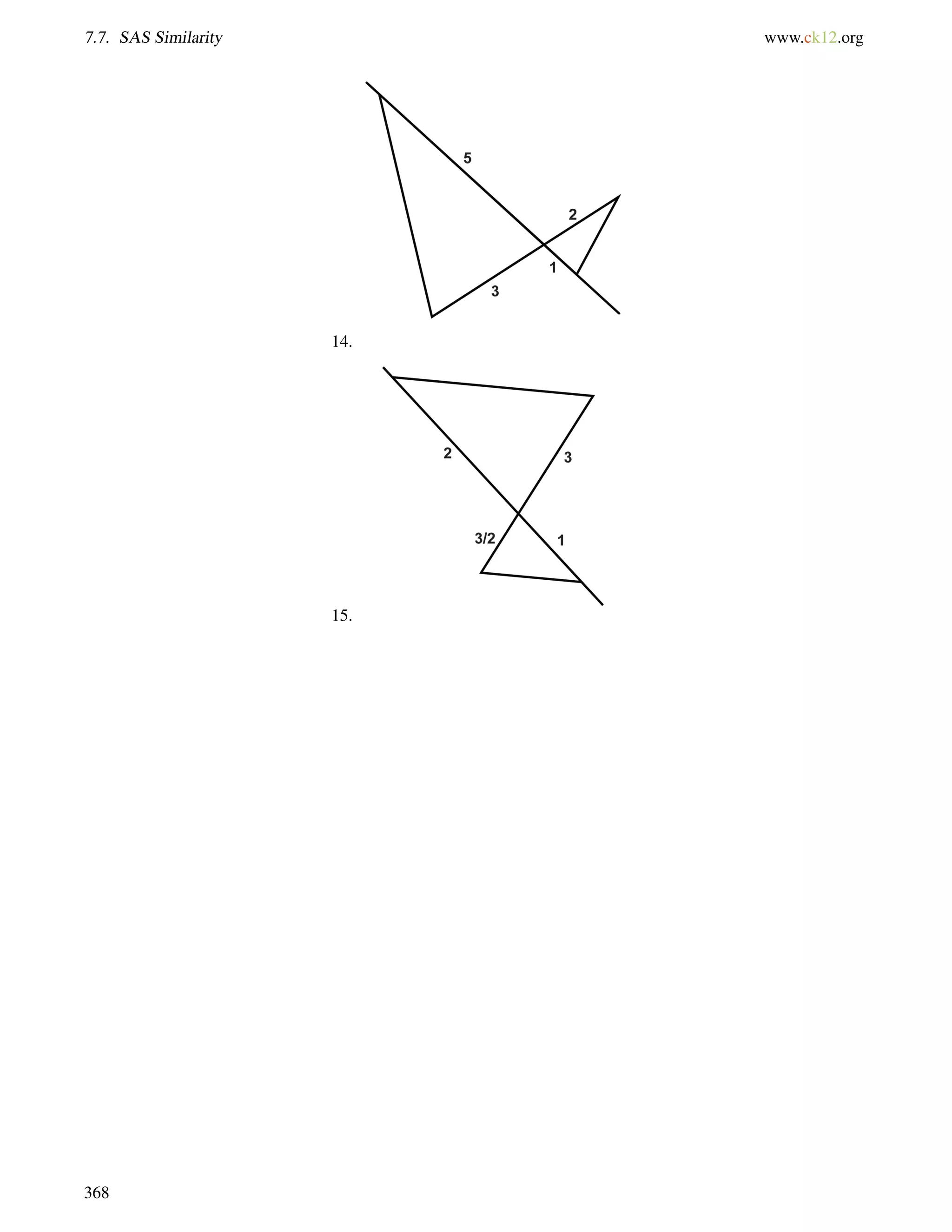
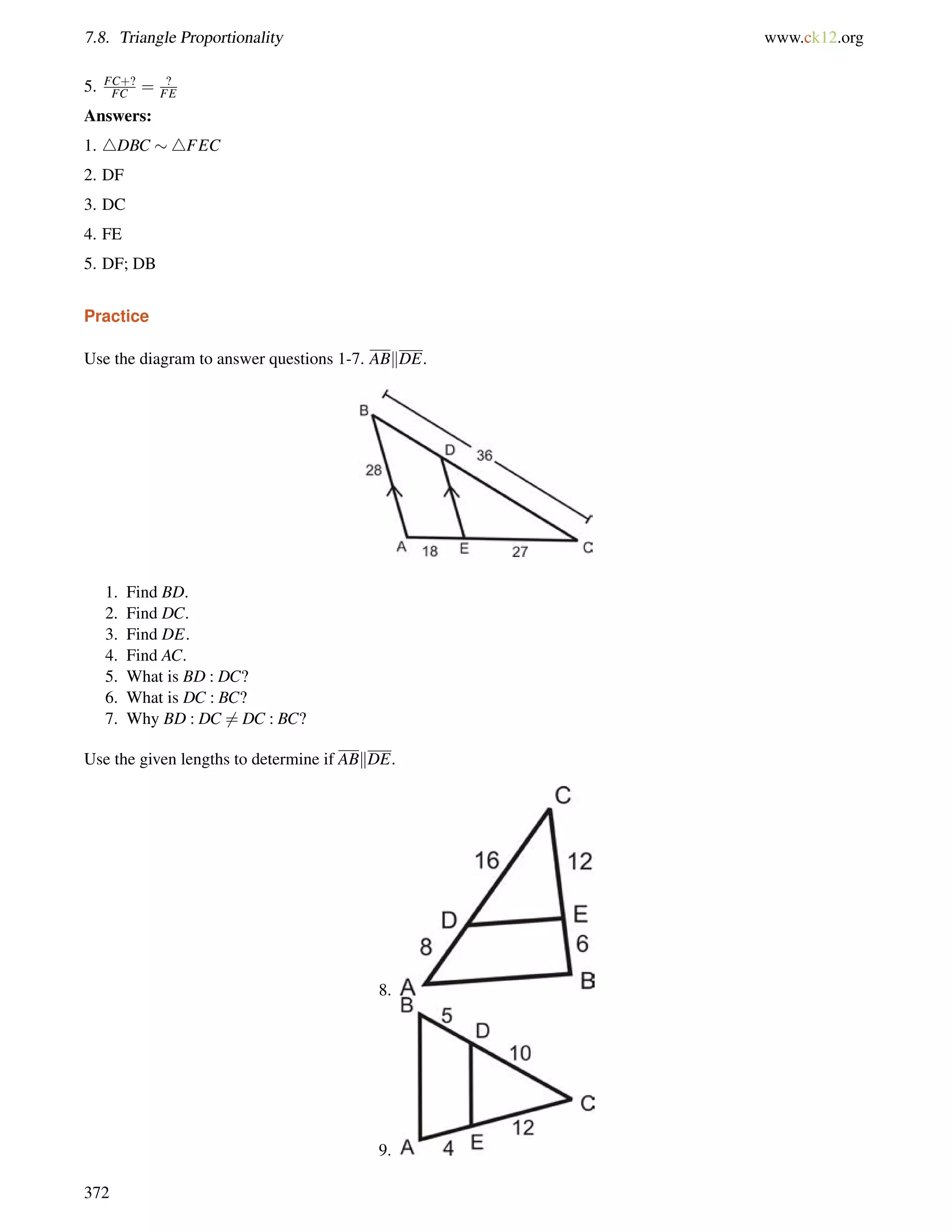
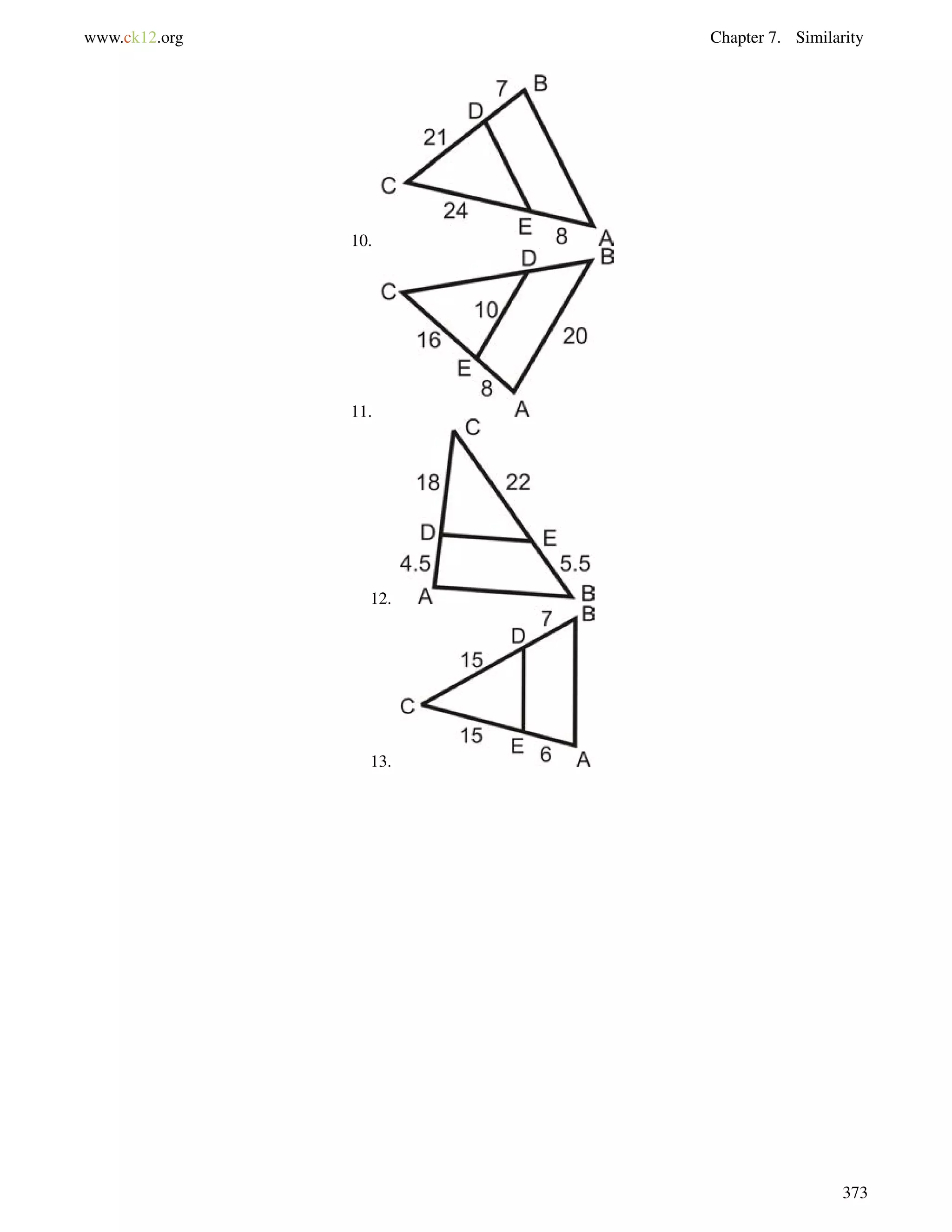
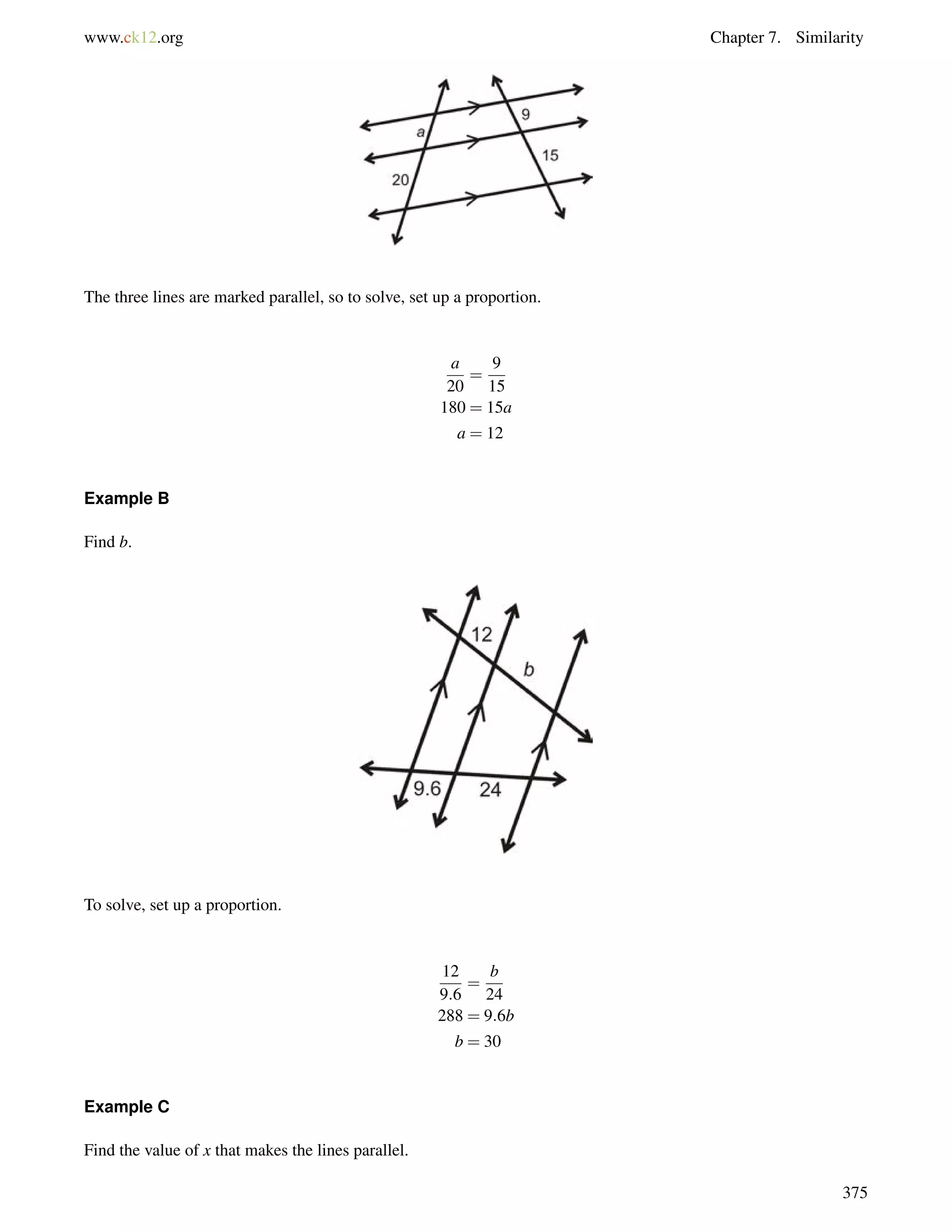
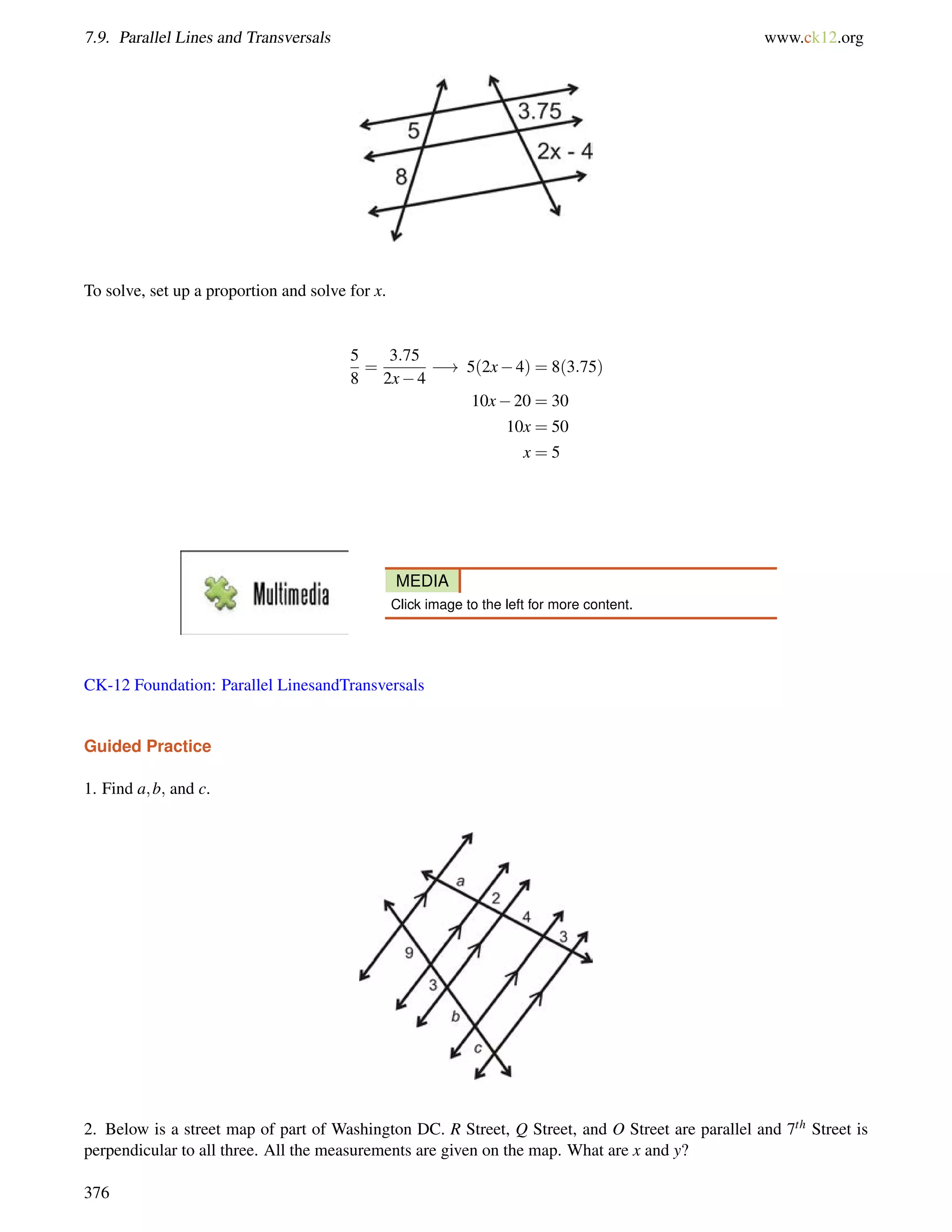
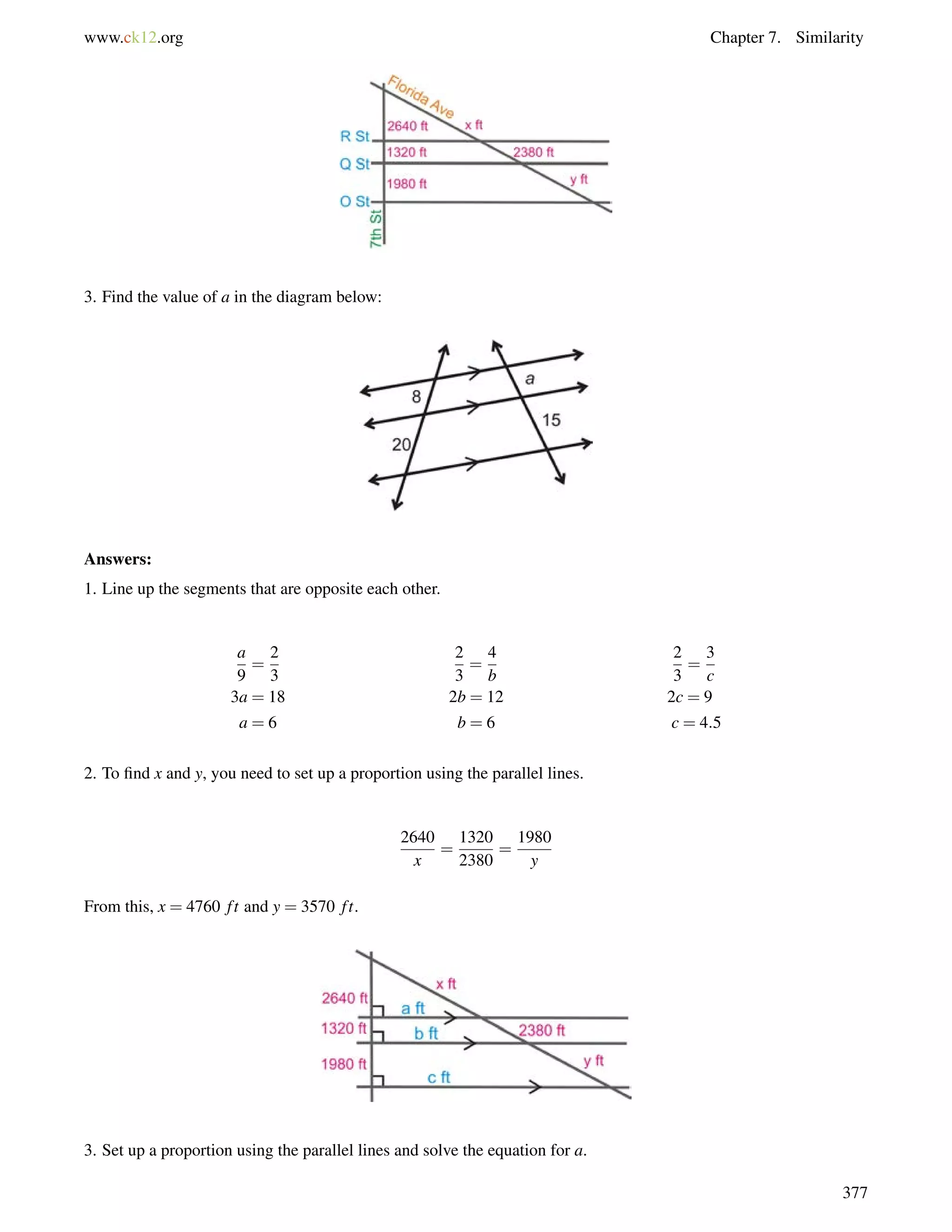
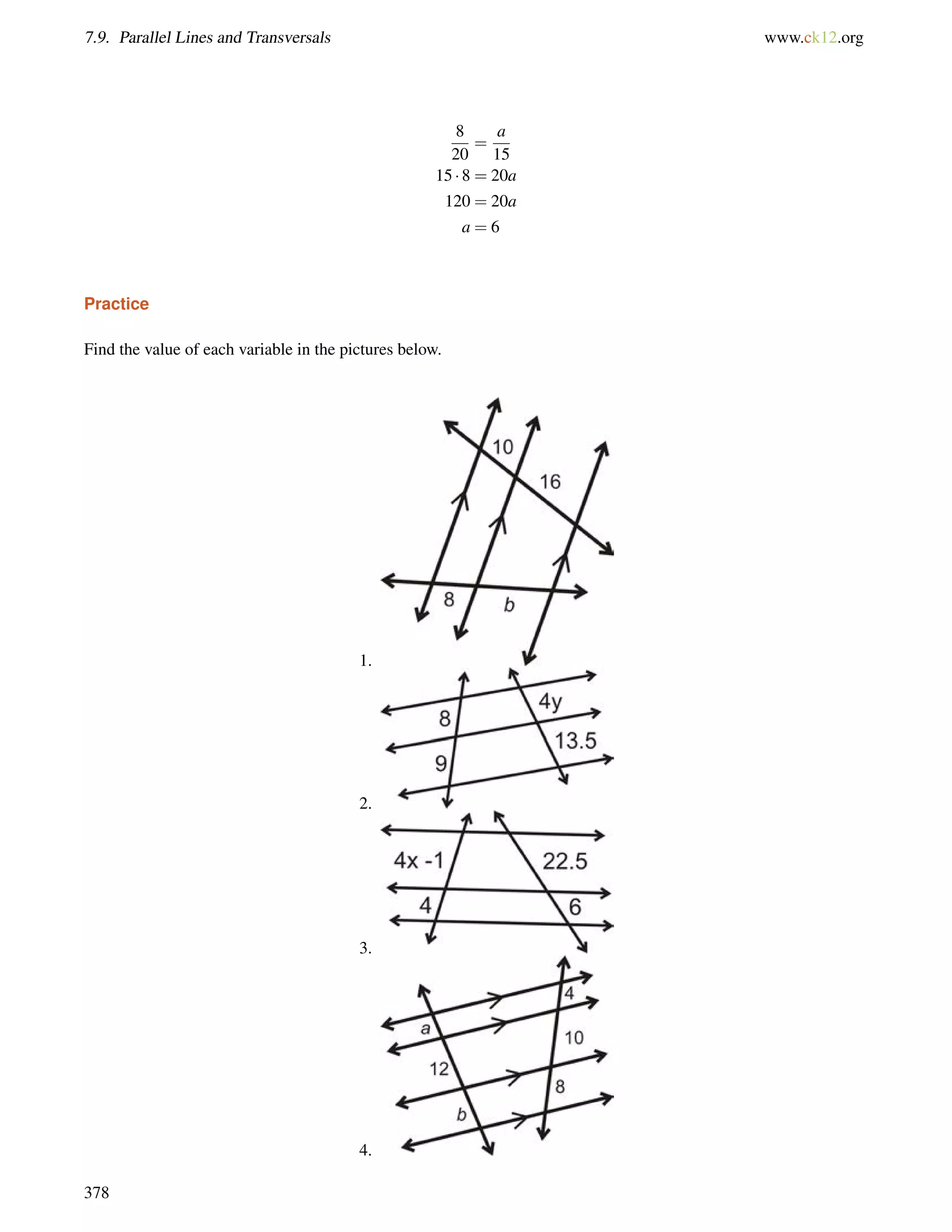
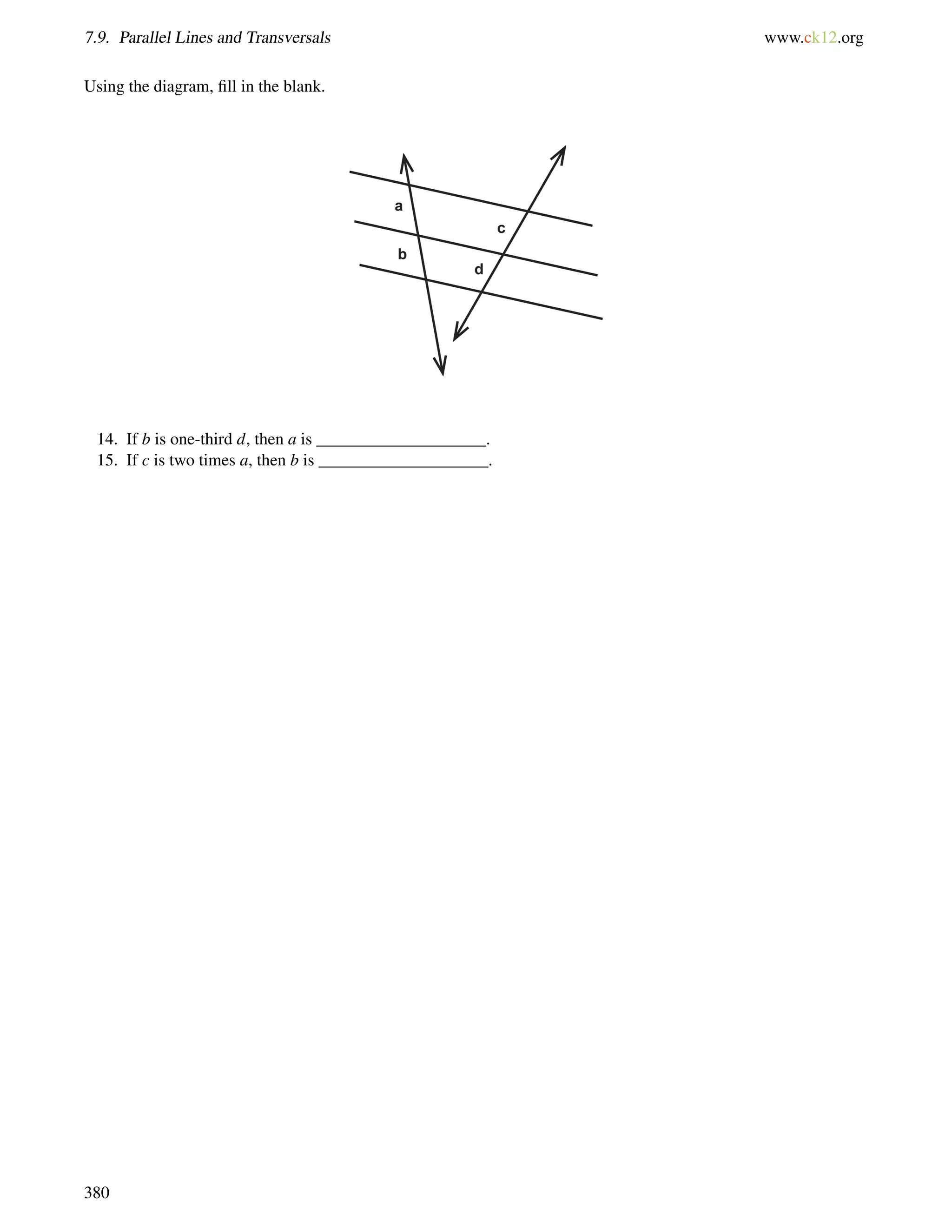
This document is a geometry textbook published by CK-12 Foundation, a nonprofit organization with a mission to reduce textbook costs. It contains 12 chapters covering basic geometry concepts such as lines, angles, triangles, polygons, parallel and perpendicular lines, congruence, similarity, and reasoning and proof. The textbook was authored by Dan Greenberg, Lori Jordan, Andrew Gloag, Victor Cifarelli, Jim Sconyers, and Bill Zahner, and edited by Annamaria Farbizio.



















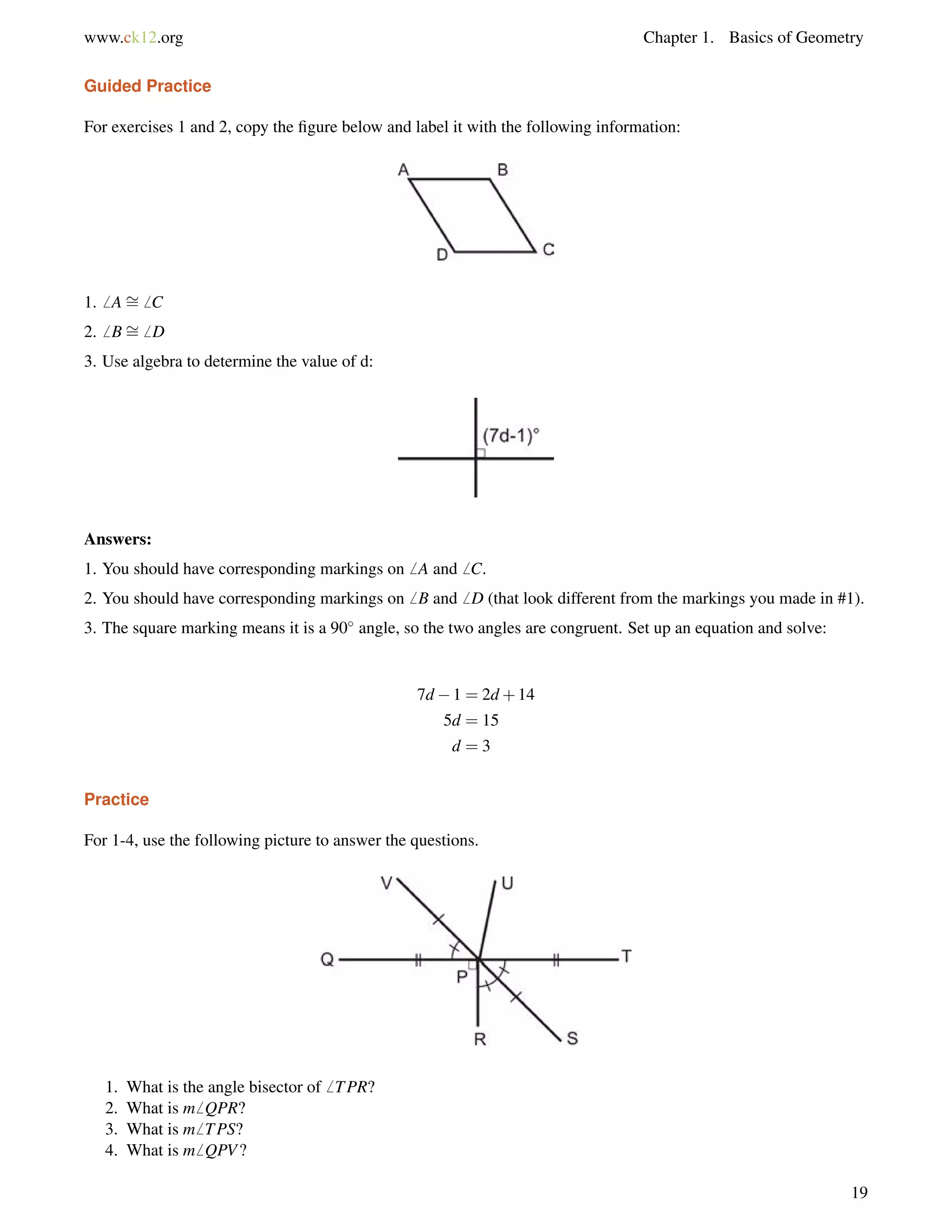























































































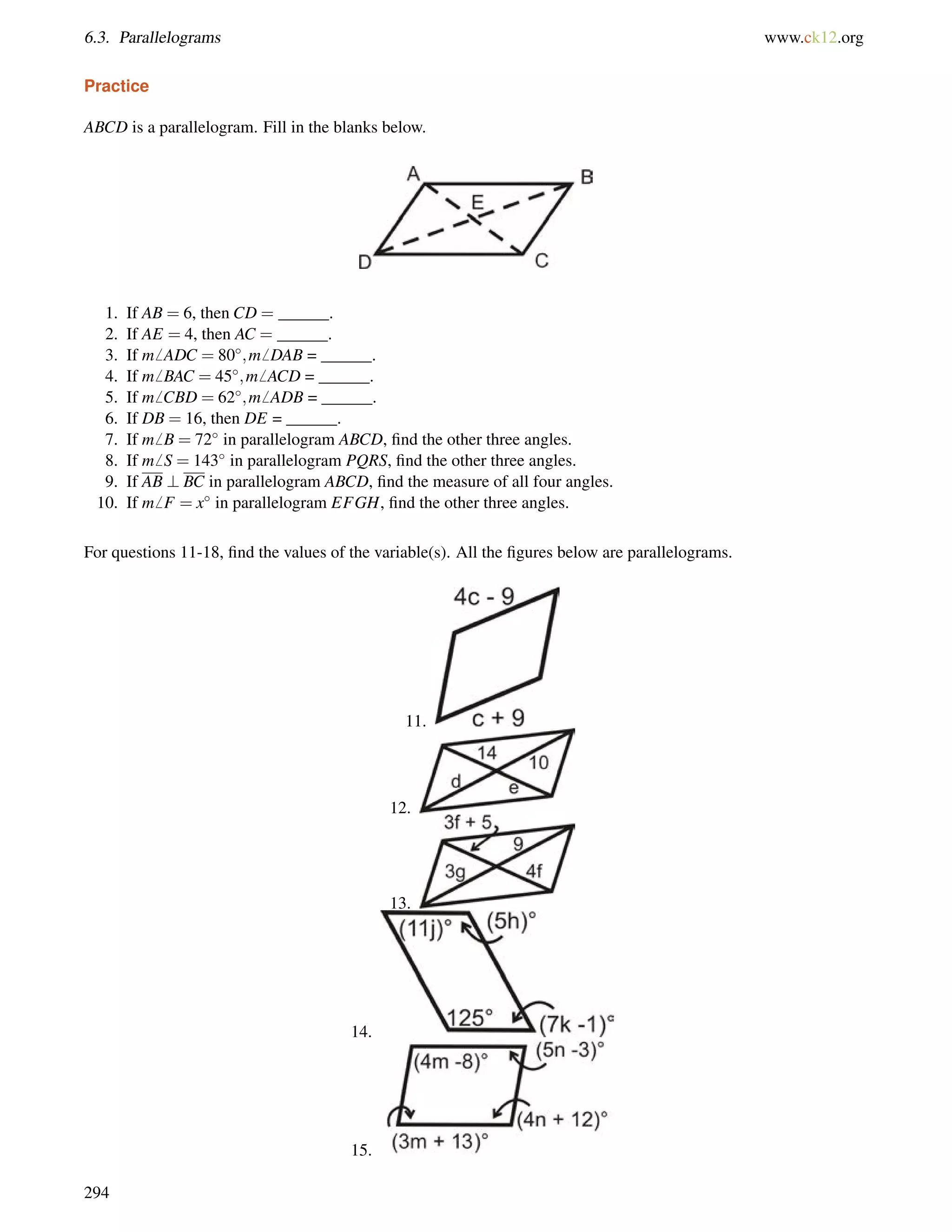
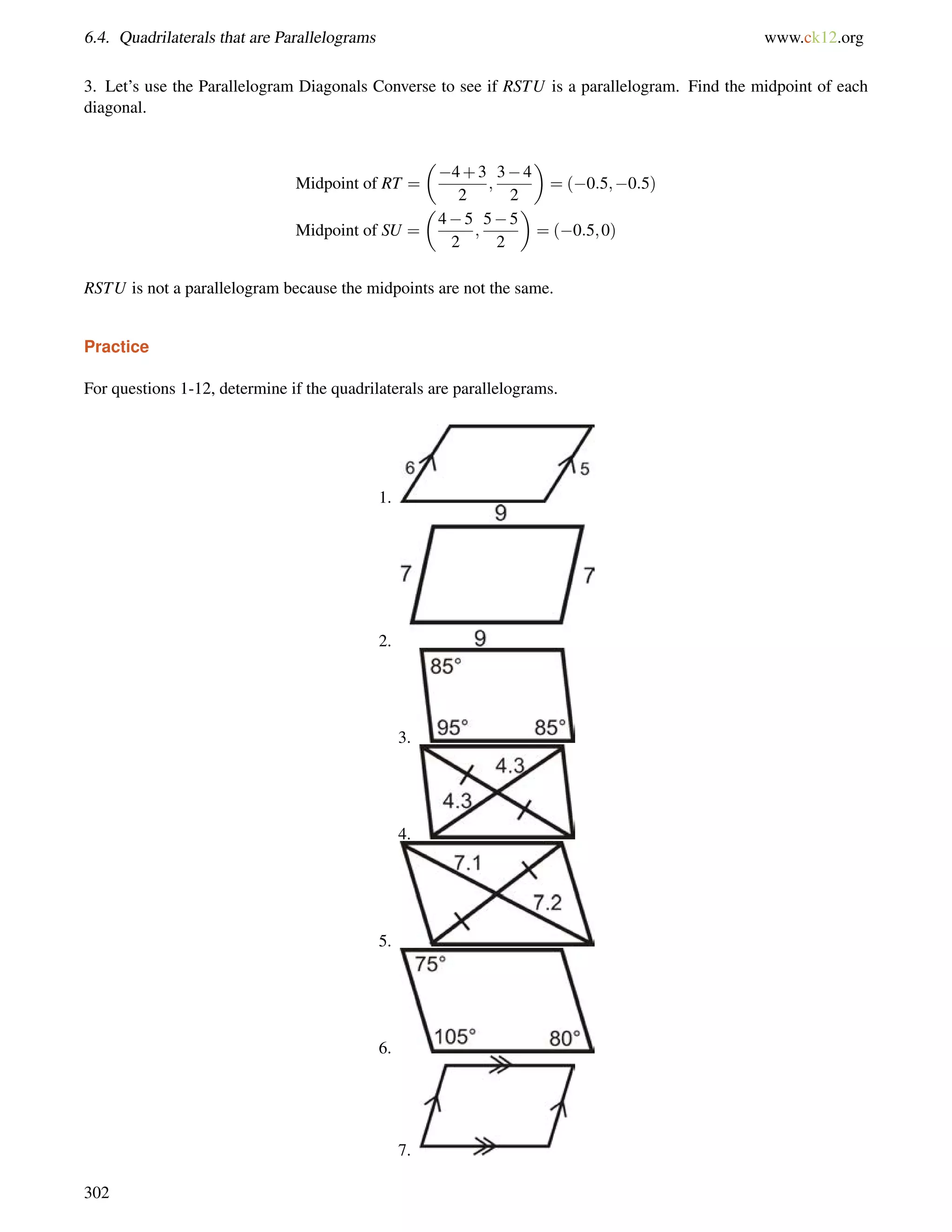
![3.5. Alternate Exterior Angles www.ck12.org
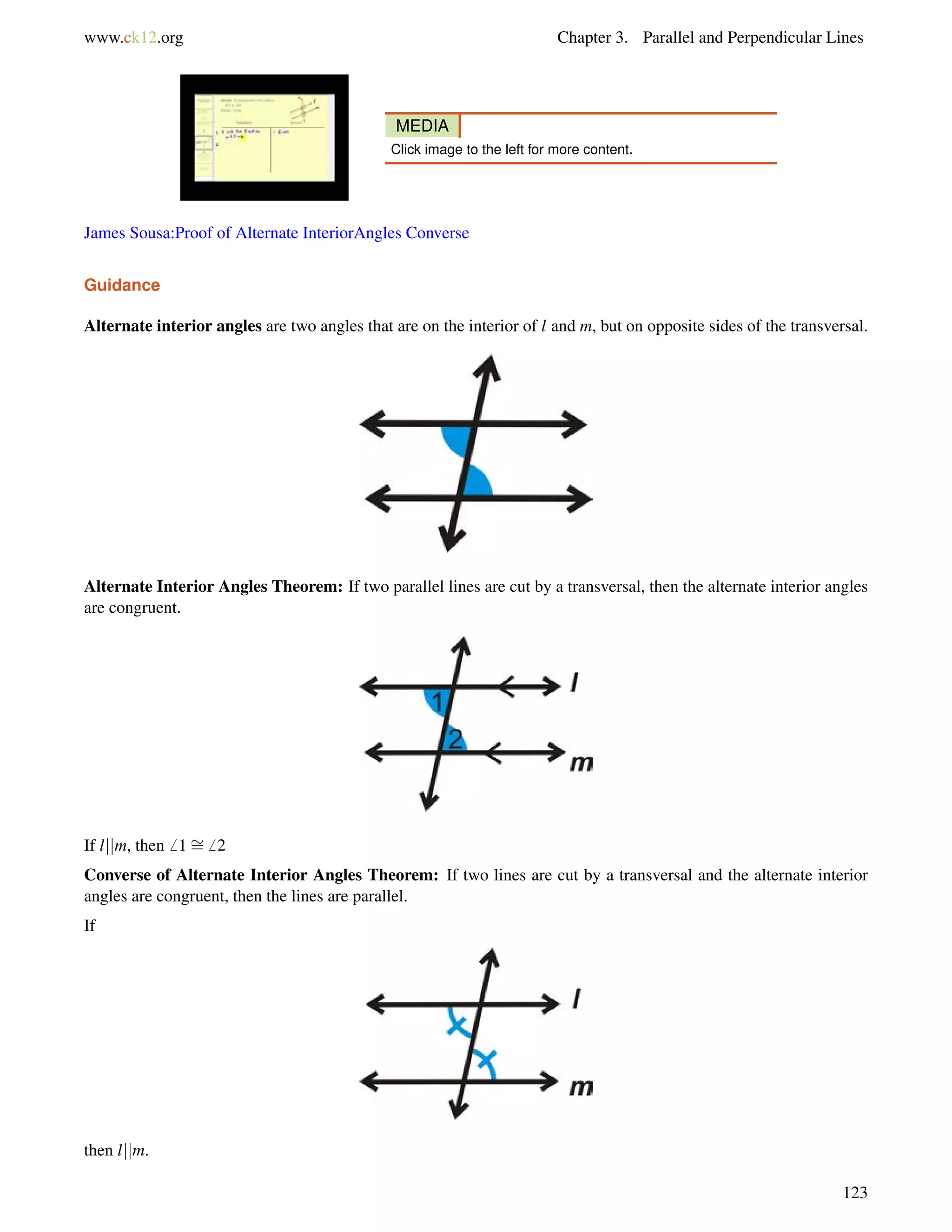
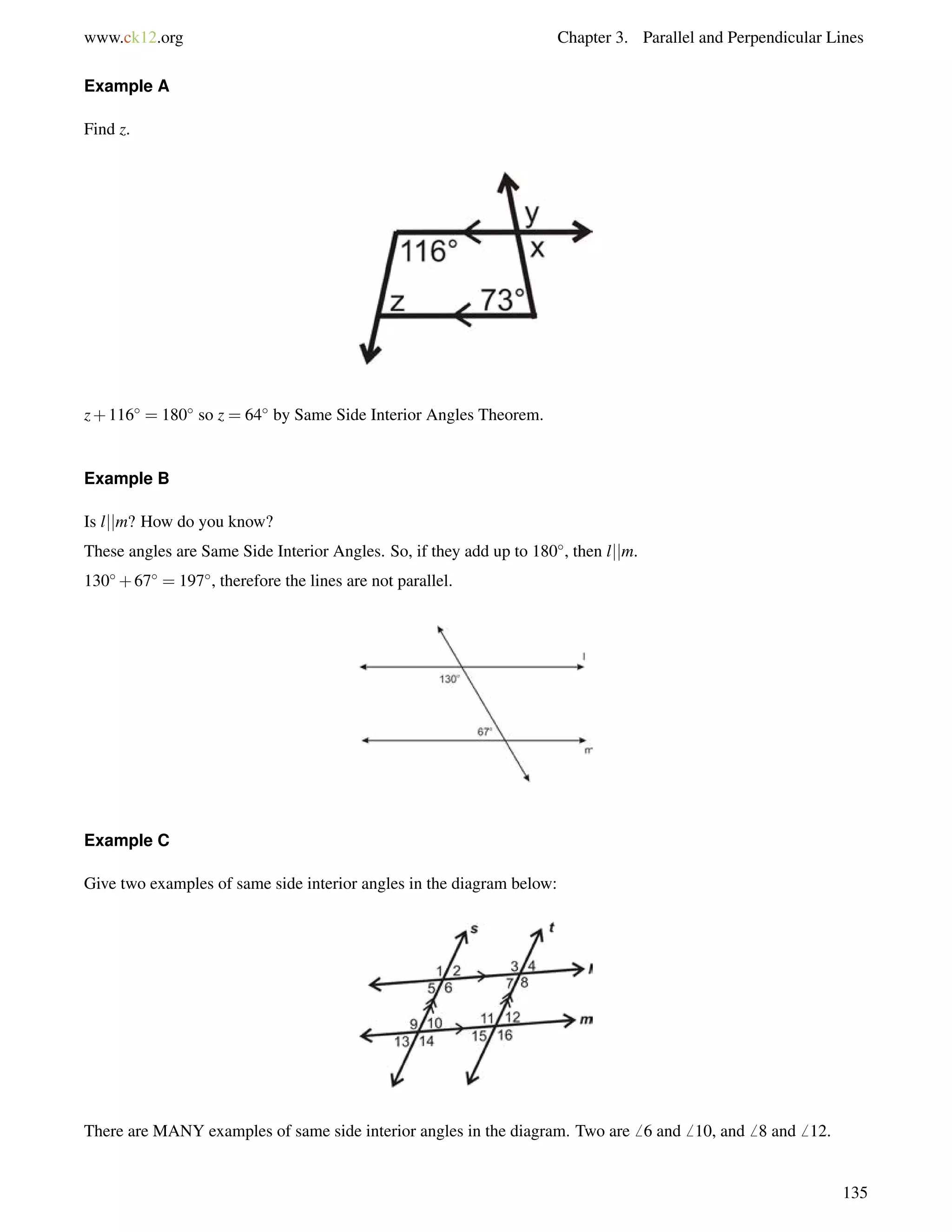
The angles are alternate exterior angles. Because the lines are parallel, the angles are equal.
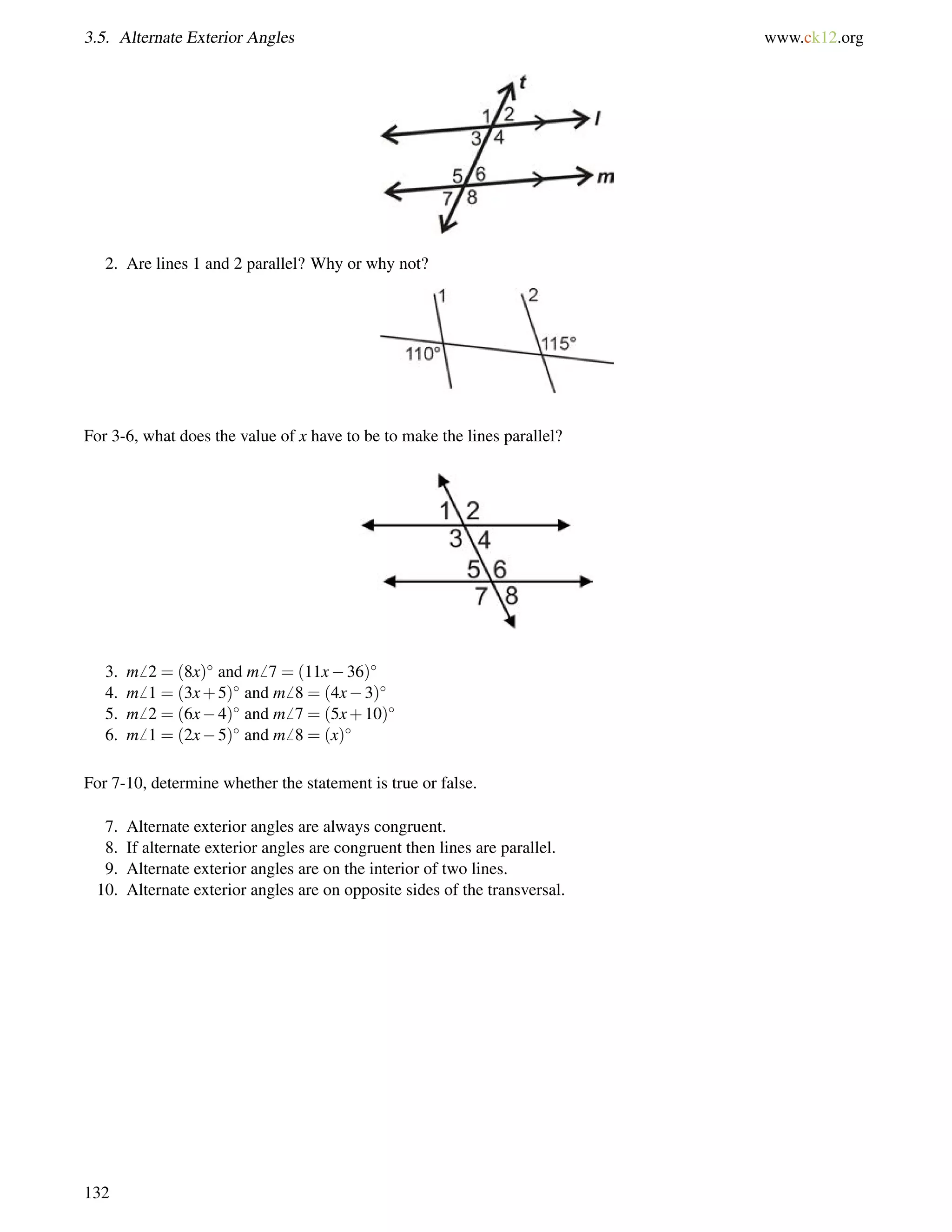
(3y+53) = (7y55)
108 = 4y
27 = y
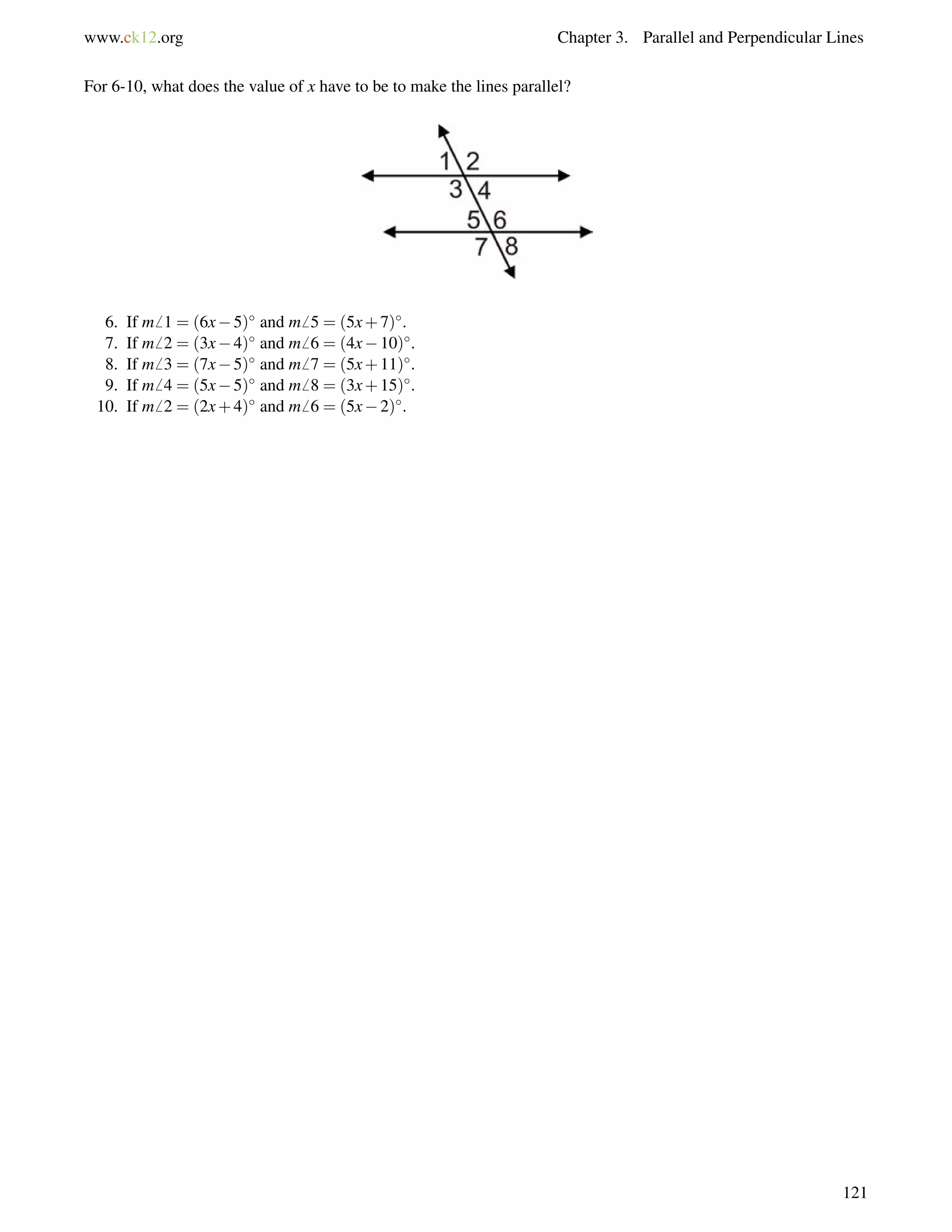
If y = 27, then each angle is [3(27)+53] = 134.
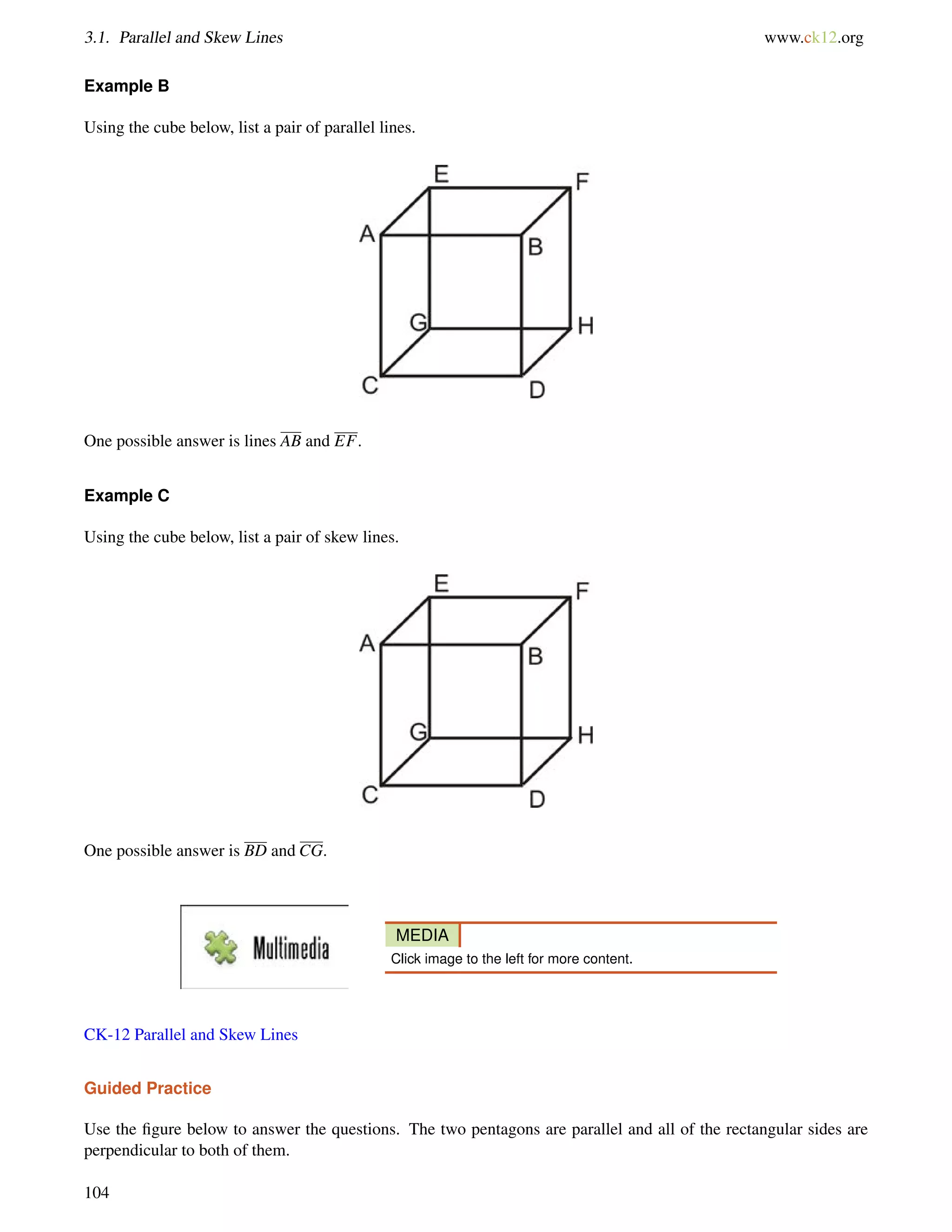
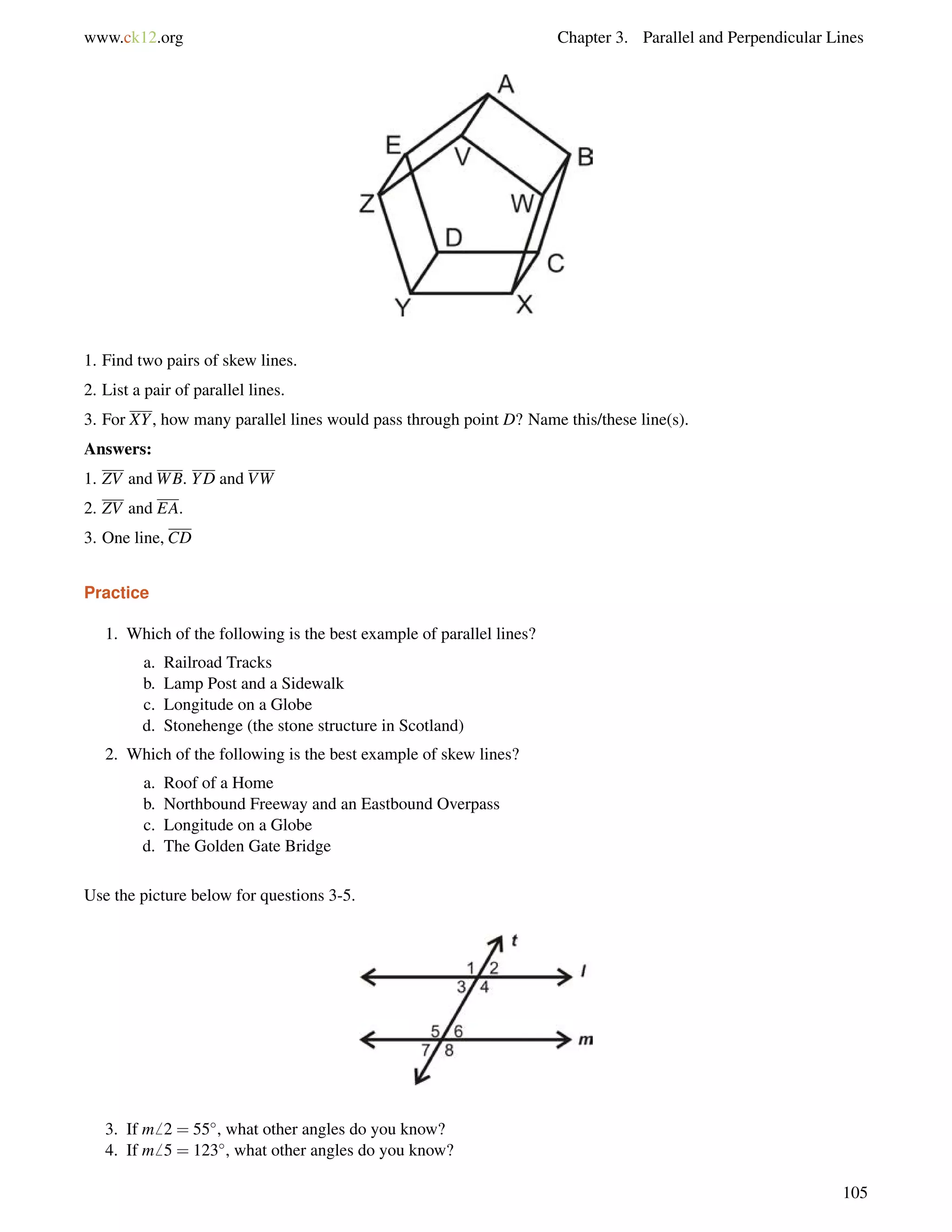
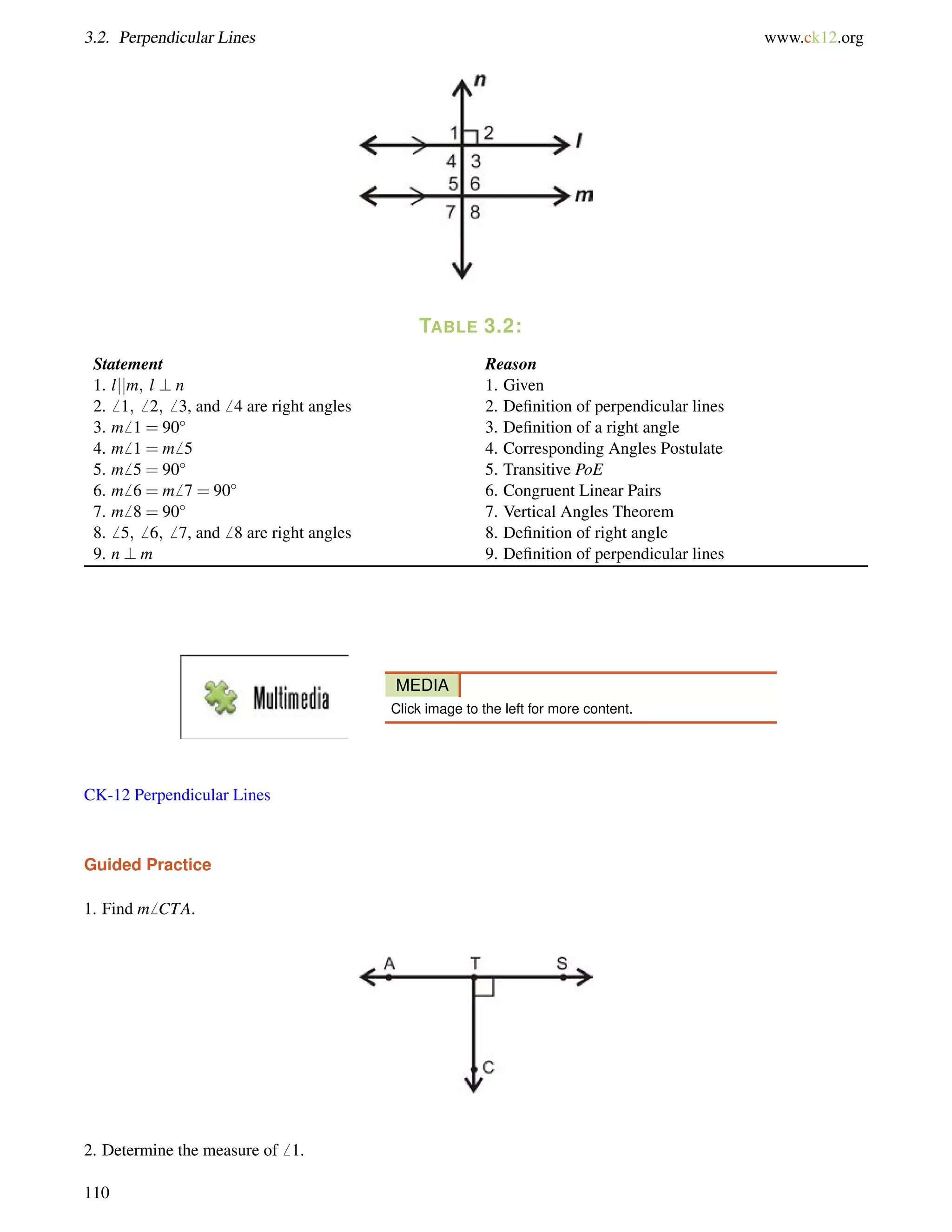
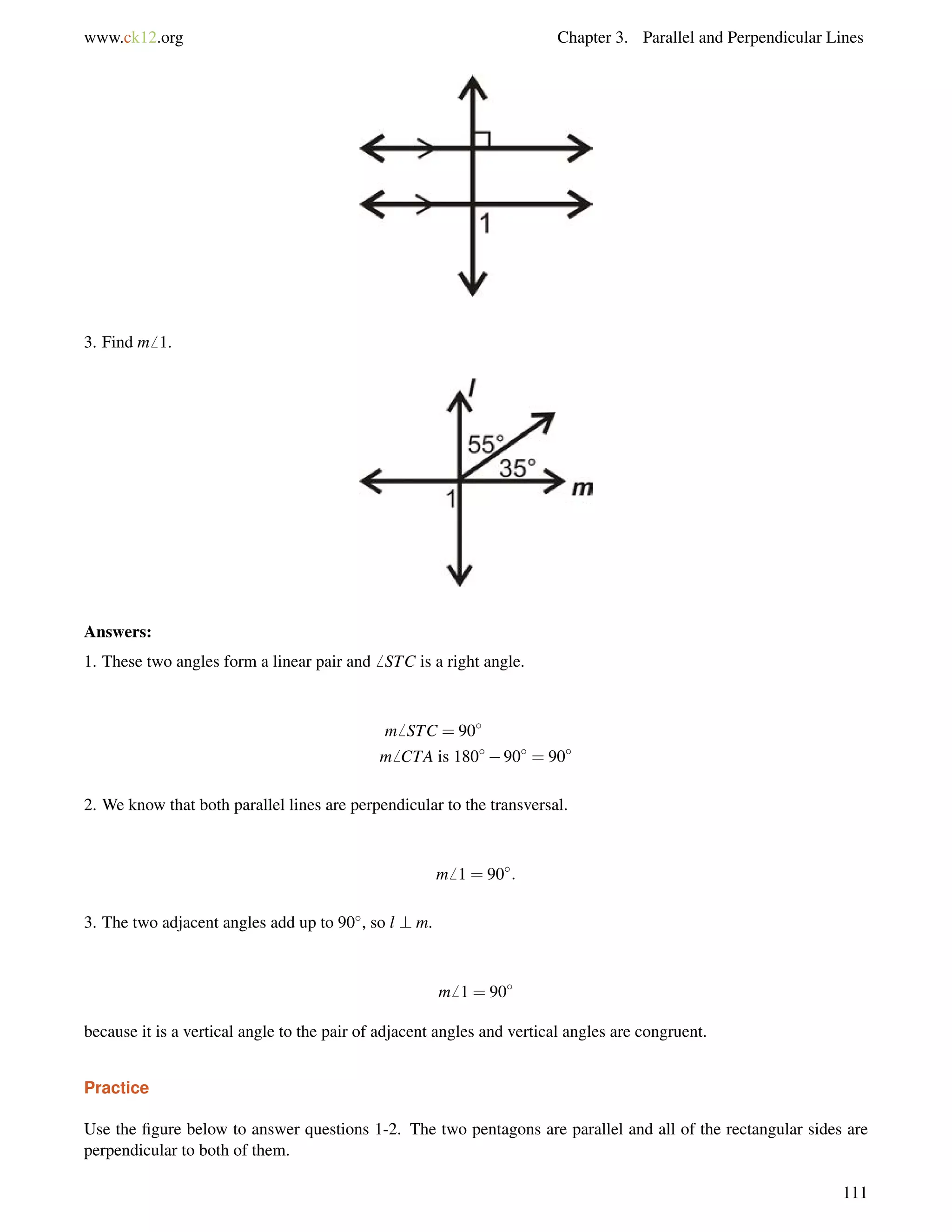
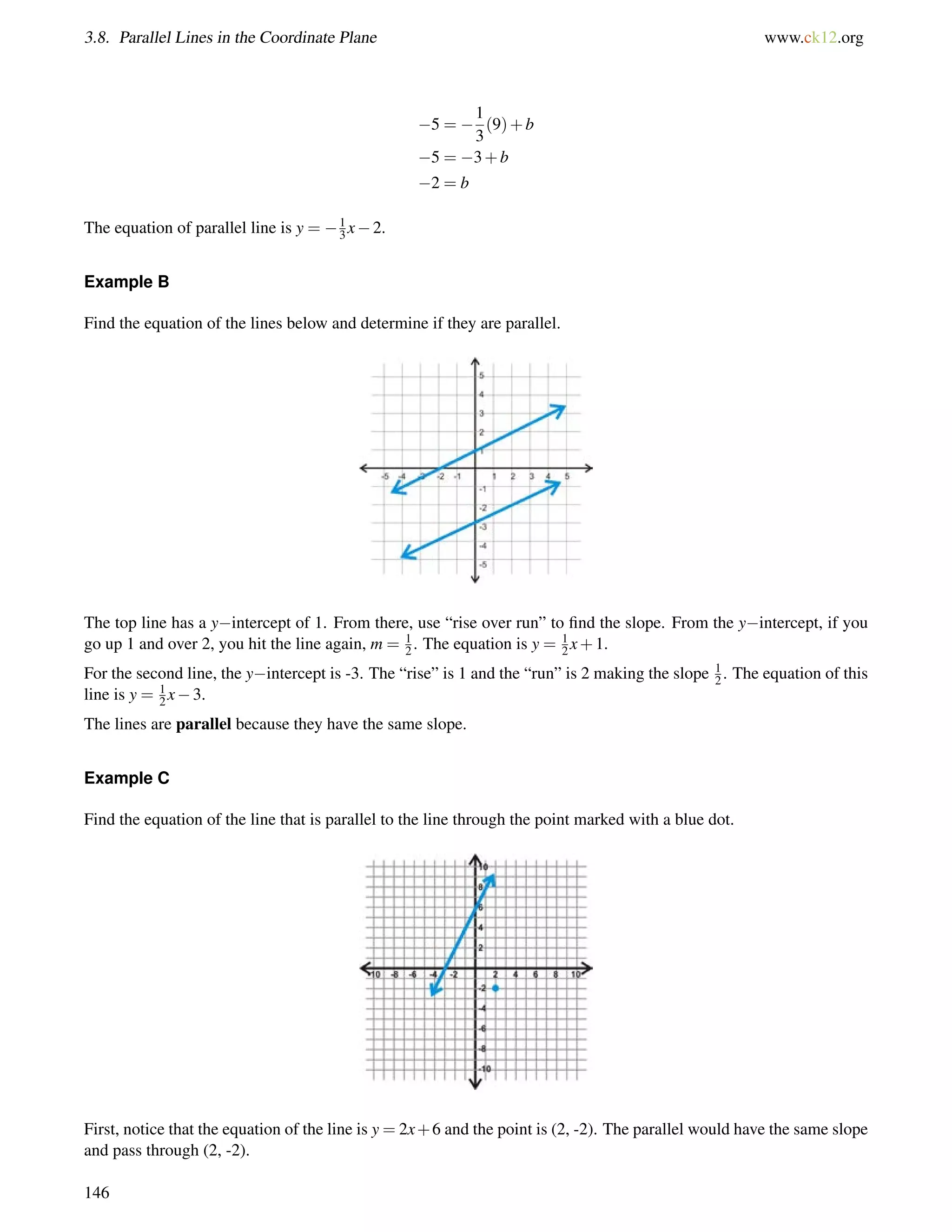
Example B
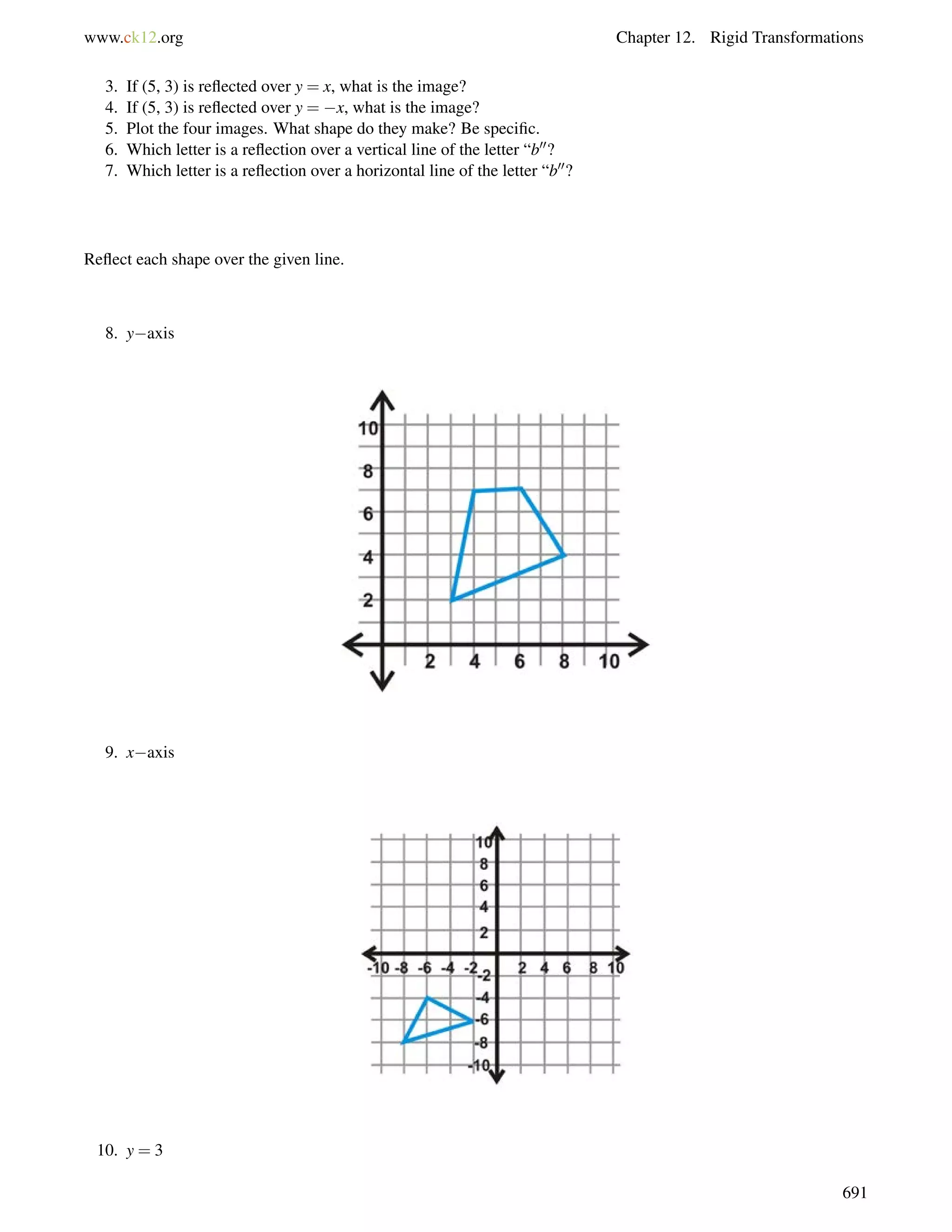
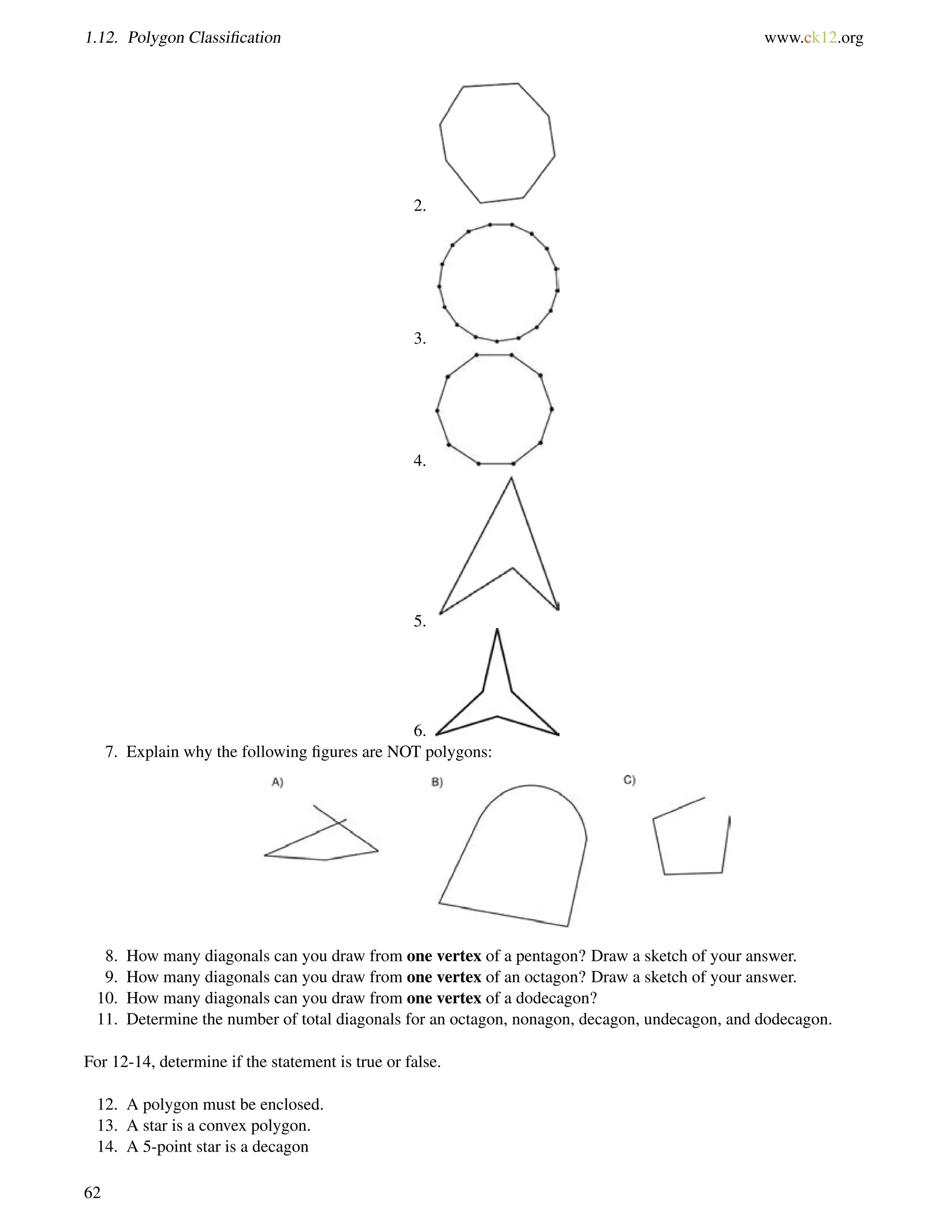
The map below shows three roads in Julio’s town.
Julio used a surveying tool to measure two angles at the intersections in this picture he drew (NOT to scale). Julio
wants to know if Franklin Way is parallel to Chavez Avenue.
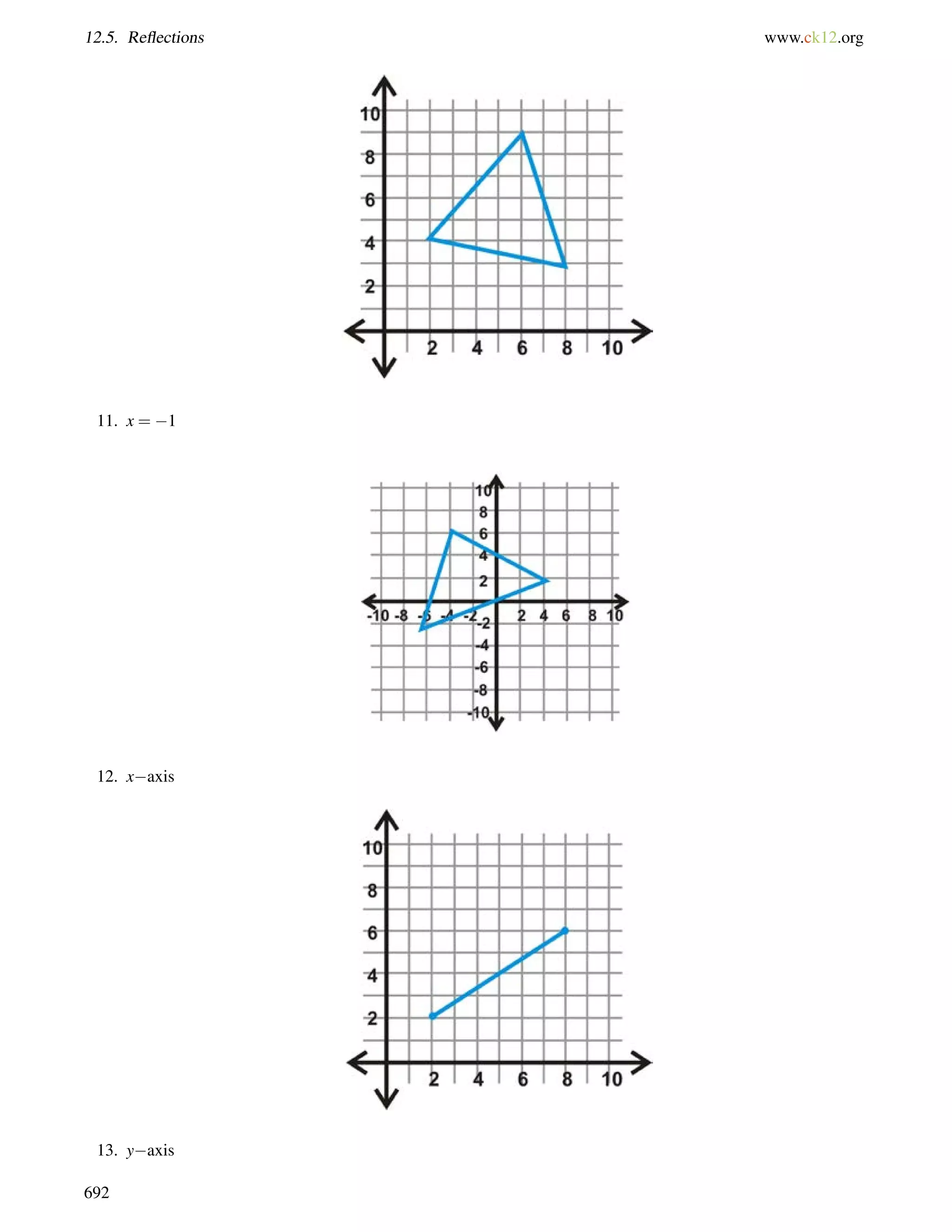
The 130 angle and6 a are alternate exterior angles. If m6 a = 130, then the lines are parallel.
6 a+40 = 180 by the Linear Pair Postulate
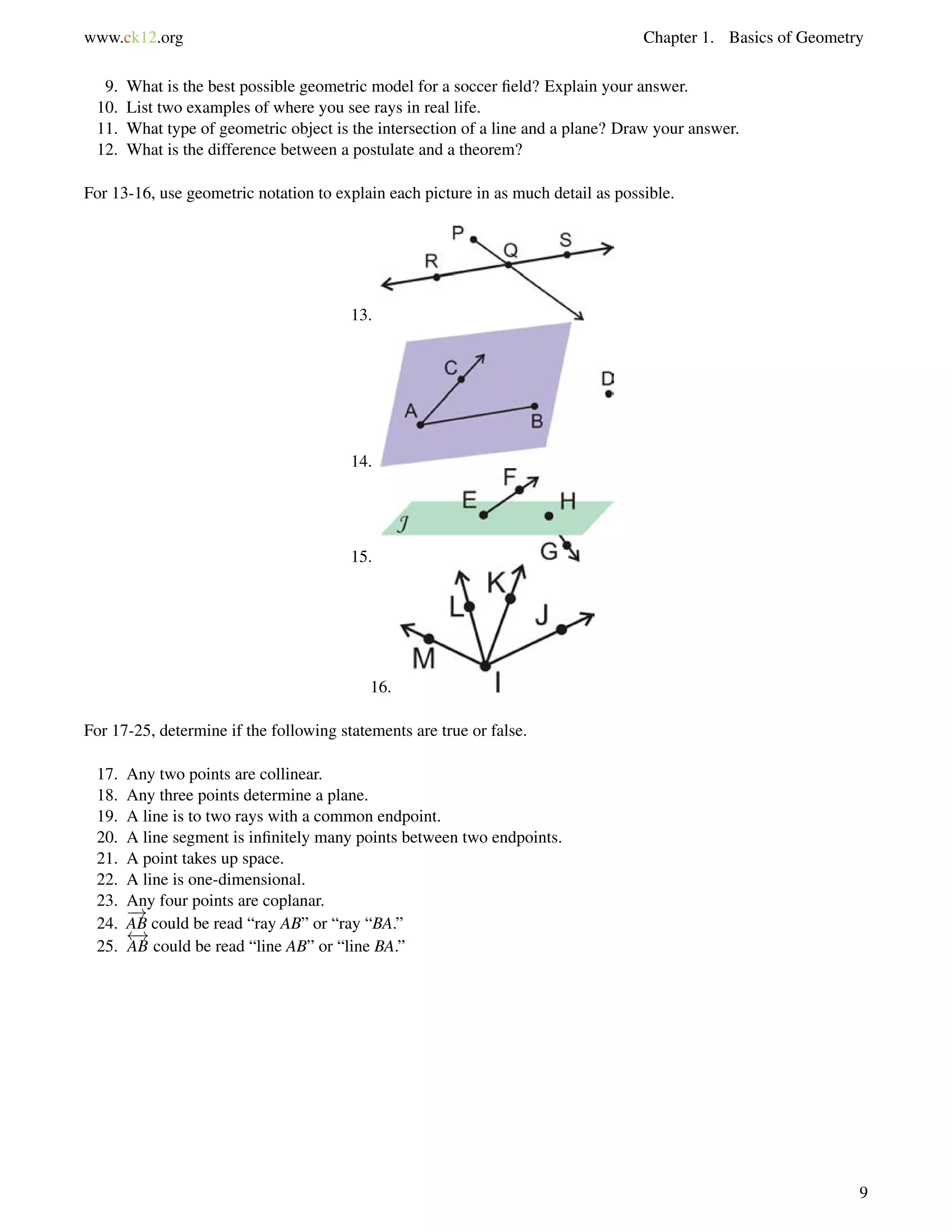
6 a = 140
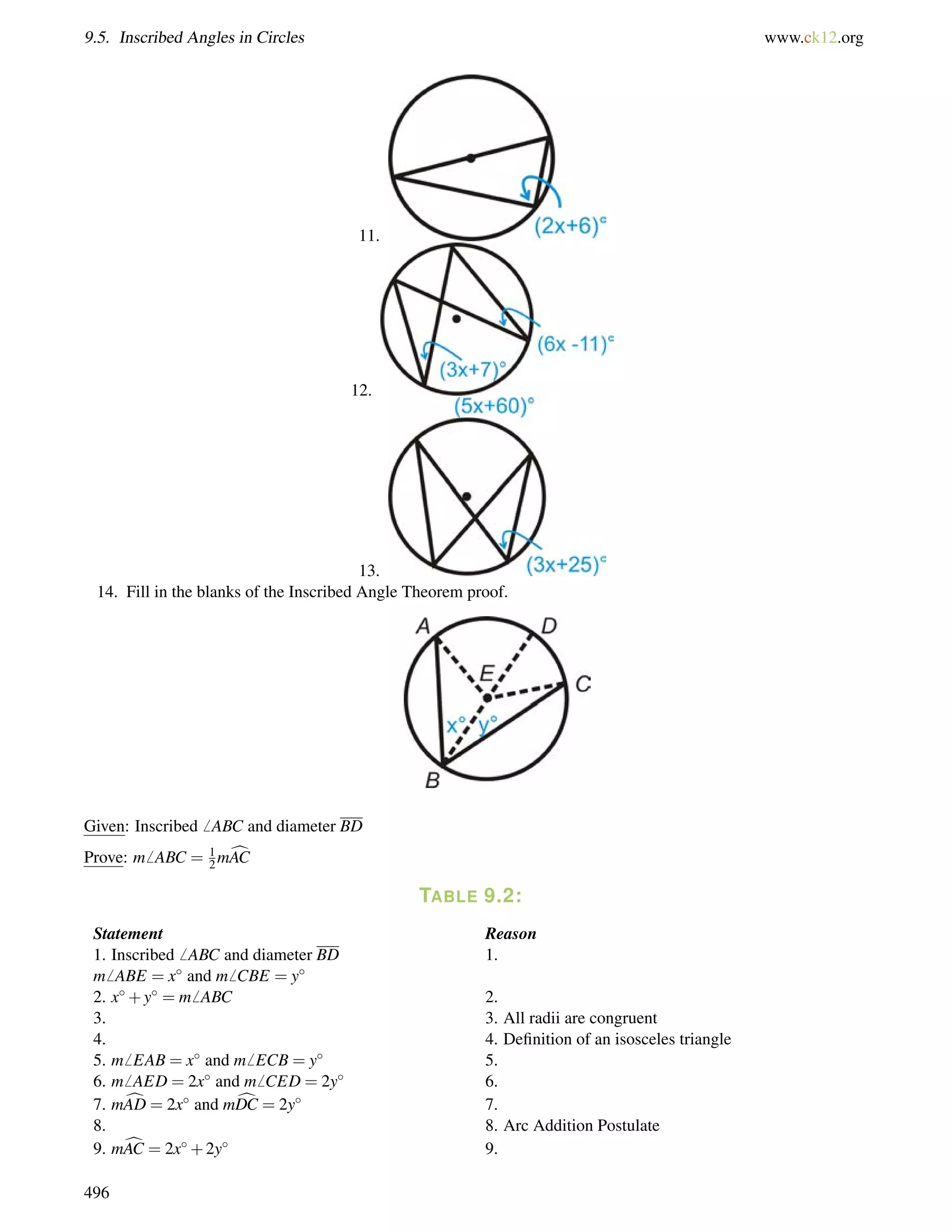
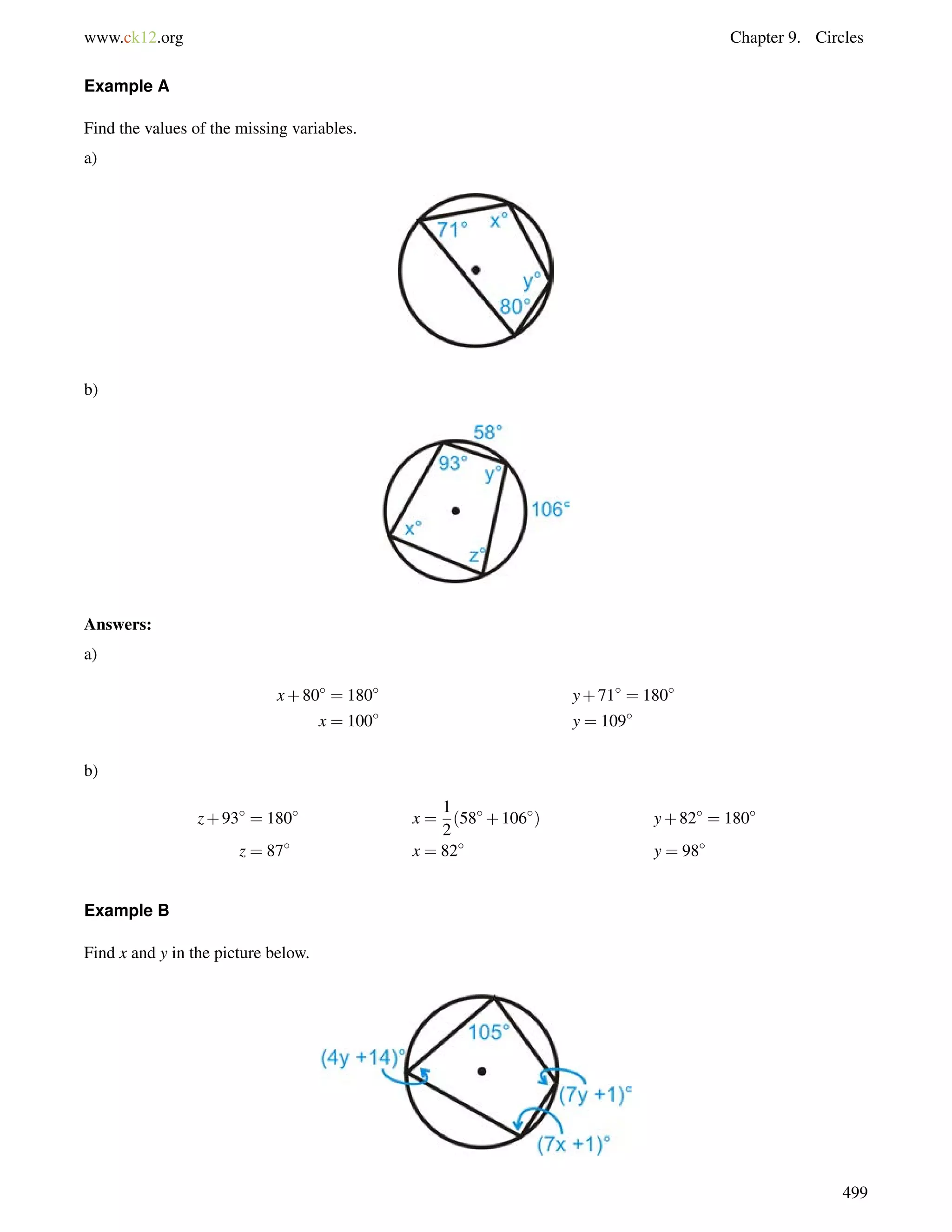
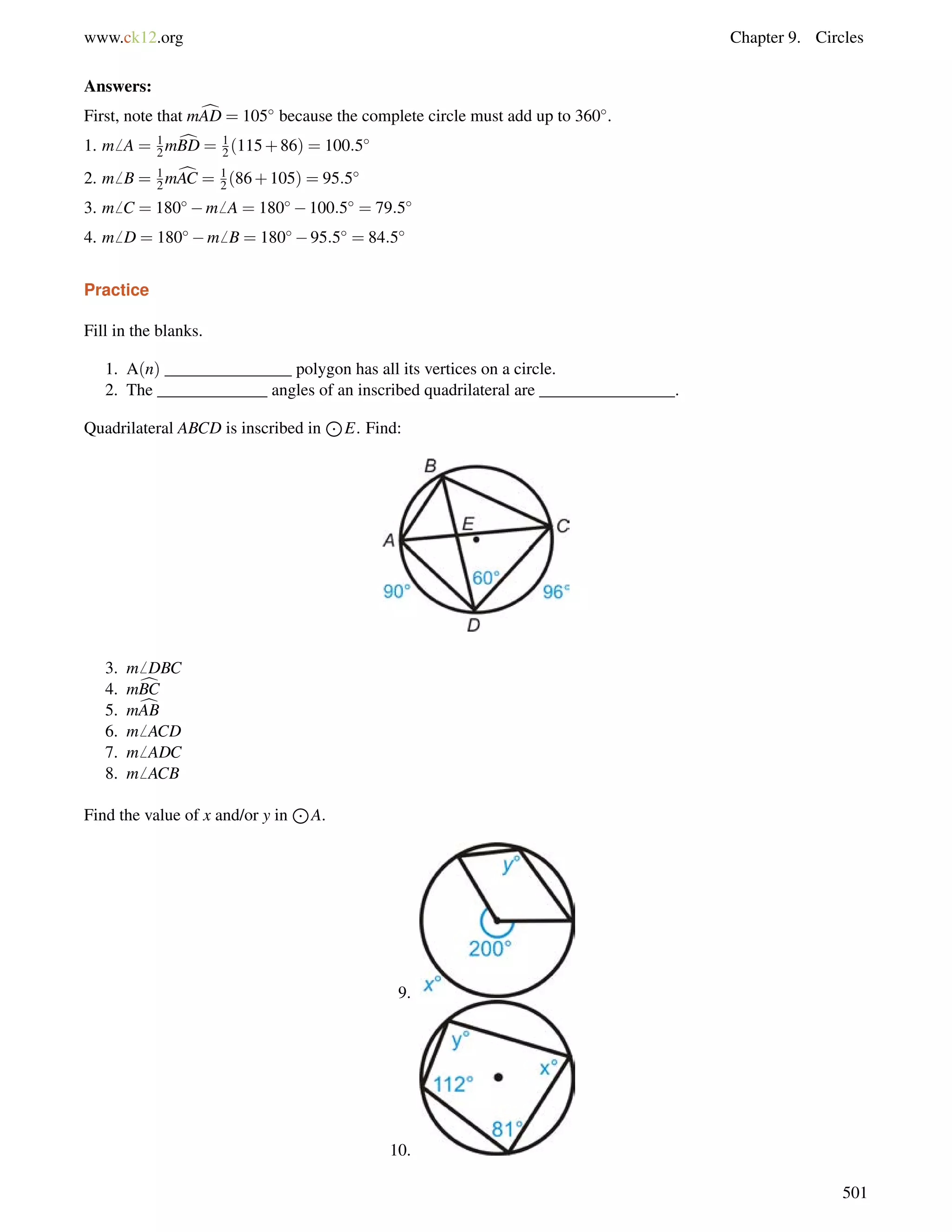
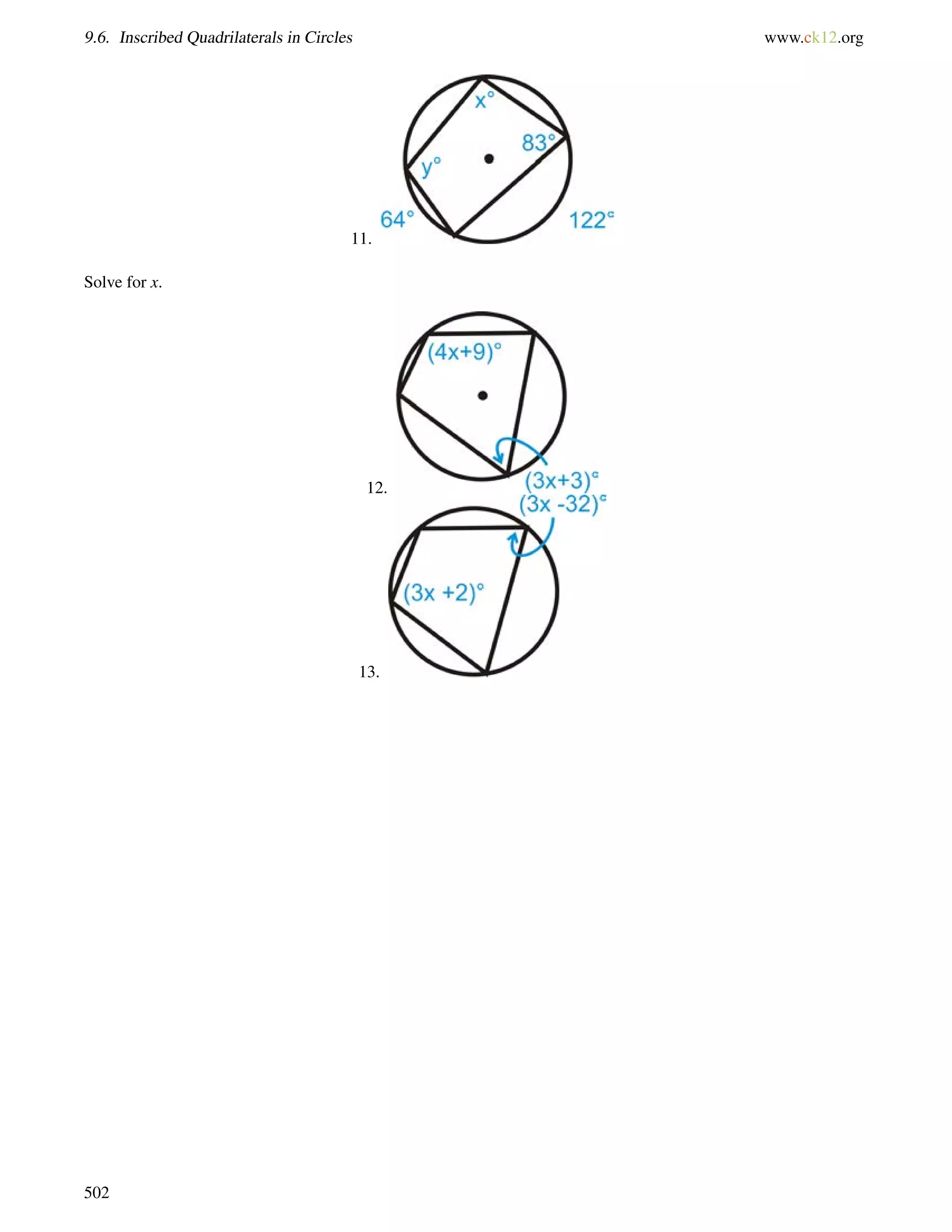
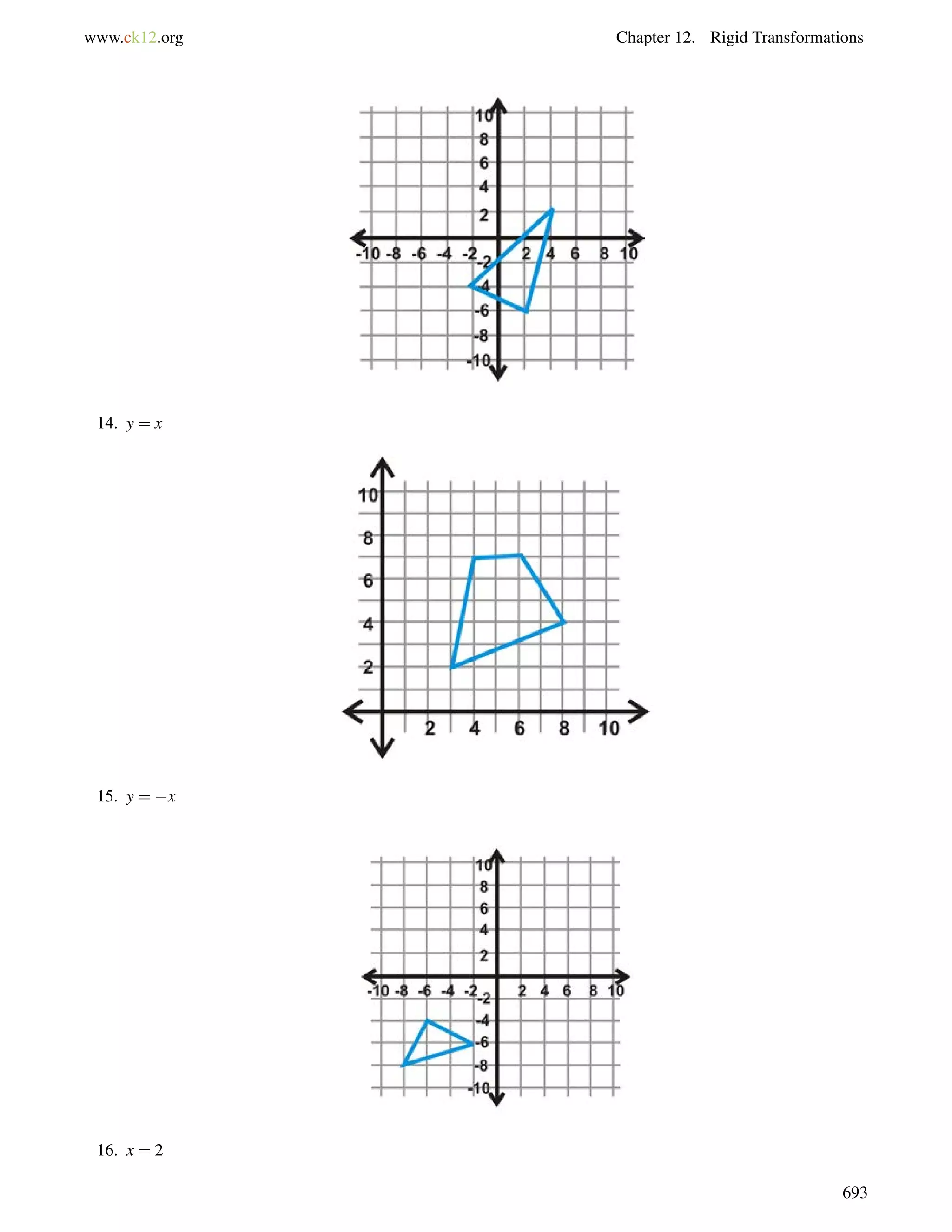
1406= 130, so Franklin Way and Chavez Avenue are not parallel streets.
Example C
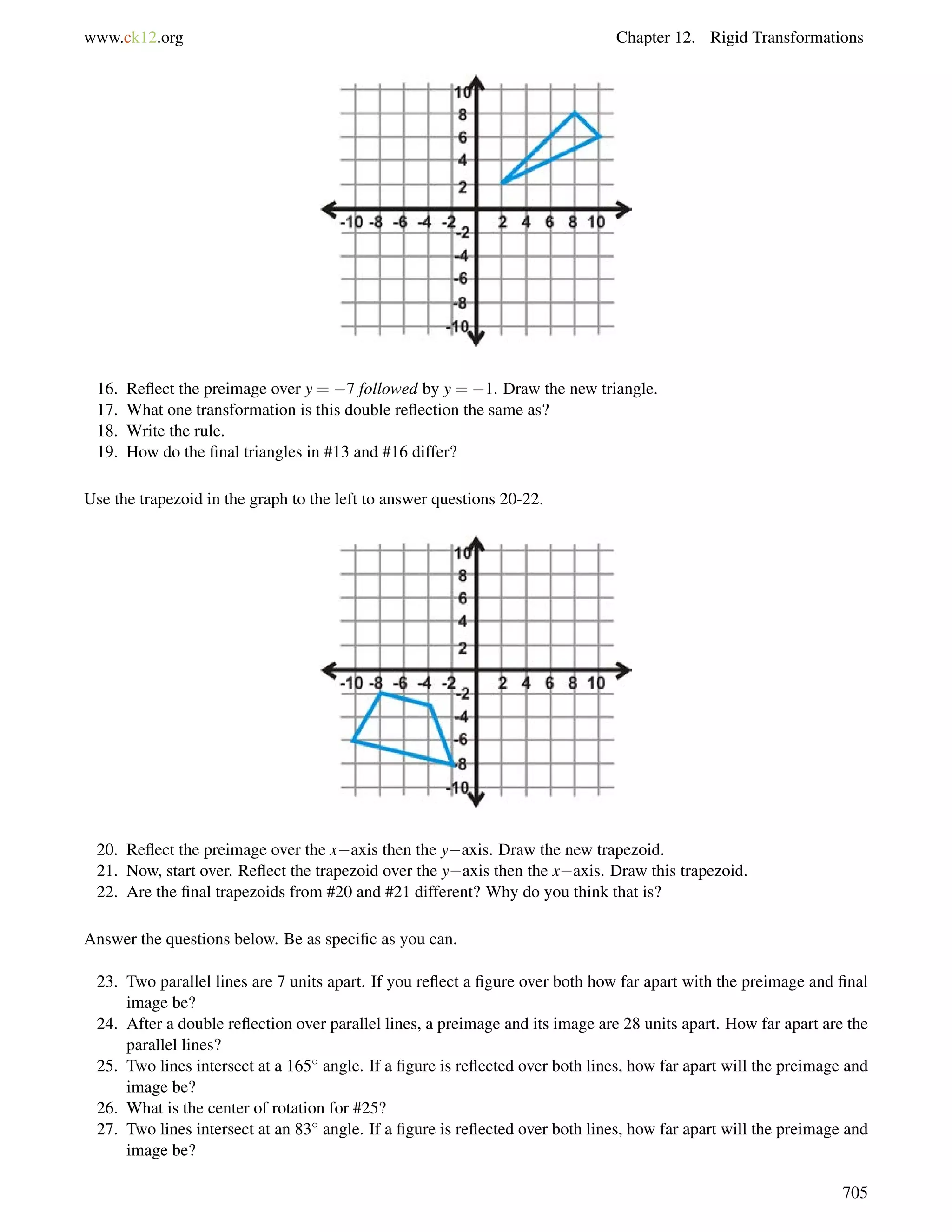
Which lines are parallel if6 AFG=
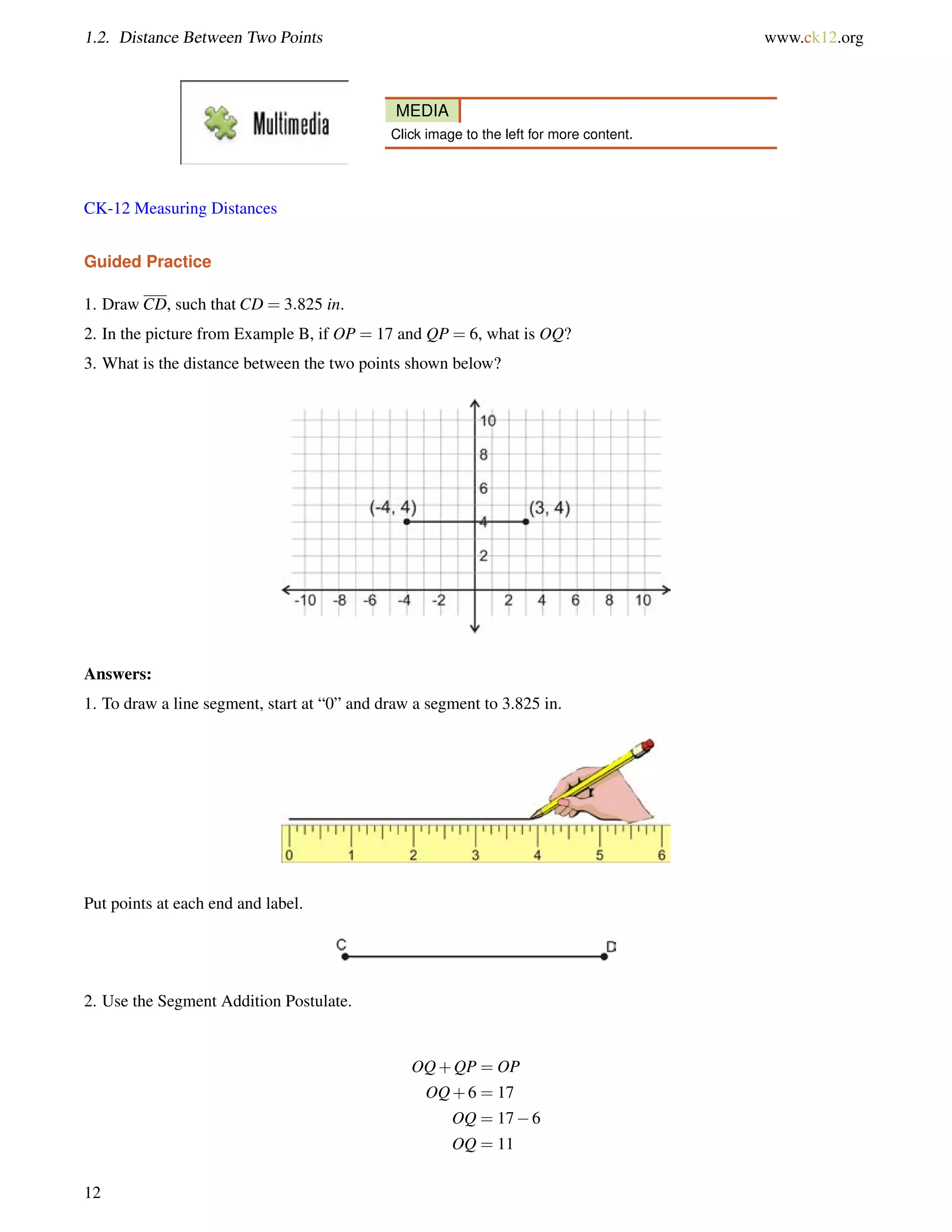
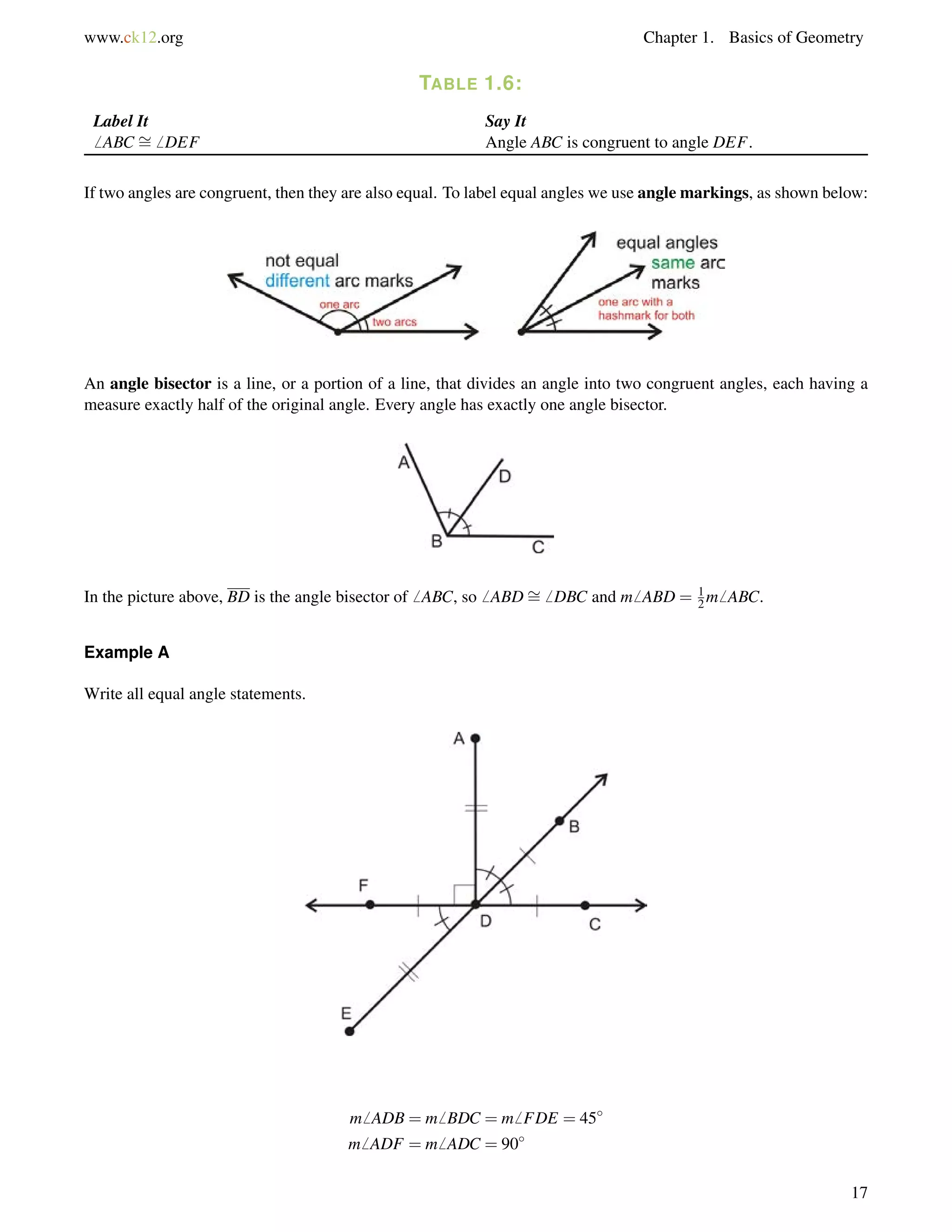
6 IJM?
130](https://image.slidesharecdn.com/ck-12-basic-geometry-conceptsbv10tfrs1reduced-141002074324-phpapp01/75/Ck-12-basic-geometry-concepts-136-2048.jpg)





















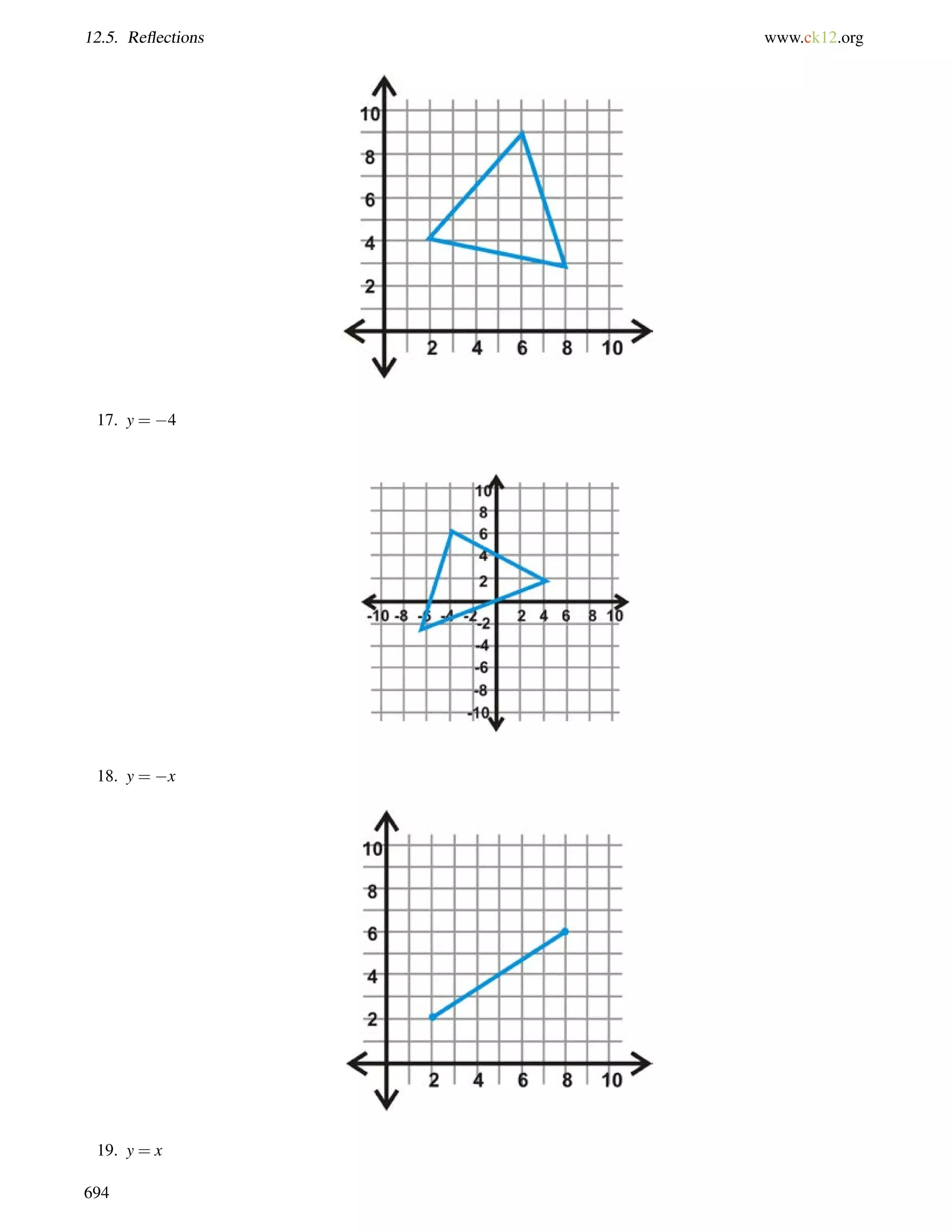
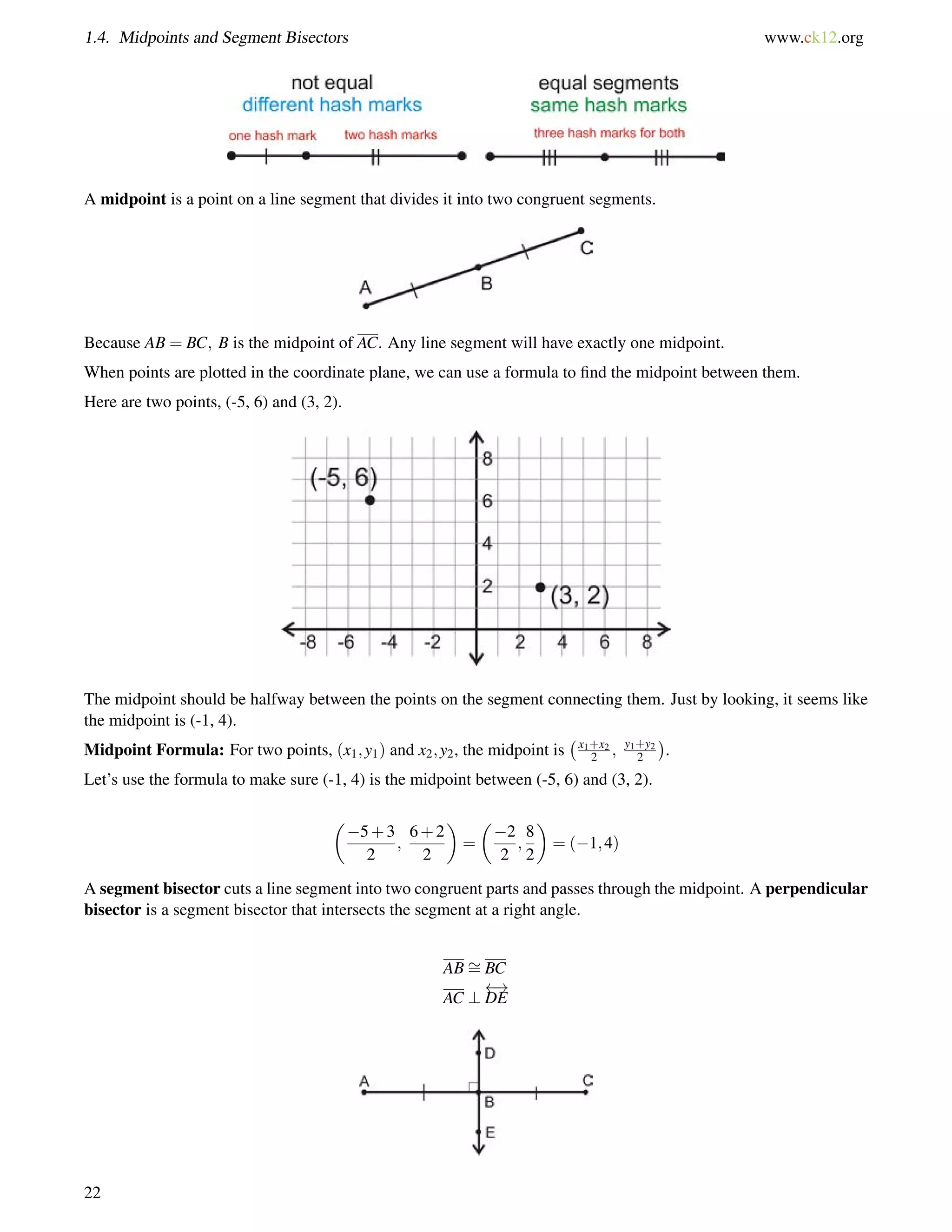
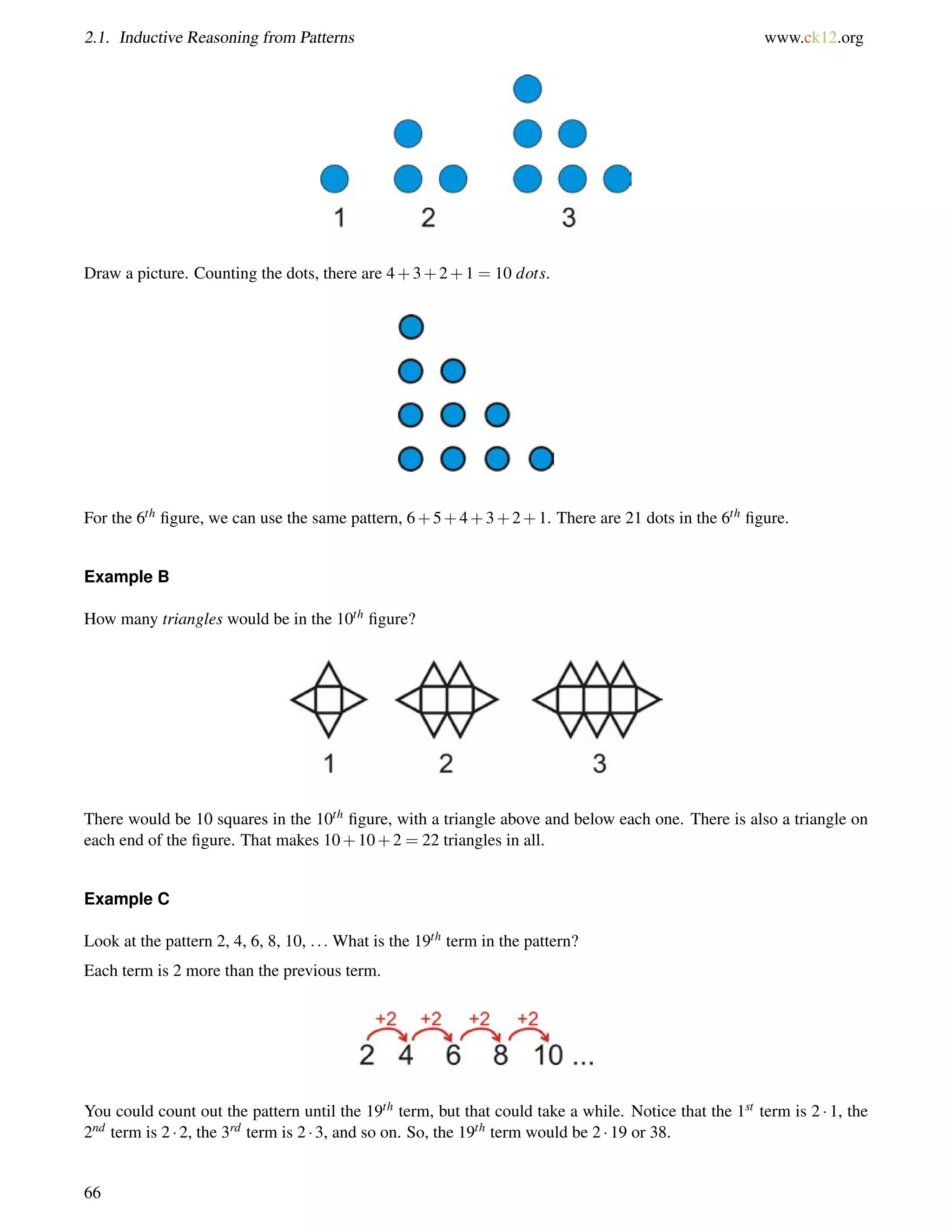
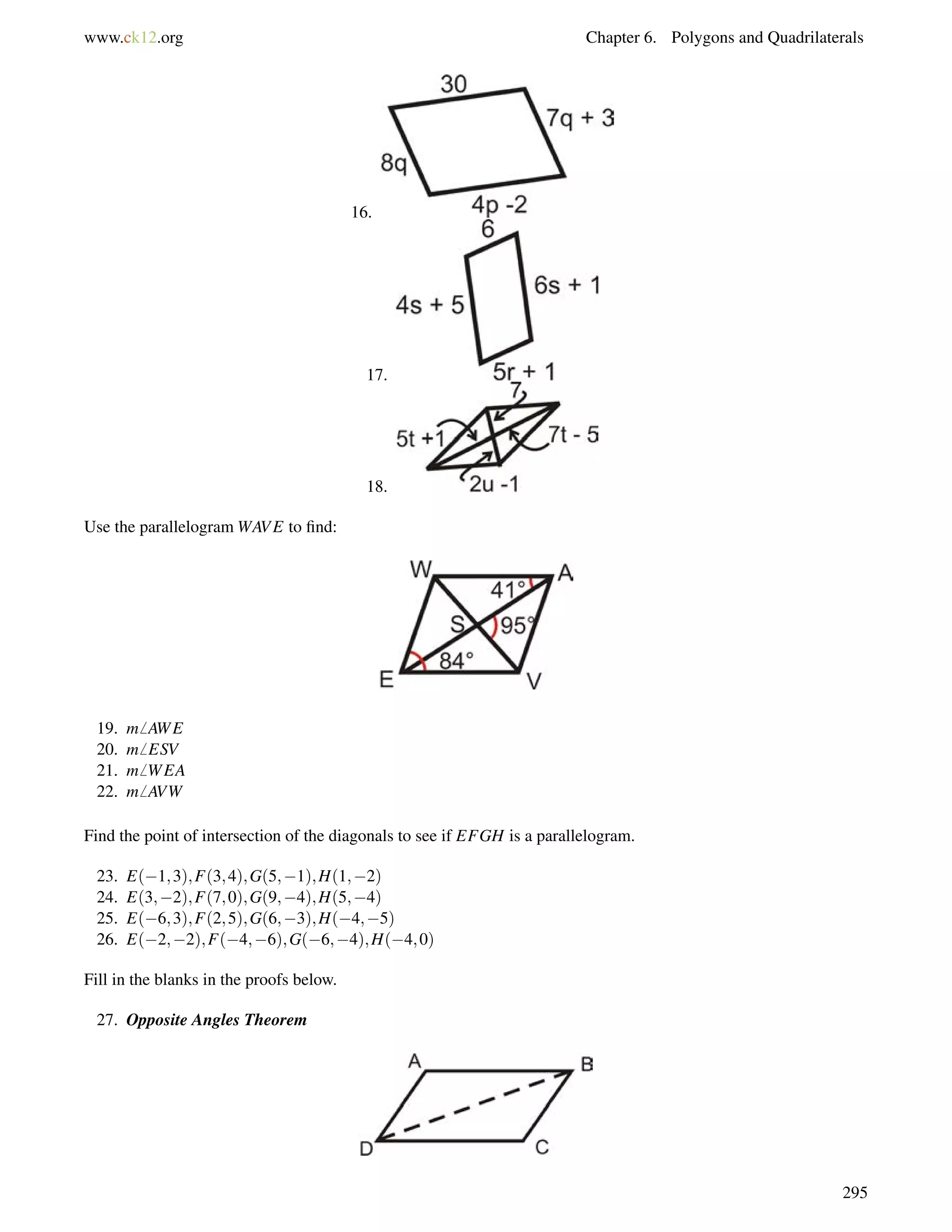
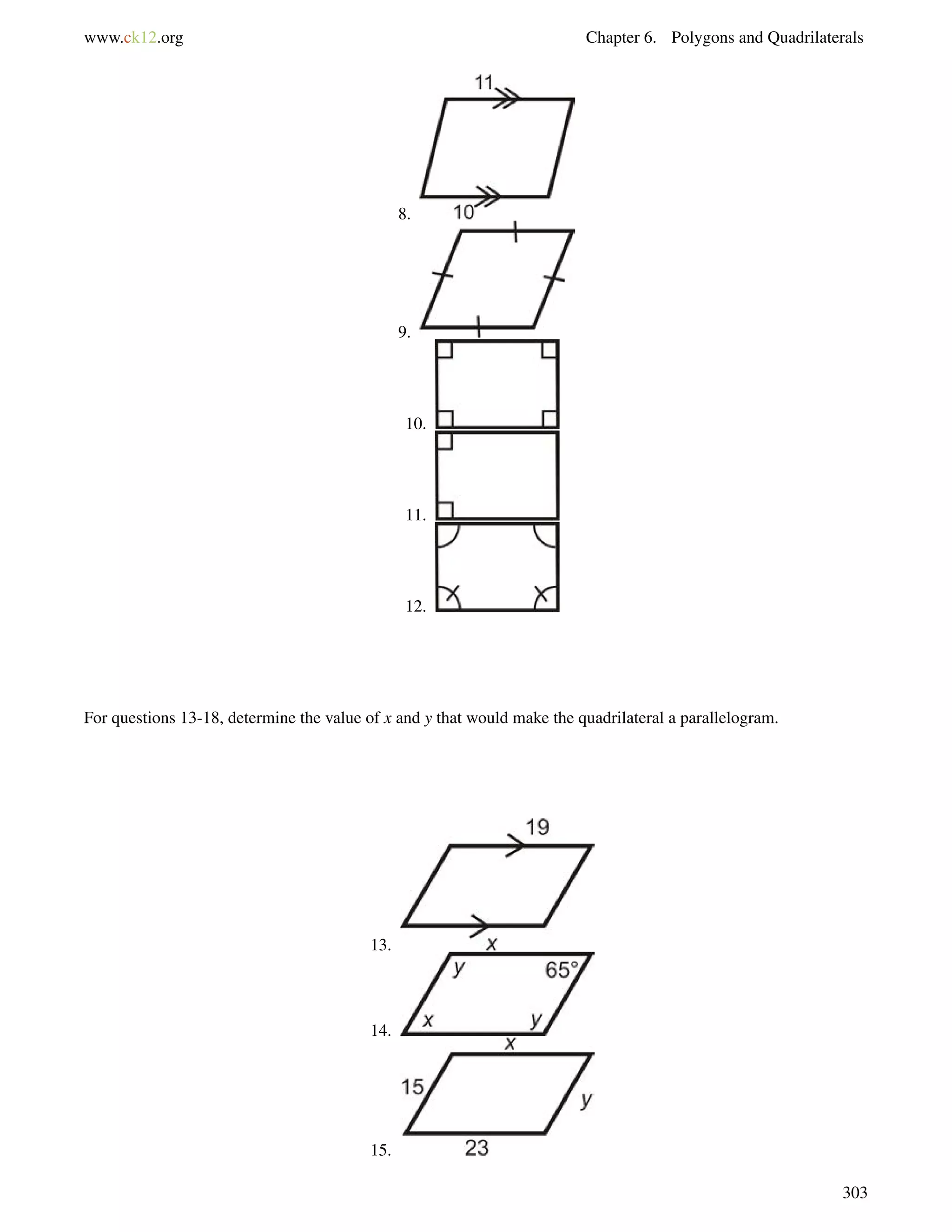
![4.1. Triangle Sum Theorem www.ck12.org
Guided Practice
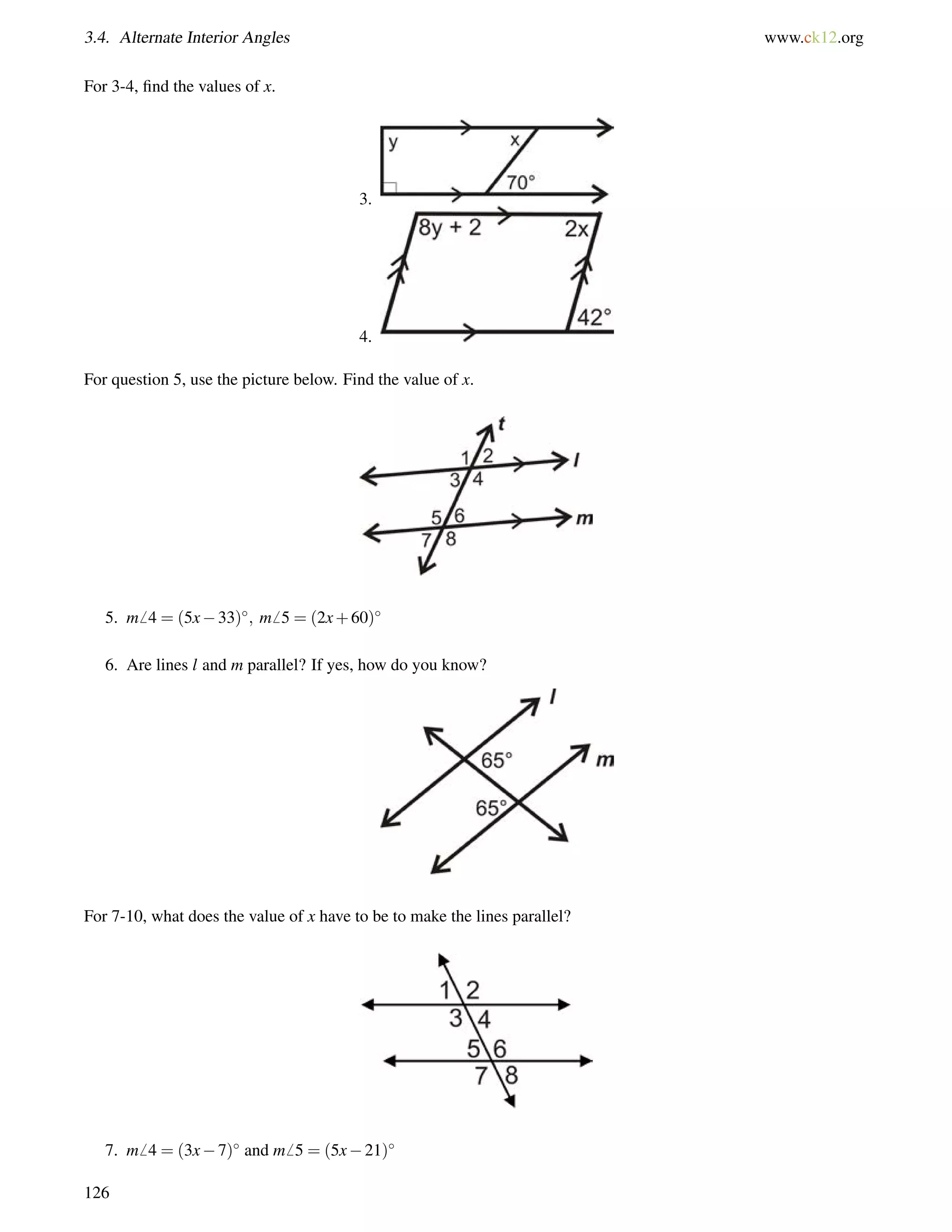
1. Determine m6 1 in this triangle:
2. Two interior angles of a triangle measure 50 and 70. What is the third interior angle of the triangle?
3. Find the value of x and the measure of each angle.
Answers:
1. 72+65+m6 1 = 180.
Solve this equation and you find that m6 1 = 43.
2. 50+70+x = 180.
Solve this equation and you find that the third angle is 60.
3. All the angles add up to 180.
(8x1)+(3x+9)+(3x+4) = 180
(14x+12) = 180
14x = 168
x = 12
Substitute in 12 for x to find each angle.
[3(12)+9] = 45 [3(12)+4] = 40 [8(12)1] = 95
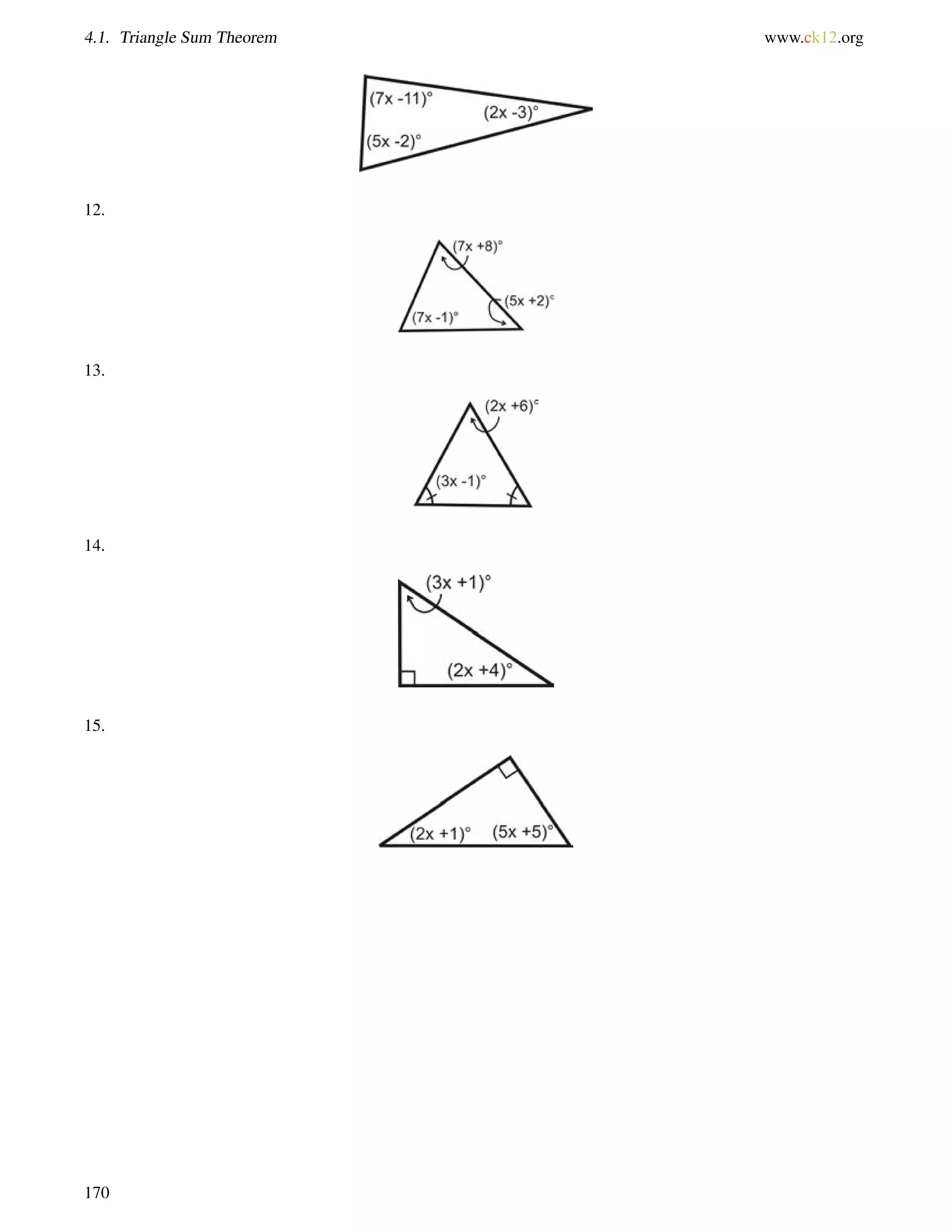
Practice
Determine m6 1 in each triangle.
1.
168](https://image.slidesharecdn.com/ck-12-basic-geometry-conceptsbv10tfrs1reduced-141002074324-phpapp01/75/Ck-12-basic-geometry-concepts-174-2048.jpg)





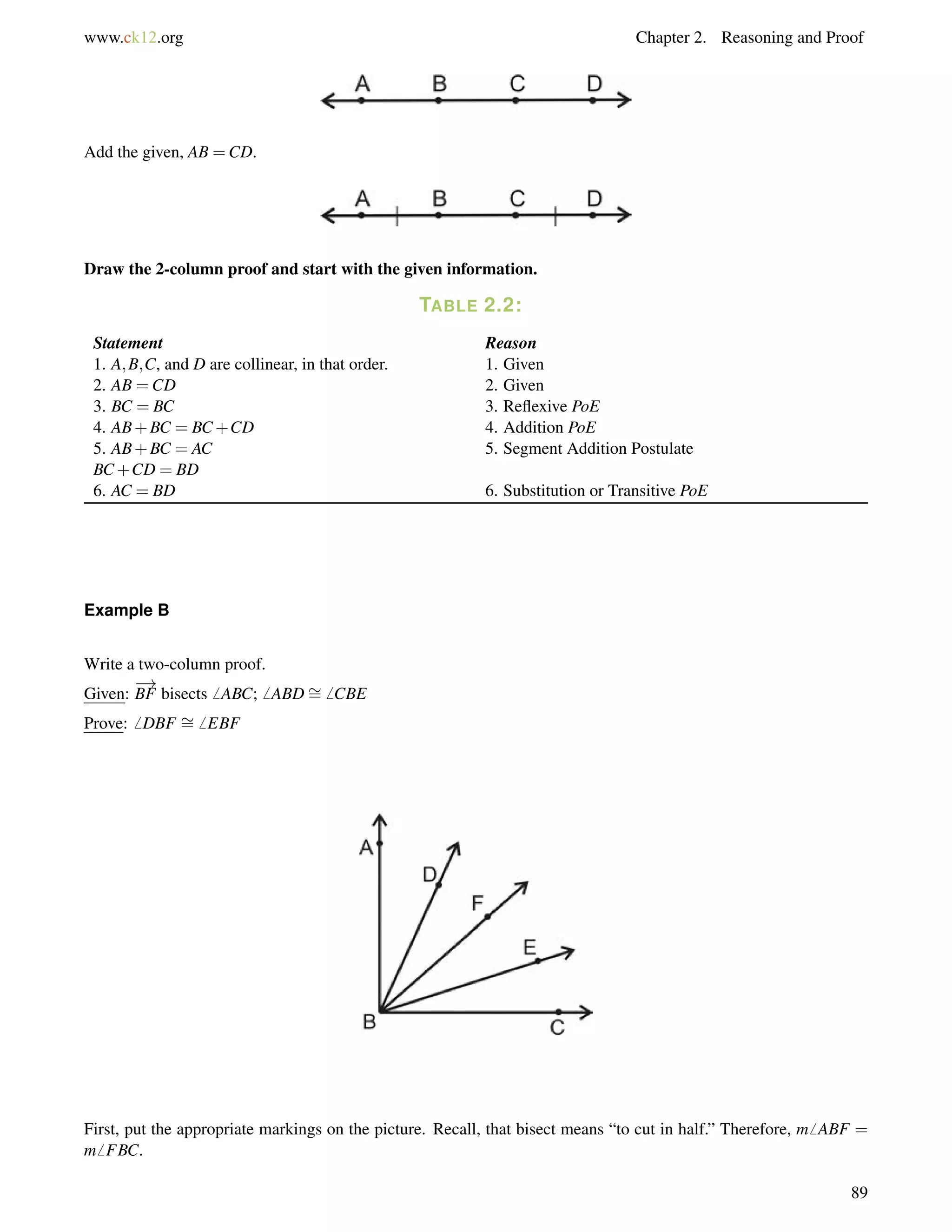
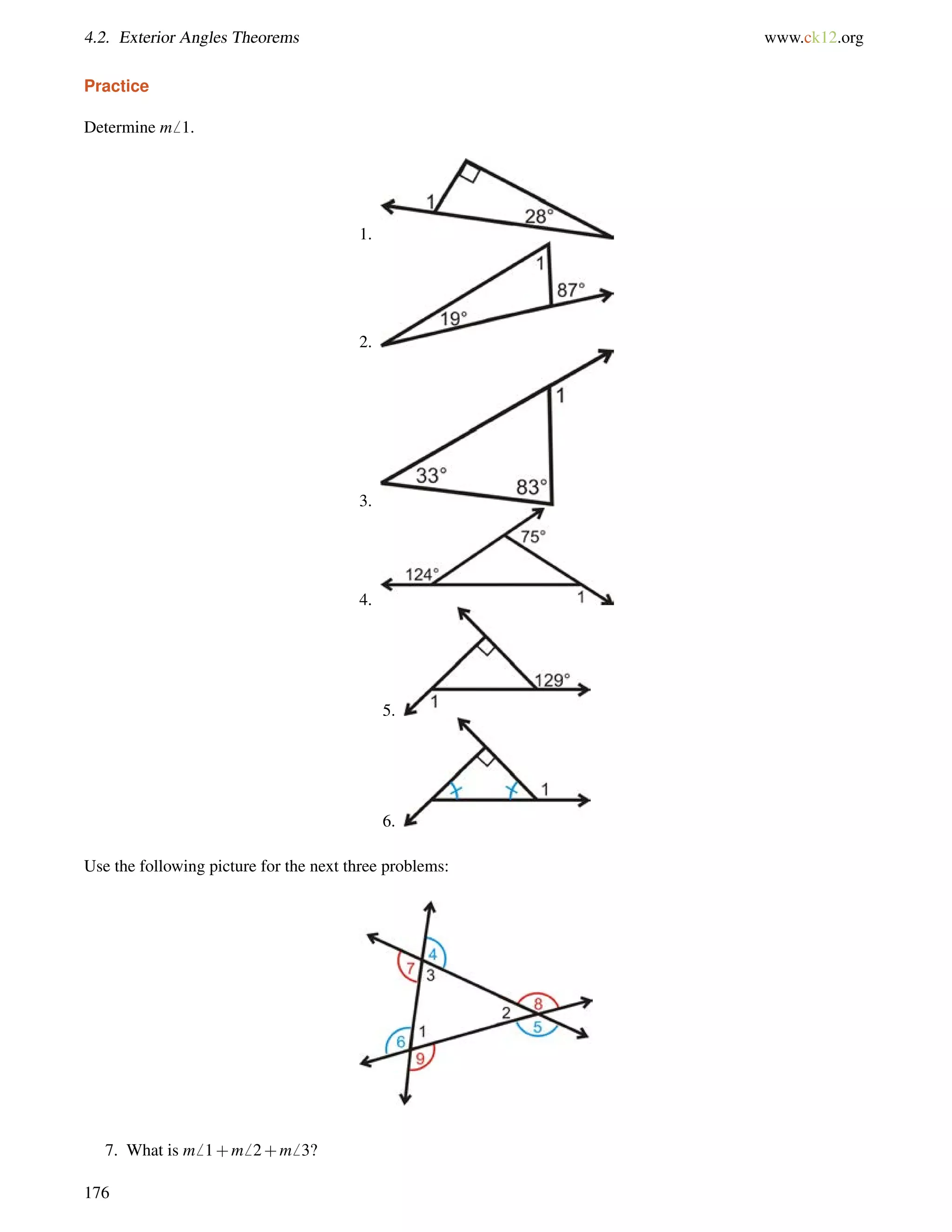
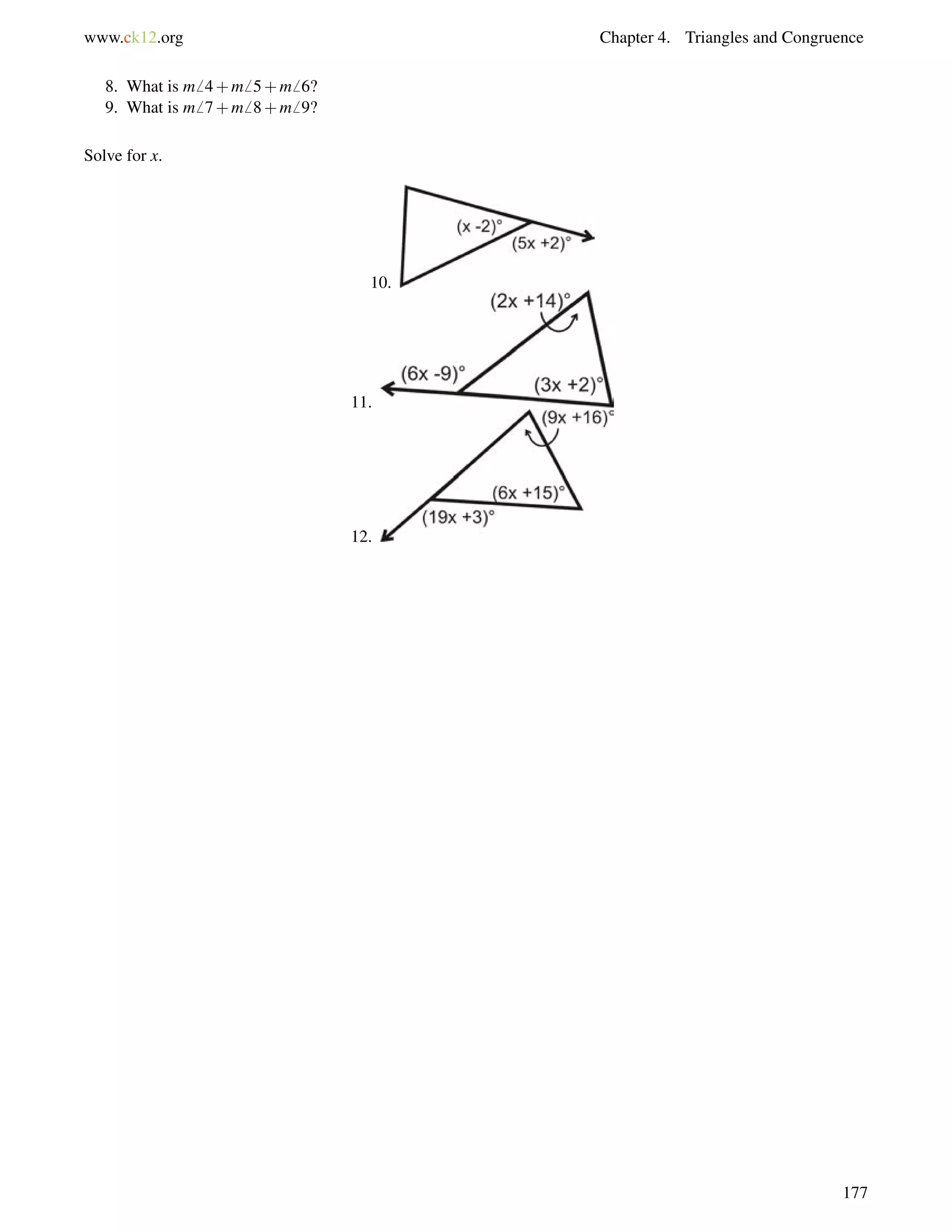
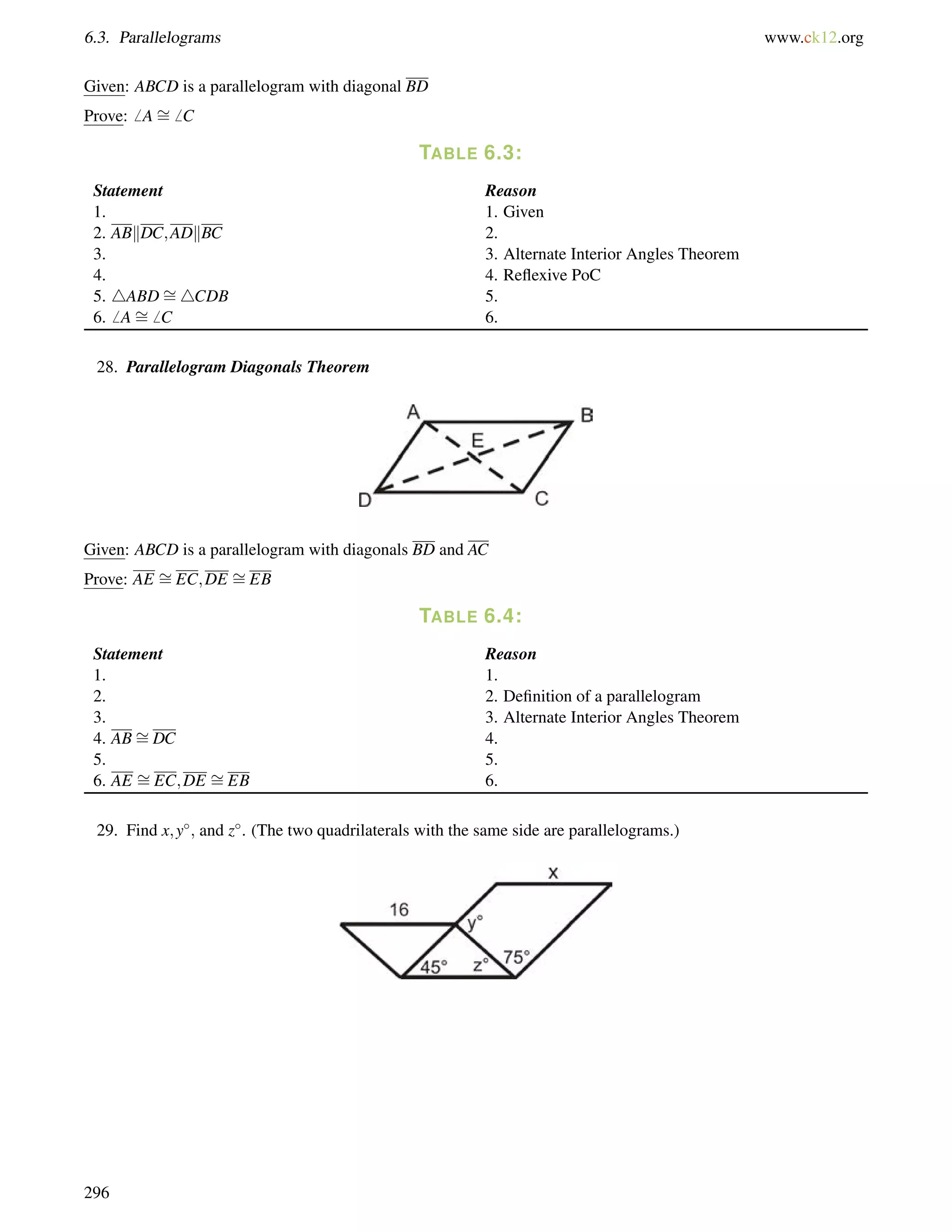
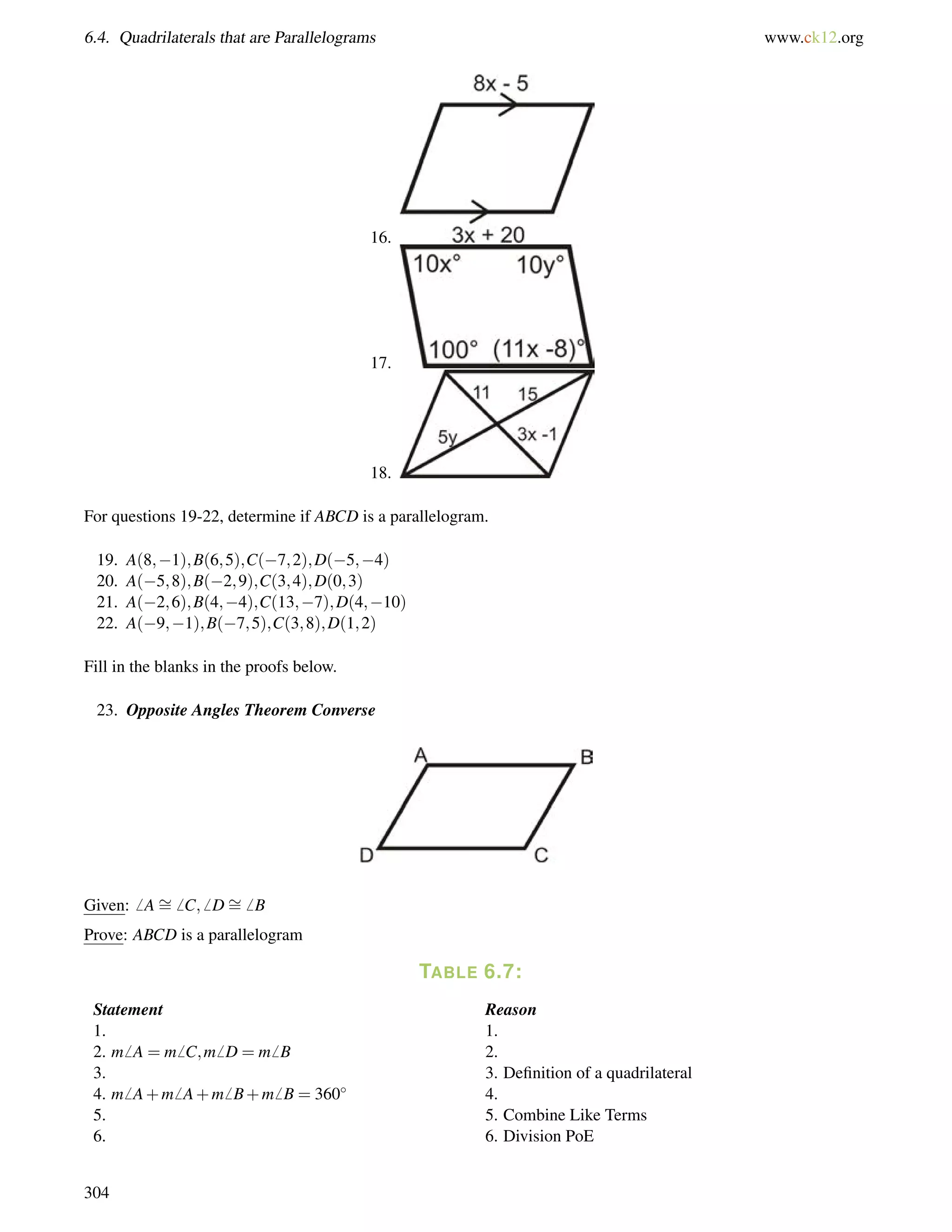
![www.ck12.org Chapter 4. Triangles and Congruence
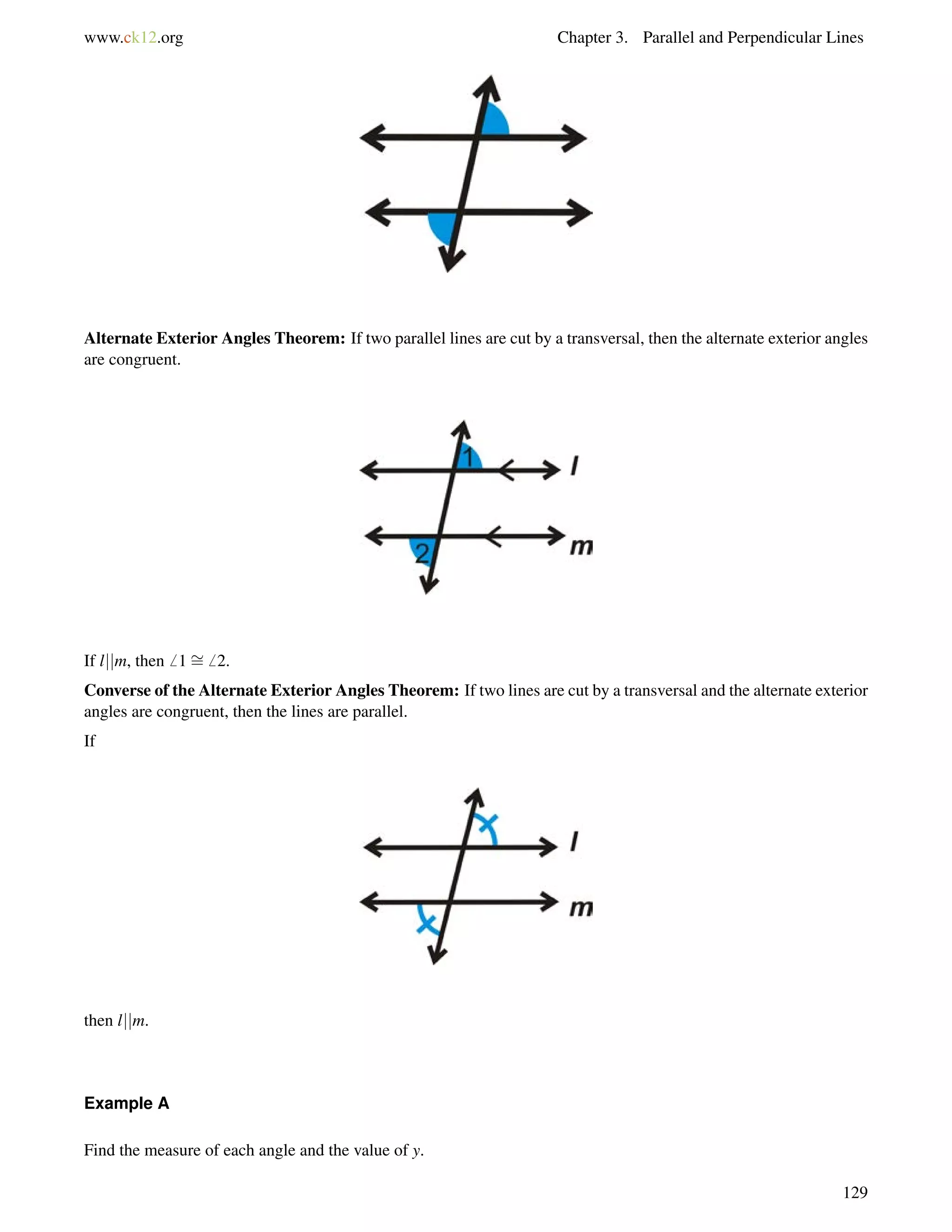
2. Two interior angles of a triangle are 40 and 73. What are the measures of the three exterior angles of the
triangle?
3. Find the value of x and the measure of each angle.
Answers:
1. Using the Exterior Angle Theorem
m6 C+16 = 121
m6 C = 105
If you forget the Exterior Angle Theorem, you can do this problem just like Example C.
2. Remember that every interior angle forms a linear pair (adds up to 180) with an exterior angle. So, since one
of the interior angles is 40 that means that one of the exterior angles is 140 (because 40+140 = 180). Similarly,
since another one of the interior angles is 73, one of the exterior angles must be 107. The third interior angle is
not given to us, but we could figure it out using the Triangle Sum Theorem. We can also use the Exterior Angle
Sum Theorem. If two of the exterior angles are 140 and 107, then the third Exterior Angle must be 113 since
140+107+113 = 360.
So, the measures of the three exterior angles are 140, 107 and 113.
3. Set up an equation using the Exterior Angle Theorem.
(4x+2)+(2x9) = (5x+13)
%
remote interior angles exterior angle
(6x7) = (5x+13)
x = 20
Substitute in 20 for x to find each angle.
[4(20)+2] = 82 [2(20)9] = 31 Exterior angle: [5(20)+13] = 113
175](https://image.slidesharecdn.com/ck-12-basic-geometry-conceptsbv10tfrs1reduced-141002074324-phpapp01/75/Ck-12-basic-geometry-concepts-181-2048.jpg)










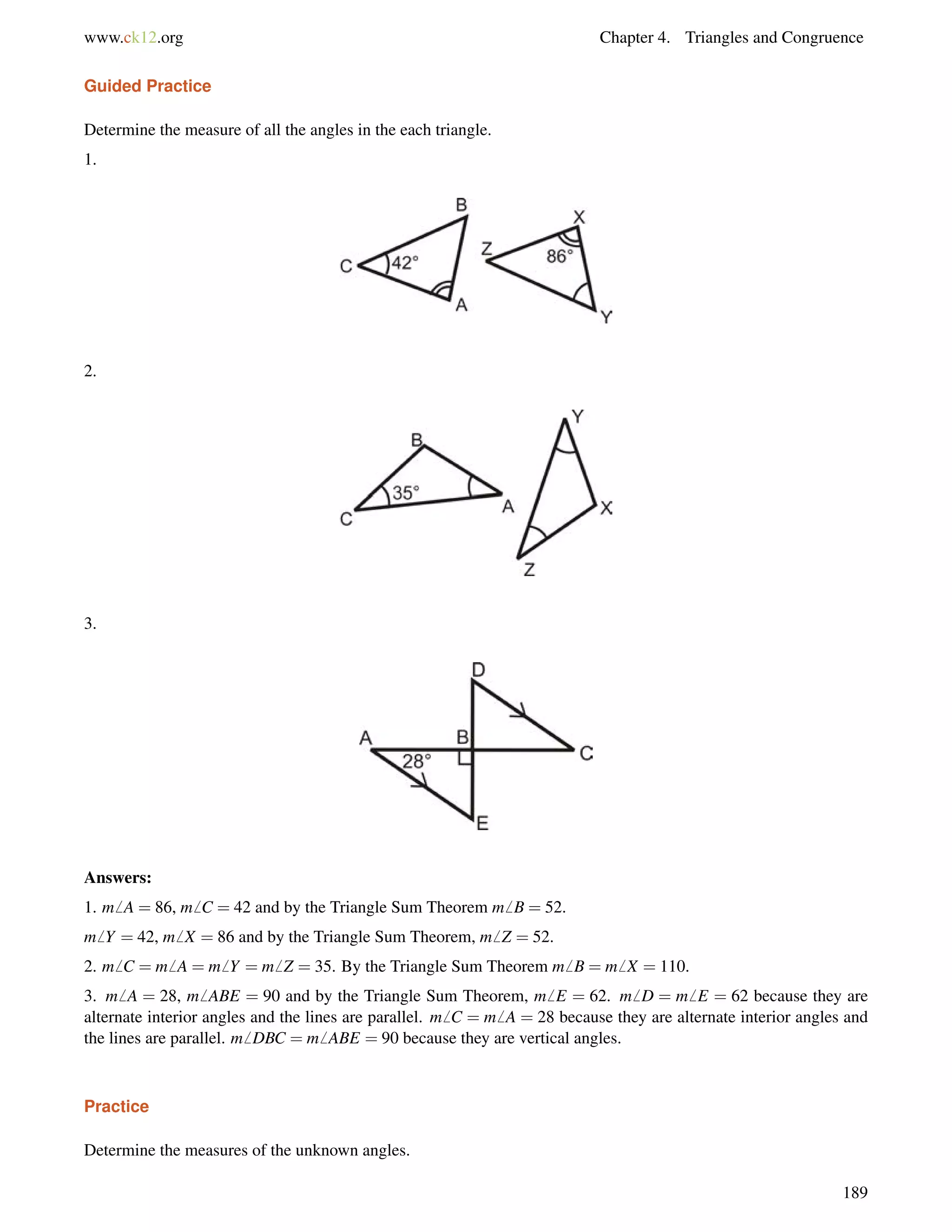
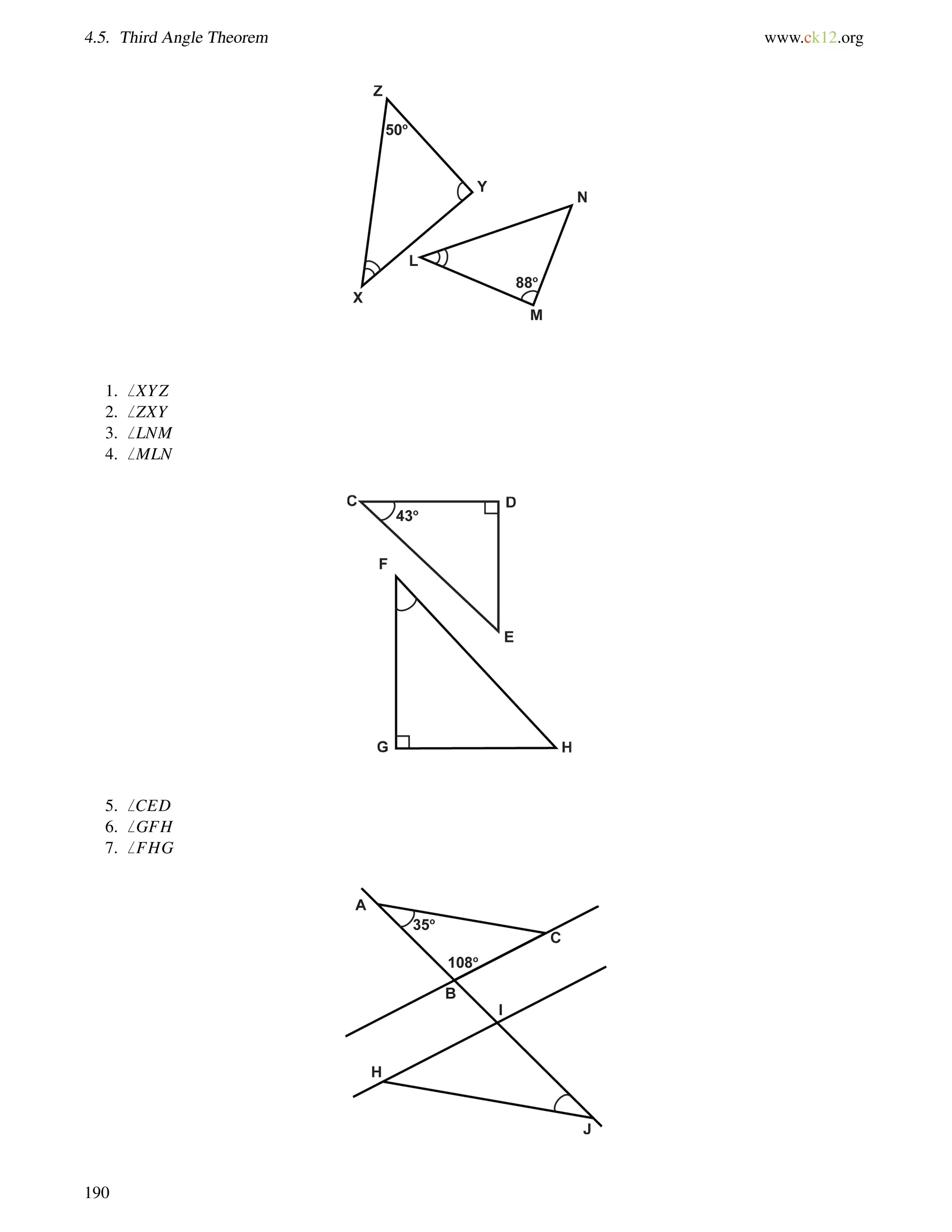
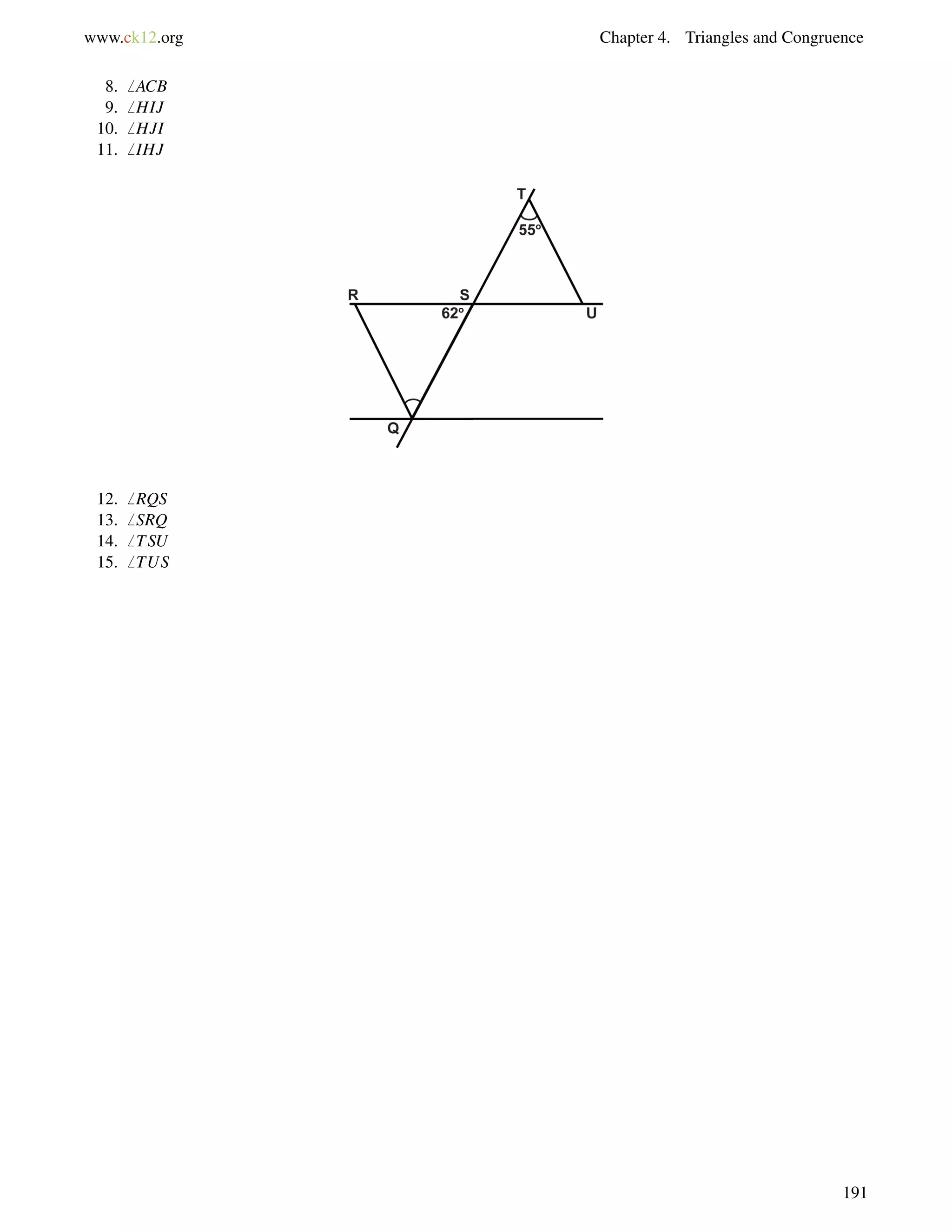




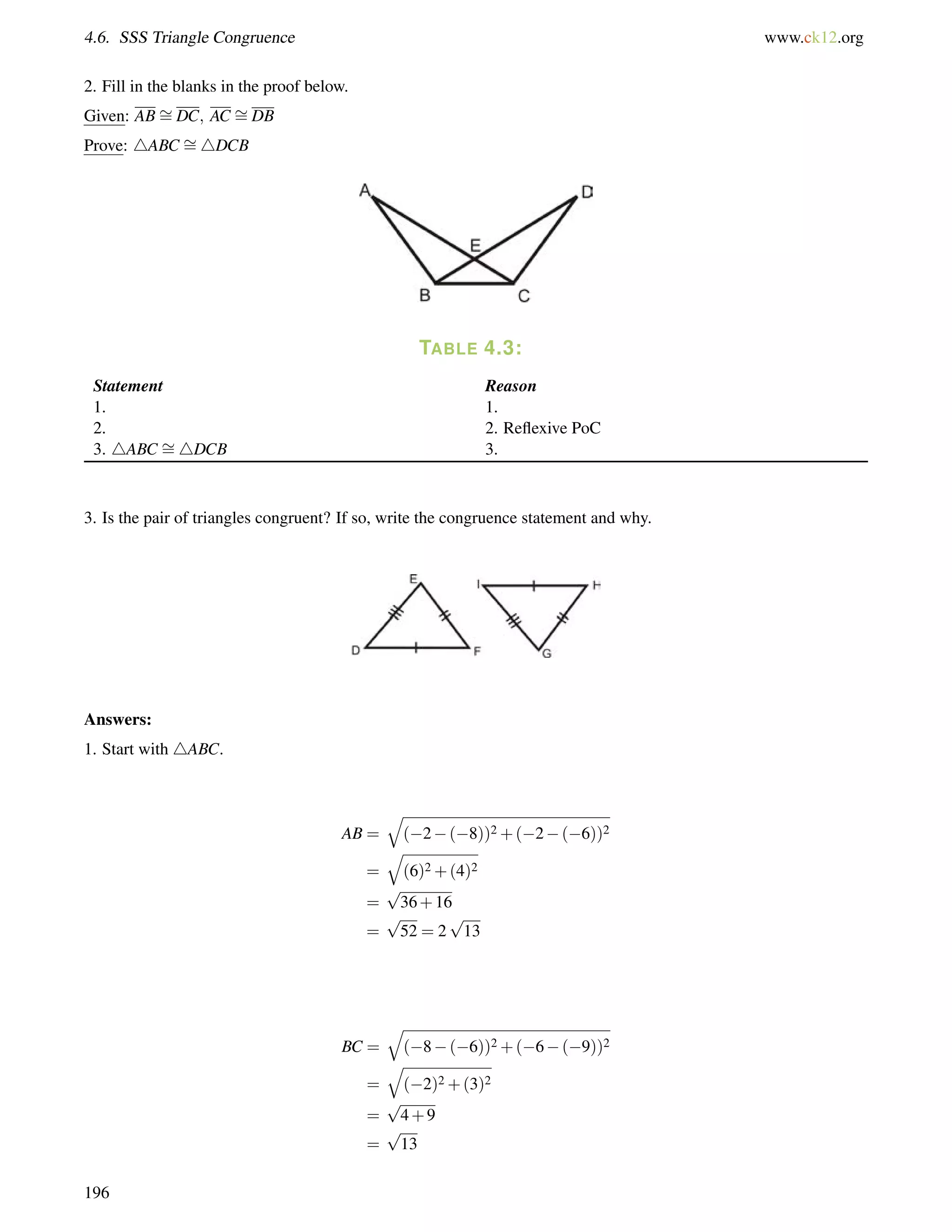

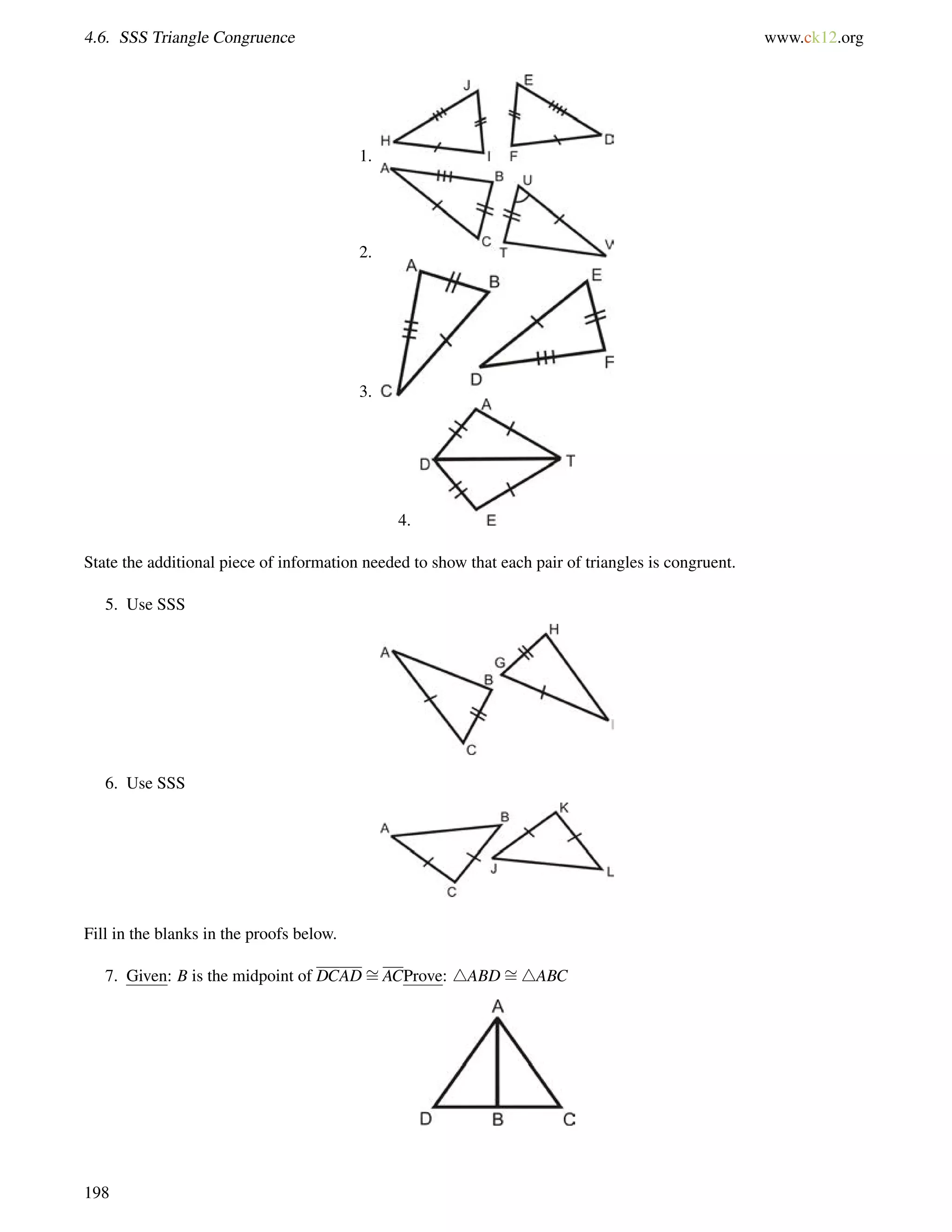
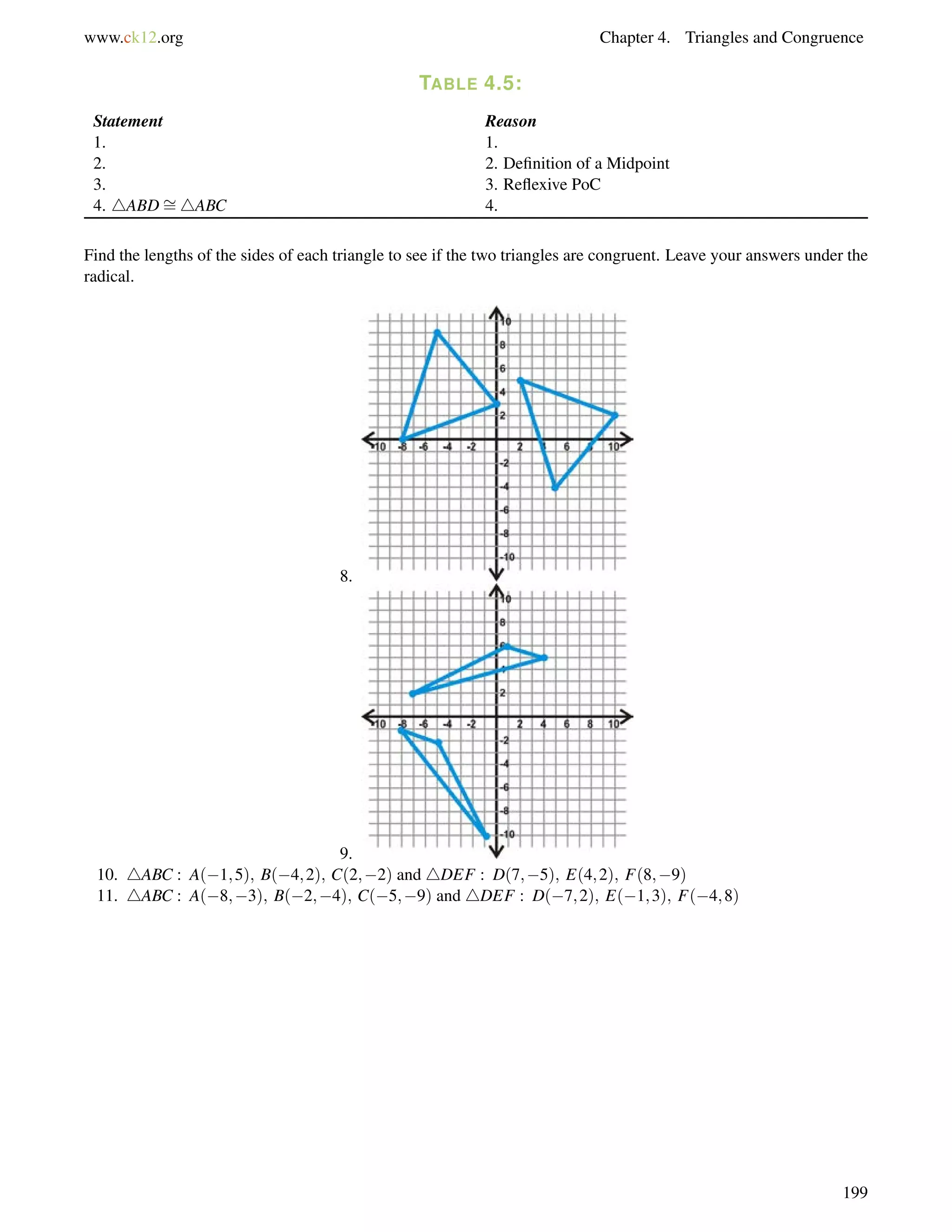



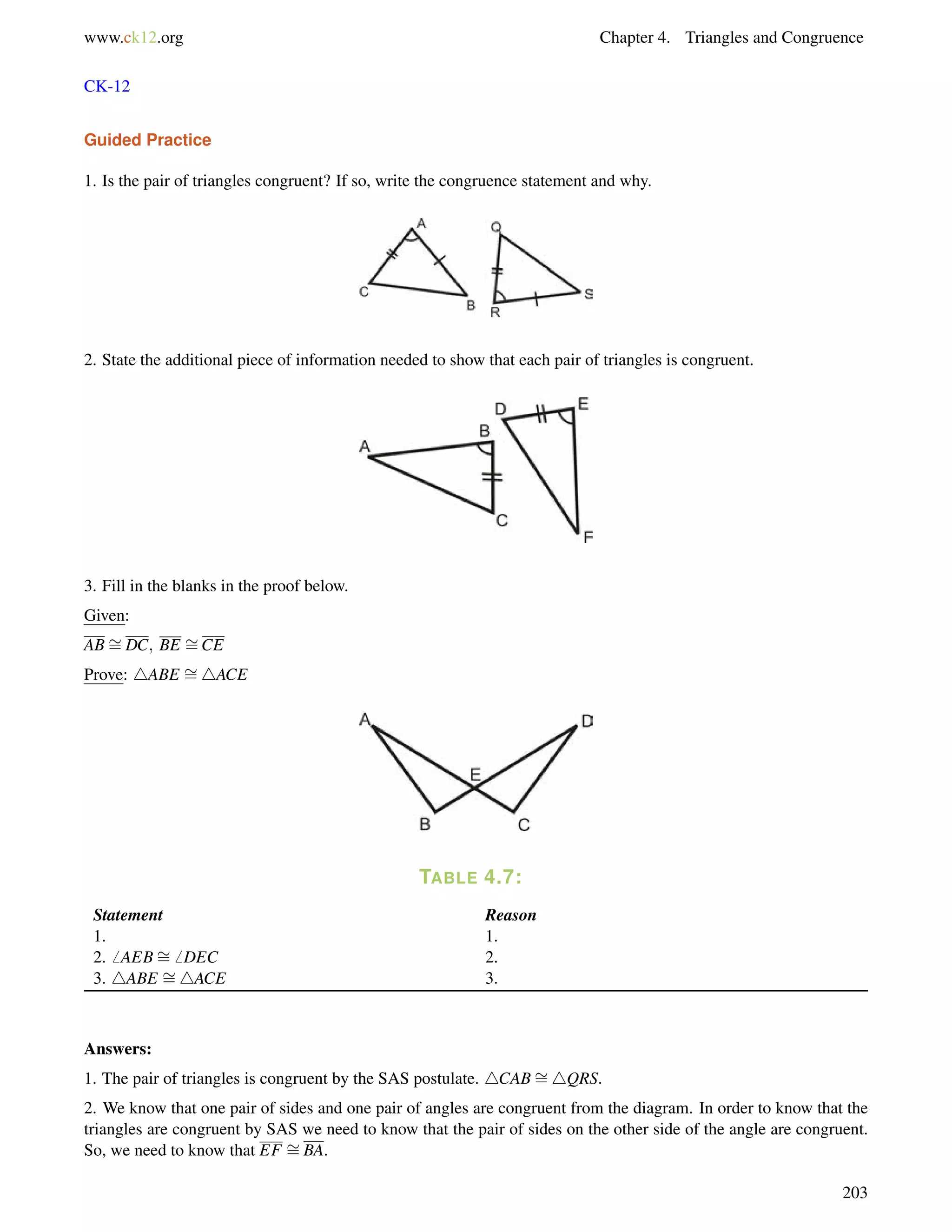

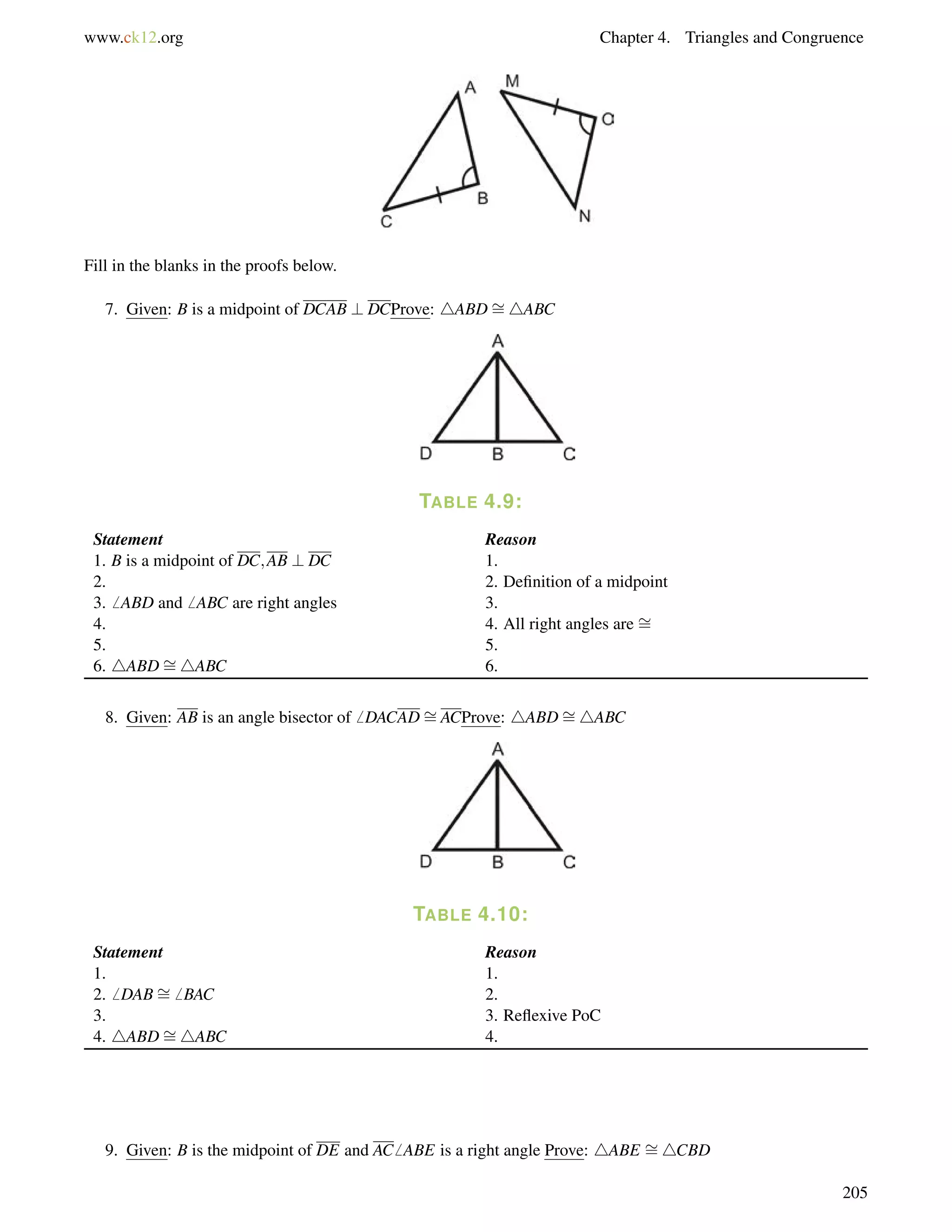
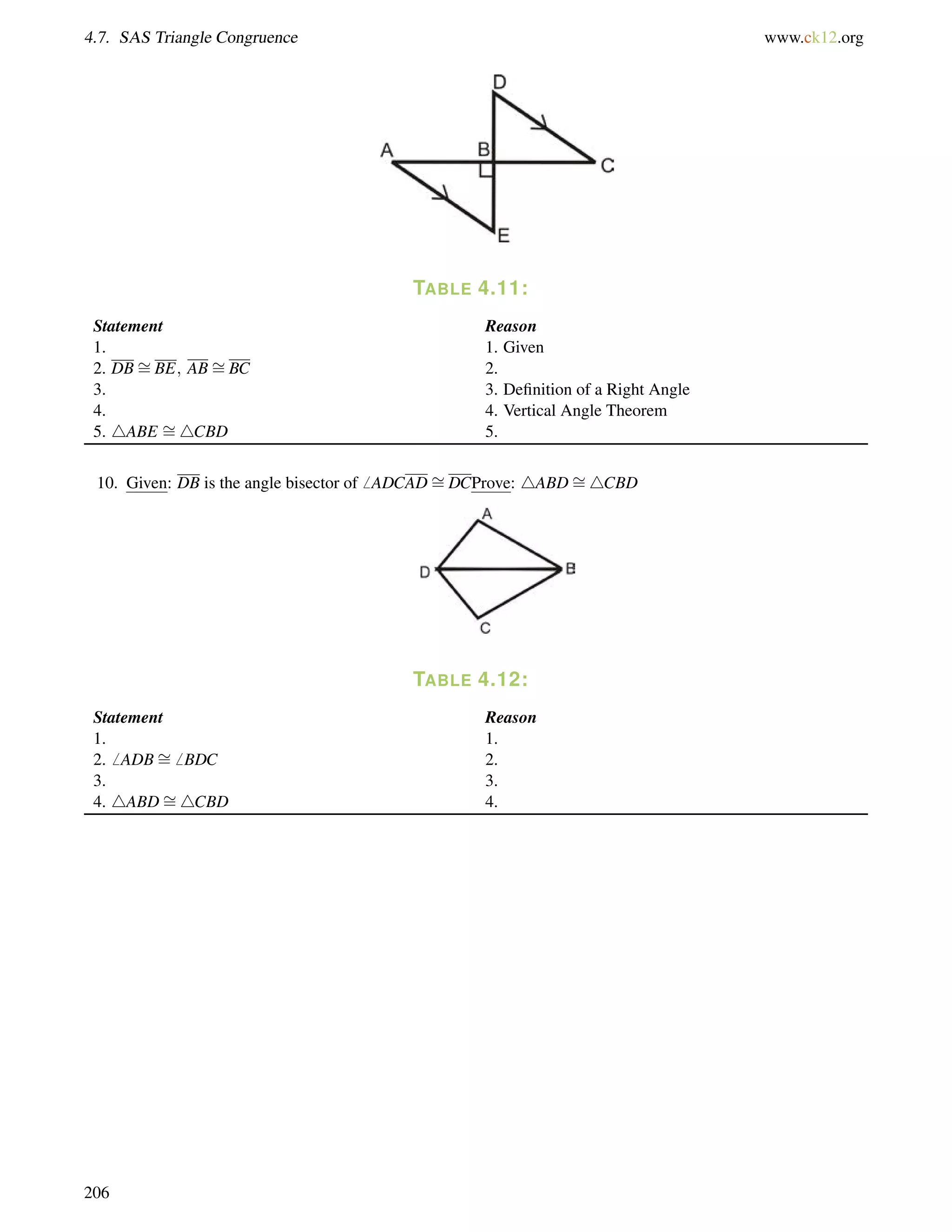






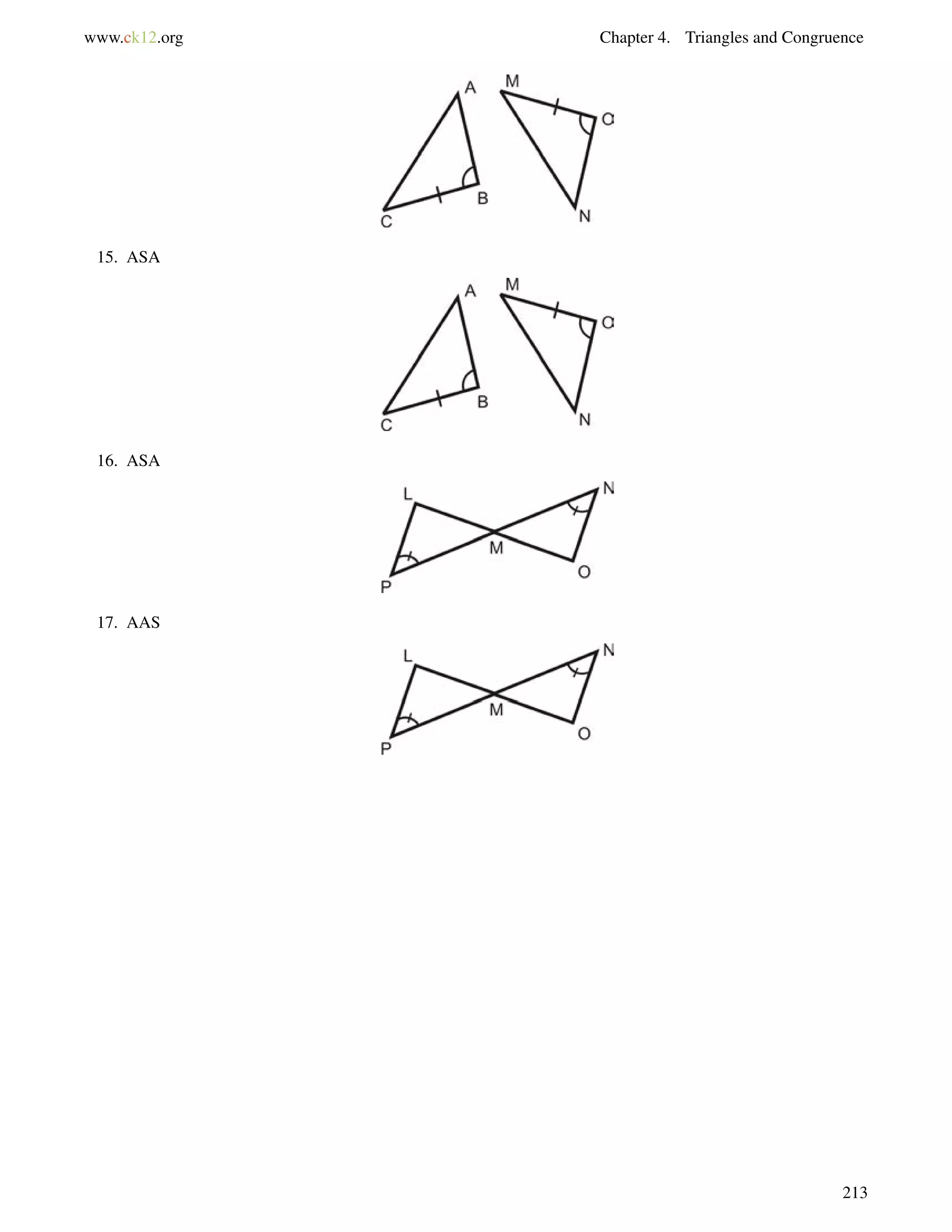








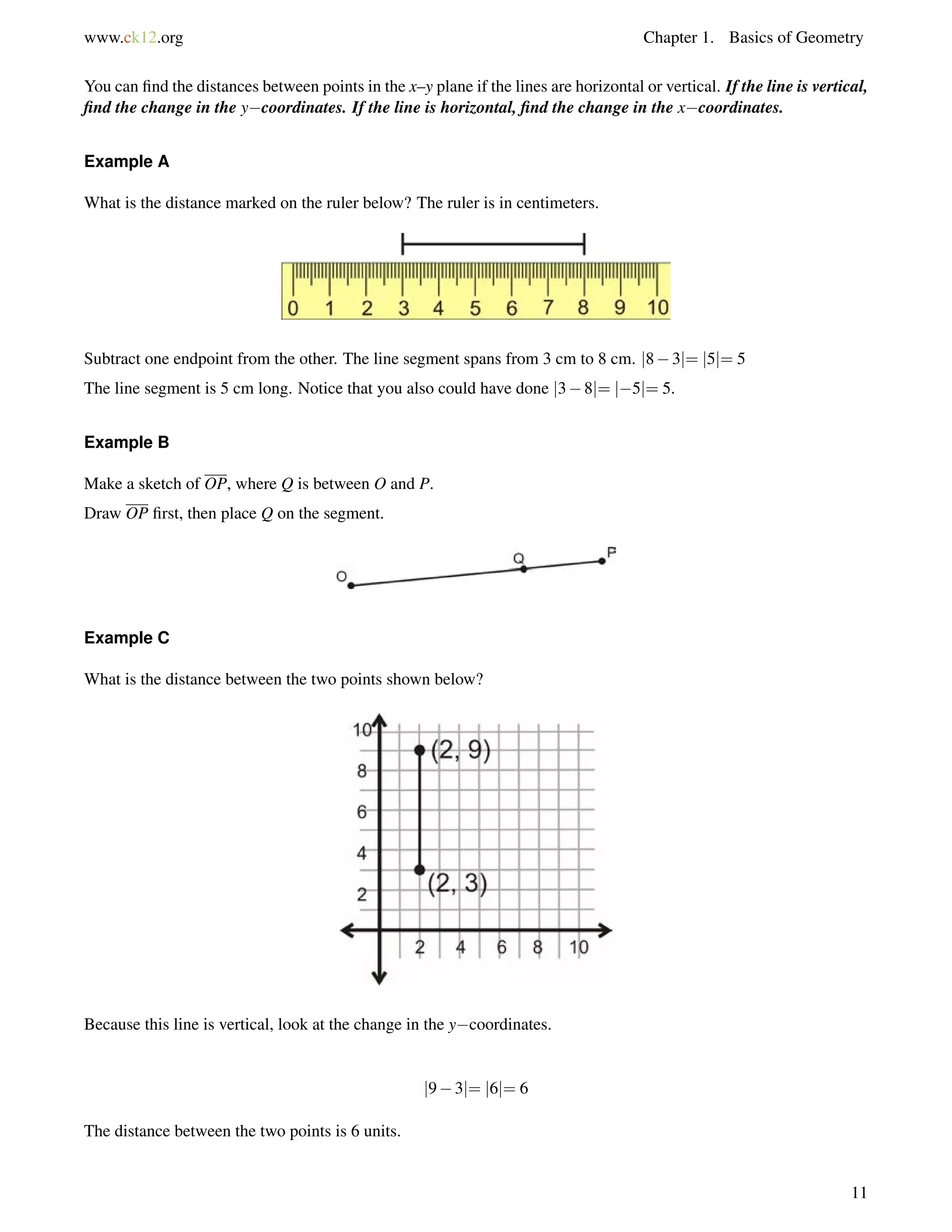
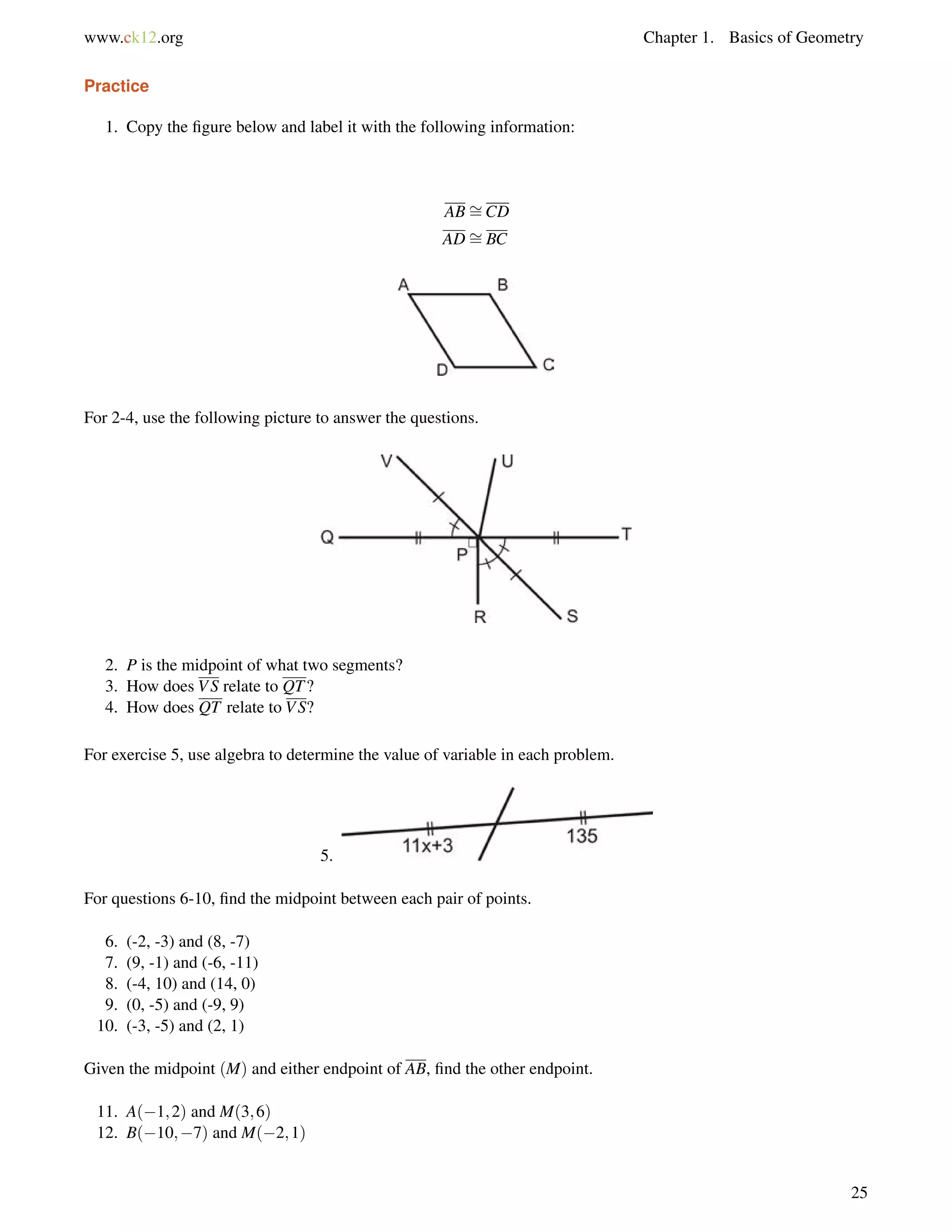
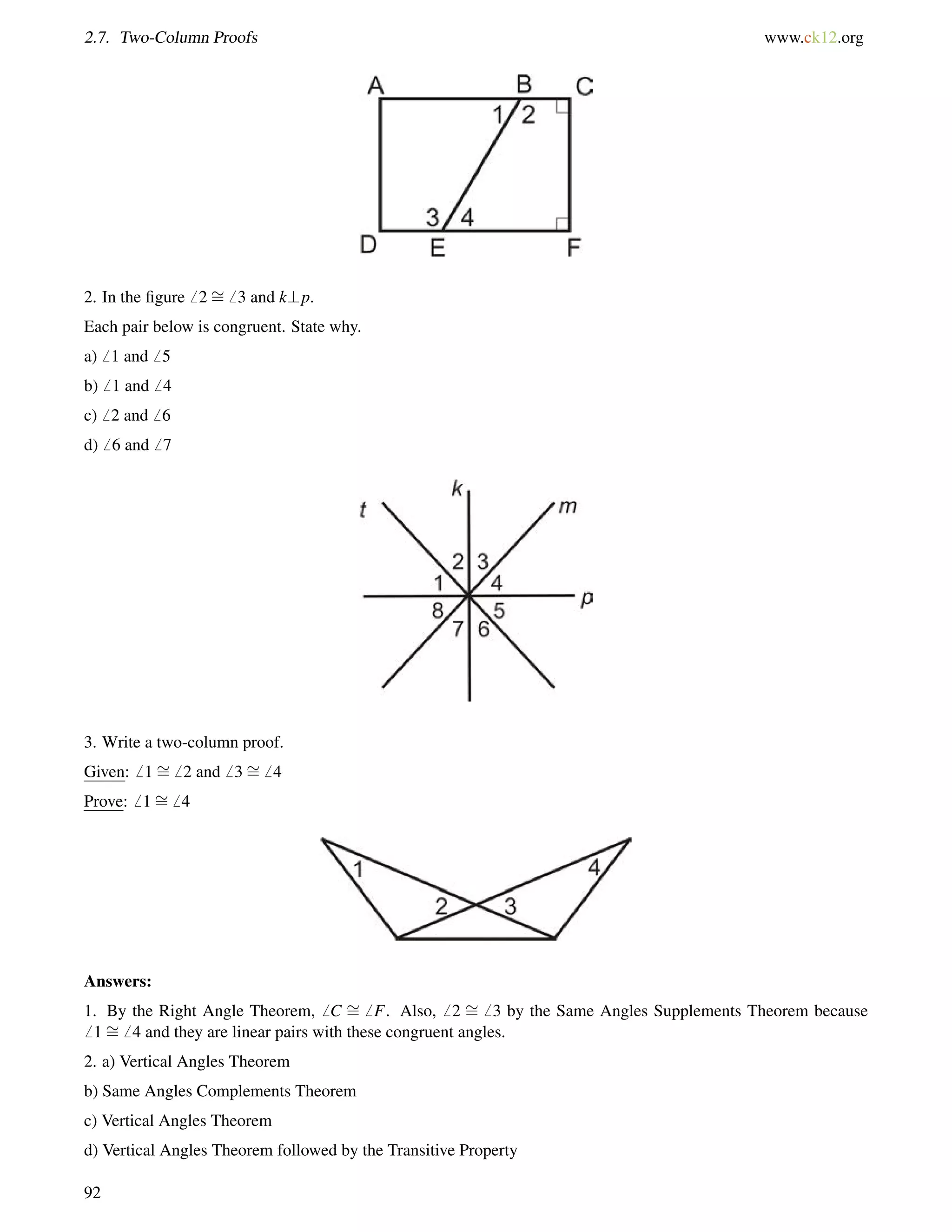
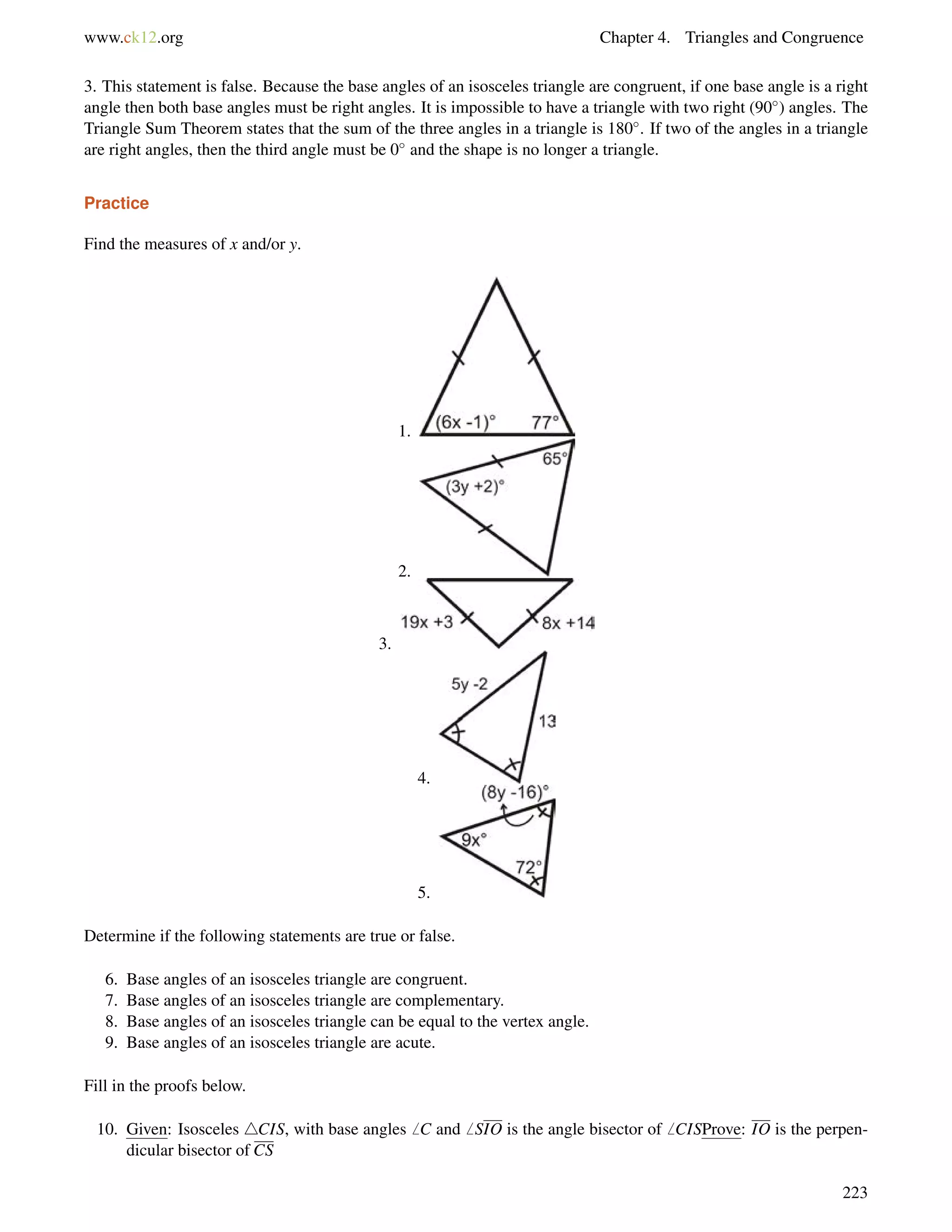
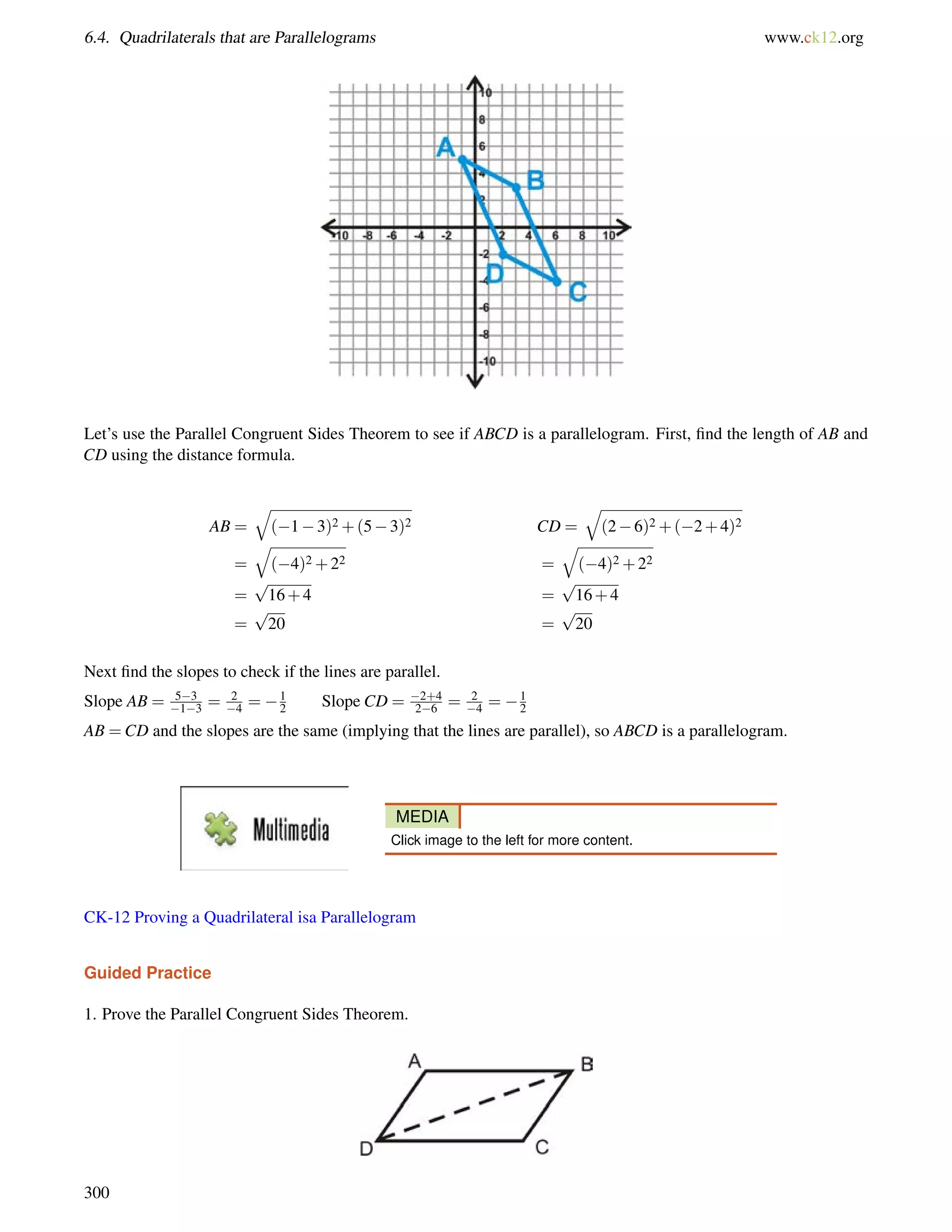
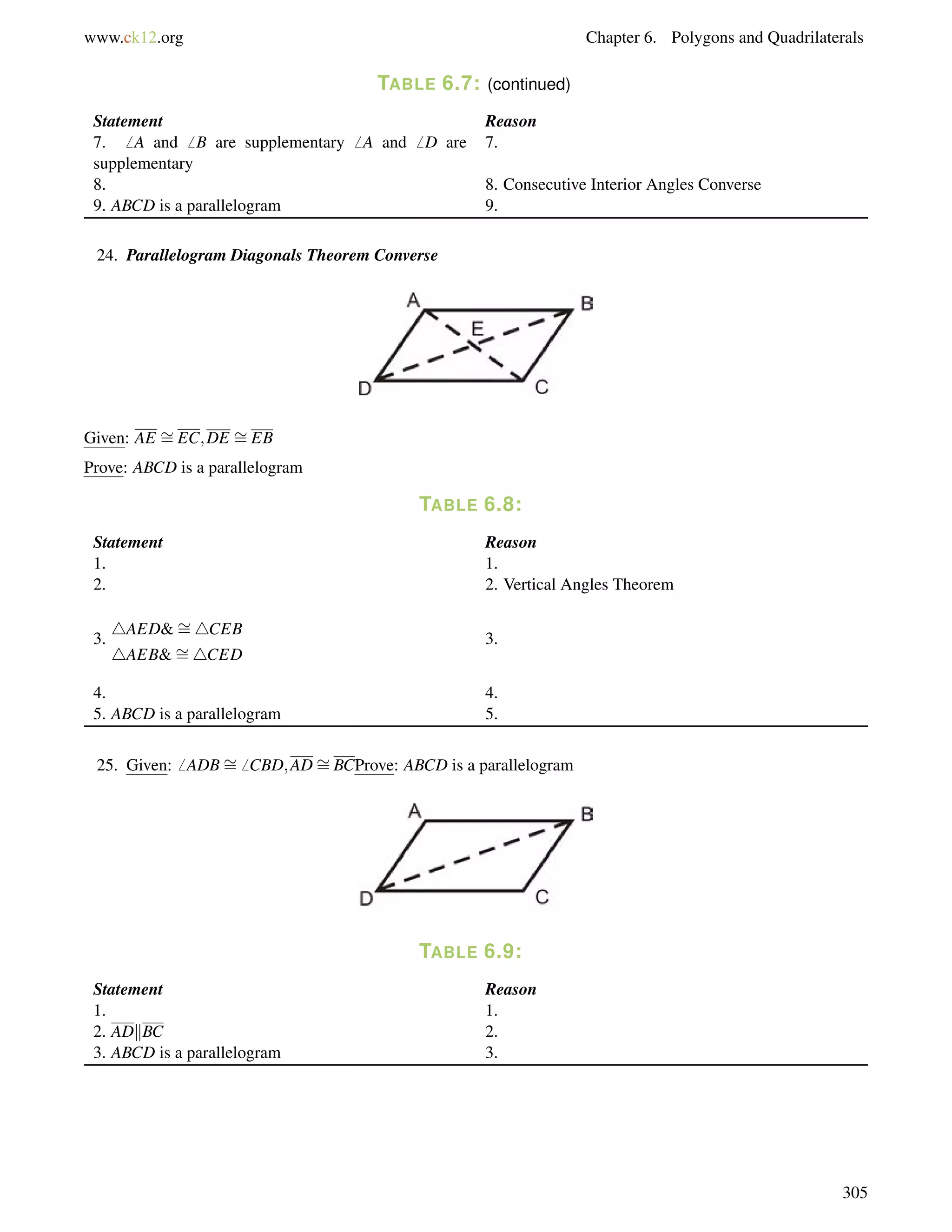
![4.10. Isosceles Triangles www.ck12.org
Draw a picture and set up and equation to solve for the base angles, b.
116+b+b = 180
2b = 64
b = 32
MEDIA
Click image to the left for more content.
CK-12 Isosceles Triangles
Guided Practice
1. Find the value of xand the measure of each angle.
2. Find the measure of x.
3. True or false: Base angles of an isosceles triangle can be right angles.
Answers:
1. The two angles are equal, so set them equal to each other and solve for x.
(4x+12) = (5x3)
15 = x
Substitute x = 15; the base angles are [4(15)+12], or 72. The vertex angle is 1807272 = 36.
2. The two sides are equal, so set them equal to each other and solve for x.
2x9 = x+5
x = 14
222](https://image.slidesharecdn.com/ck-12-basic-geometry-conceptsbv10tfrs1reduced-141002074324-phpapp01/75/Ck-12-basic-geometry-concepts-228-2048.jpg)



















































































































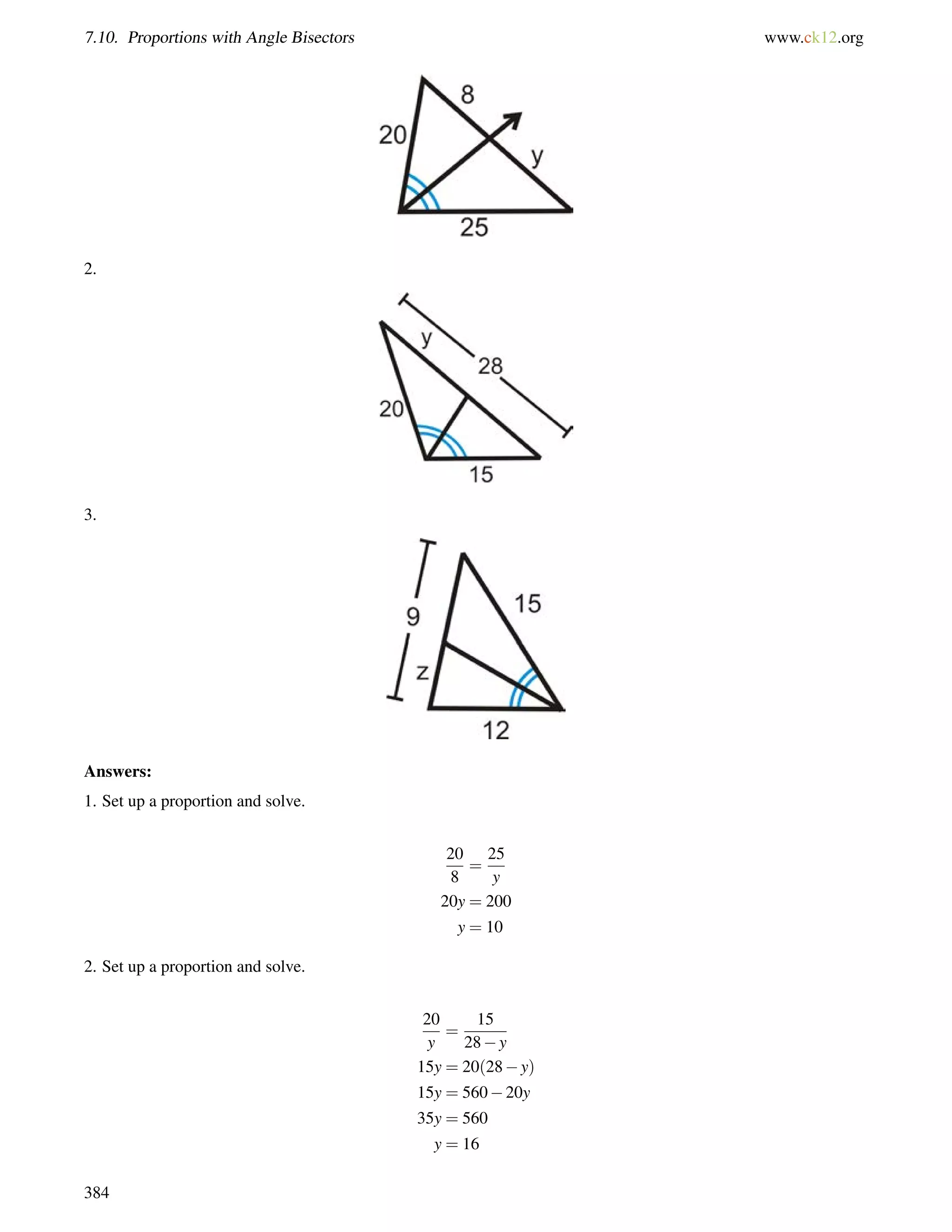
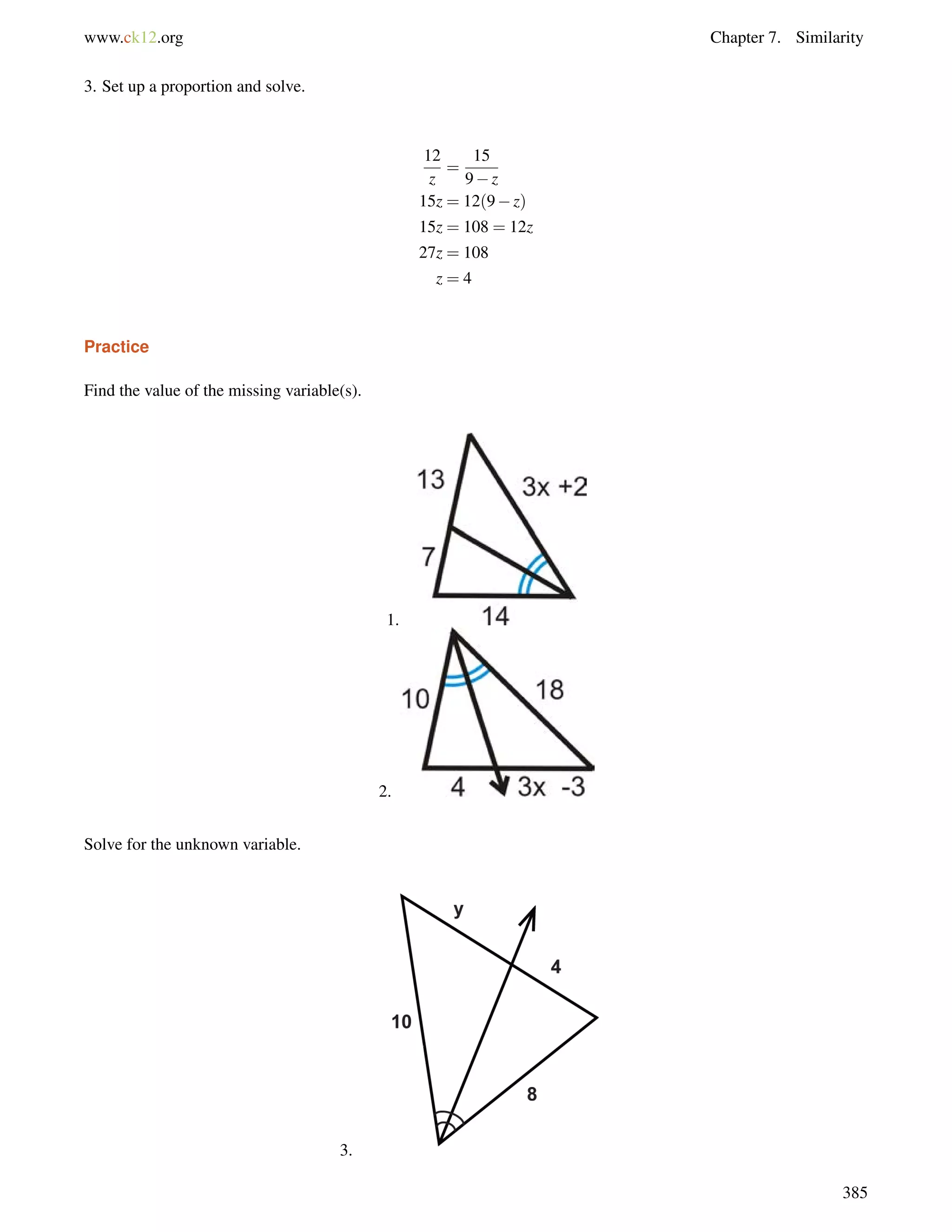
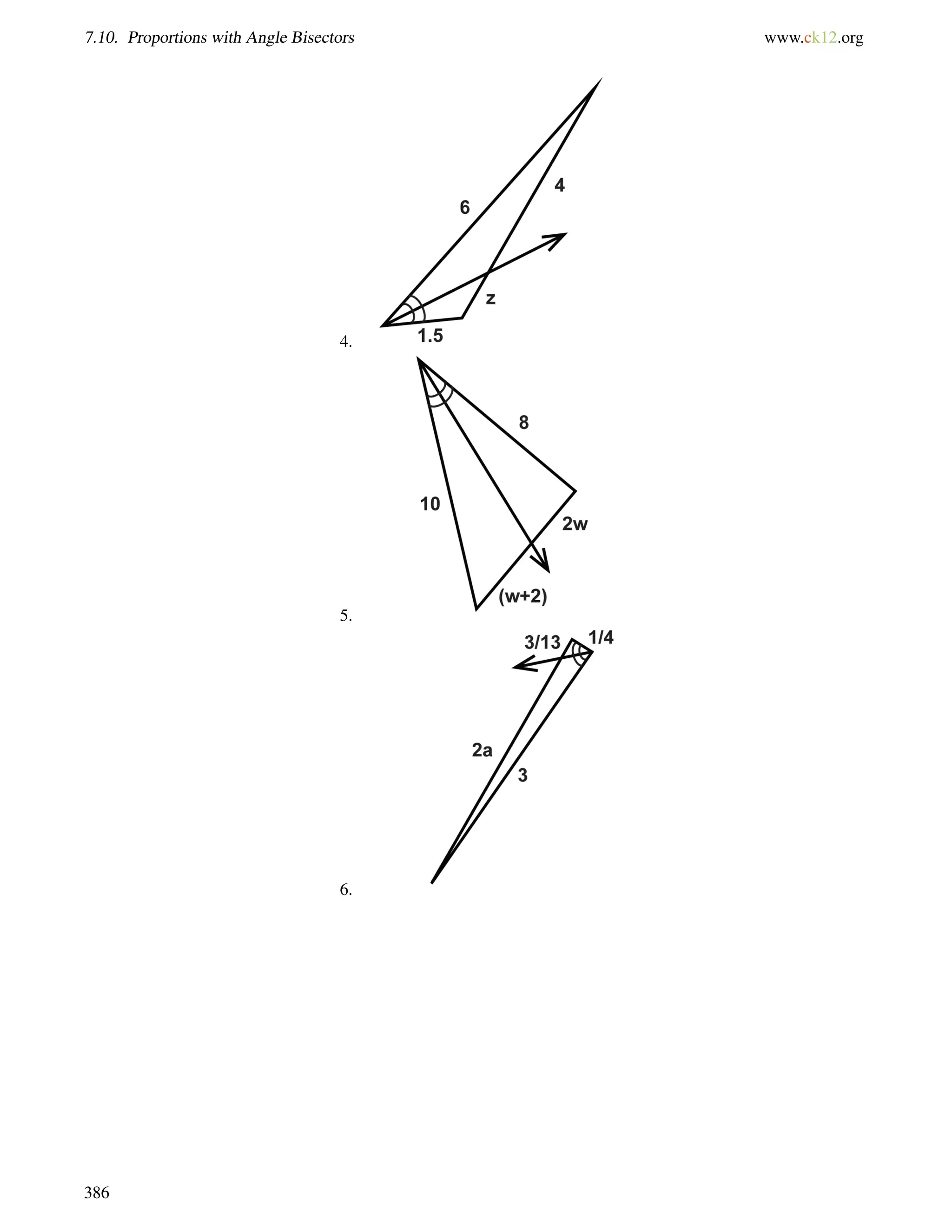
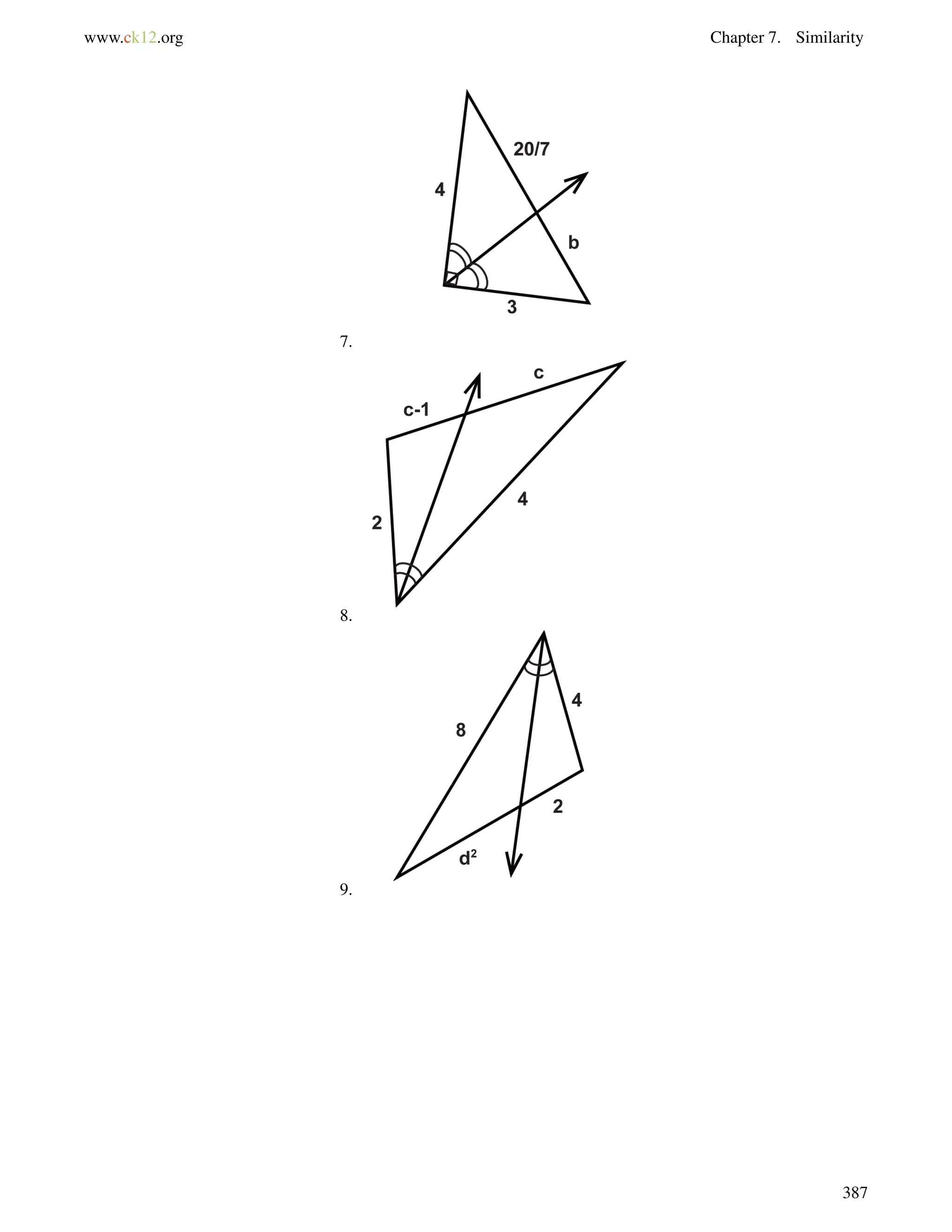






























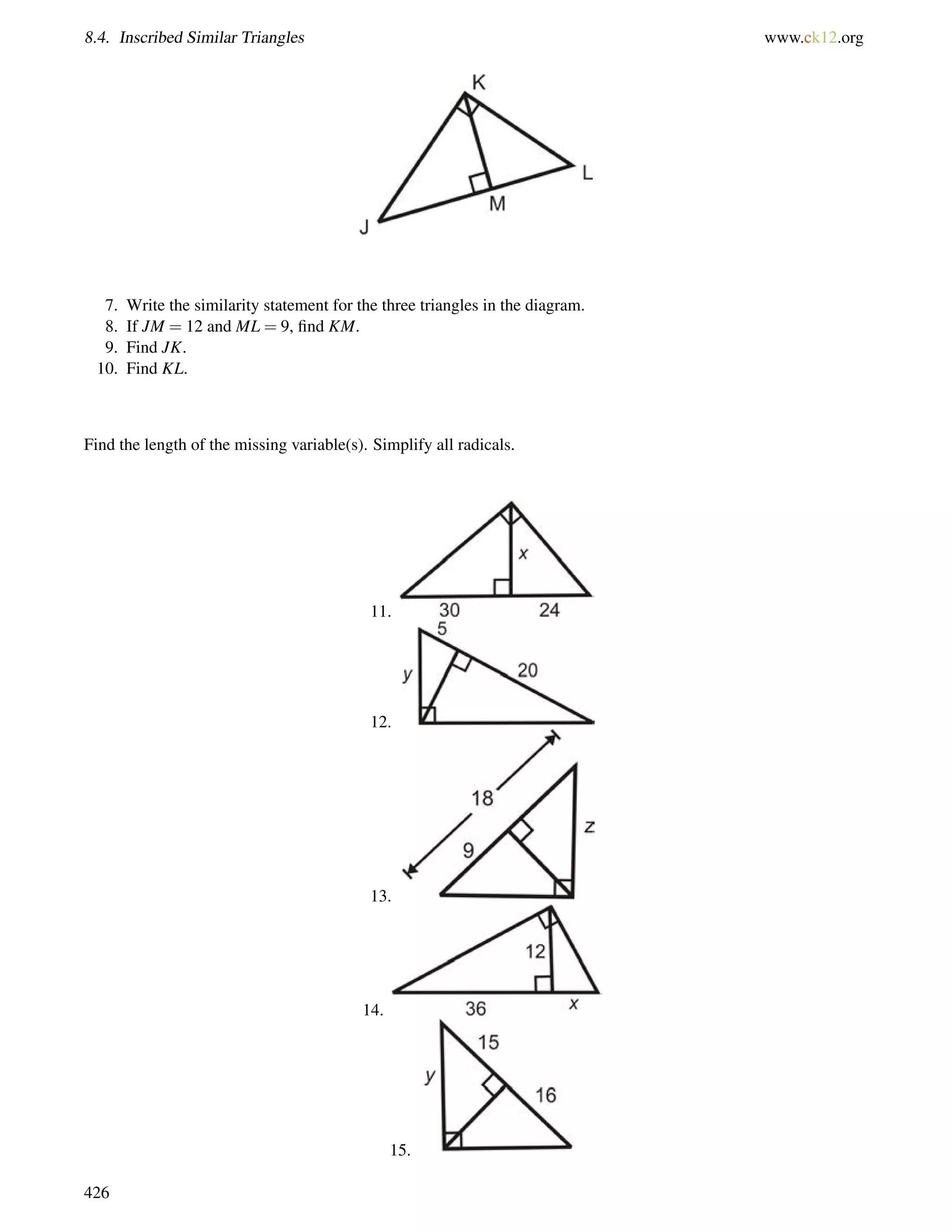
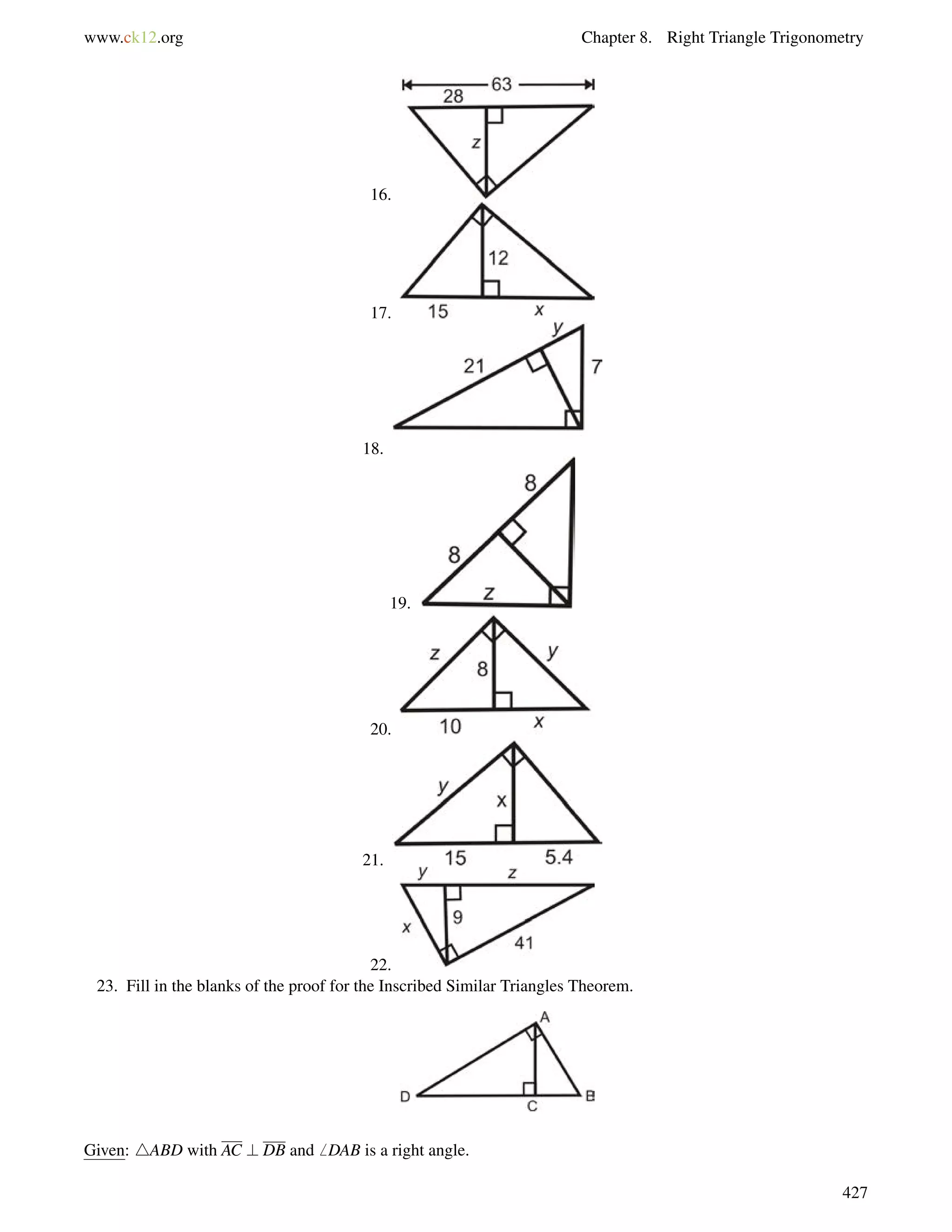





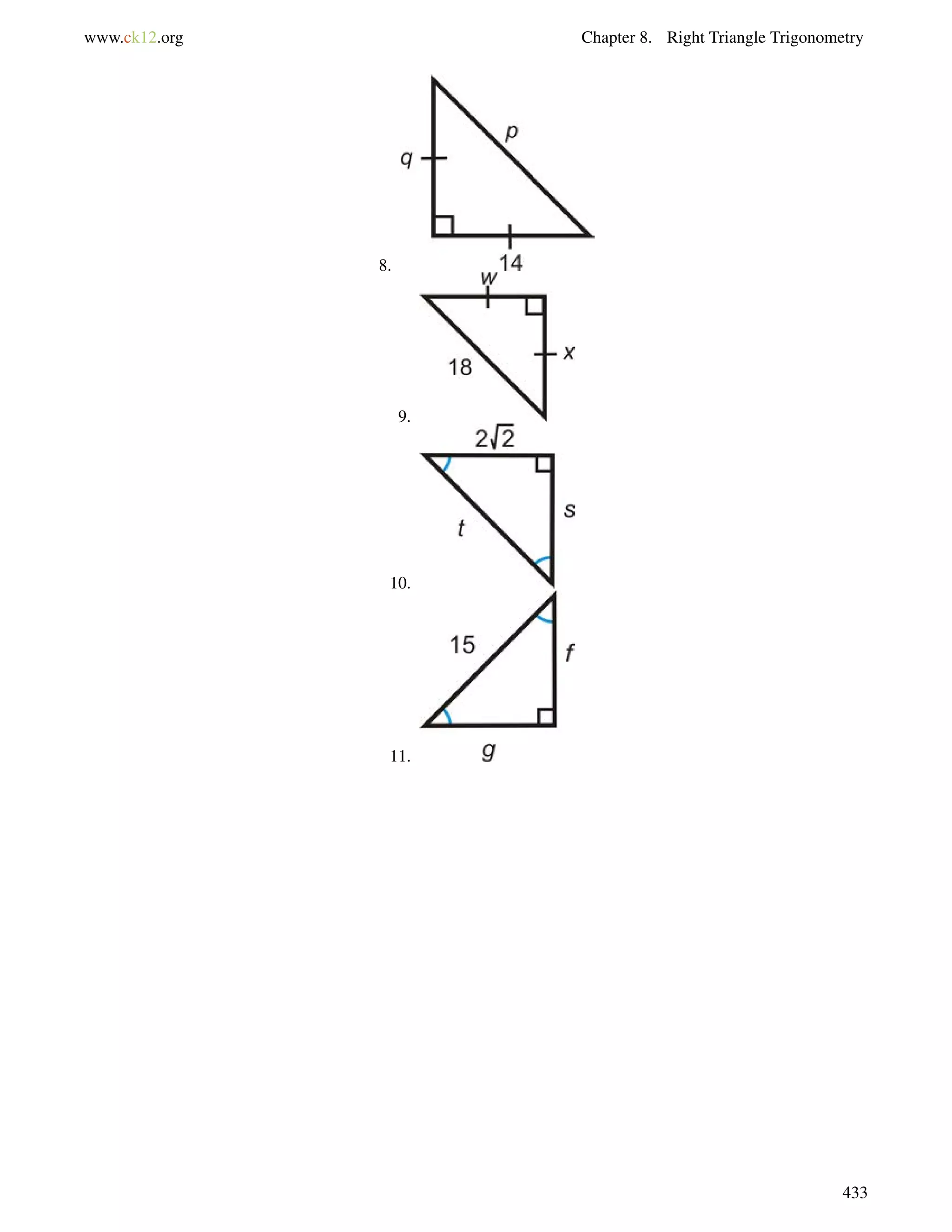




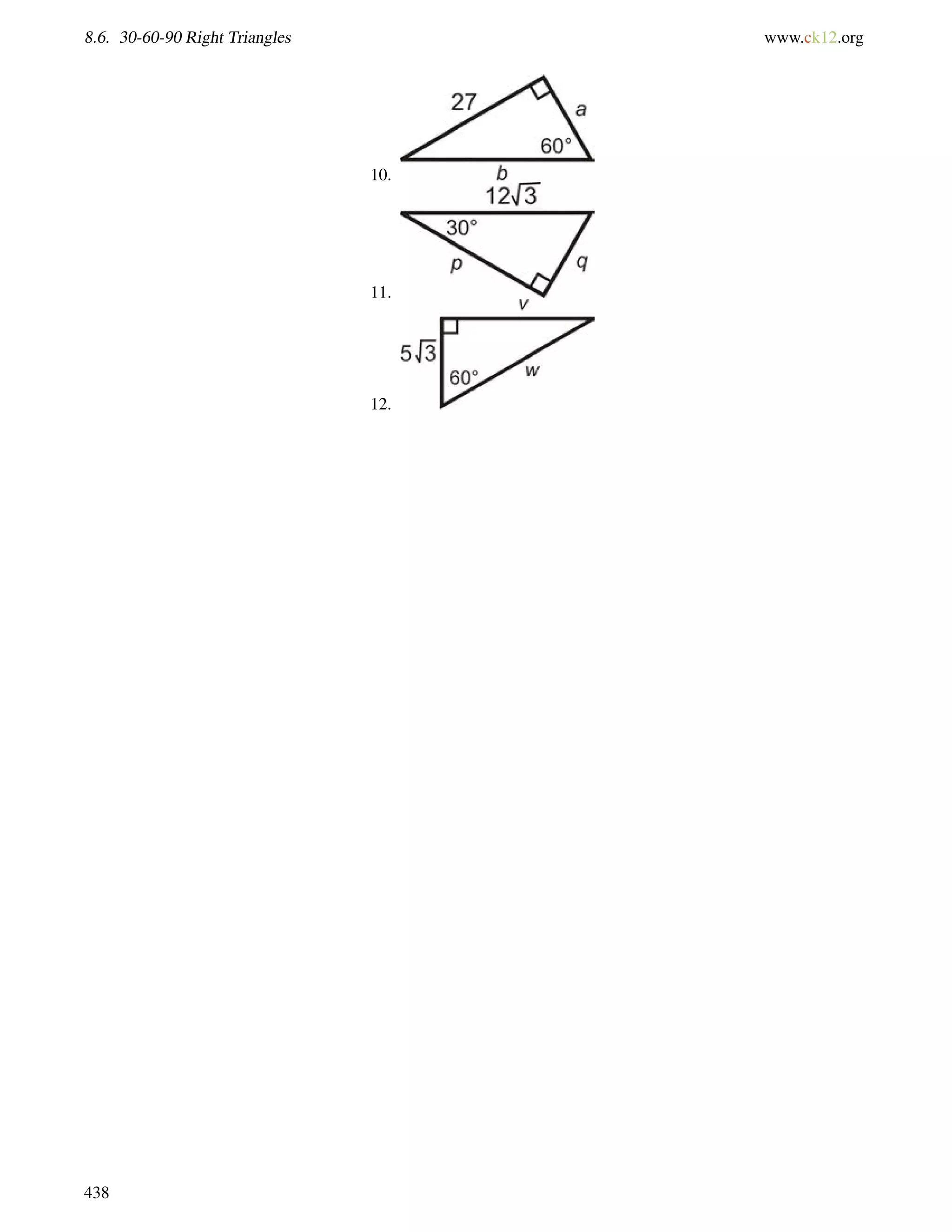

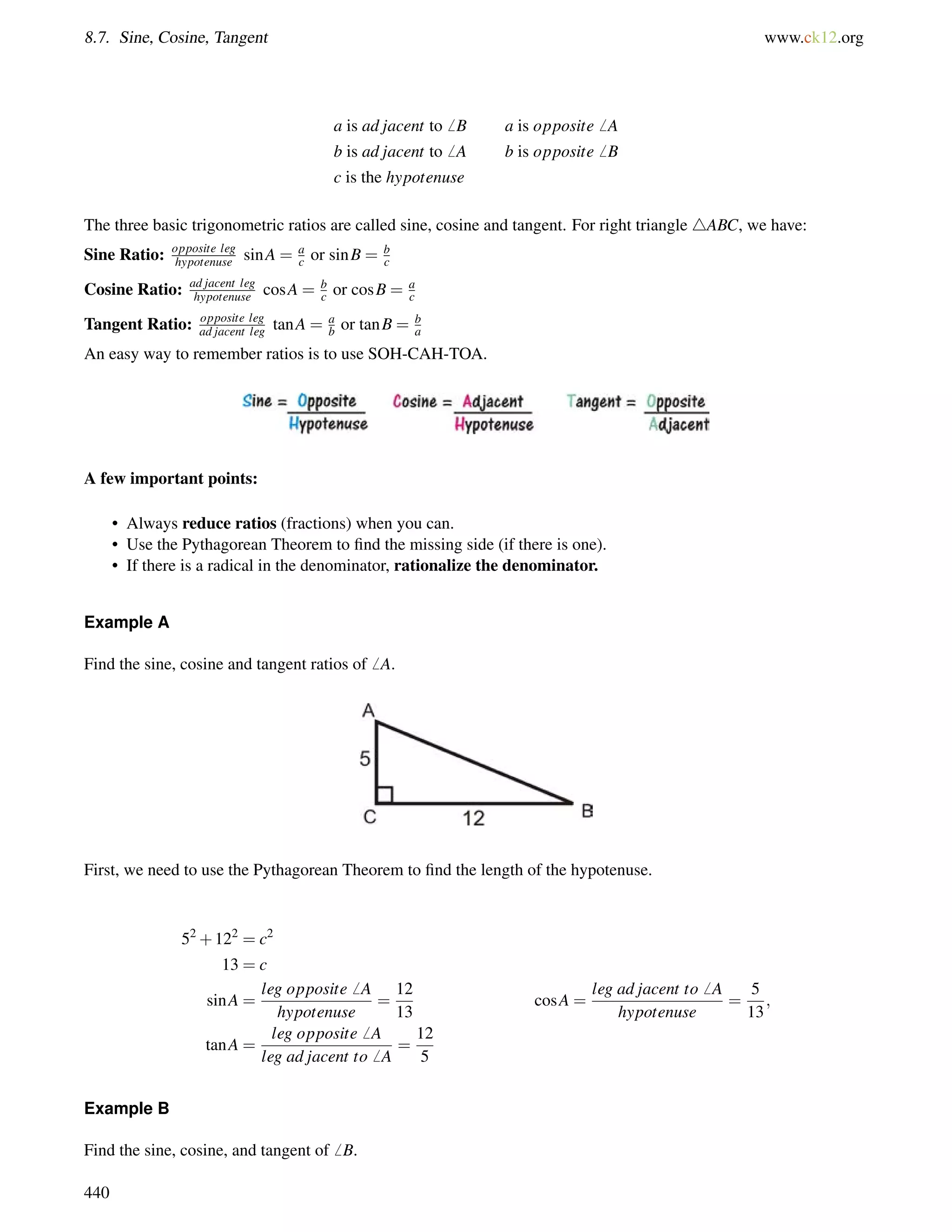


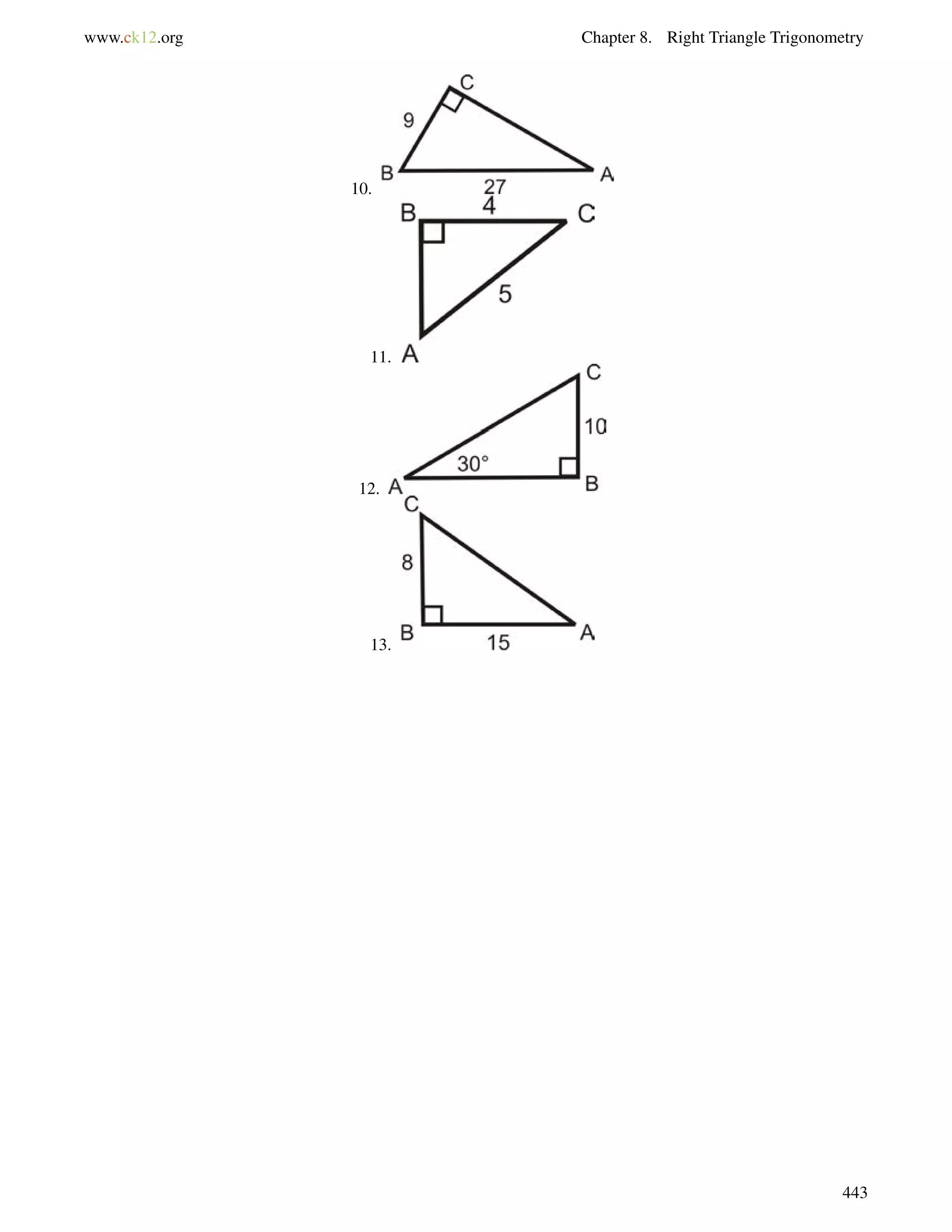
![8.8. Trigonometric Ratios with a Calculator www.ck12.org
8.8 Trigonometric Ratios with a Calculator
Here you’ll learn how to solve for missing sides in right triangles that are not one of the special right triangles.
What if you were given a 20-70-90 triangle? How could you find the sine, cosine, and tangent of the 20 and 70
angles? After completing this Concept, you’ll be able to use a calculator to find the trigonometric ratios for angles
that do not measure 45, 30, or 60.
Watch This
MEDIA
Click image to the left for more content.
CK-12 Foundation: The Trigonometric Ratios with a Calculator
MEDIA
Click image to the left for more content.
James Sousa:DeterminingTrigonometric Function Values on the Calculator
Guidance
There is a fixed sine, cosine, and tangent value for every angle, from 0 to 90. Your scientific (or graphing)
calculator knows all the trigonometric values for any angle. Your calculator, should have [SIN], [COS], and [TAN]
buttons. You can use your calculator and the trigonometric ratios is to find the missing sides of a right triangle by
setting up a trig equation.
Example A
Find the trigonometric value, using your calculator. Round to 4 decimal places.
a) sin78
b) cos60
c) tan15
Depending on your calculator, you enter the degree and then press the trig button or the other way around. Also,
make sure the mode of your calculator is in DEGREES.
444](https://image.slidesharecdn.com/ck-12-basic-geometry-conceptsbv10tfrs1reduced-141002074324-phpapp01/75/Ck-12-basic-geometry-concepts-450-2048.jpg)









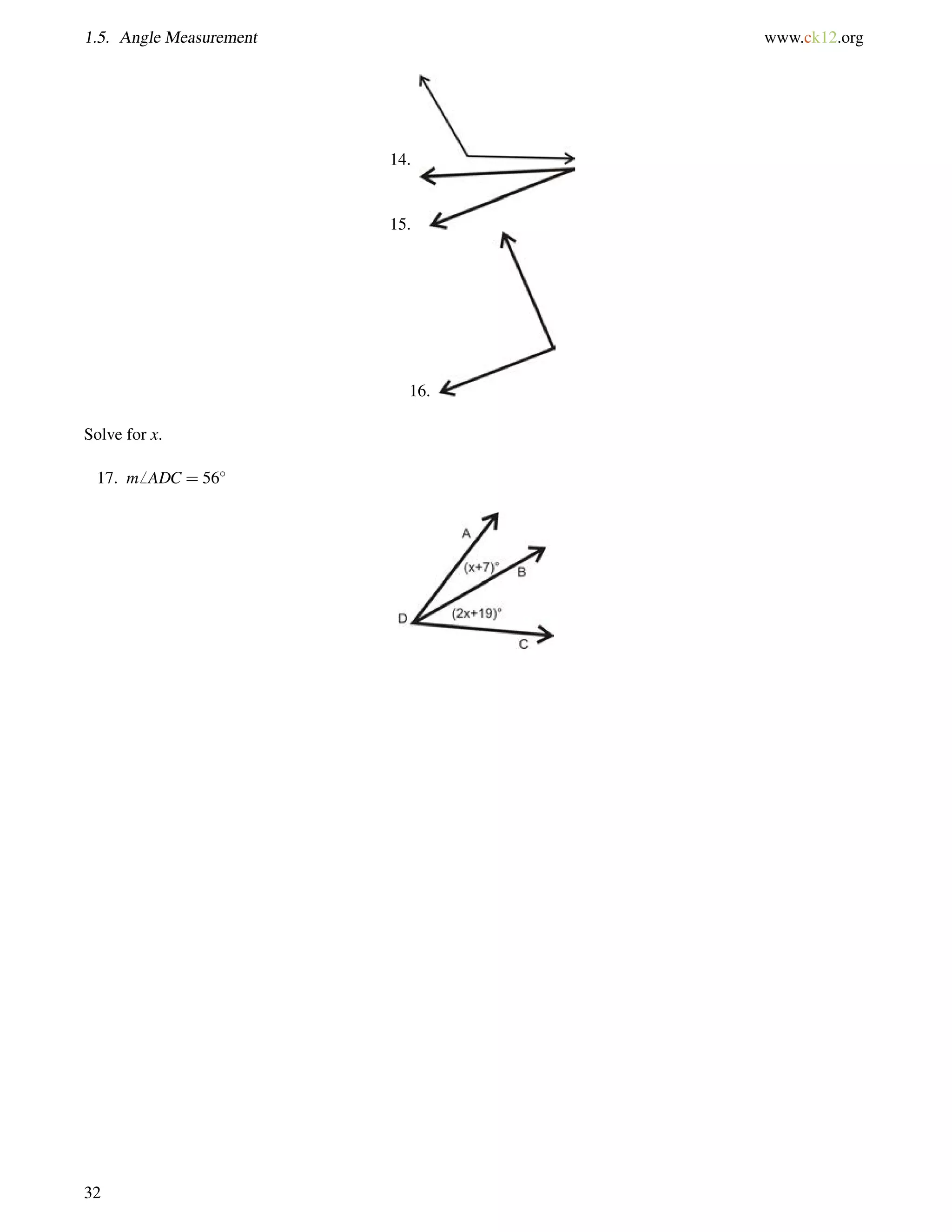
![8.10. Inverse Trigonometric Ratios www.ck12.org
sin1 bc
= m6 B and sin1 ac
= m6 A.
bc
ac
Inverse Cosine: Labeled cos1.
cos1 = m6 B and cos1
= m6 A.
In most problems, to find the measure of the angles you will need to use your calculator. On most scientific and
graphing calculators, the buttons look like [SIN1]; [COS1], and [TAN1]. You might also have to hit a shift or 2nd
button to access these functions.
Now that you know both the trig ratios and the inverse trig ratios you can solve a right triangle. To solve a right
triangle, you need to find all sides and angles in it. You will usually use sine, cosine, or tangent; inverse sine, inverse
cosine, or inverse tangent; or the Pythagorean Theorem.
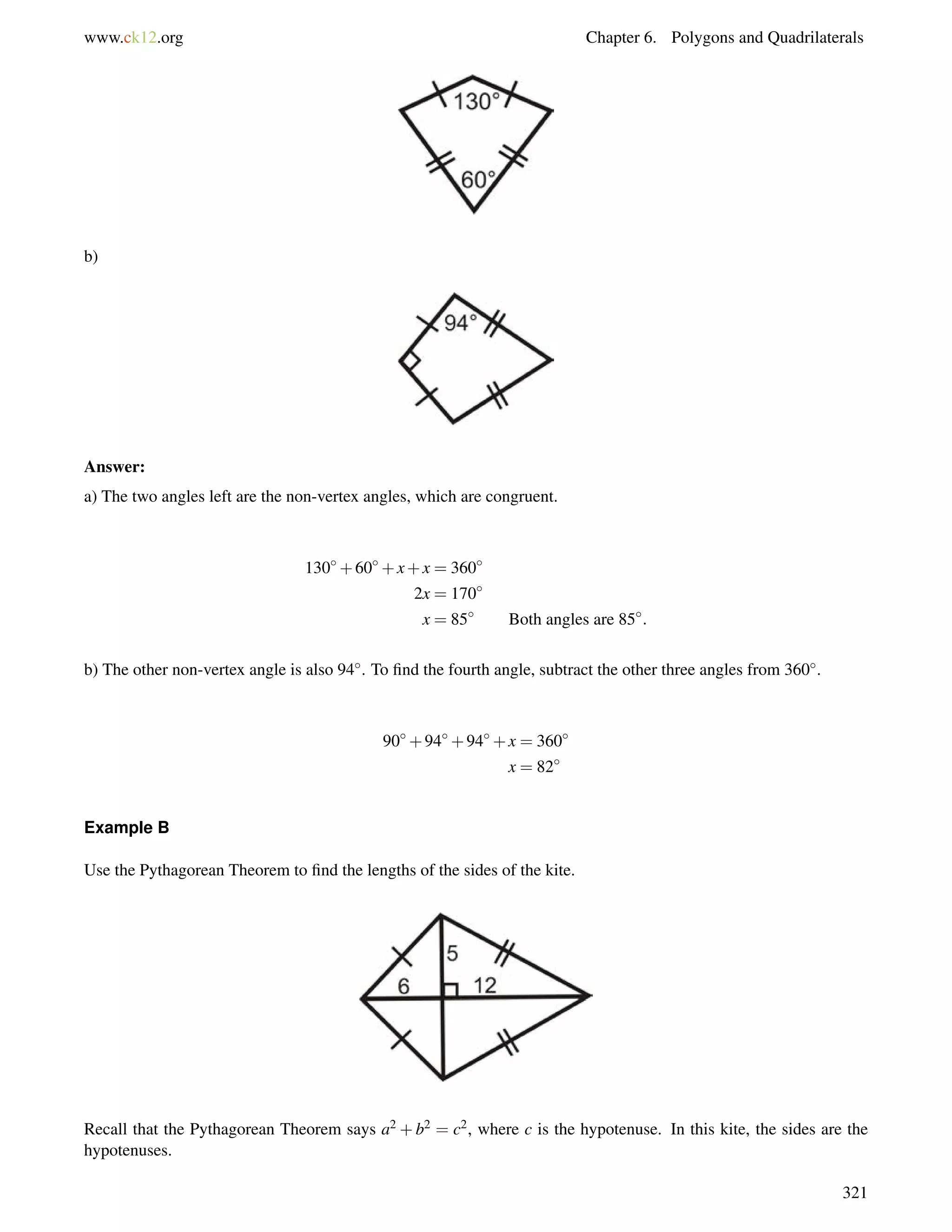
Example A
Use the sides of the triangle and your calculator to find the value of6 A. Round your answer to the nearest tenth of a
degree.
In reference to6 A, we are given the opposite leg and the adjacent leg. This means we should use the tangent ratio.
tanA = 20
25 = 45
. So, tan1 45
= m6 A. Now, use your calculator.
45
If you are using a TI-83 or 84, the keystrokes would be: [2nd][TAN]
[ENTER] and the screen looks like:
m6 A 38:7
Example B
6 A is an acute angle in a right triangle. Find m6 A to the nearest tenth of a degree.
a) sinA = 0:68
b) cosA = 0:85
c) tanA = 0:34
Answers:
a) m6 A = sin1 0:68 42:8
b) m6 A = cos1 0:85 31:8
c) m6 A = tan1 0:34 18:8
454](https://image.slidesharecdn.com/ck-12-basic-geometry-conceptsbv10tfrs1reduced-141002074324-phpapp01/75/Ck-12-basic-geometry-concepts-460-2048.jpg)