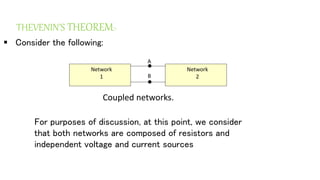
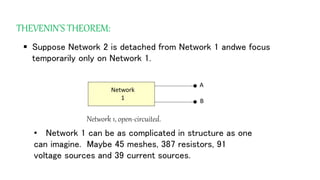
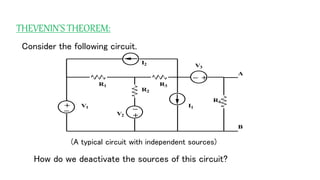
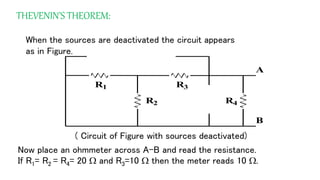
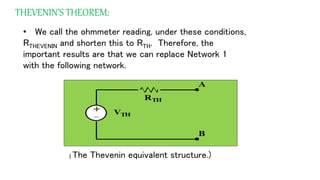
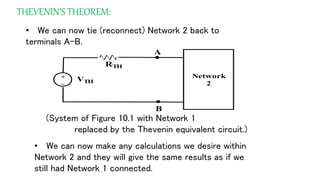
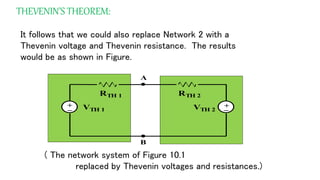
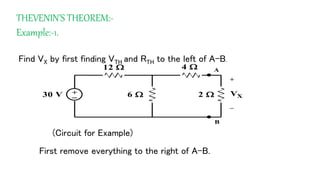
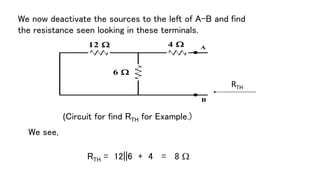
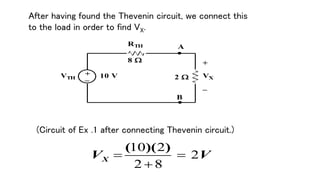
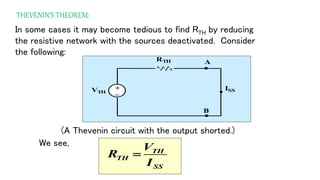
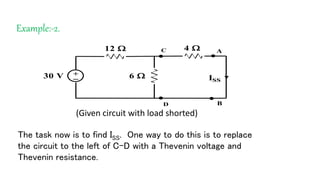
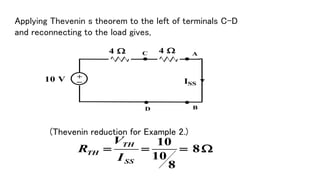
The document discusses Thevenin's theorem, which states that any linear electrical network can be reduced to an equivalent circuit consisting of a voltage source VTH in series with a resistor RTH. It provides examples of finding the Thevenin equivalent circuit for given networks by calculating VTH with open circuits and RTH with deactivated sources. This allows the complex network to be replaced by a simplified model for analysis or connection to other circuits.

1. Arham Veerayatan Institute
Of
Engineering, Technology
&
Research.(Mandvi)
Made by:-
Matang.Prabhat.D
(150920109001)
Guided by:-
Prof.kashyappuri Goswami.
THEVENIN
Circuit &
Network

2. THEVENIN’S THEOREM:-
 Consider the following:
Network
1
Network
2
•
•
A
B
Coupled networks.
For purposes of discussion, at this point, we consider
that both networks are composed of resistors and
independent voltage and current sources

3. THEVENIN’S THEOREM:
 Suppose Network 2 is detached from Network 1 andwe focus
temporarily only on Network 1.
Network
1
•
•
A
B
Network 1, open-circuited.
• Network 1 can be as complicated in structure as one
can imagine. Maybe 45 meshes, 387 resistors, 91
voltage sources and 39 current sources.

4. Network
1
•
•
A
B
THEVENIN’S THEOREM:
Now place a voltmeter across terminals A-B and
read the voltage. We call this the open-circuit voltage.
No matter how complicated Network 1 is, we read one
voltage. It is either positive at A, (with respect to B)
or negative at A.
We call this voltage Vos and we also call it
VTHEVENIN = VTH

5. THEVENIN’S THEOREM:
• We now deactivate all sources of Network 1.
• To deactivate a voltage source, we remove
the source and replace it with a short circuit.
• To deactivate a current source, we remove
the source.

6. THEVENIN’S THEOREM:
Consider the following circuit.
+_
+
+
_ _
A
B
V1
I2
V2
I1
V3
R1
R2
R3
R4
(A typical circuit with independent sources)
How do we deactivate the sources of this circuit?

7. THEVENIN’S THEOREM:
When the sources are deactivated the circuit appears
as in Figure.
R1
R2
R3
R4
A
B
( Circuit of Figure with sources deactivated)
Now place an ohmmeter across A-B and read the resistance.
If R1= R2 = R4= 20  and R3=10  then the meter reads 10 .

8. THEVENIN’S THEOREM:
• We call the ohmmeter reading, under these conditions,
RTHEVENIN and shorten this to RTH. Therefore, the
important results are that we can replace Network 1
with the following network.
VTH
RTH
A
B
+_


( The Thevenin equivalent structure.)

9. THEVENIN’S THEOREM:
• We can now tie (reconnect) Network 2 back to
terminals A-B.
A
B
Network
2
VTH
RTH
+
_


(System of Figure 10.1 with Network 1
replaced by the Thevenin equivalent circuit.)
• We can now make any calculations we desire within
Network 2 and they will give the same results as if we
still had Network 1 connected.

10. THEVENIN’S THEOREM:
It follows that we could also replace Network 2 with a
Thevenin voltage and Thevenin resistance. The results
would be as shown in Figure.
A
B
+ +_ _
RTH 1 RTH 2
VTH 1 VTH 2


( The network system of Figure 10.1
replaced by Thevenin voltages and resistances.)

11. THEVENIN’S THEOREM:-
Example:-1.
Find VX by first finding VTH and RTH to the left of A-B.
12  4 
6  2  VX30 V +_
+
_
A
B


(Circuit for Example)
First remove everything to the right of A-B.

12. 12  4 
6 30 V +_
A
B


(Circuit for finding VTH for Example )
(30)(6)
10
6 12
ABV V 

Notice that there is no current flowing in the 4  resistor
(A-B) is open. Thus there can be no voltage across the
resistor.

13. We now deactivate the sources to the left of A-B and find
the resistance seen looking in these terminals.
12  4 
6 
A
B


RTH
(Circuit for find RTH for Example.)
We see,
RTH = 12||6 + 4 = 8 

14. After having found the Thevenin circuit, we connect this
to the load in order to find VX.
8 
10 VVTH
RTH
2  VX
+
_
+
_
A
B


(Circuit of Ex .1 after connecting Thevenin circuit.)
10 2
2
2 8
 

( )( )
XV V

15. THEVENIN’S THEOREM:
In some cases it may become tedious to find RTH by reducing
the resistive network with the sources deactivated. Consider
the following:
VTH
RTH
+
_
A
B


ISS
(A Thevenin circuit with the output shorted.)
We see,
TH
TH
SS
V
R
I


16. Example:-2.
12  4 
6 30 V +_
A
B


ISS


C
D
(Given circuit with load shorted)
The task now is to find ISS. One way to do this is to replace
the circuit to the left of C-D with a Thevenin voltage and
Thevenin resistance.

17. Applying Thevenin s theorem to the left of terminals C-D
and reconnecting to the load gives,
4  4 
10 V +_
A
B


ISS


C
D
(Thevenin reduction for Example 2.)
10
8
10
8
TH
TH
SS
V
R
I
   