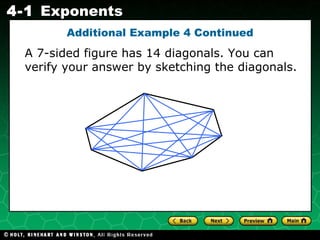
The document provides examples and explanations of exponents and exponential notation. It includes examples of writing expressions in exponential form, simplifying expressions with exponents, using the order of operations with exponents, and an application involving finding the number of diagonals in a polygon using an exponential expression.

1. Warm Up California Standards Lesson Presentation Preview

2. Warm Up Find the product. 625 1. 5 • 5 • 5 • 5 2. 3 • 3 • 3 3. (–7) • (–7) • (–7) 4. 9 • 9 27 – 343 81

3. AF2.1 Interpret positive whole-number powers as repeated multiplication and negative whole-number powers as repeated division or multiplication by the multiplicative inverse. Simplify and evaluate expressions that include exponents. Also covered: AF1.2 California Standards

4. Vocabulary exponential form exponent base power

5. If a number is in exponential form , the exponent represents how many times the base is to be used as a factor. A number produced by raising a base to an exponent is called a power . 27 and 3 3 are equivalent. 7 Exponent Base 2

6. Identify how many times 4 is a factor. Write in exponential form. Additional Example 1: Writing Exponents A. 4 • 4 • 4 • 4 Identify how many times –6 is a factor. (–6) • (–6) • (–6) = (–6) 3 B. (–6) • (–6) • (–6) 4 • 4 • 4 • 4 = 4 4 Read (–6) 3 as “–6 to the 3rd power" or "–6 cubed”. Reading Math

7. Identify how many times 5 and d are each used as a factor. Additional Example 1: Writing Exponents C. 5 • 5 • d • d • d • d Write in exponential form. 5 • 5 • d • d • d • d = 5 2 d 4

8. Identify how many times x is a factor. Write in exponential form. Check It Out! Example 1 A. x • x • x • x • x Identify how many times d is a factor. B. d • d • d x • x • x • x • x = x 5 d • d • d = d 3

9. Identify how many times 7 and b are each used as a factor. 7 • 7 • b • b = 7 2 b 2 Check It Out! Example 1 C. 7 • 7 • b • b Write in exponential form.

10. = 243 3 5 = 3 • 3 • 3 • 3 • 3 Find the product. Find the product. B. Simplify. Additional Example 2: Simplifying Powers A. 3 5 = 1 27

11. = 256 – 2 8 = –(2 • 2 • 2 • 2 • 2 • 2 • 2 • 2) = –256 Simplify. Additional Example 2: Simplifying Powers Find the product. Find the product. Then make the answer negative. D. – 2 8 = (–4) • (–4) • (–4) • (–4) (–4) 4 C. (–4) 4

12. The expression (–4) 4 is not the same as the expression –4 4 . Think of –4 4 as –1 ● 4 4 . By the order of operations, you must evaluate the exponent before multiplying by –1 . Caution!

13. = 2401 7 4 = 7 • 7 • 7 • 7 Find the product. Simplify. Check It Out! Example 2 Find the product. A. 7 4 B. = 1 8

14. = 25 – 9 4 = –(9 • 9 • 9 • 9) = –6,561 Evaluate. Find the product. Find the product. Then make the answer negative. Check It Out! Example 2 D. – 9 4 = (–5) • ( – 5) (–5) 2 C. (–5) 2

15. Additional Example 3: Using the Order of Operations 4(7) + 16 Substitute 4 for x, 2 for y, and 3 for z. Simplify the powers. Subtract inside the parentheses. Multiply from left to right. 4(2 4 – 3 2 ) + 4 2 4(16 – 9) + 16 28 + 16 Add. 44 Evaluate x ( y x – z y ) + x for x = 4, y = 2, and z = 3. y x ( y x – z y ) + x y

16. Check It Out! Example 3 60 – 7(7) Substitute 5 for x, 2 for y, and 60 for z. Simplify the powers. Subtract inside the parentheses. Multiply from left to right. 60 – 7(2 5 – 5 2 ) 60 – 7(32 – 25) 60 – 49 Subtract. 11 Evaluate z – 7(2 x – x y ) for x = 5, y = 2, and z = 60. z – 7(2 x – x y )

17. Additional Example 4: Geometry Application Simplify inside the parentheses. Multiply. Substitute the number of sides for n. Subtract inside the parentheses. 14 diagonals Use the expression ( n 2 – 3 n ) to find the number of diagonals in a 7-sided figure. (7 2 – 3 • 7) 1 2 (49 – 21) 1 2 ( n 2 – 3 n ) 1 2 (28) 1 2 1 2

18. A 7-sided figure has 14 diagonals. You can verify your answer by sketching the diagonals. Additional Example 4 Continued

19. Check It Out! Example 4 Simplify inside the parentheses. Multiply Substitute the number of sides for n. Subtract inside the parentheses. 2 diagonals Use the expression ( n 2 – 3 n ) to find the number of diagonals in a 4-sided figure. (4 2 – 3 • 4) 1 2 (16 – 12) 1 2 ( n 2 – 3 n ) 1 2 (4) 1 2 1 2

20. A 4-sided figure has 2 diagonals. You can verify your answer by sketching the diagonals. Check It Out! Example 4 Continued

21. Lesson Quiz Write in exponential form. 1. n • n • n • n 2. (–8) • (–8) • (–8) • ( h ) 256 – 213 (–8) 3 h 3. (–4) 4 5. Evaluate xz – y x for x = 5, y = 3, and z = 6. 6. A population of bacteria doubles in size every minute. The number of bacteria after 5 minutes is 15  2 5 . How many are there after 5 minutes? 480 Simplify. 4. n 4