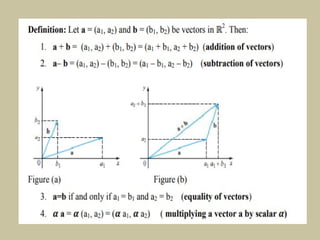
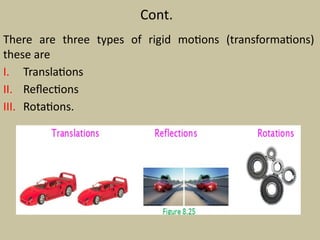
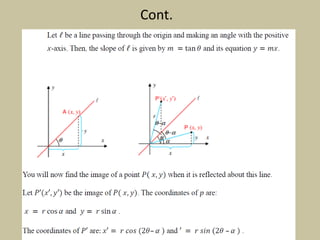
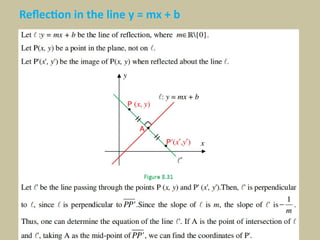
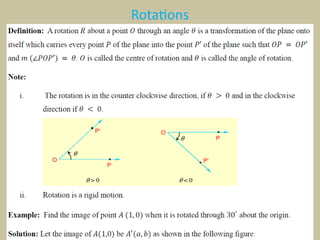
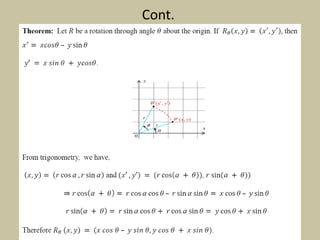
Chapter five of the compiled mathematics module focuses on vectors, defining them as quantities with both magnitude and direction, contrasting them with scalars. It discusses vector operations such as addition and scalar multiplication, and explains three types of rigid transformations: translations, reflections, and rotations. The chapter includes mathematical definitions and examples related to these concepts.