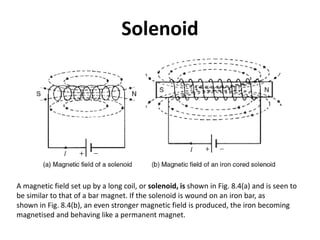
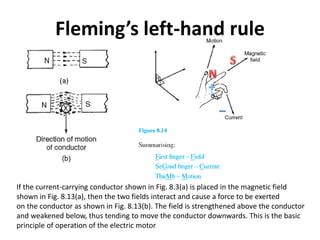
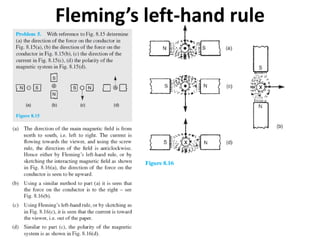
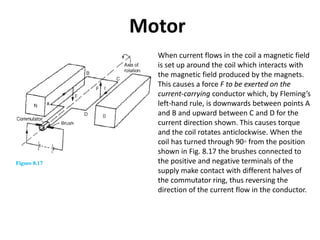
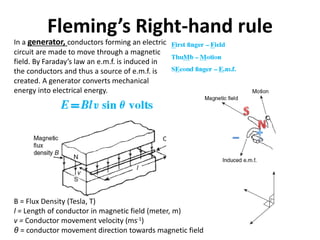
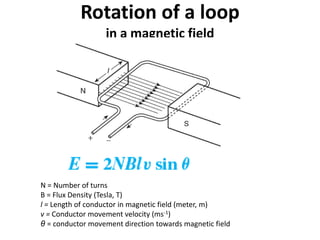
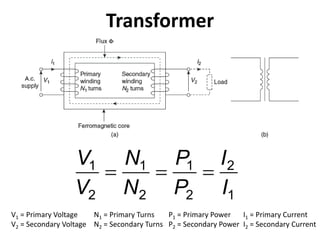
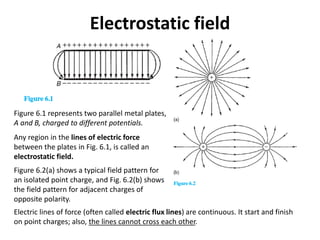
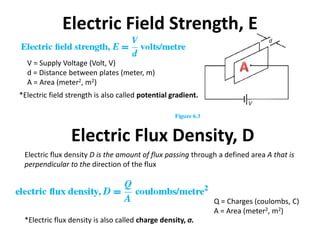
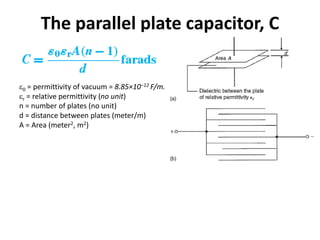
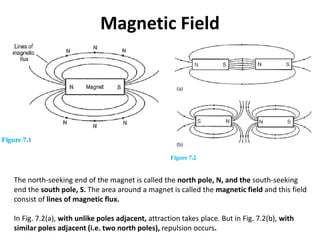
The document discusses electric and magnetic fields, including: - An electric field is established between two parallel metal plates charged to different potentials. - Magnetic field lines originate and terminate on magnetic poles. Unlike poles attract while like poles repel. - Electromagnetic induction occurs when a changing magnetic field induces an electric current in a conductor. The direction of the induced current opposes the change according to Lenz's law.

2. Electric Field

3. Figure 6.1 represents two parallel metal plates,
A and B, charged to different potentials.
Any region in the lines of electric force
between the plates in Fig. 6.1, is called an
electrostatic field.
Figure 6.2(a) shows a typical field pattern for
an isolated point charge, and Fig. 6.2(b) shows
the field pattern for adjacent charges of
opposite polarity.
Electrostatic field
Electric lines of force (often called electric flux lines) are continuous. It start and finish
on point charges; also, the lines cannot cross each other.

4. V = Supply Voltage (Volt, V)
d = Distance between plates (meter, m)
A = Area (meter2, m2)
*Electric field strength is also called potential gradient.
Electric Field Strength, E
Electric flux density D is the amount of flux passing through a defined area A that is
perpendicular to the direction of the flux
*Electric flux density is also called charge density, σ.
Q = Charges (coulombs, C)
A = Area (meter2, m2)
Electric Flux Density, D

7. Capacitance, C
Q = Charges (coulombs, C)
V = Volt Applied (Volt, V)
How much charge corresponds to a given p.d. between the plates is the capacitance:
Permittivity, 
0 = permittivity of vacuum = 8.85×10−12 F/m.
r = relative permittivity (no unit)
D = Electric Flux Density (C/m2)
E = Electric Field Strenth (v/m)
CONST 32 =
Typical values of εr include air, 1.00; polythene,
2.3; mica, 3–7; glass, 5–10; water, 80; ceramics, 6–1000.
I = Current (Ampere, A)
t = time (seconds, s)
Electrostatic Field established in particular materials

10. The parallel plate capacitor, C
0 = permittivity of vacuum = 8.85×10−12 F/m.
r = relative permittivity (no unit)
n = number of plates (no unit)
d = distance between plates (meter/m)
A = Area (meter2, m2)

11. Dielectric Strength, Em
Vm = Supply Voltage (Volt, V)
d = Distance between plates (meter, m)

14. Energy stored in capacitors, W
V = Voltage Applied(Volt, V)
C = Capacitance (Farad, F)

16. Magnetic Field

17. Magnetic Field
The north-seeking end of the magnet is called the north pole, N, and the south-seeking
end the south pole, S. The area around a magnet is called the magnetic field and this field
consist of lines of magnetic flux.
In Fig. 7.2(a), with unlike poles adjacent, attraction takes place. But in Fig. 7.2(b), with
similar poles adjacent (i.e. two north poles), repulsion occurs.

18. Magnetic Flux
Magnetic flux is the amount of magnetic field (or the number of lines of force)
produced by a magnetic source. The symbol for magnetic flux is φ (Greek letter ‘phi’).
The unit of magnetic flux is the weber, Wb. Magnetic flux density is the amount of
flux passing through a defined area that is perpendicular to the direction of the flux
Flux Density, B
φ = Magnetic Flux (weber, Wb)
A = Area (meter2, m2)
The symbol for magnetic flux density is B. The unit of magnetic flux density is the
tesla, T, where 1 T = 1Wb/m2.

20. Magnetomotive force, mmf
Magnetomotive force (m.m.f.) is the cause of the existence of a magnetic flux in a
magnetic circuit
Magnetic Field Strength
N = Number of turns (No Unit)
I = Current (Ampere, A)
l = Magnetic Path (Meter, m)
N = Number of turns (No Unit)
I = Current (Ampere, A)

21. Flux, Flux Density & Mmf

22. Electromagnetism

23. Magnetic field due to an
electric current
If a current is now passed through the wire,
then the iron filings will forma definite
circular field pattern with the wire at the
centre. If the current direction is reversed,
the direction of the lines of flux is also
reversed.

24. Screw Rule
The direction of the magnetic lines of flux is best remembered by the screw rule which
states that:
If a normal right-hand thread screw is screwed along the conductor in the direction of the
current, the direction of rotation of the screw is in the direction of the magnetic field.
*screw rule = right hand grip rule

25. Solenoid
A magnetic field set up by a long coil, or solenoid, is shown in Fig. 8.4(a) and is seen to
be similar to that of a bar magnet. If the solenoid is wound on an iron bar, as
shown in Fig. 8.4(b), an even stronger magnetic field is produced, the iron becoming
magnetised and behaving like a permanent magnet.

26. Fleming’s left-hand rule
If the current-carrying conductor shown in Fig. 8.3(a) is placed in the magnetic field
shown in Fig. 8.13(a), then the two fields interact and cause a force to be exerted
on the conductor as shown in Fig. 8.13(b). The field is strengthened above the conductor
and weakened below, thus tending to move the conductor downwards. This is the basic
principle of operation of the electric motor

27. Fleming’s left-hand rule

28. Motor
When current flows in the coil a magnetic field
is set up around the coil which interacts with
the magnetic field produced by the magnets.
This causes a force F to be exerted on the
current-carrying conductor which, by Fleming’s
left-hand rule, is downwards between points A
and B and upward between C and D for the
current direction shown. This causes torque
and the coil rotates anticlockwise. When the
coil has turned through 90◦ from the position
shown in Fig. 8.17 the brushes connected to
the positive and negative terminals of the
supply make contact with different halves of
the commutator ring, thus reversing the
direction of the current flow in the conductor.

29. Electromagnetic Induction
(a) When the magnet is moved at constant speed
towards the coil (Fig. 9.1(a)), a deflection is noted
on the galvanometer showing that a current has
been produced in the coil.
(b) When the magnet is moved at the same speed
as in (a) but away from the coil the same deflection
is noted but is in the opposite direction (see
Fig. 9.1(b)).
(c) When the magnet is held stationary, even
within the coil, no deflection is recorded.
(d) When the coil is moved at the same speed as
in (a) and the magnet held stationary the same
galvanometer deflection is noted.
(e) When the relative speed is, say, doubled, the
galvanometer deflection is doubled.
(f ) When a stronger magnet is used, a greater
galvanometer deflection is noted.
(g) When the number of turns of wire of the coil
is increased, a greater galvanometer deflection is
noted.
As the magnet is moved towards the
coil, the magnetic flux of the magnet
moves across, or cuts, the coil. It is the
relative movement of the magnetic flux
and the coil that causes an e.m.f. and
thus current, to be induced in the coil.
This effect is known as electromagnetic
induction.

30. Faraday’s laws
• Faraday’s law state that the voltage induced
across a coil of wire equals the number of
turns in the coil, multiply the rate of change of
the magnetic flux.
Lenz’s laws
• Lenz’s law state that when the current
through a coil changes, the polarity of the
induced voltage is such it always oppose the
change in current.

31. Fleming’s Right-hand rule
B = Flux Density (Tesla, T)
l = Length of conductor in magnetic field (meter, m)
v = Conductor movement velocity (ms-1)
θ = conductor movement direction towards magnetic field
In a generator, conductors forming an electric
circuit are made to move through a magnetic
field. By Faraday’s law an e.m.f. is induced in
the conductors and thus a source of e.m.f. is
created. A generator converts mechanical
energy into electrical energy.

32. Induced e.m.f.

33. Rotation of a loop
in a magnetic field
N = Number of turns
B = Flux Density (Tesla, T)
l = Length of conductor in magnetic field (meter, m)
v = Conductor movement velocity (ms-1)
θ = conductor movement direction towards magnetic field

34. Rotation of a loop
in a magnetic field

35. Energy stored in inductor, W
I = Current flows (Ampere, I)
L = Inductance (Henry, H)

36. Ideal Transformer

37. Transformer
1
2
2
1
2
1
2
1
I
I
P
P
N
N
V
V

V1 = Primary Voltage
V2 = Secondary Voltage
N1 = Primary Turns
N2 = Secondary Turns
P1 = Primary Power
P2 = Secondary Power
I1 = Primary Current
I2 = Secondary Current

38. Transformer 1
2
2
1
2
1
2
1
I
I
P
P
N
N
V
V


39. Transformer