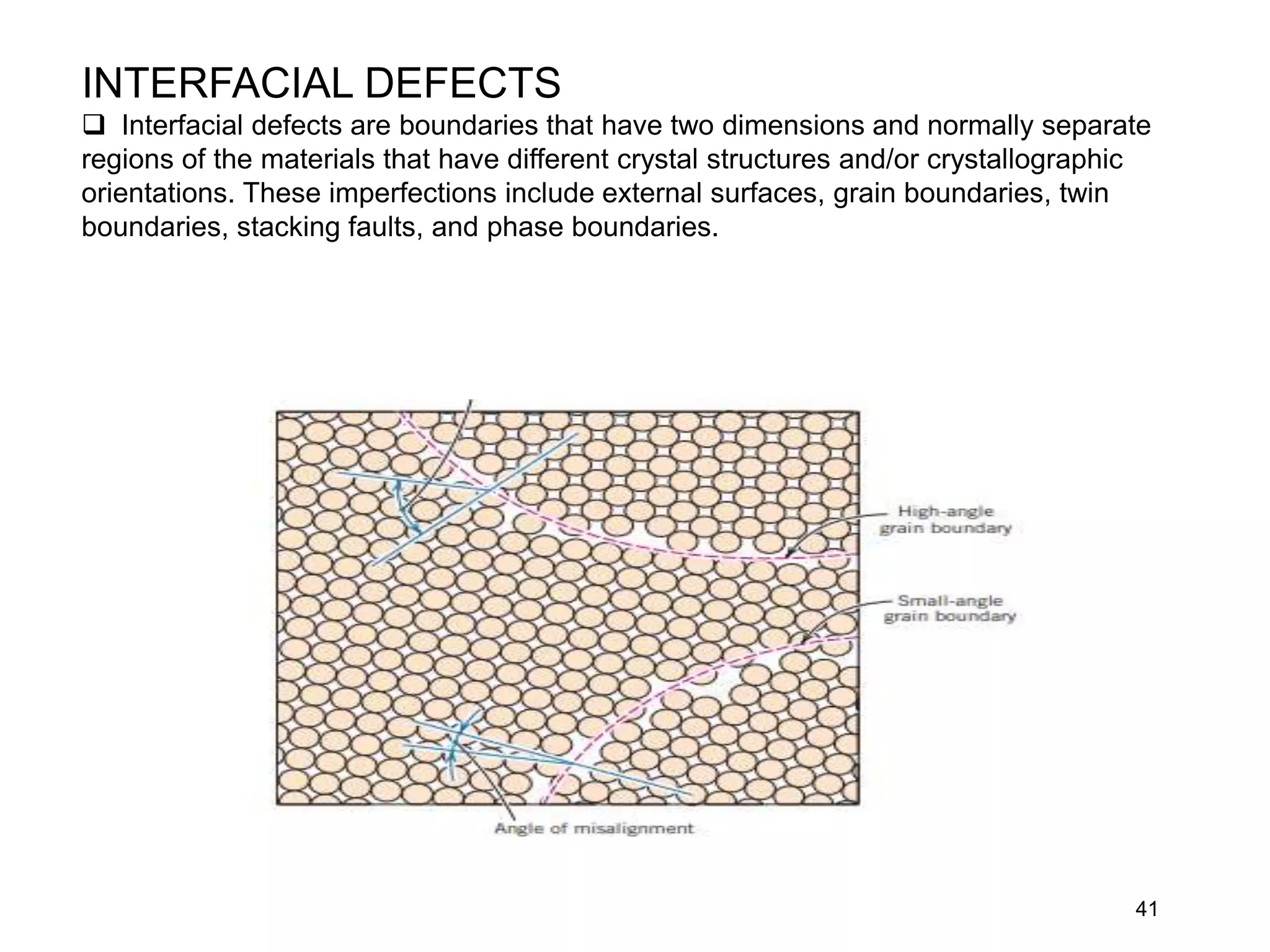
1. There are three main types of crystal imperfections - point defects, line defects, and interfacial defects. Point defects involve atoms being missing or in irregular positions in the lattice. Line defects are groups of atoms in irregular positions known as dislocations. Interfacial defects are boundaries separating regions with different crystal structures. 2. Solid solutions form when solute atoms are added to a solvent metal and the crystal structure is maintained. Factors like atomic radius, electronegativity, and crystal structure determine if a substitutional or interstitial solid solution forms. 3. Dislocations are line defects that allow plastic deformation to occur when they move in response to stress. Their motion produces slip between crystal planes

1. CHAPTER 3
CRYSTAL STRUCTURES
AND
IMPERFECTIONS
1

2. If the atoms or ions of a solid are arranged in a pattern
that repeats itself in three dimensions, they form a solid,
which is said to have a crystal structure and is referred to as
a crystalline material. Examples of crystalline materials
are metals, alloys, and some ceramic materials.

4. 3D_model_hydrogen_bonds_in
_water.

8. Most elemental metal (about 90 percent)
crystallize upon solidification into three densely
packed crystal structures.
The most common types of unit cells are
• body-centered cubic (BCC)
• face-centered cubic (FCC)
• hexagonal close-packed (HCP).
PRINCIPAL METALLIC CRYSTAL
STRUCTURES

11. The BCC crystal structure is not a close packed structure
.Many metals such as iron, chromium, tungsten,
molybdenum, and vanadium have the BCC crystal structure
at room temperature.

13. The two important characteristics of a crystal structure are the
coordination number (CN) and the atomic packing factor
(APF).
The coordination number for BCC crystal structure is 8; each
center atom has eight nearest neighbor atoms i.e at the corner
The APF is the fraction of the solid sphere volume in a unit cell by
total unit cell volume, assuming the atomic hard sphere model.
APF = Volume of atoms in a unit cell
Total unit cell volume
The atomic packing factor (APF) for the BCC unit cells, assuming
the atoms to be hard spheres is:
APF = Volume of atoms in BCC unit cell = Vs/Vc
Volume of BCC unit cell

15. metals have this crystal structure are copper, aluminum,
silver, and gold

20. The coordination number of the atoms in this structure is 12. There
are six nearest neighbors in the same close packed layer, three in the
layer above and three in the layer below. The packing factor is 0.74,
which is the same as the FCC unit cell. The HCP structure is very
common for elemental metals and some examples include beryllium,
cadmium, magnesium, titanium, zinc and zirconium

21. • Assignment
• Calculate the atomic packing
factor(APF) for hexagonal close packed
(HCP) crystal structure? Use diagram

22. Chapter 3
Imperfections

23. Why study Imperfections in Solids?
 The properties (mechanical, optical, electrical, etc.) of the
materials are profoundly influenced by the presence of
imperfections (defects)
• The influence is not always adverse(bad), often specific
characteristics are enhanced.
EXAMPLE 1: Mechanical property
• Materials are stronger when they have defects.
Pure iron & Fe-C alloy
Pure iron : soft and ductile
Fe-C alloy (steel) : strong and tough 23

24. Imperfections in Solids
• The properties of some materials are
profoundly influenced by the presence
of imperfections.
• It is important to have knowledge about
the types of imperfections that exist and
the roles they play in affecting the
behavior of materials.
24

25. 25
Atom Purity and Crystal Perfection
• If we assume a perfect crystal structure
containing pure elements, then anything
that deviated from this concept or
intruded in this uniform homogeneity
would be an imperfection.
1. There are no perfect crystals.
2. Many material properties are improved by
the presence of imperfections and
deliberately modified (alloying and
doping).

26. 26
• Vacancy atoms
• Interstitial atoms
• Substitutional atoms
Point defects
1-2 atoms
Types of Imperfections
• Dislocations Line defects
1-dimensional
• Grain Boundaries Area defects
2-dimensional

27. 1. POINT DEFECTS, which are places where an atom is
missing or irregularly placed in the lattice structure.
Point defects include lattice vacancies, self-interstitial
atoms, substitution impurity atoms, and interstitial
impurity atoms
2. LINEAR DEFECTS, which are groups of atoms in
irregular positions. Linear defects are commonly called
dislocations. Plastic deformation in a material occurs due
to the movement of dislocations (linear defects)
3. PLANAR DEFECTS, which are interfaces between
homogeneous regions of the material.
 Planar defects include grain boundaries, stacking faults
and external surfaces.

28. 28
• Vacancies:
-vacant atomic sites in a structure.
• Self-Interstitials:
-"extra" atoms positioned between atomic sites.
Point Defects in Metals
Vacancy
distortion
of planes
self-interstitial
distortion
of planes

29. Point Defects in Metals
• Substitutional atoms: For substitutional, solute or
impurity atoms replace or substitute for the host
atoms.
• Eg. Since Zn atoms are almost same size as Cu
atoms, Zn atoms can substitute for Cu atoms.
29

30. Cont…
• Non-equilibrium concentration of vacancies can be
generated by:
 quenching from a higher temperature
 bombardment with high energy particles
 plastic deformation.
 off-stoichiometry in ordered compounds. Etc.
• Stoichiometry may be defined as a state for ionic compounds
wherein there is the exact ratio of cations to anions
30

31. • In metals, a self interstitial introduces relatively large
distortions (strain) in the surrounding lattice since the
atom is substantially larger than the interstitial site.
Self Interstitials

32. 32
• Vacancies
-- vacancies exist in ceramics for both cations and anions
• Interstitials
-- interstitials exist for cations
-- interstitials are not normally observed for anions because anions
are large relative to the interstitial sites
Adapted from Fig. 5.2, Callister & Rethwisch 3e.
(Fig. 5.2 is from W.G. Moffatt, G.W. Pearsall, and
J. Wulff, The Structure and Properties of
Materials, Vol. 1, Structure, John Wiley and Sons,
Inc., p. 78.)
Point Defects in Ceramics
Cation Interstitial
Cation Vacancy
Anion Vacancy

33. 33
• Frenkel Defect
To maintain the charge neutrality, a cation vacancy-cation interstitial
pair occur together. The cation leaves its normal position and moves to the
interstitial site.
• Schottky Defect
To maintain the charge neutrality, remove 1 cation and 1 anion;
this creates 2 vacancies.
Adapted from Fig. 5.3, Callister & Rethwisch 3e.
(Fig. 5.3 is from W.G. Moffatt, G.W. Pearsall, and
J. Wulff, The Structure and Properties of
Materials, Vol. 1, Structure, John Wiley and Sons,
Inc., p. 78.)
Point Defects: Frenkel and Schottky
Schottky
Defect
Frenkel
Defect

34. 34
Boltzmann's constant
(1.38 x 10
-23
J/atom-K)
(8.62 x 10
-5
eV/atom-K)
 
Nv
N
= exp  Qv
kT






No. of defects
No. of potential
defect sites
Activation energy –
energy required for formation of vacancy
Temperature
Each lattice site
is a potential
vacancy site
• Equilibrium concentration varies with temperature.
Equilibrium Concentration:
Point Defects

35. Solid Solution
• The addition of impurity atoms to a metal results in
the formation of a solid solution.
• The solvent represents the element that is present
in the greatest amount (the host atoms).
• For example, in Precipitation Hardening of
Aluminum, aluminum is the solvent and copper is
the solute (present in minor concentration ).
• Solid solutions form when the solute atoms (Cu) are
added to the solvent (Al), assuming the crystal
structure is maintained and no new structures are
formed.
35

36. Solid Solution - continued
• A solid solution is a homogenous
composition throughout.
• The impurity atoms (Cu) are randomly and
uniformly dispersed within the solid.
• The impurity defects in the solid solution are
either substitutional or interstitial.
36

37. 37
What are the outcomes if impurity (B) is added to host (A)?
• Solid solution of B in A (random distribution of point defects)
• Solid solution of B in A plus particles of a new
phase (usually for a larger amount of B)
OR
Substitutional solid solution.
(e.g., Cu in Ni)
Interstitial solid solution.
(e.g., C in Fe)
Second phase particle
-- different composition
-- often different structure.
Imperfections in Metals

38. 38
Hume - Rothery Rules
The Hume-Rothery rules are basic conditions
for an element to dissolve in a metal, forming a
substitutional solid solution.
1. The atomic radius of the solute and solvent atoms
must differ by no more than 15% (r < 15%).
2. The solute and solvent should have similar
electronegativities.
3. Same crystal structure for “pure” metals.
4. Maximum solubility occurs when the solvent and
solute have the same valence. Metals with lower
valence will tend to dissolve metals with higher
valence.

39. • Carbon forms an interstitial solid solution when
added to iron; the maximum concentration of
carbon that can be added is roughly 2%.
• The atomic radius of the carbon atom is much
less than that of iron (0.071nm vs 0.124 nm).
• For interstitial solid solutions, the Hume-Rothery
rules are:
– 1. Solute atoms must be smaller than the pores in the
solvent lattice.
– 2. The solute and solvent should have similar
electronegativity.
39
Interstitial Solid Solution

40. (are line defects)
•Dislocations in areas were the atoms are out of position in
the crystal structure. Dislocations are generated and move
when a stress is applied. The motion of dislocations allows
slip – plastic deformation to occur.
• cause slip between crystal plane when they move,
• produce permanent (plastic) deformation.
Dislocations:
Schematic of a
Zinc (HCP):
• before
deformation
• after tensile
elongation
LINE DEFECTS

41. 41
INTERFACIAL DEFECTS
 Interfacial defects are boundaries that have two dimensions and normally separate
regions of the materials that have different crystal structures and/or crystallographic
orientations. These imperfections include external surfaces, grain boundaries, twin
boundaries, stacking faults, and phase boundaries.

42. END
Prep by mequanint. Y
42