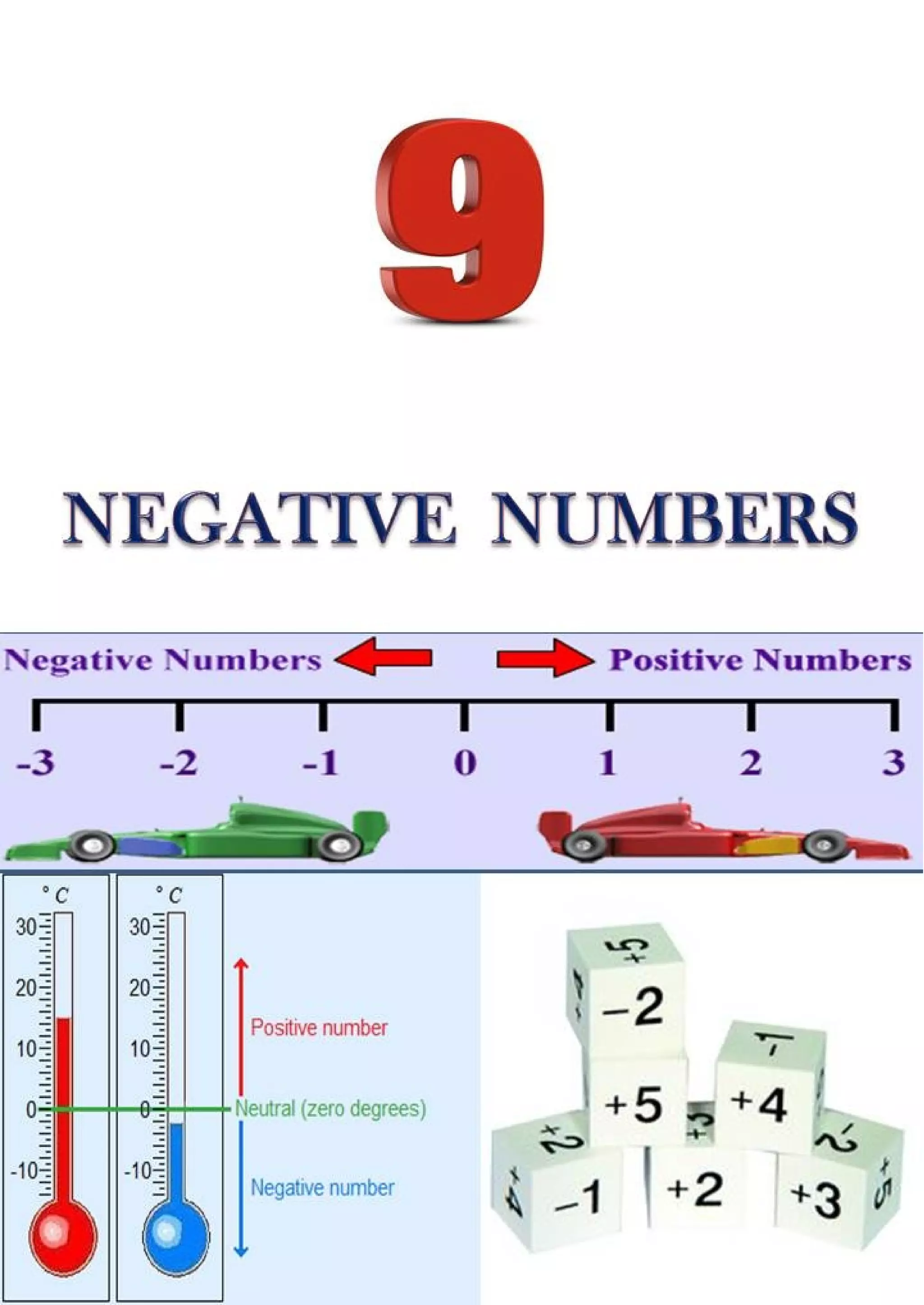
1. The document discusses addition and subtraction of positive and negative numbers through examples. It explains that subtracting a positive number means adding its negative, and vice versa. 2. An equation for the final position of an object is presented as the sum of its initial position and distance traveled. Examples are given of calculating the final position using different starting positions and distances. 3. It is concluded that the equation for calculating the final position based on the initial position and distance traveled holds true for any pair of numbers, positive or negative. Negative solutions were historically considered invalid but are actually correct.

3. What if we take x = -5and y=-3
Like this , we compute
9+(-3) = 9-3 = 6
-9+(-3) = -9-3 = -12
In general we can state as follows:
Adding the negative of a positive number
means subtracting that positive number.
We must also explain the meaning of
subtraction .For example, look at the equation.
z = x-y
If we take x = 12 , y = 7 in this
z = 12-7
If we take x = 7,y = 12,then
z = 7-12 = -5
What if we take x = 12, y = -7?
z = 12-(-7)
What it means?
We can think like this: meaning of 12-7is,what
must be added to 7 to get 12. In other words
7+5=12; and so 12-7=5.
According to this, 12-(-7) means, what must be
added to -7 to get 12.

5. 1. Take a as different positive numbers,
negative numbers and zero, and compute
the following
i. a-(a-2) = 2
ii. 3a-3 = -(3-3a)
iii. (2a+2)-2(a-2) = 4
2. Taking different numbers as x , y and
compute x + y , x – y check whether the
following holds for all numbers
i. 2(x + y) – 2x = 2y
ii. (x + y)-y = x
iii. (x – y)+y = x
iv. (x-y) – x = -y

6. Application
Imagine a car is starting from a point which may
denote by zero and it travels through a straight
road . Let us consider distance to the right by
positive numbers and distance to the left side by
negative numbers. The table given below shows
the travel of the car:
First trip Second trip Final strip
9 meters 2 meters 11 meters
9 meters -2 meters 7 meters
-2 meters 9 meters 7 meters
-9 meters 2 meters -7 meters
2 meters -9 meters -7 meters
-9 meters -2 meters -11 meters
-2 meters -9 meters -11 meters
In each raw of the table , the last number is sum of
first two, isn’t it?
so we can find the final position of the strip by using
the equation

7. We have the general principle ,
for any two positive number, subtracting the
larger from the smaller means , taking the
negative of the smaller subtracting from the
larger.
for any two positive number with
What if is not less than ?
For example, taking
Thus we have
Take other such pairs of numbers as
Don’t we get for all these?
Again should we take as positive numbers
only? For example
Thus the equation is true
here also.
Take other pairs of positive or negative
numbers and check. Doesn’t this equation hold
for that numbers? so this principle is true for all
pairs of numbers.
For a long
time,
negative
solutions
to
problems
were
considere
d "false"