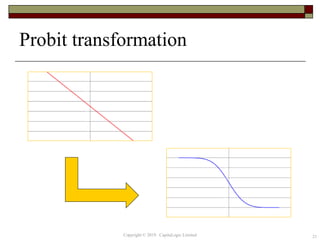
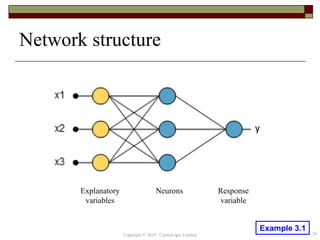
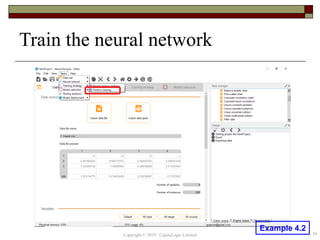
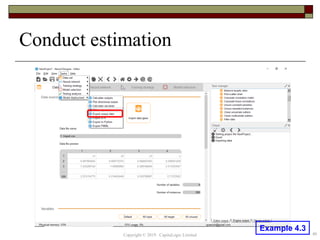
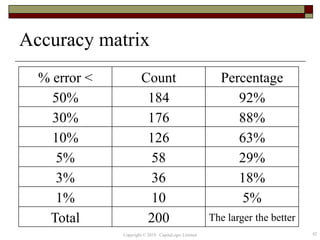
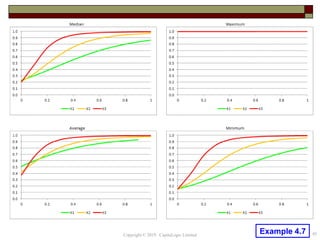
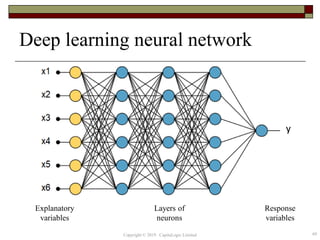
This document provides an overview of credit neural networks and their use in financial risk modeling. It discusses data preparation techniques, classical regression methods like linear and probit regression, monotonic neural networks, and continuous response neural networks. The key aspects covered are data cleaning, variable selection, network structure and training, and accuracy assessment for estimation and out-of-sample testing. The document aims to introduce neural networks as a tool for credit risk analysis and default prediction.