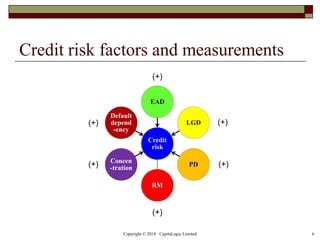
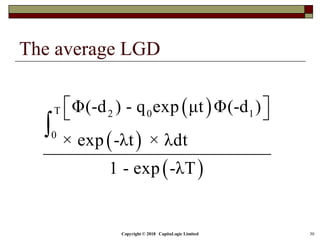This document provides an outline and overview of credit risk controls under the Basel III framework. It discusses controls for both single debts and debt portfolios. For single debts, it describes controls like bilateral netting, principal amortization, collateral, margining, credit guarantees, credit default swaps, downgrade triggers, and call provisions. For debt portfolios, it discusses reducing concentration and dependency through diversification, as well as credit securitization and credit limits. The appendix provides mathematical formulas for concepts like instant LGD, hazard rate, and average LGD.







![Copyright © 2018 CapitaLogic Limited 9
Bilateral netting
Two banks own each other monies
When one bank defaults
Without bilateral netting agreement
Survival bank must surrender the borrowing EAD
immediately to liquidator
Survival bank then collects the lending EAD from
liquidator
EAD = Principal + Accrued interest
With bilateral netting agreement
Net EAD = Max[Lending EAD - Borrowing EAD, 0]
Example 6.1](https://image.slidesharecdn.com/06-181105045409/85/06-2-credit-risk-controls-9-320.jpg)