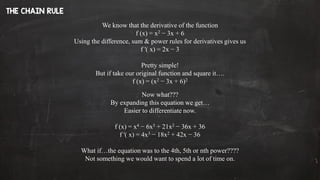The document discusses the chain rule of calculus. The chain rule is used to find the derivative of composite functions, where one function is composed of another function. The derivative of the outer function is taken while leaving the inner function unchanged, then the derivative of the inner function is taken and these are multiplied.

1. THE CHAIN RULE
Basic Calculus:
Quarter 3 –Module 7
G U D I TO, O D ETT E N .
1 1 – LU M I N E SC E NC E

2. THE CHAIN RULE
COMPOSITE FUNCTIONS
They are made up of a function that has a function within it

3. THE CHAIN RULE
The derivative when using the Chain Rule is the derivative of the
outside leaving the inside unchanged times the derivative of the
inside.
𝑦 = 𝑓(𝑔(𝑥))
Inner function
Outer function
𝑑𝑦
𝑑𝑥
= (𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒 𝑜𝑓 𝑡ℎ𝑒 𝑜𝑢𝑡𝑒𝑟 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛) ∙ (𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒 𝑜𝑓 𝑡ℎ𝑒 𝑖𝑛𝑛𝑒𝑟 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛)

4. THE CHAIN RULE
THEOREM
Let f be a function differentiable at c and let g be a function
differentiable at f(c). Then the composition 𝑔 ∘ 𝑓 is differentiable at c and
𝐷𝑥 (𝑔 ∘ 𝑓) (𝑐) = 𝑔 ′ (𝑓(𝑐). 𝑓 ′ (𝑐)

5. The Chain Rule can be written either in the prime notation
(f  g)(x) = f(g(x))  g(x)
or, if y = f(u) and u = g(x), in Leibniz notation:
Equation 3 is easy to remember because if dy/du and du/dx were quotients, then we could
cancel du.
Remember, however, that du has not been defined and du/dx should not be thought of as an
actual quotient.

6. THE CHAIN RULE
STEPS FOR CHAIN RULE
1. Identify inner and outer functions
2. Derive outer function, leaving the inner function alone.
3. Derive the inner function.
4. Multiply the derivative of the outer function and derivative of the inner
function

7. We know that the derivative of the function
f (x) = x2 − 3x + 6
Using the difference, sum & power rules for derivatives gives us
f '( x) = 2x − 3
Pretty simple!
But if take our original function and square it….
f (x) = (x2 − 3x + 6)2
Now what???
By expanding this equation we get…
Easier to differentiate now.
f (x) = x4 − 6x3 + 21x2 − 36x + 36
f '( x) = 4x3 − 18x2 + 42x − 36
What if…the equation was to the 4th, 5th or nth power????
Not something we would want to spend a lot of time on.

8. THE CHAIN RULE

9. Differentiate y = (x3 – 1)100
Taking u = g(x) = x3 – 1 and n = 100
𝒅𝒚
𝒅𝒙
=
𝒅𝒚
𝒅𝒖
.
𝒅𝒖
𝒅𝒙
𝑑𝑦
𝑑𝑥
=
𝑑
𝑑𝑥
(x3 – 1)100
= 100(x3 – 1)99 𝑑
𝑑𝑥
(x3 – 1)
= 100(x3 – 1)99  3x2
= 300x2(x3 – 1)99
E X A M P L E 1 : Po w er Fu n ct i on s

10. THE CHAIN RULE
TRIGONOMETRIC FUNCTION

11. b) Differentiate 𝑦 = cos(𝑥2 − 1).
Let 𝑢 = 𝑥2 − 1 𝑠𝑜 𝑡ℎ𝑎𝑡 𝑦 = cos 𝑢
𝑑𝑢 = 2x
𝑦′ = −sin 𝑢 = − sin(𝑥 2 − 1)
𝒅𝒚
𝒅𝒙
=
𝒅𝒚
𝒅𝒖
.
𝒅𝒖
𝒅𝒙
𝑦′ = −sin(𝑥 2 − 1) ∙ 2x
= −2x 𝐬𝐢𝐧(𝒙2 − 𝟏)
E X A M P L E 2 : Tr igon o m etr i c Fu n ct i on s

12. -
THE CHAIN RULE

13. b) Differentiate 𝑦 = 4x 2 +x
Let 𝑢 = 𝑥2 + x 𝑠𝑜 𝑡ℎ𝑎𝑡 𝑦 = 4𝑢
𝑑𝑢 = 2x + 1
𝑦′ = 4u ln4 = 4x2+x ln4
𝒅𝒚
𝒅𝒙
=
𝒅𝒚
𝒅𝒖
.
𝒅𝒖
𝒅𝒙
𝑦′ = 4x2+x ln4 ∙ (2x+1)
E X A M P L E 3 : E x p on ent i al Fu n ct i on s

14. THE CHAIN RULE
Basic Calculus:
Quarter 3 –Module 7
G U D I TO, O D ETT E N .
1 1 – LU M I N E SC E NC E