Downloaded 10 times
Uploaded bySangjin Han
Large-scale computation without sacrificing expressiveness
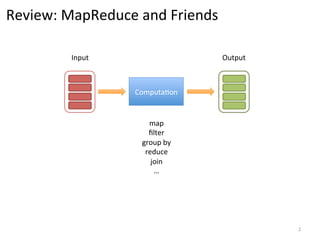
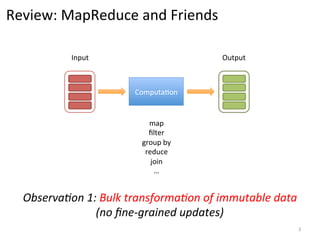
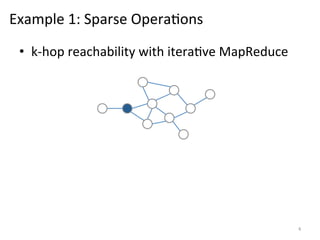
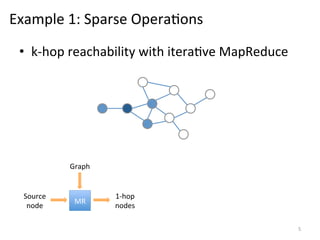
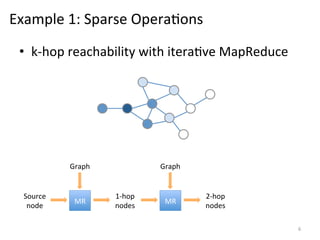
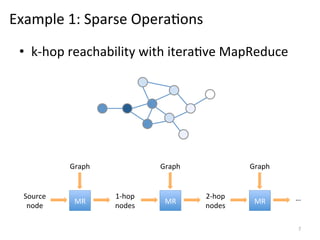
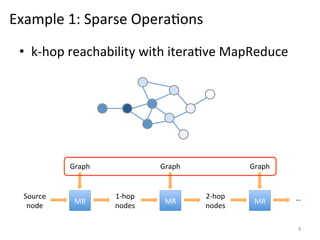
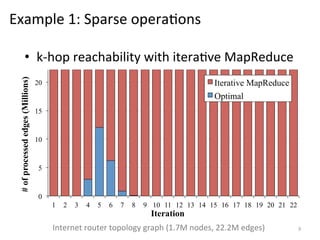
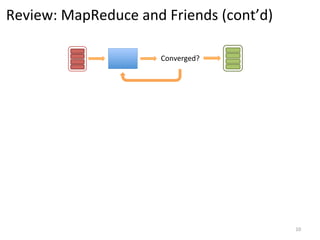
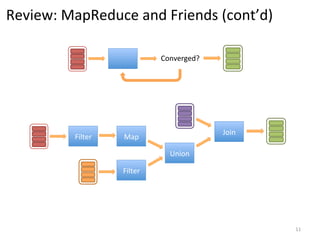
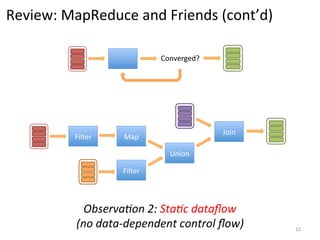
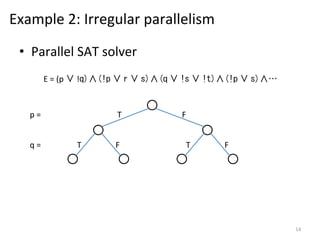
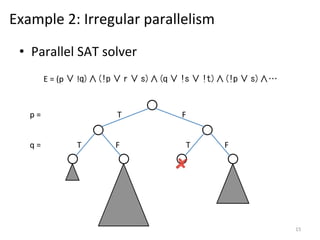
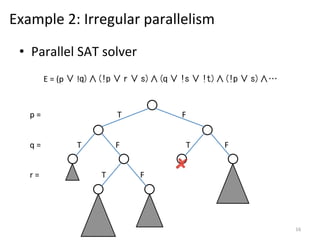
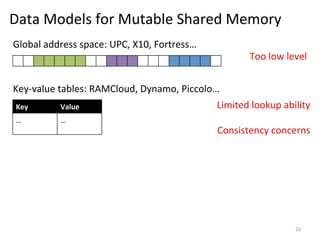
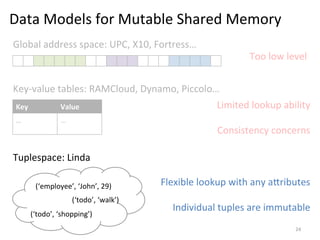
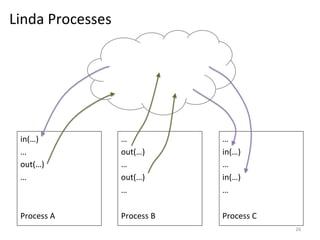
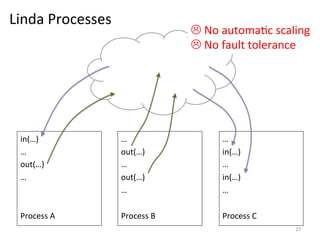
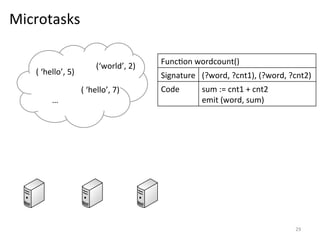
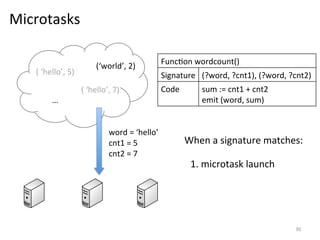
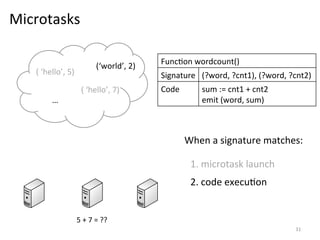
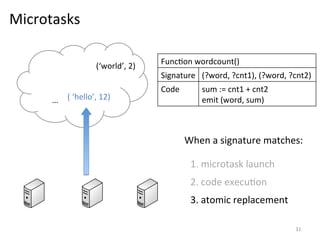
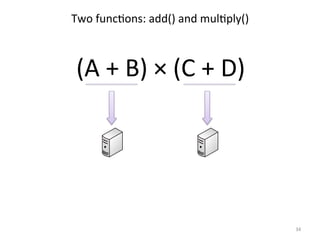
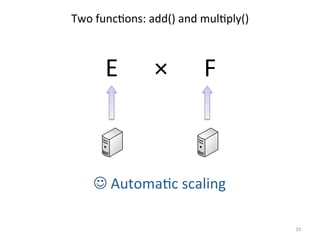
The document discusses the limitations of traditional MapReduce frameworks, particularly in handling sparse and dynamic data operations, and introduces a new programming model called Celias that supports fine-grained operations on mutable data with elastic scalability and fault tolerance. Celias incorporates a tuplespace model and microtasks to enhance expressiveness while maintaining performance. The paper raises questions about the practicality of microtask abstraction and its potential applications.
More Related Content
Similar to Large-scale computation without sacrificing expressiveness
![[Harvard CS264] 03 - Introduction to GPU Computing, CUDA Basics](https://cdn.slidesharecdn.com/ss_thumbnails/cs264201103-cudabasicsshare-110209024624-phpapp02-thumbnail.jpg?width=640&height=640&fit=bounds)
Large-scale computation without sacrificing expressiveness
- 1. Large-‐scale computa0on without sacrificing expressiveness Sangjin Han Sylvia Ratnasamy UC Berkeley 1
- 2. Review: MapReduce and Friends Input Output Computa0on map filter group by reduce join … 2
- 3. Review: MapReduce and Friends Input Output Computa0on map filter group by reduce join … Observa(on 1: Bulk transforma(on of immutable data (no fine-‐grained updates) 3
- 4. Example 1: Sparse Opera0ons • k-‐hop reachability with itera0ve MapReduce 4
- 5. Example 1: Sparse Opera0ons • k-‐hop reachability with itera0ve MapReduce Graph Source node MR 1-‐hop nodes 5
- 6. Example 1: Sparse Opera0ons • k-‐hop reachability with itera0ve MapReduce Graph Source node MR Graph 1-‐hop nodes MR 2-‐hop nodes 6
- 7. Example 1: Sparse Opera0ons • k-‐hop reachability with itera0ve MapReduce Graph Source node MR Graph 1-‐hop nodes MR Graph 2-‐hop nodes MR … 7
- 8. Example 1: Sparse Opera0ons • k-‐hop reachability with itera0ve MapReduce Graph Source node MR Graph 1-‐hop nodes MR Graph 2-‐hop nodes MR … 8
- 9. Example 1: Sparse opera0ons # of processed edges (Millions) • k-‐hop reachability with itera0ve MapReduce Iterative MapReduce Optimal 20 15 10 5 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 Iteration Internet router topology graph (1.7M nodes, 22.2M edges) 9
- 10. Review: MapReduce and Friends (cont’d) Converged? 10
- 11. Review: MapReduce and Friends (cont’d) Converged? Filter Join Map Union Filter 11
- 12. Review: MapReduce and Friends (cont’d) Converged? Filter Join Map Union Filter Observa(on 2: Sta(c dataflow (no data-‐dependent control flow) 12
- 13. Example 2: Irregular parallelism • Parallel SAT solver E = (p ∨ !q)∧(!p ∨ r ∨ s)∧(q ∨ !s ∨ !t)∧(!p ∨ s)∧… 13
- 14. Example 2: Irregular parallelism • Parallel SAT solver E = (p ∨ !q)∧(!p ∨ r ∨ s)∧(q ∨ !s ∨ !t)∧(!p ∨ s)∧… p = T F q = T F T F 14
- 15. Example 2: Irregular parallelism • Parallel SAT solver E = (p ∨ !q)∧(!p ∨ r ∨ s)∧(q ∨ !s ∨ !t)∧(!p ∨ s)∧… p = T F q = T F T F 15
- 16. Example 2: Irregular parallelism • Parallel SAT solver E = (p ∨ !q)∧(!p ∨ r ∨ s)∧(q ∨ !s ∨ !t)∧(!p ∨ s)∧… p = T F q = T F T F r = T F 16
- 17. MapReduce-‐like frameworks assume: 1. Bulk transforma0on of immutable data 2. Sta0c dataflow 17
- 18. Exis0ng frameworks assume: Our work: 1. Bulk transforma0on of immutable data Fine-‐grained opera0ons on mutable data 2. Sta0c dataflow Dynamic, data-‐dependent control flow Yet we s0ll want elas0c scalability and fault tolerance 18
- 19. Spinning a small twist to Linda CELIAS PROGRAMMING MODEL 19
- 20. Programming model = data model + computa0on model 20
- 21. Data Models for Mutable Shared Memory 21
- 22. Data Models for Mutable Shared Memory Global address space: UPC, X10, Fortress… Too low level 22
- 23. Data Models for Mutable Shared Memory Global address space: UPC, X10, Fortress… Too low level Key-‐value tables: RAMCloud, Dynamo, Piccolo… Key Value … … Limited lookup ability Consistency concerns 23
- 24. Data Models for Mutable Shared Memory Global address space: UPC, X10, Fortress… Too low level Key-‐value tables: RAMCloud, Dynamo, Piccolo… Key Value … … Limited lookup ability Consistency concerns Tuplespace: Linda (‘employee’, ‘John’, 29) (‘todo’, ‘walk’) (‘todo’, ‘shopping’) Flexible lookup with any ahributes Individual tuples are immutable 24
- 25. Programming model = data model + computa0on model Linda = Tuplespace + Linda processes 25
- 26. Linda Processes in(…) … out(…) … Process A … out(…) … out(…) … Process B … in(…) … in(…) … Process C 26
- 27. Linda Processes in(…) … out(…) … Process A L No automa0c scaling L No fault tolerance … out(…) … out(…) … Process B … in(…) … in(…) … Process C 27
- 28. Programming model = data model + computa0on model Linda = Tuplespace + Linda processes Celias = Tuplespace + microtasks 28
- 29. Microtasks ( ‘hello’, 5) … (‘world’, 2) ( ‘hello’, 7) Func0on wordcount() Signature (?word, ?cnt1), (?word, ?cnt2) Code sum := cnt1 + cnt2 emit (word, sum) 29
- 30. Microtasks ( ‘hello’, 5) … (‘world’, 2) ( ‘hello’, 7) word = ‘hello’ cnt1 = 5 cnt2 = 7 Func0on wordcount() Signature (?word, ?cnt1), (?word, ?cnt2) Code sum := cnt1 + cnt2 emit (word, sum) When a signature matches: 1. microtask launch 30
- 31. Microtasks ( ‘hello’, 5) … (‘world’, 2) ( ‘hello’, 7) Func0on wordcount() Signature (?word, ?cnt1), (?word, ?cnt2) Code sum := cnt1 + cnt2 emit (word, sum) When a signature matches: 1. microtask launch 2. code execu0on 5 + 7 = ?? 31
- 32. Microtasks (‘world’, 2) … ( ‘hello’, 12) Func0on wordcount() Signature (?word, ?cnt1), (?word, ?cnt2) Code sum := cnt1 + cnt2 emit (word, sum) When a signature matches: 1. microtask launch 2. code execu0on 3. atomic replacement 32
- 33. Two func0ons: add() and mul0ply() (A + B) × (C + D) 33
- 34. Two func0ons: add() and mul0ply() (A + B) × (C + D) 34
- 35. Two func0ons: add() and mul0ply() E × F J Automa0c scaling 35
- 36. Two func0ons: add() and mul0ply() E × F J Automa0c scaling 36
- 37. Two func0ons: add() and mul0ply() E × F J Automa0c scaling 37
- 38. Two func0ons: add() and mul0ply() E × F J Automa0c scaling J Fault tolerance 38
- 39. More Examples in the Paper… • MapReduce – Celias is Turing-‐complete MapReduce-‐complete! – without any ar0ficial sync. barriers • Single-‐source shortest path – Pregel-‐style graph processing • Quicksort – Recursive control flow 39
- 40. Summary • MapReduce-‐like frameworks are not suitable for algorithms with: – Sparse/incremental/fine-‐grained computa0on – Dynamic dataflow • Celias comes to our rescue, yet it is also – automa0cally scalable – fault tolerant 40
- 41. Open Ques0ons • Microtask abstrac0on: good enough? went too far? • Feasibility of an efficient implementa0on – Reliable tuplespace – Signature matching – Microtask transac0ons • … what is a killer app of Celias? • <Your ques0ons here> 41