This document discusses Buss's theories of bounded arithmetic (S2i) and how they relate to the polynomial hierarchy (PH). It proposes using the separation of Buss's theories to approach the separation of levels of PH. It presents a consistency proof for S2i inside S2i+2 by introducing a predicate E for term existence and defining a bounded truth definition. The goal is to separate S2i and S2i+2 through Gödel's incompleteness theorem by showing S2i+2 can prove the i-consistency of S2i-E but S2i cannot prove its own consistency. Future work aims to simplify S2i-E and formally prove S2i can derive the i

1. Bounded Arithmetic in Free Logic
Yoriyuki Yamagata
CTFM, 2013/02/20

2. Buss’s theories 𝑆2𝑖
–a#b=2 𝑎 ⋅|𝑏|
• Language of Peano Arithmetic + “#”
• BASIC axioms
𝑥
𝐴 , Γ → Δ, 𝐴(𝑥)
2
• PIND
𝐴 0 , Γ → Δ, 𝐴(𝑡)
where 𝐴 𝑥 ∈ Σ 𝑖𝑏 , i.e. has 𝑖-alternations of
bounded quantifiers ∀𝑥 ≤ 𝑡, ∃𝑥 ≤ 𝑡.

3. PH and Buss’s theories 𝑆2𝑖
𝑆2 = 𝑆2 = 𝑆2 = …
1 2 3
𝑃 = □(𝑁𝑁) = □(Σ2 ) = …
𝑝
Implies
We can approach (non) collapse of PH from
(non) collapse of hierarchy of Buss’s theories
(PH = Polynomial Hierarchy)

4. Our approach
• Separate 𝑆2𝑖 by Gödel incompleteness theorem
• Use analogy of separation of 𝐼Σ 𝑖

5. Separation of 𝐼Σ 𝑖
𝐼Σ3 ⊢ Con(IΣ2 )
…
𝐼Σ2 ⊢ Con IΣ2
⊆
𝐼Σ1
⊆

6. Consistency proof inside 𝑆2𝑖
• Bounded Arithmetics generally are not
– 𝑆2 does not prove consistency of Q (Paris, Wilkie)
capable to prove consistency.
– 𝑆2 does not prove bounded consistency of
𝑆2 (Pudlák)
1
– 𝑆2 does not prove consistency the 𝐵 𝑖 𝑏 fragement
𝑖
of 𝑆2 (Buss and Ignjatović)
−1

7. Buss and Ignjatović(1995)
…𝑆2 ⊢ 𝐵3 − Con(𝑆2 )
3 b −1
𝑆2
2
⊢ 𝐵2
b
− Con(𝑆2 )
−1
⊆
𝑆2
1
⊢ 𝐵1
b
− Con(𝑆2 )
−1
⊆

8. Where…
• 𝐵 𝑖 𝑏 − 𝐶𝐶𝐶 𝑇
– consistency of 𝐵 𝑖 𝑏 −proofs
– 𝐵 𝑖 𝑏 −proofs : the proofs by 𝐵 𝑖 𝑏 -formule
– 𝐵 𝑖 𝑏 :Σ0𝑏 (Σ 𝑖𝑏 )… Formulas generated from Σ 𝑖𝑏 by
Boolean connectives and sharply bounded
• 𝑆2
−1
quantifiers.
– Induction free fragment of 𝑆2𝑖

9. If…
𝑆2 ⊢ 𝐵i − Con 𝑆2 ,j > i
𝑗 b −1
Then, Buss’s hierarchy does not collapse.

10. Consistency proof of 𝑆2 inside 𝑆2𝑖
−1
Problem
• No truth definition, because
• No valuation of terms, because
• The values of terms increase exponentially
In 𝑆2 world, terms do not have values a priori.
𝑖
• E.g. 2#2#2#2#2#...#2
• We introduce the predicate 𝐸 which signifies existence of
• Thus, we must prove the existence of values in proofs.
values.

11. Our result(2012)
𝑆2
…5
⊢3− Con(𝑆2
−1
𝐸)
𝑆2
4
⊢2− Con(𝑆2
−1
𝐸)
⊆
𝑆2
3
⊢1− Con(𝑆2
−1
𝐸)
⊆

12. Where…
• 𝑖 − 𝐶𝐶𝐶 𝑇
– consistency of 𝑖-normal proofs
– 𝑖-normal proofs : the proofs by 𝑖-normal formulas
– 𝑖-normal formulas: Formulas in the form:
∃𝑥1 ≤ 𝑡1 ∀𝑥2 ≤ 𝑡2 … 𝑄𝑥 𝑖 ≤ 𝑡 𝑖 𝑄𝑥 𝑖+1 ≤ 𝑡 𝑖+1 . 𝐴(… )
Where 𝐴 is quantifier free

13. Where…
• 𝑆2 𝐸
−1
– Induction free fragment of 𝑆2 𝐸
𝑖
– have predicate 𝐸 which signifies existence of
values
• Such logic is called Free logic

14. 𝑆2𝑖
𝐸(Language)
• =, ≤, 𝐸
Predicates
Function symbols
• Finite number of polynomial functions
Formulas
• 𝐴 ∨ 𝐵, 𝐴 ∧ 𝐵
• Atomic formula, negated atomic formula
• Bounded quantifiers

15. 𝑆2𝑖
𝐸(Axioms)
• 𝐸-axioms
• Equality axioms
• Data axioms
• Defining axioms
• Auxiliary axioms

16. Idea behind axioms…
→ 𝑎= 𝑎
Because there is no guarantee of 𝐸𝐸
Thus, we add 𝐸𝐸 in the antecedent
𝐸𝐸 → 𝑎 = 𝑎

17. E-axioms
• 𝐸𝐸 𝑎1 , … , 𝑎 𝑛 → 𝐸𝑎 𝑗
• 𝑎1 = 𝑎2 → 𝐸𝑎 𝑗
• 𝑎1 ≠ 𝑎2 → 𝐸𝑎 𝑗
• 𝑎1 ≤ 𝑎2 → 𝐸𝑎 𝑗
• ¬𝑎1 ≤ 𝑎2 → 𝐸𝑎 𝑗

18. Equality axioms
• 𝐸𝐸 → 𝑎 = 𝑎
• 𝐸𝐸 ⃗ , ⃗ = 𝑏 → 𝑓 ⃗ = 𝑓 𝑏
𝑎 𝑎 𝑎

19. Data axioms
• → 𝐸𝐸
• 𝐸𝐸 → 𝐸𝑠0 𝑎
• 𝐸𝐸 → 𝐸𝑠1 𝑎

20. Defining axioms
𝑓 𝑢 𝑎1 , 𝑎2 , … , 𝑎 𝑛 = 𝑡(𝑎1 , … , 𝑎 𝑛 )
𝑢 𝑎 = 0, 𝑎, 𝑠0 𝑎, 𝑠1 𝑎
𝐸𝑎1 , … , 𝐸𝑎 𝑛 , 𝐸𝐸 𝑎1 , … , 𝑎 𝑛 →
𝑓 𝑢 𝑎1 , 𝑎2 , … , 𝑎 𝑛 = 𝑡(𝑎1 , … , 𝑎 𝑛 )

21. Auxiliary axioms
𝑎 = 𝑏 ⊃ 𝑎#𝑐 = 𝑏#𝑐
𝐸𝐸#𝑐, 𝐸𝐸#𝑐, 𝑎 = |𝑏| → 𝑎#𝑐 = 𝑏#𝑐

22. PIND-rule
where 𝐴 is an Σ 𝑖𝑏 -formulas

23. Bootstrapping 𝑆2𝑖
𝐸
I. 𝑆2 𝐸 ⊢ Tot(𝑓) for any 𝑓, 𝑖 ≥ 0
𝑖
II. 𝑆2 𝐸 ⊢ BASIC∗ , equality axioms
𝑖 ∗
III. 𝑆2 𝐸 ⊢ predicate logic
𝑖 ∗
IV. 𝑆2𝑖
𝐸⊢ Σ𝑖𝑏
−PIND∗

24. Theorem (Consistency)
𝑆2𝑖+2
⊢i− Con(𝑆2
−1
𝐸)

25. Valuation trees
ρ-valuation tree bounded by 19
ρ(a)=2, ρ(b)=3
a=2
a#a=16 b=3
𝑣 𝑎#𝑎 + 𝑏 , 𝜌 ↓19 19
a#a+b=19
𝑣 𝑡 , 𝜌 ↓ 𝑢 𝑐 is Σ1𝑏

26. Bounded truth definition (1)
• 𝑇 𝑢, 𝑡1 = 𝑡2 , 𝜌 ⇔def
∃𝑐 ≤ 𝑢, 𝑣 𝑡1 , 𝜌 ↓ 𝑢 𝑐 ∧ 𝑣 𝑡1 , 𝜌 ↓ 𝑢 𝑐
• 𝑇 𝑢, 𝜙1 ∧ 𝜙2 , 𝜌 ⇔def
𝑇 𝑢, 𝜙1 , 𝜌 ∧ 𝑇 𝑢, 𝜙2 , 𝜌
• 𝑇 𝑢, 𝜙1 ∨ 𝜙2 , 𝜌 ⇔def
𝑇 𝑢, 𝜙1 , 𝜌 ∨ 𝑇 𝑢, 𝜙2 , 𝜌

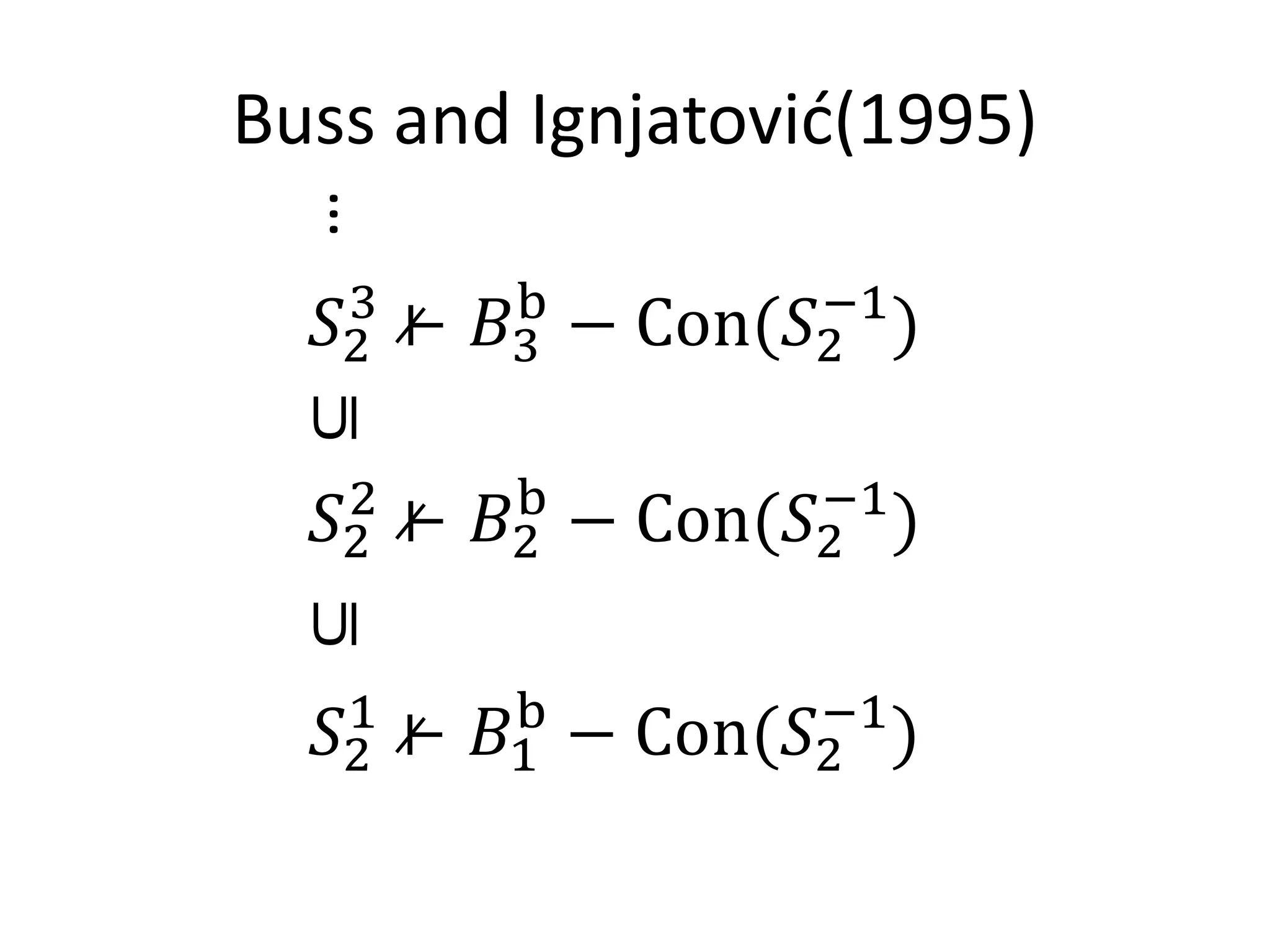
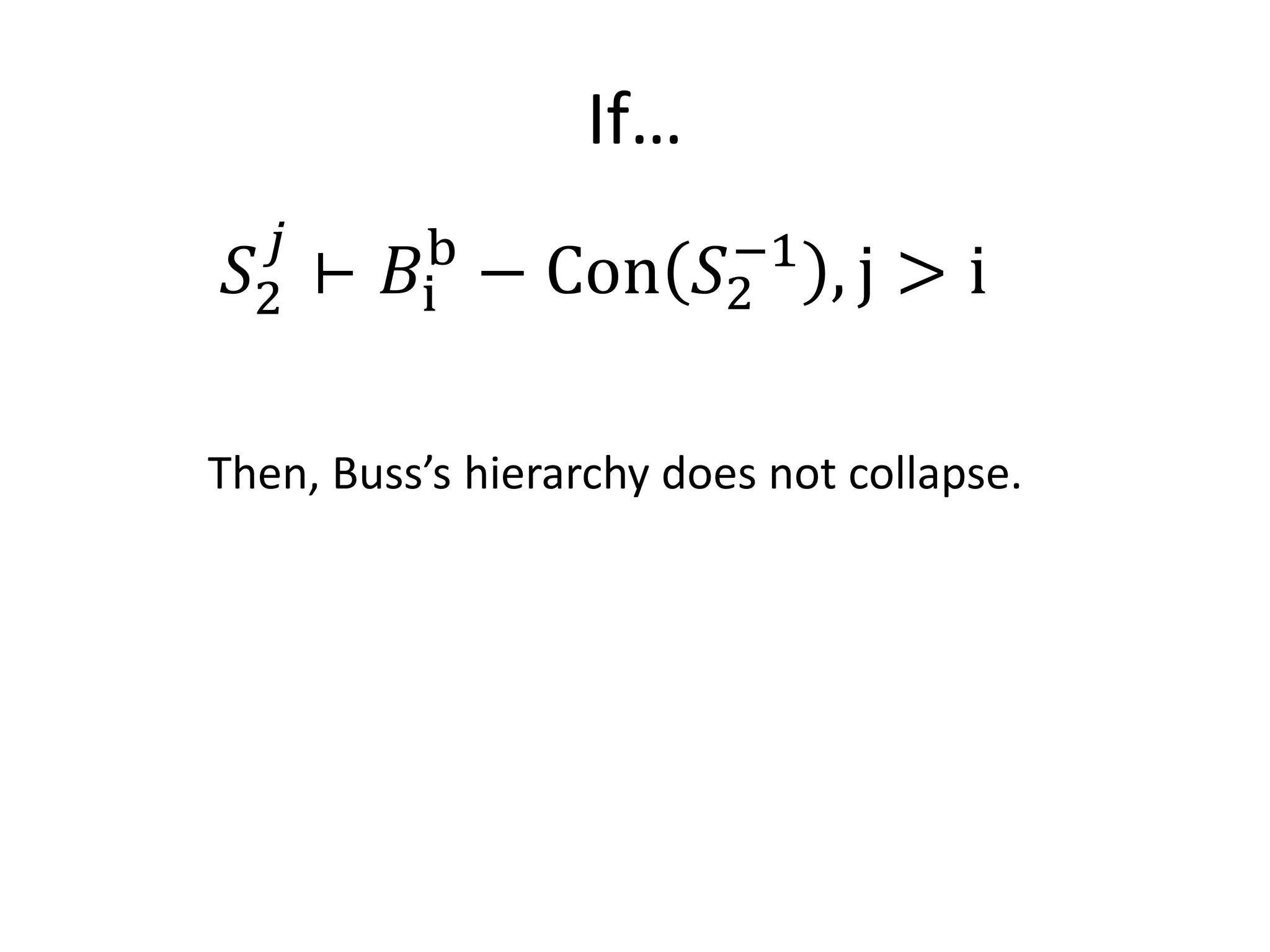
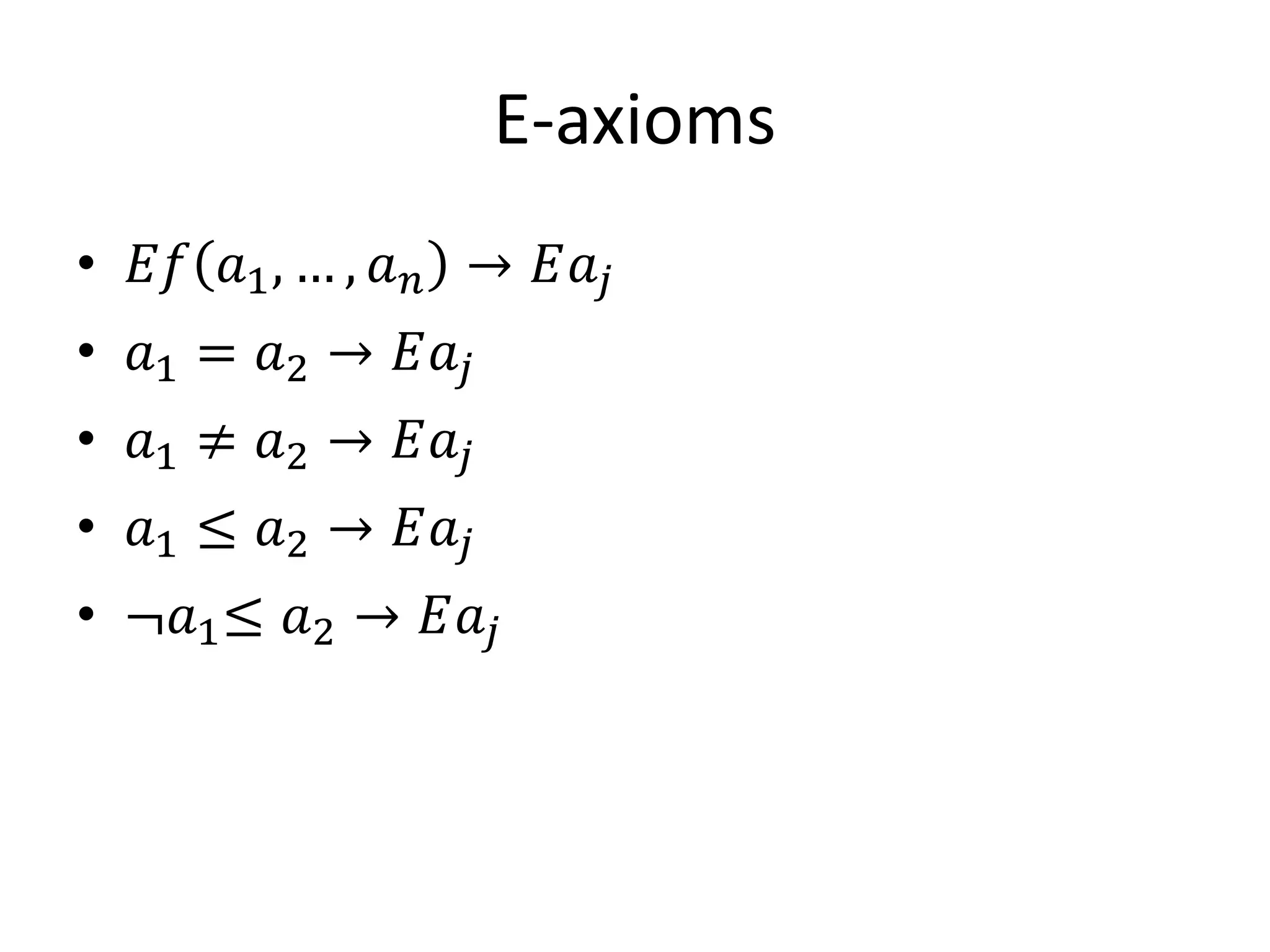
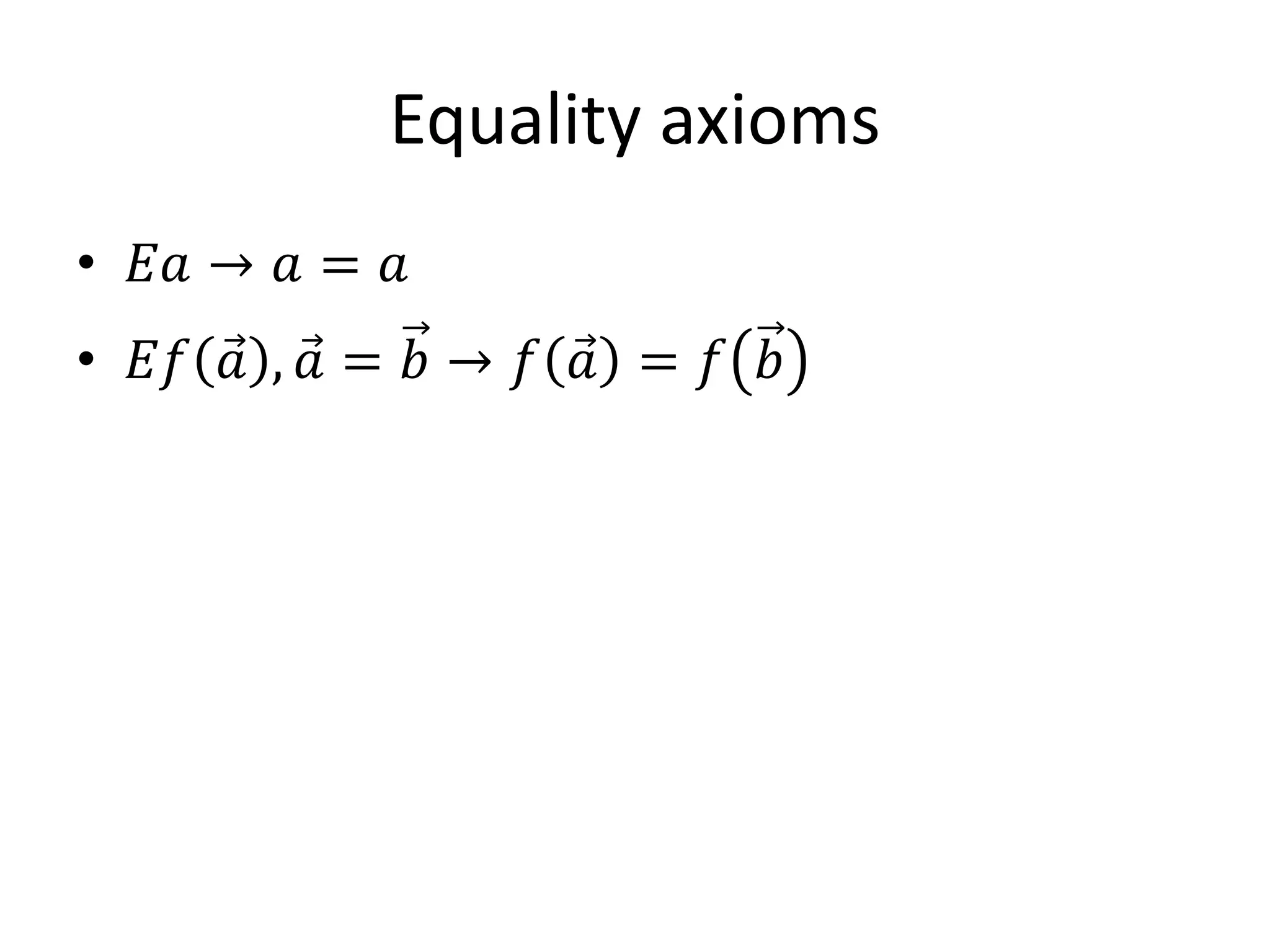
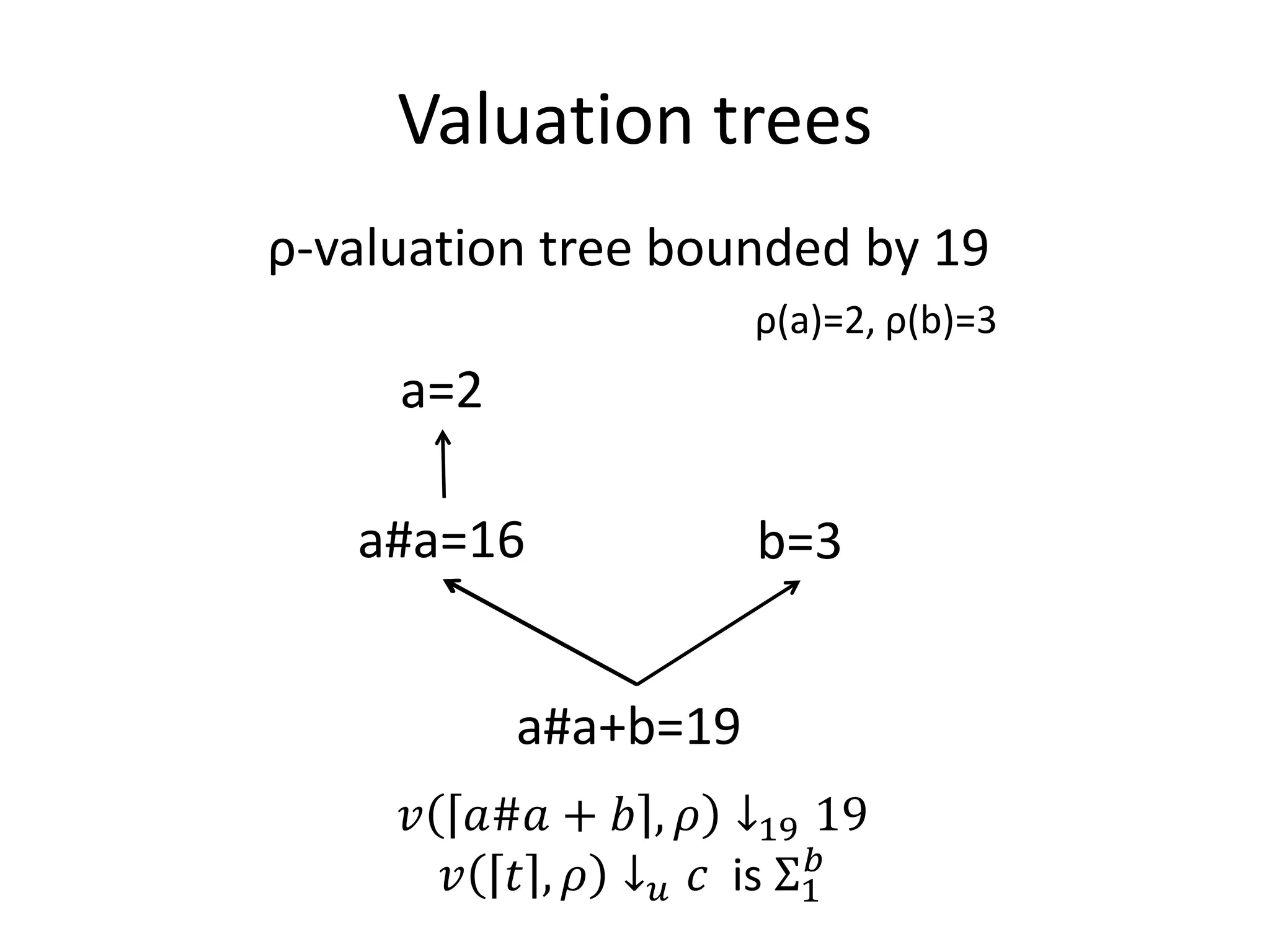
27. Bounded truth definition (2)
• 𝑇 𝑢, ∃𝑥 ≤ 𝑡, 𝜙(𝑥) , 𝜌 ⇔def
∃𝑐 ≤ 𝑢, 𝑣 𝑡 , 𝜌 ↓ 𝑢 𝑐 ∧
∃𝑑 ≤ 𝑐, 𝑇 𝑢, 𝜙 𝑥 , 𝜌 𝑥 ↦ 𝑑
• 𝑇 𝑢, ∀𝑥 ≤ 𝑡, 𝜙(𝑥) , 𝜌 ⇔def
∃𝑐 ≤ 𝑢, 𝑣 𝑡 , 𝜌 ↓ 𝑢 𝑐 ∧
∀𝑑 ≤ 𝑐, 𝑇(𝑢, 𝜙 𝑥 , 𝜌[𝑥 ↦ 𝑑])
Remark: If 𝜙 is Σ 𝑖𝑏 , 𝑇 𝑢, 𝜙 is Σ 𝑖+1
𝑏

28. induction hypothesis
𝑢: enough large integer
𝑟: node of a proof of 0=1
Γ 𝑟 → Δ 𝑟 : the sequent of node 𝑟
𝜌: assignment 𝜌 𝑎 ≤ 𝑢
∀𝑢′ ≤ 𝑢 ⊖ 𝑟, { ∀𝐴 ∈ Γ 𝑟 𝑇 𝑢′ , 𝐴 , 𝜌 ⊃
[∃𝐵 ∈ Δr , 𝑇(𝑢′ ⊕ 𝑟, 𝐵 , 𝜌)]}

29. Conjecture
𝑆2
−1
𝐸 is weak enough
– 𝑆2 can prove 𝑖-consistency of 𝑆2 𝐸
•
𝑖+2 −1
• While 𝑆2 𝐸 is strong enough
−1
– 𝑆2 𝐸 can interpret 𝑆2
𝑖 𝑖
𝑆2 𝐸 is a good candidate to separate 𝑆2 and 𝑆2 .
• Conjecture
−1 𝑖 𝑖+2

30. Future works
𝑆2 ⊢ 𝑖−Con(𝑆2 𝐸)?
𝑖 −1
• Long-term goal
– Simplify 𝑆2 𝐸
• Short-term goal
𝑖

31. Publications
• Bounded Arithmetic in Free Logic
Logical Methods in Computer Science
Volume 8, Issue 3, Aug. 10, 2012