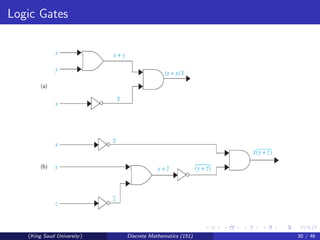
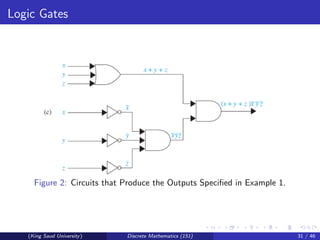
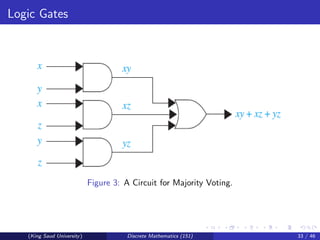
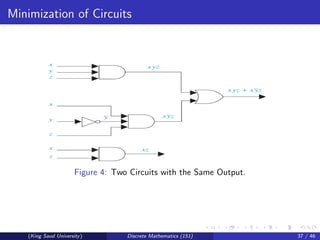
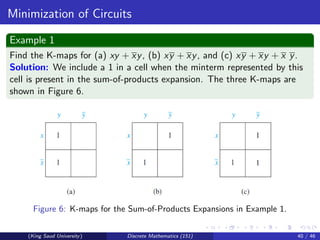
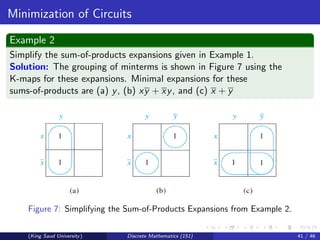
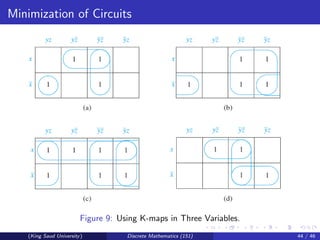
This document discusses Boolean algebra and Boolean functions. It covers topics like Boolean operations, Boolean expressions, identities in Boolean algebra, and representing Boolean functions. Specifically, it shows that any Boolean function can be represented by a Boolean sum of Boolean products of the variables and their complements. It also introduces the concept of duality and defines a Boolean algebra in abstract terms.