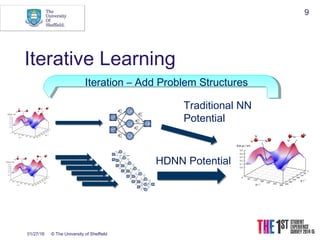
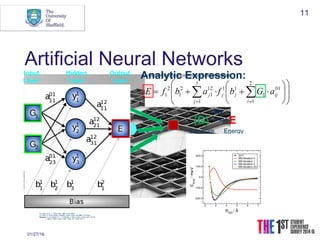
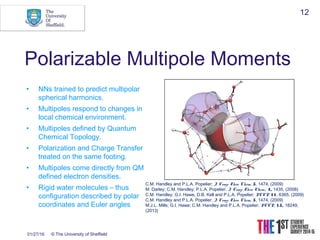
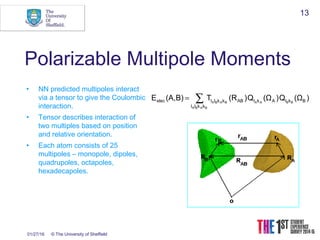
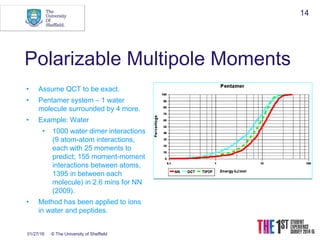
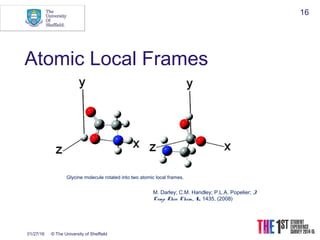
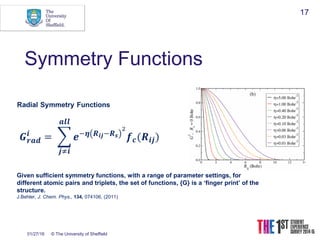
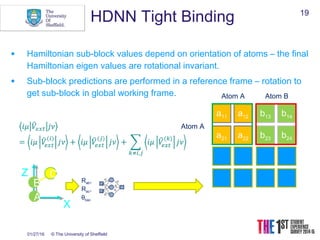
This document discusses using neural networks to represent potential energy surfaces for chemical simulations. It begins by introducing machine learning and how neural networks can be used for functional form discovery and interpolation. It then discusses limitations of traditional computational chemistry methods and force fields. Neural networks are presented as a way to achieve ab initio accuracy at a lower computational cost by training networks on ab initio data. The document outlines different types of neural networks that have been applied for this purpose, including those representing multipole moments and high dimensional neural networks invariant to translations and rotations. It concludes by discussing future directions, such as networks that better retain quantum information and more powerful machine learning methods.

1. Neural Networks for
Chemical Simulations
A Machine Learning solution for Potential
Energy Surface Representation
Chris Handley
N8 HPC – York 8/01/16

2. 01/27/16 © The University of Sheffield
2
Contents
• Why Machine Learning for Chemical
Simulation?
• What is a Neural Network?
• Early Applications of Neural Networks
• High Dimensional Neural Networks?
• Future Advances

3. 01/27/16 © The University of Sheffield
3
Machine Learning
• Many methods for finding non-linear
relationships between some input and outputs.
• Used for functional form discovery –
interpolation, extrapolation.
• Also used for classification of things.
• Classic examples – optical character recognition,
speech analysis.

4. 01/27/16 © The University of Sheffield
4
Computational Chemistry
The underlying physical laws necessary for the mathematical theory of a large
part of physics and the whole of chemistry are thus completely known,
and the difficulty is only that the exact application of
these laws leads to equations much too complicated to be
soluble. It therefore becomes desirable that approximate
practical methods of applying quantum mechanics should
be developed, which can lead to an explanation of the main features of
complex atomic systems without too much computation.
Paul Dirac -
Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathem
(6 April 1929)

5. 01/27/16 © The University of Sheffield
5
Computational Chemistry
An increase in computer power of at least two orders of magnitude
should occur over the next decade. Without further research into the
accuracy of force-field potentials, future macromolecular modeling may well be
limited more by validity of the energy functions, particularly electrostatic
terms, than by technical ability to perform the computations.
Force fields for protein simulations
JW Ponder, DA Case - Advances in protein chemistry, 2003

6. 01/27/16 © The University of Sheffield
6
Computational Chemistry
• Ab Initio methods – Hartree Fock and post-Hartree
Fock methods, DFT. – Expensive for large
systems.
• Tight Binding, Bond Order Potentials.
• Classical “Newtonian” simulations. – Fast, deal with
larger systems, but lack of chemical realism.
The “Jacob’s Ladder” to exact chemical accuracy.

7. 01/27/16 © The University of Sheffield
7
Classical Chemical Force Fields
• Energy is composed of;
• Bond stretching
• Angle Bending
• Torsional rotation
• Electrostatic interactions
• Lennard Jones potential to represent long range
attraction and close range repulsion
• All of these have simple functional forms

8. 01/27/16 © The University of Sheffield
8
The ideal goal
• Ab Initio accuracy at the cost of tradition force
fields/molecular dynamics.
• Neural Networks are trained to discover the
potential energy surfaces.
• Neural Networks are presented a number of Ab
Initio training examples.
• Neural Networks are able to interpolate.

9. 01/27/16 © The University of Sheffield
9
Iterative Learning
Traditional NN
Potential
HDNN Potential
Iteration – Add Problem Structures

10. 01/27/16 © The University of Sheffield
10
Neural Networks
• A computational tool based upon
biological neurons.
• A neuron, takes a signal, or
collection of signals, and if a
threshold is met, it activates.
• On activation the neuron generates
a signal it passes on.

11. 01/27/16
T.B. Blank et al., J. Chem. Phys. 103, 4129 (1995).
S. Lorenz, A. Groß, and M. Scheffler, Chem. Phys. Lett. 395, 210 (2004).
Reviews: C. M. Handley, P. L. A. Popelier, J. Phys. Chem. A 114, 3371 (2010).
J. Behler, Phys. Chem. Chem. Phys. 13, 17930 (2011).
11
Artificial Neural Networks
Input
Layer
Hidden
Layer
Output
Layer
Analytic Expression:
{G} → E
Structure Energy
NN

12. 01/27/16 © The University of Sheffield
12
Polarizable Multipole Moments
• NNs trained to predict multipolar
spherical harmonics.
• Multipoles respond to changes in
local chemical environment.
• Multipoles defined by Quantum
Chemical Topology.
• Polarization and Charge Transfer
treated on the same footing.
• Multipoles come directly from QM
defined electron densities.
• Rigid water molecules – thus
configuration described by polar
coordinates and Euler angles
C.M. Handley and P.L.A. Popelier; J. Comp. Theo. Chem., 5, 1474, (2009)
M. Darley; C.M. Handley; P.L.A. Popelier; J. Comp. Theo. Chem., 4, 1435, (2008)
C.M. Handley; G.I. Hawe, D.B. Kell and P.L.A. Popelier; PCCP, 11, 6365, (2009)
C.M. Handley and P.L.A. Popelier; J. Comp. Theo. Chem., 5, 1474, (2009)
M.J.L. Mills; G.I. Hawe; C.M. Handley and P.L.A. Popelier; PCCP, 15, 18249,
(2013)

13. 01/27/16 © The University of Sheffield
13
Polarizable Multipole Moments
• NN predicted multipoles interact
via a tensor to give the Coulombic
interaction.
• Tensor describes interaction of
two multiples based on position
and relative orientation.
• Each atom consists of 25
multipoles – monopole, dipoles,
quadrupoles, octapoles,
hexadecapoles.
)(ΩQ)(ΩQ)(RTB)(A,E Bkl
kkll
AklABkkllelec BB
BABA
AABABA∑=

14. 01/27/16 © The University of Sheffield
14
Polarizable Multipole Moments
• Assume QCT to be exact.
• Pentamer system – 1 water
molecule surrounded by 4 more.
• Example: Water
• 1000 water dimer interactions
(9 atom-atom interactions,
each with 25 moments to
predict; 155 moment-moment
interactions between atoms,
1395 in between each
molecule) in 2.6 mins for NN
(2009).
• Method has been applied to ions
in water and peptides.

15. 01/27/16 © The University of Sheffield
15
Dimensionality Problem
• Early examples used Cartesian coordinates wrt
a particular frame e.g. a surface and active site.
• Internal Coordinate can be used.
• But…. Ideally we want a method invariant to
translation, rotation, and takes advantage of the
symmetry of the system.

16. 01/27/16 © The University of Sheffield
16
Atomic Local Frames
Glycine molecule rotated into two atomic local frames.
M. Darley; C.M. Handley; P.L.A. Popelier; J.
Comp. Theo. Chem., 4, 1435, (2008)

17. 01/27/16 © The University of Sheffield
17
Symmetry Functions
Given sufficient symmetry functions, with a range of parameter settings, for
different atomic pairs and triplets, the set of functions, {G} is a ‘finger print’ of the
structure.
J.Behler, J. Chem. Phys., 134, 074106, (2011)

18. 01/27/16 © The University of Sheffield
18
HDNN – High Dimensional Neural
Networks
J. Behler and M. Parrinello, Phys. Rev. Lett. 98,
146401 (2007).
J. Behler, J. Chem. Phys. 134, 074106 (2011).
N. Artrith, T. Morawietz and J. Behler, Phys. Rev. B
83, 153101 (2011).
T. Morawietz, V. Sharma and J. Behler, J. Chem.
Phys. 136, 064103 (2012).

19. 01/27/16 © The University of Sheffield
19
HDNN Tight Binding
• Hamiltonian sub-block values depend on orientation of atoms – the final
Hamiltonian eigen values are rotational invariant.
• Sub-block predictions are performed in a reference frame – rotation to
get sub-block in global working frame.
a11 a12
a21 a22
b13 b14
b23 b24
Atom A Atom B
Atom A
CZ
X
Rab,
Rac,
θbacA
B

20. 01/27/16 © The University of Sheffield
20
The Future?
• PES that better retain information from the quantum
mechanical training data e.g. prediction of Tight Binding
Hamiltonians (on going at RUB).
• More powerful machine learning methods e.g. Support
Vector Machines, Gaussian Process Regression.†
• Building force fields that are able to cope with many
molecular, and solid state, systems.
† C.M. Handley and J. Behler; “Next Generation Interatomic Potentials for Condensed Phase
Systems”, The European Physical Journal B, 87, 1-16, (2014)

21. 01/27/16 © The University of Sheffield
21
Thanks
• Popelier Group – Manchester
• Paul Popelier
• Matt Mills
• Glenn Hawe
• Behler Group – RUB, Germany
• Jörg Behler
• Nong Artrith
• Tobias Morawietz

22. Questions?