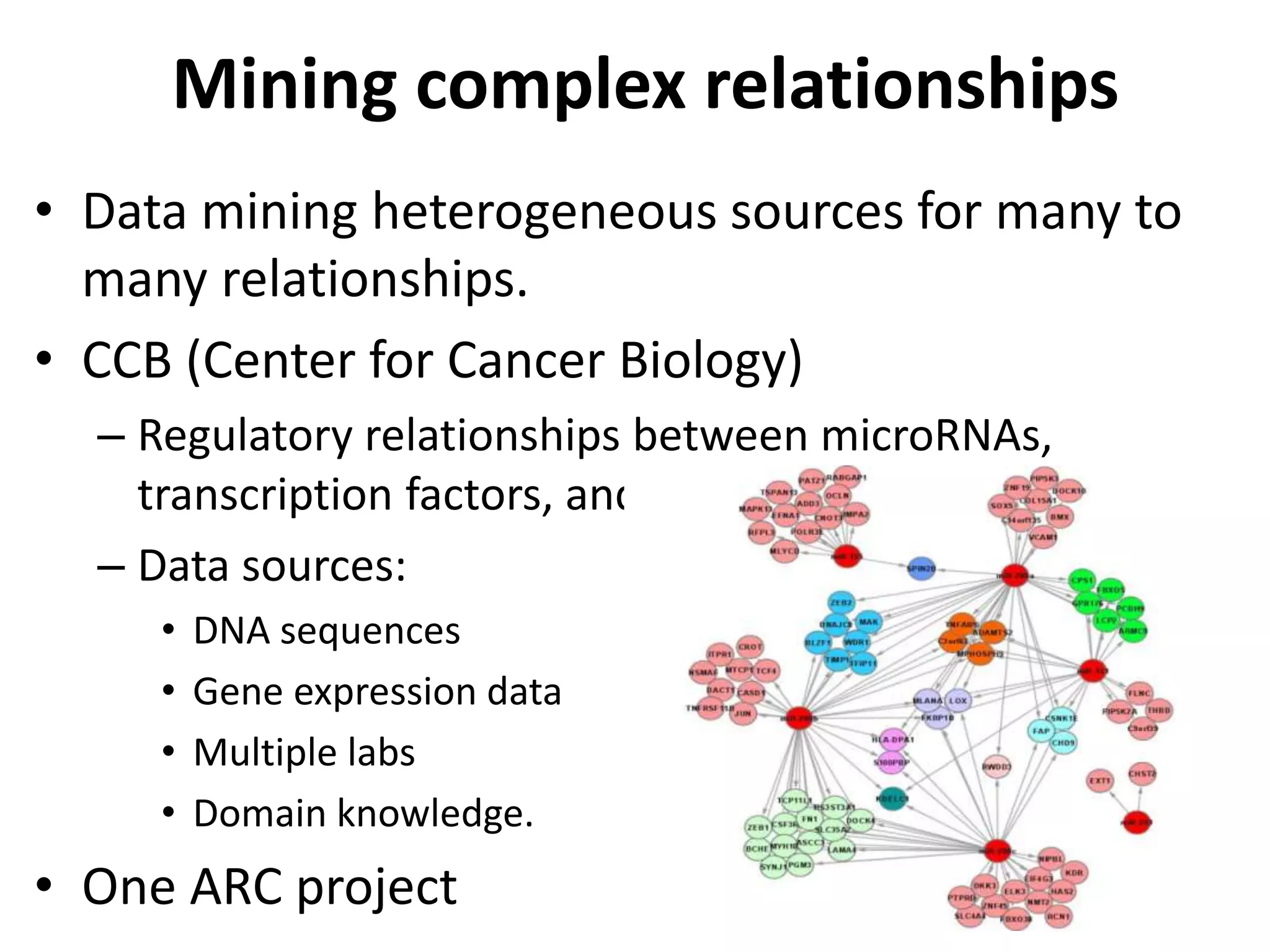
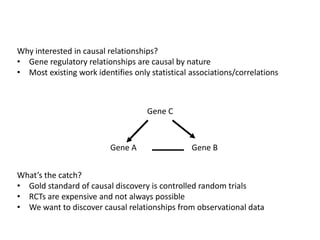
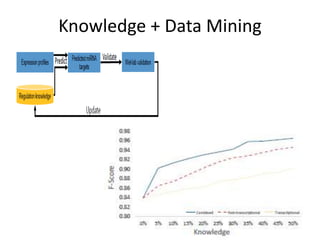
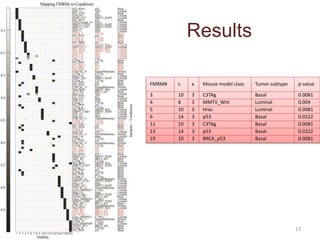
This document discusses mining complex relationships between microRNAs, transcription factors, and genes from heterogeneous data sources using causal inference approaches. Specifically, it describes a project that aims to infer regulatory relationships between microRNAs and mRNAs from multiple data sources including DNA sequences, gene expression data, and domain knowledge. It also discusses using causal inference methods like IDA to detect condition-specific regulatory relationships by analyzing samples split according to normal or cancer conditions.

1. Mining complex relationships
• Data mining heterogeneous sources for many to
many relationships.
• CCB (Center for Cancer Biology)
– Regulatory relationships between microRNAs,
transcription factors, and genes.
– Data sources:
• DNA sequences
• Gene expression data
• Multiple labs
• Domain knowledge.
• One ARC project

2. • Causal inference
• Discovery of group-group relationships
Heterogeneous data
Inferring miRNA-mRNA regulatory relationships
Gene regulatory relationships

3. Causal inference based approaches
Why interested in causal relationships?
• Gene regulatory relationships are causal by nature
• Most existing work identifies only statistical associations/correlations
Gene C
Gene A Gene B
What’s the catch?
• Gold standard of causal discovery is controlled random trials
• RCTs are expensive and not always possible
• We want to discover causal relationships from observational data

4. Causal inference– Do calculus
Judea Pearl. Causality: Models, Reasoning, and Inference. Cambridge University Press, 2000.
X1 X2 … Xn-1 Xn
5.2 7.5 6.5 5.2
5.6 7.2 6.6 5.3
… … … … …
5.4 7.1 7.1 5.7
5.7 6.9 6.9 5.8
+1
+0.8

5. Methods
– IDA
– Maathuis, H. M.,
Colombo, D., Kalisch, M.,
and Buhlmann, P. (2010).
Predicting causal effects
in large-scale systems
from observational data.
Nature Methods, 7(4),
247–249.
5

6. 6

7. Causal inference based approaches
• We also applied the causal inference method to
detect condition specific regulatory relationships
• The steps:
˗ Split samples into to two parts according to conditions
(cancer or normal)
˗ Detect causal regulatory relationships in each condition
˗ A relationship (miR_i, mR_j) detected in condition 1 but
not in condition 2 is specific to condition 1, and miR_i is
an active microRNA in condition 1

8. Causal inference based approaches

9. Knowledge + Data Mining

10. Idea from information retrieval
• Correspondence Latent Dirichlet Allocation
(Corr-LDA)
– Automatic annotations of images (Blei et al.
2004)

11. images
words
miRNAs
mRNAs
Model migration
11
FMRMs DependencyTopics
FMRMs

12. Generative process
12
• Each miRNA or mRNA is drawn from one of the
modules;
• Each sample is a random mixture of miRNAs and
mRNAs expressed in different modules;
• Samples may associate with multiple functional
modules;

13. Results
13
FMRM# c x Mouse model class Tumor subtype p-value
3 10 3 C3TAg Basal 0.0081
4 8 3 MMTV_Wnt Luminal 0.004
5 10 3 Hras Luminal 0.0081
6 14 3 p53 Basal 0.0222
11 10 3 C3TAg Basal 0.0081
13 14 3 p53 Basal 0.0222
19 10 3 BRCA_p53 Basal 0.0081

14. Causal inference based approaches

15. Causal inference based approaches