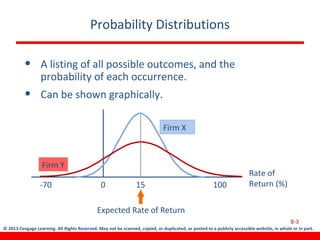
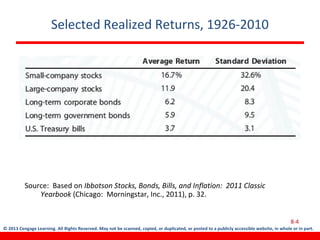
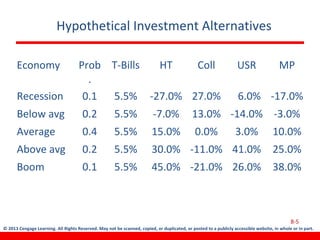
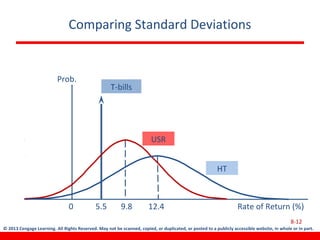
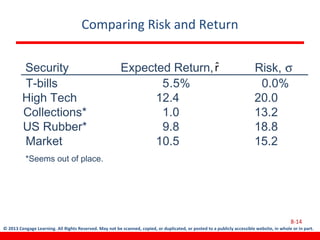
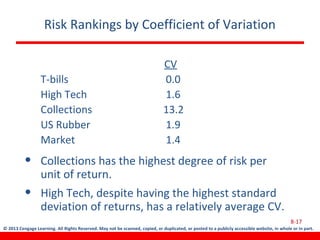
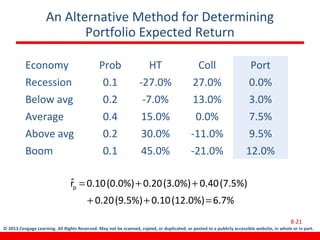
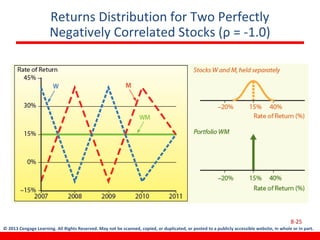
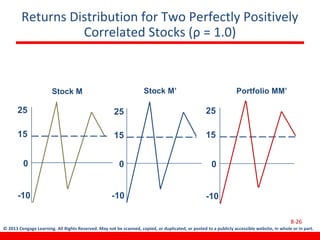
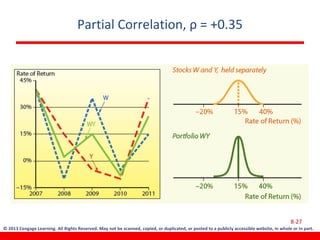
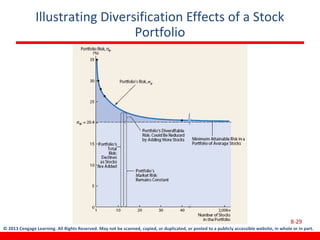
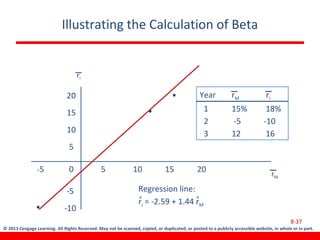
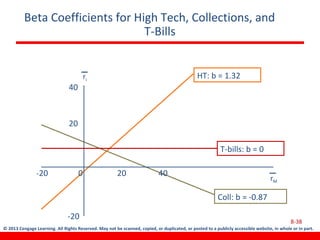
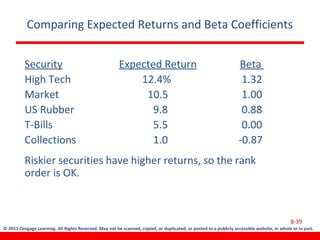
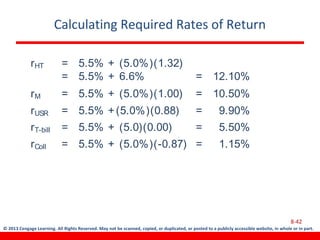
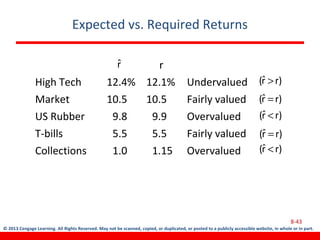
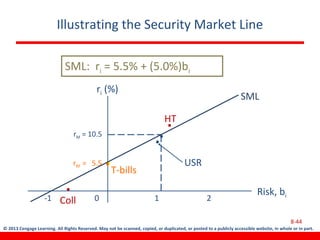
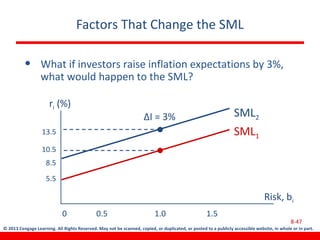
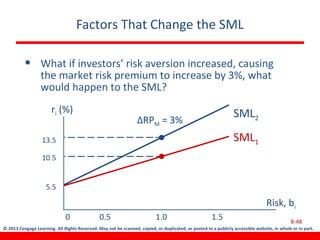
This document discusses various concepts related to investment risk and rates of return. It covers stand-alone risk, portfolio risk, standard deviation as a measure of risk, the benefits of diversification in reducing portfolio risk, and the capital asset pricing model. The key points are: 1) a portfolio's risk is generally lower than the average risk of its individual components due to diversification, especially if the components are not perfectly positively correlated; 2) standard deviation measures total risk while the coefficient of variation allows comparison of risk levels for investments with different returns; and 3) the capital asset pricing model suggests investors should only be compensated for non-diversifiable market risk, not company-specific risk.