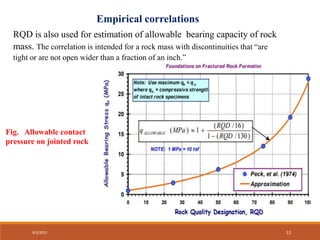
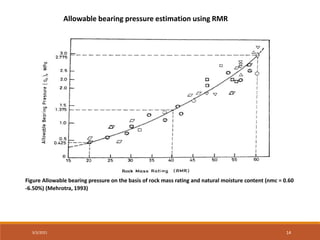
This document discusses methods for estimating the bearing capacity of rocks for foundations. It begins with definitions of ultimate and allowable bearing capacity. It then presents several equations that can be used to estimate ultimate bearing capacity based on factors like rock strength, joint spacing, and rock type. Correction factors for different foundation shapes are also provided. The document concludes by discussing approaches for determining an allowable bearing capacity value from the ultimate capacity using a factor of safety. It presents empirical correlations and guidelines from building codes for estimating allowable bearing values based on factors like rock quality designation (RQD) and rock mass rating (RMR).

1. 3/3/2021 1
Addis Ababa university
COLLEGE OF NATURAL SCIENCES
SCHOOL OF EARTH SCIENCES
Postgraduate Program(Eng. geology Stream)
Presentation

2. Bearing Capacity Estimaton of Rocks For Foundations
Outlines;
1. INTRODUCTION
2. Bearing Capacity Estimation Equations
3. Allowable Bearing Capacity Value
3/3/2021 2

3. 1. INTRODUCTION
Bearing Capacity of Rocks For Foundations.
Bearing capacity failures of structures founded on rock masses are
dependent upon joint spacing with respect to foundation width, joint
orientation, joint condition (open or closed), and rock type.
Ultimate bearing capacity
The ultimate bearing capacity is defined as the average load per unit
area required to produce failure by rupture of a supporting soil or rock
mass.
Allowable bearing capacity value
The allowable bearing capacity value is defined as the maximum
pressure that can be permitted on a foundation soil (rock mass), giving
consideration to all pertinent factors, with adequate safety against
rupture of the soil mass (rock mass) or movement of the foundation of
such magnitude that the structure is impaired.
3/3/2021 3

4. 2. Bearing Capacity Estimation Equations
A number of bearing capacity equations are reported in the literature, which
provide explicit solutions for the ultimate bearing capacity
2.1 General shear failure
The ultimate bearing capacity for the general shear mode of failure can be
estimated from the traditional Buisman-Terzaghi (Terzaghi 1943) bearing
capacity expression as follow. These equation is valid for long continuous
foundations with length to width ratios in excess of ten.
qult= cNc + 0.5γBNγ + γDNq……………………………………………………………..(2.1)
Where;
qult= the ultimate bearing capacity
γ = effective unit weight
D = depth
B = width
C = the cohesion intercepts for rock mass
Nc, Nγ and Nq are known as Terzag’ s bearing capacity factors
These are dimensionless numbers and depends upon angle of shearing resistance.
2.2. General shear failure without cohesion
qult= 0.5γBNγ + γDNq ……………………………………………..………………………..(2.22)
3/3/2021 4

5. 2.3. Local shear failure
Local shear failure represents a special case where failure surfaces start to develop but do
not propagate to the surface as illustrated in Fig.9.1a. In this respect, the depth of
embedment contributes little to the total bearing capacity stability. An expression for the
ultimate bearing capacity applicable to localized shear failure can be written as:
qult= cNc + 0.5γBN γ……………………………………..(2.3)
(2.4)
(2.5)
(2.6)
(2.7)
Cont…….
3/3/2021 5

6. 2.5 Correction factors
The above Equations are applicable to long continuous foundations with length to
width ratios (L/B) greater than ten. Table 9.1 provides correction factors for circular
and square foundations, as well as rectangular foundations with L/B ratios less than
ten. The ultimate bearing capacity is estimated from the appropriate equation by
multiplying the correction factor by the value of the corresponding bearing capacity
factor.
Table 2 Correction factors (after Sowers 1979)
Cont…….
3/3/2021 6
2.4 Compressive failure
The failure mode in this case is similar to unconfined compression failure. The
ultimate bearing capacity may be estimated from following equation.
qult=2Ctan(45+φ/2)………………………………..(2.8)

7. 2.6. Splitting failure
For widely spaced and vertically oriented discontinuities, failure generally initiates
by splitting beneath the foundation. In such cases Bishnoi (1968) suggested the
following solutions for the ultimate bearing capacity:
• For circular foundation
qult = JcNcr…………………………………………………………………………..(2.9)
• For square foundation
qult= 0.85JcNcr ………………………………………………(2.10)
• For continuous strip foundations for L/B ≤ 32
qult= JcNcr/(2.2 +0.18L/B) (2.11)…………………………….2.11
Where
• J= correction factor dependent upon thickness of the foundation rock and width
of foundation.
• L= Length of the foundation.
• Ncr = bearing capacity factor which is given by
Ncr =[2Nφ
2 / (1 + Nφ)](cot φ)(1-1/ Nφ)- Nφ(cot φ) +2 Nφ
1/2 ……………….2.12
Cont…….
3/3/2021 7

8. Fig2 Correction factor for discontinuity
spacing depth (after Bishnoi 1968)
Fig.9.3 Bearing capacity factor for with
discontinuity spacing (after Bishnoi 1968)
Cont…….
3/3/2021 8

9. A coefficient of foundation bearing capacity Nσ is used to evaluate the value of ultimate
bearing capacity. For the strip foundation shown the width is B, the axial compressive
strength and volume weight of rock foundation material is σci and , the Geological
intensity index of rock is measured by GSI, then the ultimate bearing capacity could be
demonstrated as
Where;
Qu = ultimate bearing capacity
Nσ = Bearing capacity coefficient
σci =axial compressive strength
Bearing capacity coefficient under different GSI and mi
2.7 Bearing Capacity computions using Hoek–Brown and Mohr-Coulomb
empirical failure criteria
3/3/2021 9

10. Goodman (1989) suggested, no universal formula for bearing capacity of rock can be
given. The bearing capacity can be computed from different equations that utilize the
Hoek–Brown and Mohr-Coulomb empirical failure criteria.
Kulhawy and Carter (1992) equation for calculating the ultimate bearing capacity of a
rock mass:
qult = σci (sa + (mb + s )a
where
• σci = uniaxial compressive strength of the intact rock (MPa)
• s, a = Hoek-Brown constant of the rock mass, and
• mb = Hoek-Brown constant of the rock mass rock.
3/3/2021 10

11. Goodman (1989) equation for calculating the ultimate bearing
capacity of a rock mass:
The bearing capacity for a homogeneous, discontinuous rock mass cannot be less than
the unconfined compressive strength of the rock mass around the footing. This can be
taken as a lower bound. If the rock mass has a constant angle of internal friction, φ and
unconfined compressive strength, the bearing capacity can be estimated as follows:
Qult = σci (N φ + 1)
3/3/2021 11

12. 3. Allowable Bearing Capacity Value
The allowable bearing capacity value is defined as the maximum pressure that can be
permitted on a foundation rock mass, giving consideration to all pertinent factors, with
adequate safety against rupture of the rock mass or movement of the foundation of such
magnitude that the structure is impaired.
Approaches for determining allowable bearing capacity values.
The allowable bearing capacity value, qa, based on the strength of the rock mass is defined
as the ultimate bearing capacity, qult, divided by a factor of safety (FS):
qa = qult / FS ……………………………………….(3.1)
The average stress acting on the foundation material must be equal to or less than the
allowable bearing capacity according to the following equation;
Q / BL < qa ……….……….………...........................(3.2)
Where; ‘Q’is the vertical force component of the resultant of all forces acting on the
structure, ‘B’ is the width of the footing, ‘L’ is the length of the footing and ‘qa’ is the
allowable bearing capacity value.
Building codes
Allowable bearing capacity values that consider both strength and deformation/ settlement
are prescribed in local and national building codes.
3/3/2021 12

13. Empirical correlations
RQD is also used for estimation of allowable bearing capacity of rock
mass. The correlation is intended for a rock mass with discontinuities that “are
tight or are not open wider than a fraction of an inch.”
Fig. Allowable contact
pressure on jointed rock
3/3/2021 13

14. Figure Allowable bearing pressure on the basis of rock mass rating and natural moisture content (nmc = 0.60
-6.50%) (Mehrotra, 1993)
Allowable bearing pressure estimation using RMR
3/3/2021 14

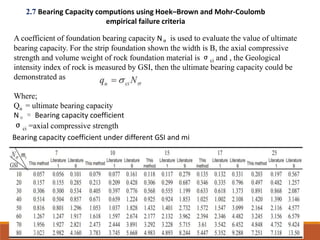
15. 3+S /B
Nj =
10 [1+300(δ/S)]
In case of rock mass with favorable discontinuities, the
net allowable bearing pressure may be estimated from:
qa = qc * Nj
Where
qc = average uniaxial compressive strength of rock cores
Nj = empirical coefficient depending on the spacing of the discontinuities
δ = thickness of discontinuity
S = spacing of discontinuities
B = width of footing
The above relationship is valid for a rock mass with spacing of continuities >
0.3 m, δ < 10 mm (15 mm if filled with soil) and B >0.3 m.
3/3/2021 15

16. Canadian practice for socketed piles and shallow foundations gives
the following simple formula for safe bearing pressure.
qa = qc * Nj * Nd
3/3/2021 16

17. Values of Kd
Depth of footing Kd
Load factor at surface 0.8
Load at radius/width of foundation unit
2.0
Load at 4 times radius/width of foundation unit
3.6
Load at 10 times radius/width of foundation unit
5.0
3/3/2021 17