This document provides a review of limit load solutions for structural components containing defects. It summarizes existing limit load solutions for plates, cylinders, spheres, pipe bends, and shell/nozzle intersections with various defect geometries under different loading conditions. The solutions are useful for failure assessment methods that utilize the limit load or reference stress concept. Experimental verification of some solutions is also discussed, along with factors such as material and geometric hardening effects.

1. Int. J. Pres. Ves. & Piping 32 (1988) 197-327
Review of Limit Loads of Structures Containing Defects
A. G . M i l l er*
Technology Planning and Research Division, CEGB Berkeley Nuclear Laboratories,
Berkeley, Gloucestershire GLI 3 9PB, UK
(Received 12 August 1987; accepted 9 September 1987)
ABSTRACT
A survey of existing limit loads of structures containing defects is given here.
This is of use in performing a two-criterion failure assessment, in evahtating
the J or C* parameters by the reference stress approximation, or in evaluating
conthmum creep damage using the reference stress. The geometries and
loadings considered are (by section number): (2) single-edge notched plates
under tension, bending and shear: (3) internal notches in plates under tension,
bending and shear; (4) double-edge notched plates under tension, bending and
shear; (5) short surface cracks in plates under tension and bending; (6)
axisynmwtric notches in round bars under tension and torsion, and chordal
cracks in round bars under torsion and bending; (7) general shell structures;
(8) surface/penetrating axial defects in cylinders under pressure; (9) surface/
penetrathlg circumferential dejects in cylinders under pressure and bending;
(10) penetrating/short surface/axisymmetric surface defects in spheres under
pressure: (11) penetrating/surface longitudinal/circumferential defects in
pipe bends under pressure or bending; (12) surface defects at cylinder-
~3'finder intersections under pressure; (13) axisymmetric surface defects at
sphere-o'linder intersections under pressure and thrust.
NOMENCLATURE
a crack depth
b ligament thickness
c constraint factor for 2D cases; crack semi-length for 3D cases
d staggered crack separation
n N/ayt
* Present address: NIl, St Peter's House, Balliol Road, Bootie L20 3LZ, UK.
197
© 1988 CEGB

2. 198 A. G. Milh'r
r notch root radius
t thickness
u b/(b + r)
x a/t in plate; meridional coordinate in cone
y 1-x
F force
Lr load/limit load for proportional loading
M plate: bending moment/length; cylinder: moment
N plate: tensile force/length
P pressure
Q mode II shear resultant
R radius of sphere or cylinder
S mode III shear resultant
:~ notch angle (0 for sharp crack, ~/2 for plain bar)
/~ semi-angle of circumferential crack in cylinder
7 2/x/3 = 1"155
q fractional ligament thickness in shell (equivalent to y in plate)
p o/(RI) 1/2
ar (G + G)/2
G ultimate tensile strength
G uniaxial yield stress
shear stress
~b meridional angle in shell
1 INTRODUCTION
1.1 Failure analysis
The two-criteria method for assessing defects ~ (called R6 from here on)
provides a method of interpolating between plastic collapse and fracture
governed by linear elastic fracture mechanics. An accurate assessment of
plastic collapse would take into account material hardening, finite strain and
finite deformation effects. Commonly, however, a simpler assessment is
performed using limit analysis, and neglecting these effects. This note gives a
list of available limit analysis solutions for c o m m o n structural geometries.
Limit analysis may also be used for assessing other fracture parameters.
The elastic-plastic parameter J may be assessed by reference stress methods
using the limit load. 2"3 The creep crack growth parameter C* may be
estimated by assuming that the creep stress distribution is similar to the
stress distribution at the limit load.* The reference stress itself is used to
assess continuum damage due to creep. 5

3. Review of limit loads of structures containing defects 199
1.2 Limit analysis
Limit analysis calculates the maximum load that a given structure made of
perfectly plastic material can sustain. The loading is assumed to vary
proportionally with a single factor. The maximum sustainable load is called
the limit load, and when this load is reached the deformations become
unbounded and the structure becomes a mechanism.
The effect of large deformations is not considered in the solutions given
here (except in the case of axial thrust on nozzles in spheres).
Complete solutions are hard to calculate, but bounds may be obtained by
using the two bounding theorems. A lower bound to the limit load is
obtained by a statically admissible stress field satisfying equilibrium and
yield, and an upper bound is obtained by a kinematically admissible strain
rate field satisfying compatibility and the flow rule. Usually a safe estimate
of the load-carrying capacity of a structure is required, and a lower bound is
appropriate. Sometimes, however, R6 is used in an inverse manner to assess
the maximum defect size that would have survived a proof test. Then an
upper bound may be appropriate.
1.3 Geometries considered
Most of the solutions given here are effectively two-dimensional, being
derived from plane strain, plane stress or thin shell assumptions. As far as
possible a uniform notation has been maintained, but the notation has been
repeated for each geometry to avoid confusion. The limit loads have been
made non-dimensional by referring them to the limit load of the unflawed
structure, or to the load given by a uniform stress across the ligament.
The different geometries are considered in order of increasing structural
complexity; that is, plates, cylinders, spheres, pipe-bends, shell/nozzle
intersection. Within each of these geometries different defect geometries are
considered. Where possible, an analytical representation of the results is
given. Where this is not possible, the results are presented graphically for a
range of geometries.
1.4 Experimental verification
Where available a comparison is given between theory and experiment. Care
must be taken that the experiments are indeed governed by plastic collapse.
For small testpieces made from aluminium or mild steel, however, brittle
fracture is demonstrably unimportant if

4. 200 A. G. Miller
where K: is the appropriate critical stress intensity factor, ~y is the yield stress
and a is a characteristic length such as defect size or ligament size. If ligament
fracture or m a x i m u m load is used, then the flow stress should be used to
normalize the result (see Section 1.5). Alternatively, deformation-based
criteria can be used, and in this case the yield stress should be used as
normalization. The deformation (or strain) definition given by A S M E 6 is as
follows:
NB-3213.25 Plastic Analysis-Collapse Load. A plastic analysis may be
used to determine the collapse load for a given combination of loads on a
given structure. The following criterion for determination of the collapse
load shall be used. A load-deflection or load-strain curve is plotted with
load as the ordinate and deflection or strain as the abscissa. The angle that
the linear part of the load-deflection or load-strain curve makes with the
ordinate is called 0. A second straight line, hereafter called the collapse limit
line, is drawn through the origin so that it makes an angle q~= t a n - t(2 tan 0)
with the ordinate. The collapse load is the load at the intersection of the
load-deflection or load-strain curve and the collapse limit line. If this
m e t h o d is used, particular care should be given to ensure that the strains or
deflections that are used are indicative of the load-carrying capacity of the
structure.
Depending on the choice of deformation/strain c o m p o n e n t and location,
the value of the collapse load will vary. Gerdeen v recommended using the
generalized displacement conjugate to the load in order to remove this
ambiguity.
1.5 Material and geometric hardening
Limit analysis ignores the hardening of the material, and so a choice must be
made as to what value of stress to use in the limit solution. To evaluate the L r
parameter for R6 Rev. 3 the 0"2% p r o o f stress t~y should be used. The cut-off
at L~ ax is based on the flow stress (ay + o,)/2, except where higher values may
be justified. For the assessment of C - M n steels given in Appendix 8 of R6
Rev. 3, the S, parameter is evaluated using the flow stress (oy + au)/2 again.
Geometry changes lead to both hardening and softening, for example:
(1) plates under lateral pressure become stiffer as membrane effects arise;
(2) tension produces thinning which may lead to instability;
(3) compression gives rise to buckling (limit point or bifurcation);
(4) meridian line changes in pressurized nozzles increase stability.
1.6 Approximate solutions
For structures where there is no existing limit solution, the solution may be
calculated, using one of the bounding theorems, or determined experi-

5. Rev&w of limit loads of structures containing defects 201
mentally. A c o m m o n way of calculating a lower bound solution for a shell is
to calculate the stresses that would be present if the structure were uncracked
and elastic (which is always possible using finite elements) and then to take
the elastic value of the stress resultants across the cracked section and use the
appropriate limit load expression for a plate in plane stress or strain under
combined tension and bending.
The Tresca plane stress limit solutions depend only on the plane of the
ligament. In perfect plasticity it is permissible to have local discontinuities in
the other components of the stress resultants, and hence their elastic values
may be ignored. If desired, they may be specifically taken into account by the
method in Section 2.12.
In plane stress with the Mises yield criterion, or in plane strain with either
the Tresca or Mises yield criterion, the stress field caused by the defect
extends a distance of order t from the defect. If this is small compared with
the characteristic shell distance (Rt) t/2, then the higher plane strain limit
solution may be more appropriate than the plane stress limit solution. The
Tresca plane stress solution relies on the ligament plane being free to neck
down. If it is constrained from doing this, say by shell curvature, then it will
be in plane strain. R6 Rev. 3 recommends the plane stress solutions in
general.
A less conservative estimate is given for short cracks by taking the stresses
calculated elastically for the cracked body. This is discussed further in
Section 1.8.
1.7 Multiple loading
If it were desired to combine the solutions here with other types of loading
for the same geometry, a conservative estimate may be derived from the
convexity lemma (see, for example, Ref. 8). Consider a set of independent
load parameters p~. Then proportional loading is defined by
Pi = /'PiO
where 2 is a variable andpio is constant in any particular case. There will be a
unique value of 2 = 2 o at which equilibrated plastic flow takes place. There
will be such a value 2 corresponding to every set of ratios pi o. Hence 2o,pi o
defines a yield point loading surface in the multi-dimensional load space.
The convexity lemma states that this yield point loading surface is convex, as
a consequence of the convexity of the yield surface. Hence the planes
through the intersections of the yield point loading surface with the axes
form an inscribed surface, and a lower bound to the limit load is given by the
criterion
Piy
i

6. 202 A. G. Miller
where Ply are the limit loads under a single type of load. The displacement
boundary conditions must be the same in each case. For example, results are
given here for the limit loads of plates under combined tension and bending.
However, if the limiting values of the stress resultants under pure tension
(and zero moment) and pure bending (and zero tension) are given by
INI ~< No and IM[ ~< Mo
respectively, then a lower bound to the limit load under combined tension
and bending is given by
INI + [MJ
N--~ M o <~1
1.8 Global and local collapse loads
Conventional limit analysis calculates what may be called the 'global'
collapse load, at which displacements become unbounded. However, in
elastic-plastic structures, the plastic strains at the ligament may become
large long before the global limit is reached, and hence an estimate of the
'local collapse load' at which gross plasticity occurs in the ligament may be
more relevant to ligament fracture.
In the case of through cracks, there is obviously no ligament to yield
before general yield, but it is conceivable that there may be a local instability.
Miller 9 considered surface defects in tension in plates and steels (see Fig. 1)
and concluded that ductile failure occurred at a nominal strain of
kt-at
E--
4 a c
where k is a material constant between 0.4 and 1-5 for the mild steels
considered. If e is greater than the material strain at the flow stress, then the
cut-offat L maxis described by the structure limit load. Ire is less, then the cut-
offshould be taken at a load based on a reduced flow stress. Ire is less than
the yield strain, then the local collapse load should be used with the flow
stress.
Q
2c
Fig. 1. Geometry of surface defect.

7. Review of limit loads of structures containing defects 203
2h
.[
0 0 0 0
@ ® @ @
T
Fig. 2. Geometry of embedded defect.
Ewing '° considered an eccentric defect in mode III (Fig. 2) and
constructed the failure assessment line using a critical crack tip opening
displacement criterion. He concluded that this agreed well with the R6
diagram using the global collapse load, although there was a small dip inside
the diagram at the local collapse load. Bradford tt derived a simplified
plastic line spring model to calculate J for surface defects. Only one
numerical example is given, and in this the global collapse load gives a better
reference stress than does the local collapse load.
Miller t2 reviewed published calculations of J at surface defects for plates
in tension, cylinders with circumferential defects in tension and cylinders
with axial defects under pressure. In all cases the global collapse load gave
better reference stress J estimates than did the local collapse load but the
number of results was small.
R6 recommends the use of the local collapse load, as it is conservative.
There are a large number of test results for L~ ax which show that this
conservatism may be relaxed at ductile instability, but the evidence in the
elasto-plastic r~gime is still limited.
This issue may be resolved by performing a J-integral calculation (as in R6
Rev. 3). The ligament behaviour should be controlled by J. If this is
estimated by the reference stress method, the appropriate limit load to use
remains to be resolved.
1.9 Defect characterization
The existing codes, which give rules for defect characterization (Refs 13, 14
and R6), give rules which are based on LEFM. At present there is little

8. 204 A. G. Miller
information about how defects should be characterized for the purpose of
assessing plastic collapse. However, it can be stated that if the defect size is
increased, the plastic collapse load cannot be increased, so circumscribing a
defect with a bigger effective defect is always conservative.
Miller t5 considered ductile failure test results for a variety of multiple
defect geometries and concluded that the code characterization was always
conservative. For purely ductile failure, net section area was a valid method
to use, and thin or multiple ligaments did not need any special treatment
except for that described in Section 1.8.
The limit solutions available in the literature for notched plates consider
the geometries with a finite root radius, or a V-shaped notch with any given
flank angle. The stress intensity factor is only relevant for sharp, parallel-
sided notches, and in practice defects are characterized for assessment
purposes as being of this form.
1.10 Yield criteria
The most c o m m o n l y used yield criteria are Tresca and von Mises:
Tresca max {]0.2 - 0.3], ]0.3 - atl, 10.1- 0._,1}= %
2
Mises (0.~ + 0. 5 ...[_0.2) __ (0.20.3 + 0"30"1 -'{'-0"10.2) m 0.:,,
or (0.~1+ a~z + a~3) -{022033 + 0.330"11 "~-0.110"22) + 3(0.-~3+ air + 0.~2) = Cry
0.~ principal stresses 0"~j stress components ay uniaxial yield stress
It can be shown that the difference in limit load given by these yield surfaces
is
N/3 3
0"866L~t" = 2 L~I, <~ Lr~< L,~I. ~ < 5 5 L T = l ' 1 5 5 L T
where L r and Lxl are the Tresca and Mises limit load respectively. In practice
this difference is small compared to other factors, and the choice is usually
made on grounds o f convenience.
1.11 Yield criteria for plane stress and plane strain
The yield criteria for plane stress (a 3 = 0) and plane strain (% = 0) are shown
in Fig. 3.
For plane stress the yield surfaces are plotted by putting 0.3 = 0 in the
above yield surfaces, to give a hexagon (Tresca) or an ellipse (Mises) as in
Fig. 3. For plane strain the condition % = 0 implies that
(0.1 + 0.'2)
0"3-- 2

9. Rerie,' ~I" limit loads o/'structures containing defects 205
PLone stroin
/
//
C[2,,. / Plane ~ ( ' ~ e'e
~" ,/Mises stress , ~,e~
, I: /,/¢"
, 2 "
IJ/,,"
"
t /
f#
Fig. 3. Plane stress and strain yield criteria.
and consequently Je~ - 02] is constant. It equals ay for Tresca and 1"155cr, for
Mises. The yield surface is thus two parallel lines as in Fig. 3.
As the plane strain yield surface circumscribes the plane stress yield
surface for both Tresca and Mises, the plane strain limit load is always
higher. Moreover, as the Mises plane strain surface may be obtained by
scaling the Tresca plane strain surface by a factor of 2/x/3, the limit loads are
in the same ratio. This increase in limit load is described by the constraint
factor c:
L
Tresca plane strain c=
LTo
L
Mises plane stress c=
/-'To
Mises plane strain c=
,/3L
2LT~
where L is the appropriate limit load and LT~,is the Tresca plane stress limit
load. Hence the two plane strain constraint factors are the same but the
plane strain Mises limit load is 1-155 times the plane strain Tresca load. It can
be seen from Fig. 3 that
1 ~< c ~ 1.155 Mises plane stress
whereas in plane strain the constraint factor is unbounded. The constraint
factor may also be regarded in tensile cases without bending as the ratio of
the average stress to the yield stress (or 1-155ay for plane strain Mises).

10. 206 A. G. Miller
1.12 Yield criteria for shells
Shell calculations are done using the tensile and bending stress resultants
rather than stresses. As the relationship between the yield criteria for stress
resultants and those for stresses are complicated, simplified yield criteria are
commonly used for shell stress resultants. The shell is in a state of plane
stress, and the commonest criterion is the two-moment limited interaction
yield surface shown in Fig. 4. Hodge 8 shows that
0"618LL ~<LT ~<LL 0"618Lt. ~< L,4 ~< I'155LL
where L:4 = Mises limit load, LT = Tresca limit load and t L = two-moment
limited interaction limit load.
-1
I
m2 1
i !
Fig. 4. Two-momentlimited interaction yield surface for shells.
However, as the bending and stretching are rarely significant simul-
taneously, the approximation is often better than implied by the inequalities.
However, the limits may be achieved in simple loading cases when both
bending and stretching are important. The origin of this factor 0"618 may be
illustrated by considering the case of a plain beam. The results in Section
2.4.1 show that for Tresca plane stress
( ~ r t ) 2 + 4a-~-2=1
When
N 4M
~yl~Gyl 2
this gives
N 4M x/5_- 1_0.618
ay--~=cryt2 = 2

11. Review of limit loads of structures containing defects 207
Using the limited interaction yield surface gives
N 4M
o-rt o-yt2 -
If this yield surface is used without the 0"618 factor being applied, the
absence of simultaneous bending and stretching should always be checked
for. The collapse of a shell under boss loading (point force) provides a
counter example in which bending and stretching arise simultaneously (in
the h o o p direction). This is shown by Ewing's results discussed in Section
13.2.
For thin shells in a m e m b r a n e stress state the Mises and Tresca yield
criteria give the same result for equibiaxial stresses, as in a pressurized
sphere:
P = 2ayt both Tresca and Mises
R
When the two principal stresses are not equal, Mises gives a higher limit
load, the difference being at its m a x i m u m when the stress components are in
a ratio of 2:1, as in a closed pressurized cylinder:
P = tryt
R Tresca P = ~2tryt Mises
If the two principal stresses are of opposite sign, then the Mises/Tresca
ratio reaches 2/,,/3 at (1, - 1,0) and is between 1 and 1-155 for other values.
2 S I N G L E - E D G E N O T C H E D PLATES
These have been extensively studied. Most work has been done on the plane
stress and plane strain cases rather than finite crack lengths. This is of more
relevance to test specimen geometries than to structures. The plane strain
case can be analysed by slip-line field theory which gives an upper b o u n d
when the solution is not complete. 'Complete' means that a statically
admissible stress field has been extended into the rigid regions adjacent to
the plastic regions. Sharp cracks are considered first. A review of limit loads
for these is given by Haigh and Richards, ~6 and a review of test results is
given by Willoughby} 7 The effect of notch root radius and flank angle is also
considered. These can only reduce the limit load, as material is being
removed compared to the sharp crack geometry.
For elastic material with a .V notch, the power of the stress singularity
alters, and with a rounded root the stress singularity becomes a finite stress
concentration. Hence in neither case is the conventional stress intensity

12. 208 A. G. Miller
factor, strictly speaking, a valid parameter. In practice defects are usually
assessed pessimistically assuming them to be sharp:
a defect length M moment/width
b ligament thickness N force/width
r root radius Q mode II shear force/width
t thickness S mode III shear force/width
u b/(b+r) ay yield stress
x a/t ~t notch angle
y 1-x
The geometry is shown in Fig. 5.
QS
Q
u
N
IM M':M+I/2 Na
i
a
t t
a
y:_l - a~- : I - ~
~. ligament
I
plate
I I N Tension
I i M Bending moment
I I Q Mode TT shear
S Mode TIT shear
---N ~
-- Q
X S
_ ¢1
Fig. 5. SEN geometry.

13. Review of limit loads of structures containing defects 209
2.1 S E N B pure bending ( N = 0)
2.1.1 Plane stress Tresca
4M(x_____~) (1 - x) 2 = y2
= 0 ~< X ~< 1
O'yt 2
2.1.2 Plane stress Mises ~8
Deep cracks
4 M ( x ) _ 1.072(1 - x) z = 1-072y z x > 0.154
O'yt 2
T h i s result is o n l y valid f o r d e e p c r a c k s a n d m u s t be c o n t i n u o u s with the
u n n o t c h e d b e a m result:
4M(0)
- - = 1
O-yt 2
T h e value o f the validity limit o n x is t a k e n f r o m O k a m u r a et al. 19
2.1.3 Plane strain Tresca
D e e p c r a c k s 2°
4M
= 1"2606(1 - x ) 2 1'2606v 2 x > 0"295
~yt 2
Shallow c r a c k s 2
4 M ( x ) = [ 1.261 - 2"72(0"31 - x)2](l - x) z x < 0"295
o'rt 2
= [1 + 1"686x - 2"72x2](1 - x) z
1 - 0"31x x--*0
T h i s is an a n a l y t i c a p p r o x i m a t i o n to within 0"5% to the values given in
T a b l e 1. T h e results are s h o w n g r a p h i c a l l y in Fig. 6.
2.1.4 Plane strain Mises
T h i s is 1"155 times the p l a n e strain T r e s c a result.
2.2 S E N T tension ( M = 0, pin loading)
2.2.1 Plane stress Tresca 22
N
- n(x) = I-(1 - x) 2 + x23 ~/2 - x 0~<x~<l
tTyt
= [1 - 2x + 2 x 2 ] 1/2 - X
n ~ 1 - 2x x~0
y2
n ....~ _ _ y-,0
2

14. c: Z,N ( Tresco )
% (t-al 2
1.3
1.2
1.1
1.0 [ I I
o .1 .2 .3 o / t
Fig. 6. Constraint factor for SEN plate in bending in plane strain.
TABLE !
Limit Moment Plane Strain for Single-edge Notched Plate
(from Ewing 21)
a/t = x c (1 - - x ) ' c a/t = x c (I --x)2c
0"296 1'261 0'625 0"089 1'125 0.934
0'258 1"255 0-691 0"065 1.095 0-956
0.249 1.244 0'739 0"060 1.090 0.963
0'197 1"226 0-791 0'036 1-056 0.981
0.164 1'200 0"839 0"017 1.028 0'993
0-130 1' 169 0"885 0.004 I '008 1'000
0"096 1'133 0'926 0 1 1
x = a / t fractional crack depth.
c = constraint factor:
4M 4M
ayt2(l_x)2 (Tresca) 1.155a/Z(l_x)2 (Mises)

15. Review of limit loads of structures containing defects 211
This is the same as in the plain b e a m result f o r c o m b i n e d tension a n d
bending, with the m o m e n t given by the eccentric tensile force o n the
ligament:
Na
M=
2
2.2.2 Plane stress Mises 22"z3
Deep cracks
N_N_=n(x)=[-[ " )'-- 1'~ 2 _ x ) Z ] l/z f 7--1'~
.., Lt-.+--r-) +7(1 - t?x--~--) x >0"146
= --7(l+y)x+v(l+v)x 2 -- 7x--
7y 2 2
for y - ~ O n~ 1 +7=0.536y2 7 - - - ~ r ~ = 1.155
I f 7 is put equal to unity, the Tresca result is recovered.
Shallow cracks
N
= n(x) = 1 -- x -- x 2 x < 0"146
o'rt
T h i s is an a p p r o x i m a t i o n to the t a b u l a t e d results in E w i n g and
R i c h a r d s 2z'za agreeing to within 0-15%:
n-+l -x x--*0
2.2.3 Plane stra& Tresca
D e e p cracks 22'z3
N
- - = n = 1-702{ I-(0-794 - 392 + 0"58763 ,2] 1/2 - [-0-794 - y]} x > 0.545
O'yl
n ~ 0"6303 '2 y~0
Shallow c r a c k s z4
N
-- n(x) x < 0.545
• o'yt
where
n(x)/> 1 -- x - 1.232x 2 + x 3 - f ( x )
and
n(x) ~ f ( x ) + 22x3(0.545 - x) 2
n ----~ 1 - - x x~0

16. 212 A. G. Miller
The pin-loaded limit forces are shown graphically in Fig. 7. This also
shows the results of plane stress tests on mild steel specimens by Ewing and
Richards.22"23
2.2.4 Plane strain Mises
This is 1"155 times the Tresca plane strain result.
2.2.5
K u m a r et aL 25 give values for the limit loads which are the Tresca plane
stress results renormalized to give the correct result as x ---, 1. They are not the
correct limit load and are not recommended for use. The variation of their
h(n,x) functions with n would be reduced if they were normalized with
respect to the correct limit load as a function of x. (If reference stress theory
were exact, the variation would vanish.)
2.3 SEN tension with restrained rotation (fixed grip)
2.3.1 Plane stress Tresca and Mises, and plane strain Tresca
N
~yt
For Tresca plane stress this result may be derived by putting M = -½Na
into the expressions given in Section 2.4. The negative moment, shallow
crack combined bending and tension solution is not available for the other
cases, however.
This is compared with the pin-loading results in Fig. 7.
Z0
i
1.0 ',~ ---Io It U--19- o l -
I. l J
P Tresca plane strain ] Pin-
0.8
~"~,C,,._ M Mises 1 -. ~ loading
N e~'" T Tresco t wtane|
O'yt 06
~ Ist~ess/
~'~ ~" ~,F • Experimental J )
~',,~ "% ~ . _F_ PLanest.,s~ onO rres=o plan*
0/*
0.2
0 I l I L, I l l F ~ "~"'~I
0.1 0.2 03 0.~, O.S 06 0.7 08 0.9 I0
alt
Fig. 7, The theoretical and experimental variation of yield load with notch length for single-
.
edge notched (SEN) specimens (from Ewing and Richards ....~3 ).
~

17. Review o[ limit loads of structures containing defects 213
2.3.2 Platte strain M i s e s
This is 1"155 times the Tresca plane strain limit load.
2.4 SEN combined tension and bending
This case may be derived from a transformation of the pin-loaded results, by
a method suggested by Ewing. 22"23 Equivalent results are given by Rice 26
and Shiratori and Dodd. 2~ Proportional loading is assumed. The results are
only valid for deep cracks. The signs are positive for forces and m o m e n t that
tend to open the crack. The effect of crack closure has been ignored:
applied load
Lr = limit load (in R6 Rev. 3 notation with limit load based on or)
( t -- a) N
3'~ - 2 M + N t (for M = 0, y, = 3')
(2M + Nt)q(y~) ),2 N
Lr = crr(t -- a) z q(Y~) n(y~) n(.v) = --tryt
where n is the appropriate function (Tresca or Mises plane stress or plane
strain) taken from Section 2.2 for the pin-loaded case and ),e is the effective
fractional ligament thickness as defined above.
It follows from this that in all cases the results in Section 2.1 obey
4M
°'rt 2 * 2nO') as ) , ~ 0
That is, the tensile force for very deep cracks is governed by the m o m e n t due
to the eccentricity of the ligament.
These results may be rewritten in terms of the m o m e n t referred to the
centre-line of the ligament:
M' = M + Na/2 L~ LGr(t _ a) 2 a,(t- a) q(Y~)
N/( t -- a)
)'e = ( 2 M ' ) / [ ( t - a) 2] + N / ( t - a)
This shows that only the stresses referred to the ligament affect the limit load.
The thickness t has no effect, provided that the crack is sufficiently deep. The
criterion for sufficient depth will now depend on the ratio N / M , and this
must be considered separately for each case. For Tresca plane stress the deep
crack solution is always valid. For Mises plane stress the shallow crack
solution is unknown. For Tresca or Mises plane strain the shallow crack
solution is discussed in Section 2.4.5.

18. 214 A. G. M i l l e r
2.4.1 Plane stress Tresca
The results m a y be written
2 M + Na + [(2M + Na) 2 + N2(t - a) 2] t2
Lr = O'y(t -- a) 2 0< x < 1
This is identical to eqn A2.4.4 in R6 Rev. 2. It is identical to the u n n o t c h e d
b e a m result:
V + - ? - =1
with a c c o u n t being taken o f the effect o f ligament eccentricity:
M---, M + Na/2
As the square root m a y have either sign, and plastic collapse m a y occur in
either tension or compression, the expression for L r m a y be rewritten
I2M + Na[ + E(2M + Na) " + NZ(t - a) z] 1/2
t r=
a~(t -- a) z
where now the positive square root sign is always taken.
2.4.2 Plane stress M i s e s
The a n a l o g o u s results apply. The deep crack validity limits are given by
O k a m u r a et al. 19
O.1540{l+N/[ay(t-a)]} if N
x> xo = - - <0"5475
1 + O'1540{N/[ay(t - a)]} ay(t - a)
N
x > x o < 0-220 if - - > 0"5475
o'y(t - a)
M !
cry (t -o )z .--.'_--_" Upper bound
Ewing a n d Richords
1.2-
" Lower b o u n d
Okomuro etal.
- ~"~."~=~'~ / o/t = 0 22
" V. ol t = 0.1
N~g.. o/t = 055
~N~. a / t = 0.0
%
V I I I 1 I I 1 I 1 I i I 1 t I I i I~ I
-lO -0.5 0.5 1.0
M= = M q.1/2No
Fig. 8. Limit moment and force for SEN plate (from Okamura et al. 1 9 ). Plane stress Mises.

19. Review of limit loads of structures containing defects 215
This depth limit agrees with the value OfXo = 0-154 for pure bending given in
Section 2.1.2 at the validity limit:
N N
x=0-146 ~ = 0-832 - - = 0.974 > 0.5476
ayt ar( t -- a)
This therefore satisfies x 0 = 0.146 < 0-220 and is consistent with the above.
O k a m u r a derived lower bounds for shallow cracks. These are shown in
Fig. 8.
2.4.3 Plane stra& T r e s c a 24
The analogous results may be rewritten for deep cracks (where 'deep' will
be defined later) in terms of x = a/t:
~deep' cracks (in terms of Ye), i.e. bending-dominated
q(ye) = 0.794 - .re + [-(0.794 - 3,)2 + 0.588y2] 1/2 y, < 0"455
"shallow' cracks (in terms of yo), i.e. tension-dominated
q(y~) ~< v~ > 0"455
y~ -- (re + 0"232)(1 -- ye) 2 "
q(Y~) > y2
Ye -- 0', + 0"232)(1 --y,)2 + 22(1 - - ) ' e ) 3 ( y e -- 0"455) 2
These expressions are shown in Fig. 9.
The crack depth limit is given by
N 6M
x>0-4 x>0 M=0 x>0-295 N=0
l 12
The transitional value of 0"4 is the m a x i m u m for all values o f M / N t (i.e. the
deep crack solution is valid for all M / N t if x > 0.4).
Ewing's expressions were developed for the positive tension, positive
bending quadrant. The solution for all sign combinations is shown in Fig. 10
for deep cracks.
An alternative representation of the bending-dominated r6gime is given
by Shiratori and Miyoshi: 29
m " = 1-26 + 0.521 n" - 0-739(n") 2 0 ~< n" ~ 0"551
where
4M' N
a,(t - a) 2 a,(l - a)

20. 1.tl
2 M . Nt
1.6
L r = (t-o) 2 cry q(Y)
1.4
1.2
q(y)
1.0
Upper bound /
0.~,
Lower bound
06 to q
I I l I
02 0t. 06 08
y: (t-o)/ (t.2MIN)
Fig. 9. Limit moment and force for SEN plate (from EwingZ'~). Plane strain.
..... Rice's upper bound
..... S h i r o t o r i a n d Dodd field
Rice opproximote
expression
,.,
1.0
O.S m " -= 4 M'
/
, 0.6 o-y (t_o)Z
/ ,,/ O.Z. . . . . / . n ~* =
- N
/ O.Z Cry ( t - o )
/
-~.l-o.s -o.~'-o.'4--o'..Zo2 o z o.~ o.~ o.a/o n"
,,/
i,~ -0.6
-0.II ""
'.~ -"
Fig. i0. Combined bending and tension for deep-cracked SEN plate in plane strain (from
Nicholson and Paris~S).

21. Review o f limit loads o f structures containing defects 217
TABLE 2
SEN Plane Strain Upper Bound for Shallow Cracks
(from Ewing 24)
N
Values of ~ (Tresca) or - - (Mises)
o'yt 1-155oyt
6M/Nt
a/t 0.5 1 2 4 8
0'05 0"826 0-702 0'520
0-10 0-794 0-672 0.495 0"307 0-167
0"15 0-752 0"633 0.463
0"20 NA 0"584 0-424 0"260 0.141
0"25 0.527 0"379
0"30 0"464 0-330 0'200 0"109
0-35 0-396 0"279 NA NA
NA: not applicable.
2.4.4 P l a n e s t r a i n M i s e s
This is 1"155 times the plane strain Tresca limit load.
2.4.5 S h a l l o w c r a c k s in p l a n e s t r a i n ( T r e s c a or M i s e s ) t9"24"28"3°
T h e results are no longer expressible in terms o f a single f u n c t i o n q(Ye) only,
as for d e e p cracks. Physically the r e a s o n is that plastic yielding can spread to
the top free surfaces on either side o f the notch. Ewing derived an u p p e r
b o u n d solution f r o m the shallow c r a c k b e n d i n g solution. His results are
given in Tables 2 and 3.
T a b l e 2 gives an u p p e r b o u n d limit load for the region w h e r e the shallow
crack solution is a p p r o p r i a t e . T a b l e 3 c o m p a r e s these results with the p u r e
b e n d i n g results for shallow cracks given above, and the values t a k e n f r o m
TABLE 3
SEN Plane Strain Upper Bound for Shallow Cracks
4M
Values of 4M (Tresca) or (Mises)
~yt2 I-I 55ayt2
a/t a b a/t a b alt a b
O"10 0'89 0"92 0"20 0"75 0-79 0.30 0-58 0-62
a Taken from Table 2 with 6M/Nt = 8.
b Taken from Table I with 6M/Nt = zc.

22. 218 A. G. Miller
Table 2 are slightly lower than the values taken from Table 1, as they should
be.
2.5 SEN approximate solutions for combined tension and bending
2.5.1
R6 Rev. 2, eqn A2.4.5, gives an empirically modified version of the Tresca
plane stress result:
II'5M + Nal + [-(l'5M + Na) 2 + N2(t - - a ) 2 ] 1/2
Lr = o'y(t - - a ) 2
This expression is no longer recommended. It is 6% non-conservative
under pure bending compared to Tresca plane strain but conservative under
combined tension/bending.
2.5.2
The classical plate formulae are pessimistic because they assume that the
ends are free. An approximation sometimes made, 3t'32 or in O R A C L E by
Parsons, 33 is to ignore the contribution to the bending moment produced by
the eccentricity of the tensile force:
Met f = M -- ½Na
This cannot be rigorously justified, and it should be confirmed that
redistributing the moment ½Na does not cause another part of the structure
to be in a more onerous condition than the ligament. This version is used by
O R A C L E for both the Tresca plane stress formula and with the R6 Rev. 2
modification of this.
BS PD6493 uses the Tresca plane stress version of this approximation.
2.5.3
Chel132 gives an approximate solution for plane strain which is equivalent to
the solution here for deep cracks, and is based on a conservative
approximation to the pin-loading SENT results when a/t < 0"545.
2.6 SENB pure bending: effect of notch angle
2.6.1 Plane stress Tresca
The constraint factor is unity, independent of notch angle 2:~:
4M
O.rt2(1 __ X) 2 = 1
C -------

23. Review of limit loads of structures containing defects 219
~
I 1.07
1.06 Upper bound
Lower bound
~.os
a
"- I .Or,
~" 1.03
o
'- 1.02
E
0 1.01
U
1.00 , , , A /,lO /
0 i ~ I
90 80 70 60 5 0 3 20 10 0
Fig. 11. SENB with V-notch: plane stress Mises (from Ford and Lianists).
2.6.2 P l a n e stress M i s e s t s
For deep cracks
4M
C = crrt2( 1 _ x) 2
4/(,,/3)
0 < ~ < 67 ° c = 1 + 2/(,,/3) = 1.072 (exact)
67 ° < :~ < 75 ° c = 1"173 - 0"0859~ :~ in r a d i a n s
75 ° < :~ < 90 ° c = 1 + 0"229(rc/2 - :~) ~ in r a d i a n s
F o r :~> 67 ° b o t h l o w e r a n d u p p e r b o u n d s are given, a n d t h e y are b o t h
r e p r e s e n t e d b y the a b o v e f o r m u l a e to w i t h i n 0"5%.
T h i s is c o n t i n u o u s with the d e e p s h a r p n o t c h result f o r ~ = 0 (c = 1.072)
a n d the u n n o t c h e d b a r f o r ~ = re/2 (c = 1). T h e d e p t h v a l i d i t y limits are n o t
k n o w n , e x c e p t f o r :~ = 0 a n d ~ = ~/2.
T h e results are s h o w n in Fig. 11.
2.6.3 Plane strahl Tresca 2°'34
4M
c = aytZ(l _ ..)2
0 < :~ < 3"2 ° c = 1"2606 (exact)
3.2 ° < :~ < 57"3 ° c = 1"2606 - 0 " 0 3 8 6 :~" - - -"°~° ~ 6"J
( 0-944 ^ ' ~
'^ :~ in r a d i a n s
T h i s f o r m u l a r e p r e s e n t s E w i n g ' s n u m e r i c a l results to w i t h i n 0 " 3 % :
rc - 2:(
57"3 ° < ~ < 90 ° c= 1 + (exact) :~ in r a d i a n s
4+rc-2~

24. 220 A. G. Miller
I.I.
~1,3
u
O
C
e,
o
1.1
1
9O ;o 4 6% ;o ,'0,'o 21, ,'o
oK
Fig. 12. SENB with V-notch: plane strain [from Green'°).
T h e d e p t h r e q u i r e m e n t s are: 3"*
1
0<:~<57.3 ~' - - > 1 . 4 2 3 - 0 . 1 2 4 : ~ 2 :t in r a d i a n s
1-.
1 e ~2-~ -- 1
57-3 ° < ~ < 90 ~ ~ > l -~ ~ in r a d i a n s
1 -x 2 + ~z/2 -
T h i s is slightly m o r e stringent t h a n G r e e n ' s d e p t h r e q u i r e m e n t s .
T h e s h a l l o w c r a c k s o l u t i o n is not k n o w n . T h e s o l u t i o n here is c o n t i n u o u s
with the d e e p c r a c k s o l u t i o n at :~ = 0 (c = 1.2606) a n d with the u n n o t c h e d b a r
s o l u t i o n at :t = re/2 ( c = 1). T h e results are s h o w n in Fig. 12.
Dietrich a n d Szczepinski 35 give the c o m p l e t e slipline field for :t = 60: a n d
their c o n s t r a i n t f a c t o r is the s a m e as a b o v e .
2.6.4 Plane strain Mises
T h i s is 1"155 times the plain strain T r e s c a limit load.
2.7 P u r e b e n d i n g : effect of notch root radius
2.7.1 Phme stress Tresca
4M
= 1 ahvays
t? -- O.y12 ( 1 -- .V) 2
2.7.2 Phme stress Mises Is
n o t c h r o o t radius r
ligament b = t - 2a
b+r
4M
C = ayt2 (1 -- X) 2

25. Reciew o f limit loads o/" structures containing defects 221
1.061.07 J
t Upper b o u n d
I. 05 Lower bound... /j/
u
0 1.0¢
"c 1.03
'6 1.oz
ut 1.01
g
U 1.00 / I .I I I I I I 1.10
0.1 0 . 2 0 3 0/, 0 5 0 . 6 0 . 7 0 . 8 0 9
b
b+r
Fig. 13. S E N B with circular root: plane stress Mises (from Ford a n d LianistS).
For deep notches
0 < u < 0"692 c = 1 + 0"045u 2 to 0.2%
0.692 < u < 1 c = 1.072 0"123r
+ 0"022 ( r ) 2
~ to 0"6%
Both lower and upper bounds are given, and are represented by these
formulae to the stated accuracy.
This merges continuously with the deep sharp notch solution at r = 0
(u = l, c = 1"072) and the unnotched bar solution at r = ~ (u = 0). The depth
limits are not known, except for u - - 0 and u = 1. The results are shown in
Fig. 13.
2.7.3 Plane strain Tresca 2°
4M
c-ayt2(1-x)2
Deep cracks
0<u<0"64 c=1+0"155u to 1.5%
0.64<u<1 c=0.811+0.450u to 1"5%
Both expressions are representations of upper bounds to the stated
accuracy. They merge continuously with the deep sharp crack solution at
TABLE 4
Pure Bending in Plane Strain
r/b Critical Constraint
factor c
0 3"2 ° 1-261
_1_
32 1 I-3 ° 1.243
±
16 17.6 ° 1-227

26. 222 A. G. Miller
1.4 i i i i i l i
1.3
Z,
u
o 1.2
c-
O
o~ 1.1
t-
O
U
I I I I I I
.1 .2 . .t. .5 .6 .0
.7 .8 .9
b
b-~r
Fig. 14. S E N B with circular root: plane strain (from Green2°).
r = 0 (c = 1.261) and the unnotched bar solution at r = oc. The depth validity
limits are not known, except for u = 0 and u = 1. The results are shown in
Fig. 14.
Ewing 34 studied the effect of g > 0 simultaneously with r > 0. For any
given rib the solution is independent of ~, provided that ~ is less than some
critical angle which depends on rib. The values of this critical angle and the
corresponding constraint factors are shown in Table 4.
2.7.4 Plane strain Mises
This gives a limit load 1.155 times the Tresca plane strain limit load.
2.8 Tension: effect of notch root radius and notch angle for fixed grip loading
Notch root radius and flank angle have no effect. The constraint factor is
always unity.
2.9 Combined tension and bending: effect of notch root radius and notch angle
Complete solutions for this are not available. For deep cracks lower and
upper bounds (sometimes widely different) are given for:
(i) large angle wedges by Shiratori and Dodd; 27
(ii) small angle wedges by Shiratori and D odd; 36
(iii) large radius circular notches by Dodd and Shiratori; 3~
(iv) small radius circular notches by Shiratori and Dodd. 38
Finite-element and experimental results are given by Shiratori and
Dodd. 39

27. Review of limit loads of structures containing defects 223
A w=lOmm
/,,0 m m 40ram A
2mm. di . 45" total notch
drilled IF angle.
hole. 0 . 2 5 m m . root
radius.
(a) (b)
I
I t mm I
[~
I
2ram
I 8ram
2b[ rrrn
/
(c)
Fig. 15. Three-point bend geometry. (al and (b) Charpy test geometries considered by Green
and Hundy; 4° (c) Charpy and lzod geometries considered by Ewing. 3"~
2.10 Three-point bending (Charpy test)
In three-point bending, there is a non-zero (discontinuous) shear force at the
minimum section, which alters the limit moment from the pure bending
value, with zero shear. Pure bending is obtained in a four-point bending test.
The Charpy test is a three-point bending geometry. Only plane strain Tresca
is considered here. (Plane strain Mises will give 1.155 times the Tresca limit
load.)
2.10.1
Green and Hundry 4° considered the two Charpy test geometries shown
in Figs 15(a) and (b), and showed that
4M
ayt2 = 1-21(1 - x ) 2 x>0-18
The reduction in the critical depth due to the presence of shear is similar to
that described in the more general treatment ofcombined bending and shear
given in Section 2.13.

28. 224 A. G. Miller
TABLE 5
Three-point Bending Constraint Factors in Plane Strain
r l b c r 1 b c
0 22 0 1"224 0-25 22 0 1'218
0-5 1"251 0-5 1"245
1"0 1-287 1"0 1"281
20 0 1"216 20 0 1'210
0"5 t'243 0'5 l'238
1-0 1"279 1"0 1"274
4M 4M
c = - - - - - - -a)
a,(t ~ (Tresca) 1"155~rr(t a) 2 (Mises)
-
r, root radius; l, half span; b, half indenter width; t, thickness = 10.
2.10.2
Haigh a n d R i c h a r d s 16 q u o t e the nearly identical result:
4M
O.yt2 = 1"22(1 - X) 2 X > 0"18
2.10.3
Ewing 34 considered the geometry shown in Fig. 15(c) and calculated the
effect of notch root radius r and indenter radius b (approximating the
indenter by a flat punch). The results are shown in Table 5, with
4M
ayt" = c(1 - x) 2
For zero indenter width this agrees with the above results.
2.10.4
K u m a r et al. 25 give the result as the pure bending solution, with no
allowance for shear. Similarly, they give the Mises plane stress solution as
being the pure bending solution. Therefore these results are not
recommended.
TABLE 6
Three-point Bending Constraint Factors in Plane Strain for Shallow
Cracks
a/t c a/t c a/t c
0 1'12 0"08 1'190 0.13 1"211
0"03 1-152 0"10 1'199 0-15 1"215
0"05 1"170 0.177 1"218

29. Review of limit loads of structures containing defects 225
1-3
0
U
o
1'2
- /"////
o
/
1-I /
/
/
/
/
/
10 I I I
0'06 0-12 0'18
a/t
Fig. 16. Three-point bend constraint f a c t o r . - - - , Four-point bend; , three-point bend.
2.10.5
The shallow crack solution (a/t < 0"18) is given by Matsoukas et al. 41 The
constraint factor c is given in Table 6 and compared with the four-point bend
result in Fig. 16. The span is given by l = 2t (see Fig. 15). In the smooth bar
limit, a / t - , O , the constraint factor c tends to the value of 1"12, in agreement
with Green. 4z
2.11 Compact-tension specimen
The limit load for the compact-tension specimen may be calculated from the
pin-loaded SENT results by a transformation given by Ewing and
Richards 22 and Haigh and Richards. x6 The geometry is shown in Fig. 17.
The transformation is
_...1
r/sE N gnCT XSEN --~ ½( 1 -+ XCT)
where n(x) - N / % t .

30. 226 A. G. Miller
CT5 1
I
!t
[ , SEN -
O SEN-----
I Lood Line
t
Fig. 17. Compact-tension specimen geometry.
2.11.1 Plane stress Tresca
n(x) = - ( 1 + x) + (2 + 2X2) l '2 l>x>0
x--* 1 n ---~y2/4
2.11.2 Plane stress Mises
n(x) = - ( ~ x + 1) + [(Tx 2 + 1)(1 + ;,)] ~/2 for l > x > 0
2
y= ~ = 1.155
1.072v 2
x~ 1 n ~ 0.268y 2 = 4
2.11.3 Plane strain Tresca
n(x) = - ( 1 + 1"702x) + [-2-702 + 4"599x 2] 1/2 for 1 > x > 0.090
x~ 1 n ~ 0"315y 2 - 1"260)'2
4
These results are s h o w n in Fig. 18.
2.11.4 Plane strain Mises
This is 1"155 times the plane strain Tresca limit load.
2.11.5
K u m a r et al. 25 give values for the limit loads which, as in the p i n - l o a d e d
S E N T case ( S e c t i o n 2.2.5), are the T r e s c a p l a n e stress f o r m u l a e ,

31. Review of limit loads of structures containing defects 227
o,7e-
0.6
O.S
TfescQ
PLane s t r a i n
0.~
N
0.3
0.2
0.1
Ol I I I
0 0.2 0./, 0.6 0.8 1.0
X
Fig. 18. Compact-tension specimen limit load.
renormalized to give the correct value as x --* 1. They are not the correct limit
loads in general, and are not recommended for use.
2.12 SEN multiaxial tension, with bending and shear
2.12.1
Jeans derived a lower bound expression (quoted by Ewing and Swingler*a):
M moment
N tensile force
ah out-of-plane stress (uniform across section)
Q mode II shear force
b ligament thickness ( t - a ) for SEN (or ( t - 2 a ) for DEN)
The geometry is shown in Fig. 19. The result is useful in cases where the
elastic stresses are available, and it avoids having to choose between the
plane stress and plane strain solution:
+-7 +

32. 228 A. G. Miller
j Surfacedefect
/1Lo
Fig. 19. Plate under multi-axial loads.
1
These expressions are based on a "nominal' Mises yield criterion, and do
not satisfy the boundary conditions at the back surface when Q #- 0. They are
a valid lower bound for double-edge notched plates, or with additional
support at the back surface.
2.12.2
Ewing (pers. comm.) gives a modification of Section 2.12.1 to allow for back
surface interaction with shear present:
0"¢=4 +(P-+L + h
N I = ( N 2+¼Q2),
~,/3
+2_Q
The plane strain case (as opposed to specified out-of-plane stresses) is
considered in Section 2.13.
2.13 Combined tension, bending and mode I1 shear
2.13.1
Ewing (pers. comm.) has derived an approximate solution for deep cracks in
plane strain under combined tension, bending and shear. When shear is
absent, the deep crack solution is valid when a/t > 0.4, but the validity limit is
not known in general. It is assumed that the tensile force acts along the
centre-line of the ligament. If it acts along the centre-line of the plate, an
extra bending moment of ½Na must be included. The solution is given in
Table 7 and Fig. 20 for the Tresca yield criterion. In the Mises case the limit
load should be multiplied by 1.155. An alternative (lower bound) solution is
given in Section 2.12.

33. Review ~/" limit loads o[" structures containing deJec'ts 229
TABLE 7
Values of L r for Edge-cracked Plate under Tension, Bend and Mode I1 Shear
(a) Table o f F expressed in terms o f m' and n'
0"0 O. 1 t)'2 0"3 0"4 0"5 0"6 0"7 0"8 0"9 I'0
0"0 1.000 1"005 1'019 1"040 1"067 1"094 1-121 I'143 1"!54 1"144 1"000
0"10 1.006 1-029 1"060 1"094 1-127 1'157 1'!80 1"!93 1"192 1"164
0"20 1"022 1-052 1"086 1'119 1-150 1-176 1"195 1-204 1"!96 1'156
0"30 1.044 1"076 1-109 1'141 1"169 1"191 1"204 1'206 1'188 1'127
0"40 1.067 1"099 1"130 1"159 1'!82 1"198 1-205 1'197 1.164 1"049
0-50 1"088 1"119 1"147 1"170 1'188 1"198 1'195 1"172 1"109
0"60 1"106 1'133 1"157 1-175 1"185 1"!84 1-167 1"119 0-892
0"70 1"117 1'140 1"158 1-168 1-168 1"152 1-108 0-971
0-80 1-119 1"136 1'146 1"145 1"127 1"080 0-874
0'90 1"103 1"112 1"109 1"085 1-018
I '00 1.000
(b) Table o f F expressed in terms o f re' and q'
0"0 0"1 0.2 0"3 0"4 0"5 0"6 0"7 0"8 0"9 1"0
0"0 1"000 1-046 1-085 1"116 1'138 1"151 1"154 1"145 1-121 1"076 1.000
0"10 0"997 1"047 1"090 1"128 1"158 1-180 1"193 1'194 1"178 1-135
0-20 0-987 1'040 1"087 1'127 1"160 1"185 1"200 1"203 1"190 1'146
0-30 0'971 1'027 1"077 1'120 1-156 1'184 1-202 1"207 1'194 1"146
0-40 0-949 t'009 1'063 1-109 1'148 1"179 1"199 1"205 1"191 1"122
0-50 0-922 0"986 1"044 1'094 1"137 1"170 1-191 1-198 1'177
0"60 0-892 0"962 1-024 1'079 1"124 1"159 1"181 1-184 1"106
0"70 0"868 0-943 1-009 1'066 1-114 1.149 1"169 1"148
0"80 0"874 0-944 1"008 1"065 1"I10 1"141 1'119
0-90 0"925 0"978 1'031 1"031 1'079 1-141
1'00 I '000
The notation is as follows: t = plate thickness; a = c r a c k depth (a/t>~ 0-4); m = bending
moment parameter = M/I'26M' for M' = a y ( t - a)-'/4; n = tension parameter = N/'N' for N' =
a,(t - a); q = shear parameter = Q/Q' for Q' = ay(t - a)/2; m' = m/r, n' = n/r, q' = q/r for r =
(nil + n 2 + q2)t/2; Lr = rF(m', n', q').
2.13.2
In the special case o f zero m o m e n t (referred to the l i g a m e n t centre-line,
E w i n g 44 h a s c a l c u l a t e d a m o r e a c c u r a t e s o l u t i o n f o r d e e p c r a c k s ) :
+ 1.03 = 1

34. 230 A. G. Miller
1 i , , = i , !
q=O
• 0.2
=E
.= o.s 0.6
IE
l0
E
, ,".. ,'x., X -
0 0.5
n = NIN e
Fig. 20. Plastic yield loci for fixed values of the mode |l shear parameter, q = Q/Q'. Here M,
N and Q denote moment, tension and shear in a combination ensuring collapse. M ' =
a) /4, N' = ay(t-- a), Q' = ~ y ( t - a)/2.
For Tresca plane strain
N1 = ay(t - a) Q I = ay(t - a)/2
(Q mode II shear resultant)
This is believed to be accurate to 2%, and can lie 17% inside the nominal
criterion:
+ =1
The yield surfaces are shown in Fig. 21. The depth validity limits are
unknown, except for Q = O.
The Mises limit load is 15% higher.
2.13.3
In the special case of zero tension, Ewing and Swingler43 have calculated
both lower and upper bounds. The lower bound is within 5% of the nominal
criterion:
+ =1
Mt = O'y(/-- a)2/4 (Tresca) QI =" f l y ( / - - a)/2
The upper bound is given in Table 8 and Fig. 22, along with the minimum

35. kN/N1
Nominal
Nominal
Per Bound
wet" Bound
~
-1 QIQ 1
NO~lna[ x 0.83
-1
Fig. 21. Yield criterion for combined tension and mode II shear. ~'~
TABLE 8
Combined Bending and Mode II Shear
(from Ewing and Swingler 43)
Q/Q= Upper bound Depth limit Upper bound Lower bound
M/M t a/t M/MI a M/M t
0.000 1.261 0.297 1.289 1.000
0.050 1.248 0.271 1.279 0.999
0.100 !-232 0-245 1.266 0-997
0.150 1.214 0.218 1-251 0.992
0-200 1.194 0.191 1.233 0.986
0.250 1.171 0.164 !-212 0.978
0-300 I. 145 0.138 I. 189 0.968
0"350 I.I 15 0-112 1.162 0.956
0.400 1.082 0-087 I. 132 0.941
0.450 1.045 0-064 1-098 0.923
0-500 1.003 0-043 1.060 0.902
0.550 0-956 0.025 1.017 0.875
0.600 0.904 0.011 0.969 0.842
0.650 0-846 0.003 0-915 0-797
0.700 0.781 0.854 0.736
0.750 0-709 0.786 0-657
0.800 0-627 0-708 b 0-561
0-850 0.536 0-618 0.447
0-900 0.434 0.509 0-315
0.950 0.3 ! 9 0.362 0.166
1-000 0-189 0.000 0-000
°These results apply to a notch at a cantilevered end.
For Q/Qt >0'8, the results are an upper bound only and cannot be exact.

36. 232 A. G. Miller
Upper B o u n d
(Notched Cantilever)
Bound
M/M Nominc]| L o w e r B o u n d
(M2/M2~.Q2/Q2=1)
I
Lower Bound
8/w 2
0"6
O.t,.
0"2
0
I I I
2/.
I I I
~l
02 or, 06 o-8 1
Q/Q1
Fig. 22. Combined bending and mode II shear (from Ewing and Swingler43).
crack depth. The upper bound is potentially exact for Q/Q ~ > 0-803 (i.e. the
slipline field is statically admissible, but it has not been constructed in full).
When Q = 0, the solution coincides with that given in Section 2.1.3.
If the notch is at a cantilever position, then the limit moment is higher, and
is also shown in Table 8. The depth validity limits for these results have not
been calculated.
The Mises load is a factor of 1"155 greater.
2.13.4
A c o m m o n approximate solution for combined tension, bending and mode
II shear is to generalize Section 2.4.1 to include shear in a Tresca yield
criterion:
~° = b2 +~ b2 +L b~ ) + 7 Lr=--~y
This is similar to Section 2.12.1 with a h = 0, Tresca shear instead of Mises
shear, and an amelioration allowed for the effect o f the crack on the collapse

37. Reriew of limit loads of structures containing defects 233
moment. As in Section 2.12.2, there is no free surface shear correction. When
compared with Section 2.13.1 over the region N > 0, M > 0, Q > 0:
Lr(2.13.1)
0-79 < < 1-17
Lr(2.13.4)
Hence the approximation is conservative (ignoring a 2% error) if a Mises
yield criterion is assumed.
2.14 Combined tension and mode III shear (plane strain)
Ewing and Swingler 43 have calculated both lower and upper bounds for the
Tresca case, with fixed grip loading (tensile force acting along the centre-line
of the ligament).
The nominal yield criterion is a true lower bound, in contrast to the mode
II case described in Section 2.13.2:
S Mode III shear stress resultant:
+ (;:7 = 1 N 1 = a , ( t - a), S l = a,(t - a)/2
An upper bound (which cannot be exact) is given by
N<S S= S t
(N) 2 N 1¢S'~ z
N>S =0
This is shown in Fig. 23.
~ U p p e r Bound
- ~~
N/N1
0-5
Lower Bound /
(N/N1)2+(sIs1)2= 1
I I I I I I I f I
0'5
s/s,
Fig. 23. Combined tension and mode III shear (from Ewing and Swingler'~)).

38. 234 A. G. Miller
t
", Line of sidegrooves
Fig.24. Geometry of inclined notch.
2.15 Inclined notch under tension (plane strain)
The geometry of this is shown in Fig. 24. Ewing 45 has considered this.
2.15.1
Unsidegrooved plane strain Tresca, pin-loading:
F= Btayn(a/t)
where B is thickness in transverse direction, Fis end load, and n(a/t) is shown
in Fig. 25 for c¢= 15 ° and ~ = 30 °.
The solution for deep cracks is exact; the solution for shallow cracks is an
upper bound.
2.15.2
Unsidegrooved plane strain Mises, pin-loading:
F= l'155Btayn(a/t)
i i i I i i i i
%
%
0.9
0.5 ~.......-~U n i vet so I s i n g l e - hinge
upper bound.
0.7
0.6 . ~
b;" ~=15,
~n 0..5 ~,
0,2 ~
0.1
I I I I I I I I
0,I 0,2 0,3 0./. 0.5 0.6 02 0,8 0.9
alt
Fig. 25. Collapse loads for ungrooved single-edge inclined notch specimens (from
Ewing~5).

39. Review of limit loads of structures containing defects 235
2.15.3
Sidegrooved plane strain Tresca, fixed grip loading (load applied through
the centre of the ligament):
~a,B!t -- a)
F = min [ayB (t - a) cosec 2ct
where B' is reduced thickness across sidegrooves.
2.15.4
Sidegrooved plane strain Mises, fixed grip loading:
. f a , B(t-- a)
F= rain
), 1"15arB (t - a) cosec 2~t
3 INTERNAL NOTCHES IN PLATES
Mainly solutions for through-thickness or extended defects are considered
here. No solutions for embedded elliptical defects are known, except for the
limited results given in Section 3.4.
3.1 Centre-cracked plate in tension
t plate width of thickness
a crack width or depth
e crack eccentricity (see Fig. 26)
h plate length
N force/width or thickness
Crock
M M
Fig. 26. Geometry of eccentric crack under multi-axial loading.

40. 236 A. G. Miller
TABLE 9
Centre-cracked Plate in Tension (values given in units of a/'~,)
(plane stress Mises)
a't h/t
0.2 0.4 0.6 >.0.71
o-l 0.650 0-753 0.900 0.900
0.2 0.390 0.654 0.800 0.800
0.3 0-230 0.530 0.646 0.700
0.4 0.145 0.425 0.538 0-600
0.5 0.100 0.312 0-427 0-500
0.6 0.076 0.225 0.338 0.400
0.7 0.065 o. 160 0.270 0-300
0.8 0-049 o. I 17 0-200 0.200
0.9 0.027 0.090 o-I oo o-I oo
3.1.1 Plane stress Tresca aJld Mises, a n d p l a n e strain Tresca
N=ay(t-a) (Ref. 16)
This is c o m p a r e d with experimental results in Fig. 27, taken from
Willoughby.17
This result is not valid for short plates (h << t). H o d g e ~6 d e m o n s t r a t e d that
it was exact for square plates (h = t). A i n s w o r t h (pets. comm.) derived an
a p p r o x i m a t e lower b o u n d solution for the case of a uniform applied stress.
This agreed with the above solution when h 2 > _ . 2 a ( t - a ) . This is always
satisfied if h/t > l / x / 2 = 0"707.
The results for short plates from Ainsworth's lower b o u n d m e t h o d are
s h o w n in Table 9 for plane stress and Mises yield criterion.
3.1.2 Plane strain M i s e s
This is 1'155 times the plane strain Tresca result.
3.2 Eccentric crack under tension and bending
3.2.1
A lower b o u n d solution which reduces to the Tresca plane stress result is, for
M - ae M (t 2 - a z - 4e 2)
(a) Nt >~t(t-a~ and ~/> 8et
M - ae M (t 2 - a 2 - 4e 2)
or(b) Nt <<'t(t-a~ and N-t~< 8et
]M + aN/2l + [(M + aN~2) z + N 2 { ( t 2 - aZ)/4 - ae}] 1 ,
Lr = 2~y[(t 2 - a2)/4 - ae]

41. Reriew O/ limit loads t?]'struc'tures containing defects 237
1.2
1.0
, , , .
N 0.8~ N ~ !!el
°
0.6
0.¢.
0.2
0
0.2 0.4 0.6 0.5 1.0
a/t
Fig. 2"/. Centre-cracked panels in tension (from Willoughby I ~). All data from Table 9. ©,
A533B steel; /~, 316 stainless steel plate; A, 316 stainless steel weld; (3, low alloy steel.
Alternatively, for
M - ae M (t 2 - a 2 - 4e 2)
(a) N t >" t(t - a-----) a n d N-t ~< 8et
M -ae M (t 2 - - a 2 -- 4 e 2)
or (b) N t <<"t(t--a----~ a n d ~/> 8et
IM- aN~21 + [ ( M - aN~2) z + NZ{(t 2 - a2)/4 + ae}] l'z
Lr = 20"y[(t 2 - a 2 ) / 4 + ae]
The geometry is shown in Fig. 26. The eccentricity e is assumed to be
positive. A positive bending m o m e n t , M, is one which tends to produce
tension at the surface closer to the crack. The positive square root sign is
taken. The choice o f f o r m u l a depends on which ligament the neutral axis is
in.

42. 238 A. G. Miller
zt~
d o o o d c~ c~
i
i 0 I
zi;~
/ /$oi~
.= ~' ~ o d c~ o o o c~ o --
I i i i
¢M
0
• . . .
o o c~ o o o d o
i i i !

43. Ret,iew of limit loads of structures containing defects 239
For e = 0 and M = 0, the solution reduces to the centre-cracked plate in
tension given in Section 3.1.1.
As e---, 1/2(t- a) the range of validity of the second solution shrinks to
zero. In the limit the first solution agrees with the single-edge notched plate
solution in Section 2.4.1.
3.2.2
BS PD6493 gives local collapse loads for embedded defects. These are based
on elastic-plastic finite-element calculations, with a criterion of 1% strain in
the thinnest ligament (here defined as b). Hence the b/t = 0 result does not
agree with the surface defect results, as described in Section 2.4. The results
are shown in Fig. 28. The geometry is shown in Fig. 26.
3.2.3
R6 Rev. 2 Appendix 247 recommends that an embedded defect should be
treated as two separate surface defects, by bisecting the defect, and assessing
each ligament separately.
No recommendation on load sharing is given. This method is very
conservative, as it ignores the resistance to rotation offered by the other
ligament, and does not allow any load shedding on to the other ligament. As
the defect approaches the surface, the limit load does not change
continuously into the single-edge notched limit load but goes to zero. For the
centre-cracked plate under tension, the R6 Rev. 2 proposal is compared with
the true limit load and some experimental results in Fig. 27. This issue of
ligament failure is similar to that in Section 1.8. Once one ligament has failed,
the defect should be recharacterized and re-assessed.
b I Ih = 1.5
t.0
"t/'%
o.s
f ~ ILE
• • • @
I ~ = , I , , , j J
0.$ l.O
bzl b I
Fig. 29. Eccentric defect under m o d e I | | loading.

44. 240 A. G. Miller
I I I I
I I I I
I I I
I I I
I "" -~1 ^ ""1
I I
I j 1 I
I I
i I I
I
I i I I
t t t t I tt t I t t t
Fig. 30. Array of eccentric defects under mode I loading.
0.5-
11500 " ~
I
0 0.25 0.5
olt
It
_11 •
2c
Fig. 31. Local collapse load for central embedded elliptical defect in plate in tension.

45. Review of limit loads of structures containing defects 241
3.2.4
Ewing ~° has considered an eccentric defect in anti-plane shear, as shown in
Fig. 29. The following quantities were calculated:
q. stress required to spread plasticity across shorter ligament, assuming
strip yielding model
rLE value of v~. estimated from elastic stress resultants
rG stress needed to spread plasticity across both ligaments (constraint
factor is unity)
The same numerical results apply to the mode I tensile analogy shown in Fig.
30, and may be considered as an approximation to the mode I loading of a
single strip with an eccentric defect.
3.3 Eccentric crack under tension, bending and out-of-plane loading
The lower bound solution in Section 3.2 may be generalized to include out-
of-plane tension and shear (but not out-of-plane bending). The geometry is
shown in Fig. 26. Free surface shear stress effects have been ignored (see
Section 2.12). Let
N' = N- 1/26h(t - a) M ' = M + l/2ahae
Then
(a~ + 3/4a~ + 3r2) t~z
Lr m (with a Mises shear term)
O'y
where
M ' + aN'~2 + { ( M ' + aN'~2) 2 + {N')2[(t -' - a2)/4 - ae]} l'z
a~ = 2[(t 2 - aZ)/4 - ae]
a. is the out-of-plane tensile stress and r-" is the sum of the squares of the
shear stresses.
For the assumed stress distribution to be valid
N'>O M'>O
For a~ = r = 0, this reduces to the solution given in Section 3.2.1.
3.4 Embedded elliptical defect in tension
The only results known to the author are those for the local ligament
collapse load for a central elliptical embedded defect in a plate in tension
given by Goerner. 4s A simplified strip yielding model was used, and the
calculated load was the load at which yielding first extended across the
ligament at the thinnest point. The calculations are analogous to those for
surface defects quoted in Section 5.1.3, and the results are shown in Fig. 31.

46. 242 A. G. Miller
4 DOUBLE-EDGE NOTCHED (DEN) PLATES
t thickness b ligament thickness ( t - 2 a )
a crack d e p t h u b/(b+r)
x a/t ~ n o t c h flank angle
r n o t c h r o o t radius c constraint factor
T h e g e o m e t r y is s h o w n in Fig. 32.
4.1 Bending
4.1.1 Plane stress Tresca
4M
c-- =I
ay(t -- 2a) 2
4.1.2 Plane stress Mises
4M
C--
ay(t - 2a) 2
This is not k n o w n but must satisfy 1 < c < 1.155.
4.1.3 Plane strain Tresca 2°
4M
c- - 1-38 x > 0"168
o'y(t -- 2a) 2
F o r shallow cracks this must be c o n t i n u o u s with the u n n o t c h e d bar result
(e= 1).
4.1.4 Plane stra& Mises
This is 1"155 times the plane strain Tresca limit load.
4.2 Tension
U n l i k e the S E N T geometry, there is no m o m e n t due to the eccentricity o f the
tensile force.
4.2.1 Plane stress Tresca 49
N
C.~- =1 O<x<l
O'y(t - 2a)
4.2.2 Plane stress M i s e s 49
N
C=
a y ( t - 2a)
c = 1"155 0"143 < x < 0-5
c = 1 + l'08x 0<x<0-143

47. Review of limit loads of structures containing defects 243
N
MA-
0 "
I
I
I
Q h Q
,C
I
I
I
I
t
M
N
Fig. 32. DEN geometry. N, Tension: M, bending moment; Q, mode II shear.
The deep crack solution is exact. T h e shallow crack solution a n d the
transitional value o f x are a p p r o x i m a t i o n s .
4.2.3 Plane strain Tresea 50
N
C--
try(t - 2a)
e = 1 + In (1 - x
_--2~x)l 0 < x < 0.442
rc
c = I + }- = 2.57 0.442 < x < 0-5
x--,O c-, l + x
The deep crack result comes f r o m the P r a n d t l fan slipline field.
4.2.4 Plane strain M i s e s
This is 1"155 times the plane strain Tresca limit load.

48. 244 A. G. Miller
4.2.5
K u m a r et aL 2s give formulae which are not the correct limit loads. These
results are not recommended for use.
4.3 Combined tension and bending
The general solution for combined tension and bending is not known. A
lower bound solution, exact for Tresca plane stress, may be obtained by
applying the Tresca plane stress solution for plain beams to the reduced
section width:
[2M[ + [ 4 M 2 + N 2 ( t - 2a) 2]~ '
L r =
ay(t - - 2 a ) 2
For a given ligament thickness and ligament load, the single-edge notched
solution will be a lower bound to the double-edge notched case.
4.4 Bending: effect of notch angle
4.4.1 Plane stress Tresca
4M
-1
o'y(t -- 2a) 2
4.4.2 Plane stress Mises
Not known but 1 ~<c~< 1"155.
4.4.3 Plane strah7 Tresca z°
¢--
4M
Cry(t -- 2a) 2
Deep cracks
0<:(<30 ~ c = 1.380
30 -~< ~ < 73.6 ° c = 1"380 - 0.280(:( - 7z/6)a to 0"2%
73.6 ° < x < 90 ~ c= 1+r~t2-~
Green's results are upper bounds. The intermediate range of:t equation is a
numerical fit to his bound. This merges continuously with the deep sharp
crack result at ~ = 0 (c = 1"380) and the unnotched bar result at ~ = rt/2. The
depth validity limits are unknown. The results are shown in Fig. 33. Dietrich
and Szczepinski 35 give the complete slipline field for ~--75 ~, and their
constraint factor is the same as above.
4.4.4 Plane strain Mises
This is 1"155 times the plane strain Tresca limit load.
A discussion o f combined tension and bending in plane strain for large
notch angles and deep cracks is given by Shiratori and Dodd. z7

49. Review o f limit loads ~/" structures containing d~/bcts 245
1.1, l !
,..1.3
0
"6 ,.2
e.
o I.I
1 ! I
90 eO ?0 6~0 5'0 z:o 3~0 zo I=0
Fig. 33. DENB with V-notch: plane strain (from Green2°).
4.5 Bending: effect of notch root radius
4.5.1 Plane stress Tresca
4M
=1
ay(t - 2a) 2
4.5.2 Plane stress Mises
¢--
4M
o'y(t - 2a) z
Not known but 1 <c< 1"155.
4.5.3 Plane strain Tresca z°
4M
C--'-.
¢ry(t - 2a) 2
0<u<0-398 c=1+0"256u to I %
0"398 < u < 1 c -- 0-914 + 0-467u to 0-2%
G r e e n ' s results are u p p e r b o u n d s , a n d the e q u a t i o n s are r e p r e s e n t a t i o n s o f
these b o u n d s to the s t a t e d a c c u r a c y . T h i s m e r g e s c o n t i n u o u s l y with the d e e p
s h a r p c r a c k s o l u t i o n at r = 0 (e = 1"38) a n d the u n n o t c h e d b a r solution at
r = ~ . F o r validity
1
1 - 2x > pC > 1-30 x > xo(r/b ) > 0"115
T h e e x a c t values o f x o are u n k n o w n . T h e results are s h o w n in Fig. 34.

50. 246 A. G. Miller
m
1.3
u
°1.2
C
0
C
0
1
0 .1 .2 .3 ,t. .5 .6 .7 .8 .g 1.0
b
b+r
Fig. 34. DENB with circular root: plane strain (from Green-'°).
4.5.4 Plane strain Mises
This is 1"155 times the plane strain Tresca limit load.
A discussion of c o m b i n e d tension and bending in plane strain for large
root radii and deep cracks is given by D o d d and Shiratori. 3~
4.6 Tension: effect of notch angle
4.6.1 Plane stress Tresca s~
N
e --1
ay(t - 2a)
Hill showed that the constraint factor is i n d e p e n d e n t o f notch shape.
4.6.2 Plane stress M i s e s 49
N
C=
ay(t -- 2a)
< 70"5 ° shallow c = 1 + l'08x 0<x<0"143
deep c = 1-155 0.143 < x < 0.5
c~> 70-5 ° shallow c = 1 + 1.08x 0 < x < 0-143 sin [(re/2 - :0, 0.217]
deep c = 1 + 0.155 sin [(rc/2 - ~)/0.217]
0"143 sin [(rc/2 - e)/0"217] < x < 0"5
(:~ in radians)
These are a p p r o x i m a t i o n s to numerical results. The deep crack results were
given by Hill 5~ a n d F o r d a n d Lianis. ~8 The results are identical with the
sharp crack results for ~ < 70.5 °, and give the u n n o t c h e d bar results for
= re/2. The results are s h o w n in Fig. 35, with b o t h upper and lower bounds.

51. Review of limit loads of structures containing defects 247
1.15
upper bound
f bound
o 1.10
N ros
C
0
(..)
1.0
90 80 70 60 S 4 30 20 I0 0
=,c=notch angle ,~
Fig. 35. DENT with V-notch: plane stress Mises (from Ford and Lianis~a).
4.6.3 Plane strain Tresca s°
N
ay(t - 2a)
e =/2 - = - - 1
shallow c=l+In 1-x
x < x o = 2e=/2 _= _ 1
deep c = 1 + r~/2 - :~ x > x o
T h e t r a n s i t i o n o c c u r s w h e n the t w o e x p r e s s i o n s are equal, a n d so the s m a l l e r
c o n s t r a i n t f a c t o r a l w a y s applies. E w i n g 52 generalizes this result to a l l o w for
r > 0. T h e results are identical with the s h a r p c r a c k results for ~ = 0, for b o t h
d e e p a n d s h a l l o w cracks, a n d with the u n n o t c h e d b a r results for :~ = re/2.
4.6.4 Plane strain Mises
T h i s is 1-155 times the p l a n e strain T r e s c a limit load.
4.7 Tension: effect o f notch root radius
4.7.1 Plane stress Tresca 5~
N
e= =1
ay(t - 2a)
Hill s h o w e d t h a t the c o n s t r a i n t f a c t o r is i n d e p e n d e n t o f n o t c h shape.
4.7.2 Plane stress Mises 5t
Deep cracks
b/2r < 1"071 e = 1 + 0"226b/(b + 2r)
b/2r > 1"071 c = 1"155 - O.080r/b
T h e s e are u p p e r b o u n d s a c c u r a t e to 1"8%. F o r d a n d Lianis ~8 give similar

52. 248 A. G. Miller
1.15
Hill's upper b
o
1.10
//~. Lower.
e- 1 . 0 5
o
1.0 I
0 0.1 0.2 0.3 0.4 O.S 0.6 0.7 O.S 0.9 1.0
b
b÷r
Fig. 36. DENT with circular root: plane stress Mises (from Ford and LianisLS).
results. T h e y merge with the deep s h a r p n o t c h solution at r = 0 ( c = 1"155)
and with the u n n o t c h e d b a r solution at r = vc. T h e d e p t h validity limits are
not k n o w n , except at r = 0 and r = c~. T h e results are s h o w n in Fig. 36, with
b o t h u p p e r a n d lower bounds.
4.7.3 Plane strain Tresca 5z
N
c- /. = min [7z/2, In (1 + b/2r)]
ay(t - 2a)
deep n o t c h e s (exact)
t > b(2e z - 1) - 2r(e ~ - 1) 2
small b/r:/. = In (1 + b/2r)< ~/2 angle at n o t c h that has yielded
c = (1 + 2r/b)ln(1 + b/2r)
This result was given by Hill: 53
large b/r: In(1 + b/2r) > 7t/2
c = 1 + ~/2 -- 2r/b(e ~"2 _ 1 - ~/2)
shallow notches ( a p p r o x i m a t e )
t < b(2e z - I) - 2r(e z - I) 2
( 2r 2rt"l'/2 (~_rr) [ b b( 2r 2rt'~] '/2
c= 1+ b b2 j + 1+ In l+2r-2r 1+ b t,-'J_]
W h e n r = 0 the solution is identical to that o f Ewing and Hill 5° for s h a r p
notches, b o t h d e e p and shallow. F o r u n n o t c h e d bars
r= m Z=0 tc=b
T h e deep n o t c h solution gives c + 1. T h e shallow n o t c h solution limit

53. Review of limit loads of structures containing defects 249
depends on the order in which the limit is taken, but gives c ~ 1 if r--, oc is
taken last. Ewing 52 also gives the effect of ~ > 0.
4.7.4 P l a n e s t r a i n M i s e s
This is 1"155 times the Tresca plane strain limit load.
4.8 Staggered notches under tension with restrained rotation
Connors s4 gives an approximate solution for the geometry shown in Fig. 37,
with the notation:
a = crack depth (cracks of equal depth)
d = crack separation
t = plate thickness
N 0 = fly/
Ny = limit load
Ny = min (Ni, NH)
a r i d 2 + (t -- 2a) z]
N~ = [ 3 d 2 + (t - 2a) 2] t/2 using the Mises yield criterion
N, is the pin-loaded S E N T result from Section 2.2. The experimental results
are shown in Fig. 38 for the limit load based on a deformation criterion.
For d = 0 this reduces to the Tresca plane stress D E N T solution (despite
the use of the Mises yield criterion).
4.9 Combined bending and mode II shear
This has been calculated for deep cracks in plane strain by Ewing and
Swingler. 43 The results also apply to the case where the cracks are at a
cantilevered end. Lower and upper bounds are shown in Table 10 and Fig.
39. The 'nominal' yield criterion is also shown:
+ =1
M1 = ~,(t -- 2a)2/4 (Tresca) Q1 = cry(t- 2a)/2
This is within 5% of the lower bound.
The upper bound is potentially exact, but is an incomplete solution. In the
zero shear limit, it agrees with the solution given in Section 4.1.3. The depth
validity limits are also shown in Table 10. They are reduced by shear.
The Mises limit load is greater by a factor of 1.155.

54. d
L =-I
i i
I I
' ..... (_ _ ~a .....
tr I- -/- T
',, /
Location of defects
Fig. 37. Typical specimen with staggered defects (from Connors54).
1 .0
.~.= d
.9 No '/'Jt
.?
o
+t
Z Olt =0.25
0
0
.5
t t ~ °,,:o.37+
.¢,
0
;_ ~ °,,=0~
}-
iI.O
i
2.0
I
3.0
~
Relative separation of defects, d l t
§
I
~.0
I
5.0
at t =0.7
Fig. 38. Experimental results for bars with multiple defects and theoretical predictions
(from Connors54). - - , Theoretical predictions.

55. Review o f limit loads o f structures containing defects 251
Upper Bound
M/MI
Nominal Lower Bound
I .(M21MI 2 ÷ O21012--1)
Lower Bound
8/~ 2
0-6
o., -
0.2 !- '1
j 2/~ 1
o i i I ] i
0-2 0"~ 06 0-8 I
Q/Q1
Fig. 39. Combined bending and mode II shear (from Ewing and Swingler~3).
TABLE 10
Combined Bending and Mode II Shear
(from Ewing and Swingler43)
O/O, Upper Depth Lower Q,"Q I Upper Depth Lower
bound limit bound bound limit bound
M/M t 2a/t M/M 1 M/M t 2a/'t AI/M t
0-000 1'380 0"336 1"000 0-550 1-020 0-051 0"875
0"050 1-358 0"314 0"999 0'600 0"970 0'028 0"842
0"100 1'334 0"290 0"997 0"650 0"915 0"011 0.797
0-150 1-308 0'266 0-992 0-700 0-854 0-001 0"736
0'200 1-281 0-241 0'986 0-750 0"786 0-657
0'250 I "251 0-215 0'978 0-800 0"708 0-56 I
0-300 1"220 0-188 0"968 0-850 0-618 0.447
0-350 I' 185 0" 160 0"956 0'900 0-509 0"315
0"400 1"149 0"132 0"941 0"950 0"362 0"166
0"450 I" 109 0' 104 0"923 ! "000 0-000 0"000
0-500 I "067 0.077 0'902

56. 252 A. G. Miller
M
_.U
n
t
l Iut°'t,
b /N )
M
I ..... +
1
Fig. 40. Asymmetric double-edge notched plate.
4.10 Combined tension, bending, mode 11 shear and out-of-plane stress
The solution given by Jeans, 43 quoted in Section 2.12.1, is a true lower b o u n d
for this case (with uniform out-of-plane tensile stress across the section).
4.11 Combined tension and bending: asymmetric notches
The geometry considered is shown in Fig. 40. Ewing (pers. comm.)
constructed a Tresca plane stress lower bound solution as follows. With
notation as in Fig. 40
Mt = M + Nat/2
is the moment referred to the middle of ligament h I (= t - at). Assuming that
the cracks are able to support compressive stress, then
L r = [ 2 M t + (4M/- + N 2 h~) 1 2 ]/(ay/-,t)
"~ "~ 2 ,
provided that the compressive region is at least as deep as crack a_,. The
height h of this region satisfies
- h a y + (h t - h)cTy= N~.om,p~c= N,/L r
so that
2h = h t - N / L , a y ~> 2a_, (26)
a;t 'tl
N
t r
bl
dl
+ d2
:x: (in c o n t a c t )
t J ~c12
Fig. 41. Asymmetricdouble-edge notched plate alternative solution.

57. Review of limit loads of structures containing defects 253
Ifeqn (26) fails, ignore material below some ligament 'b' lying between b~ and
i.e. solve for b and L r the simultaneous equations
b~ - a z,
L r = {2M" + [ 4 M ''2 + N 2 b 2 ] t / 2 } / u y b 2 b = 2a~ + N/Lray
where
a'~ = a z - b I + b M " = M I - N ( b I - b)/2
Alternatively, for very deep cracks a2 in compression, assume that only the
outside part 'x' is compressed and that the system is equivalent to an internal
crack (see Fig. 41). At collapse
N/L r = ay(bt - a2 - x ) M/Lr = ¢ry[(bl - a2)dt + x d 2 ]
which can be solved for x and Lr as unknowns. This gives an alternative
lower bound.
5 S H O R T S U R F A C E C R A C K S IN PLATES
5.1 Wide plates in tension
Ligaments in finite length cracks are stronger than ligaments in extended
defects, as they derive support from the adjacent uncracked plate. If
ligament failure is the subject of concern, then this 'local' limit load goes to
zero as the ligament thickness goes to zero. This is in contrast to the 'global'
limit load, which would tend to the through-cracked plate limit load (as in
Section 3) as the ligament thickness tended to zero. Moreover, for wide plates
(width >>defect length) the defect has no effect on the global limit load.
a defect depth (see Fig. 42)
2c defect surface length
t plate thickness
W
2c P
Fig. 42. Geometry of surface defect.

58. 254 A. G. Miller
1.0 D
0.8
0.~ 0.5
/'~)e f f
, , ,
0 0.2 0 :, 06 0.8 1.0
(li t
Fig. 43. Ligament correction parameter as a function of a/t (from MilneSS).
5.1.1
R6 Rev. 2 recommends that short surface cracks may be treated as extended
defects with an equivalent depth given by
__
0.1 < 2--~< 0.5
o 2t(2c+ t)
O<ff<0.8
t
(t)e=-at --2ca<0"1
No guidance is given for deep defects with a/t > 0"8. This is shown in Fig. 43.
(There is a misprint in Fig. A2.2 in R6 Rev. 2 in the inequality limits.) There is
not a smooth transition between short defects and extended defects, and the
recommendation is arbitrary.
5.1.2
Chel156 proposed a transformation
a[ 1 - ( l/f)] where f = (1 +~-)2cZ'~1'2
ae = 1 - (a/tf ) <~ a
for extended cracks (c = oo) ae=a
for zero length cracks (c = 0) ac=0
for through cracks ae=a=t

59. Review of limit loads of structures containing defects 255
He proposed that this formula applied to all geometries, not only plates. This
transformation is analogous in form to the Battelle formulation in Section
8.2.3, which may be written
a[ 1 - (l/M)]
ae = 1-(a/tM)
where M is a function of both c/t and R/t (R is the cylinder radius):
C2 '~1/2
M- 1 + 1"05~-~-,/
CheWs transformation gives a lower limit load for cylinders than the Battelle
transformation, as f > M. This transformation is the simplest rational
function with the above three properties.
5.1.3
Mattheck et al. 57 propose an expression for ligament yielding based on
Dugdale model calculations. Their expression is tr = arM, where
M = (1 - I - 1.9071 1 + 1.5151(a)°'16596(/)2
1 52(a']214'O(a'] 3
1
x [ - 0.74 + 3.855 a - 3.825(a)2 - 2.89(a)3
+ 4"356(ayl}[1- (t)"4° 1
This equation can be applied for a/c < 0-7; ~r is applied membrane stress.
This formula is shown in Fig. 44(a) and compared with their detailed
numerical results. The results are compared with the above expressions from
R6 and Chell in Fig. 44(b). It can be seen that in general the Mattheck result
is most conservative and the R6 Rev. 2 result is least conservative. The R6
result has been plotted beyond the claimed validity limits for a/t.
5.1.4
Miller 9 derived a semi-empirical model for ductile failure (i.e. at L m~x) of
surface defects and concluded that the reference strain at failure was
k t 1-a/t
4 c a/t

60. 256 A. G. Miller
t.0
lo'f 0.5
0
o.,-----'~~ ale
0.7
0.5
0.3
O O. 5 1. 0
oil
(a)
1.0
o ....... ~ 1/fl'
0.5 i.O
olt
(b)
Fig. 44. Effectof surface crack length (from Mattheck et al:~). (a) - - - , Fitted equation:
, numerical results. (b)'.-, Chell;---, Harrison ( R 6 1 ; - - , present method.
where k is a material c o n s t a n t between 0.4 and 1"5 for mild steel. This strain
m a y be used to give an a p p r o p r i a t e stress for use with the limit load.
5.1.5
If this strain (Section 5.1.4) is below the yield strain, then Miller
r e c o m m e n d e d t h a t a simplified line spring model could be used to estimate
the load at which the ligament goes plastic. F o r pin-loading with remote
load cry, this is given by
O"
x (I a/t)[(~mm + A)(Z%b + Aft) z
GF A(O~bb -t- Aft)
where
2c 1 l+v
m~-- m

61. Review of limit loads of structures containing defects 257
(i- ~-)z =~i (÷)
(~.)z
2[ mm
mb= bm
bb
oI [ I I I I
o 0.2 O.t, 0.6 0.8 1.0
OIt
Fig. 45. Spring compliance (SEN).
a n d ~ is s h o w n in Fig. 45. ~ m a y be c a l c u l a t e d f r o m f o r m u l a e g i v e n b y
E w i n g : 5s
x =- a/t y -- 1 -- x ~ij = nlij
I m m ( x ) = O ' 6 2 9 4 4 x 2 ( l + 5"474xZ + 1 3 " 3 8 x 4 - - 3 2 x S + 58"32x6) ifx<0"5
= (0"629 4 4 / y 2 ) [ 1 -- 2"944)' + 1"0834y 2 In (1/2y) + 2"667) '2] if x > 0"5
Imb(X) = 0"209 8 lx2(3 - 2"4x + 9"487x 2 + 43"4x 3 -- 142"07x 4
+ 173"6x 5 -- 27"89x 6) if x < 0"5
= (0"209 81/)'2)(1 -- 1"4723' + 0"370 6 4 y 2) if x > 0"5
lbb(X) = 0"069 938xZ(9 -- 14"4X + 46"98X z -- 46X 3 + 89"02X 4
-- 184X 5 + 193"9X 6) if X < 0"5
= (0"069 938/y2)(1 -- 1"3404) '2) if X > 0"5

62. 258 A. G. Miller
5.1.6
An alternative geometrical approach suggested by the Welding Institute
(pers. comm.) is that the stress is unloaded from the crack on to the nearest
part of the cracked structure. The critical load is taken as that which the
thinner ligament first yields, using a local fixed grip criterion:
(1 - x)(1 - x + 2R/t)a m - ab/3
af = 1 - 2x + 2R/t
R is the radius of curvature of the crack front (c2/a for ellipse).
5.1.7
It is recommended that the global collapse load is used if the criterion given
in Section 5.1.4 is satisfied. Otherwise the local collapse load given in Section
5.1.5 should be used.
The above solutions have only considered a single surface defect. They all
have the limiting behaviour
C O"m
t o'f
£ (7 m (I
- >> I ---* I - -
t af t
Therefore it is suggested that in the case of an extended defect of variable
depth, the ligament thickness should be taken as an average thickness over a
length equal to the plate thickness, and a local fixed grip criterion used:
am- 1 c~
o'f [
where ~ is the average crack depth. This suggestion is provisional only.
5.2 Narrow plates in tension
When the plate width is not much greater than the defect length, the global
collapse load limit is reduced by the presence of the defect. For rectangular
surface defects in a plate under fixed grip loading, the constraint factor is
unity:
F= ayA
F tensile force
A net-section area in plane of defect
For non-rectangular defects this will give a lower bound.

63. Review of lirnit loads of structures containing defects 259
5.2.1
A review of CEGB and Welding Institute test results is given by Miller. 59
The degree of gtrain hardening is observed to increase with increasing
ligament thickness.
Miller 59 gives the nominal strain at failure as
kt(t - a)
4ca[ 1 - (2c/w)] "
w plate width
k material constant ~0.4-1-5
A lower bound to the final plate failure load after ligament snap-through
is given by F = a,A o, where A o is the net-section area without the ligament.
5.2.2
Hasegawa et al. 6° observed a similar increase with ligament thickness of the
net-section stress at the onset of crack penetration. They empirically put the
ligament stress cr~ and the stress cr~ in the rest of the plate as
~rl = (1 - R)crf (R = reduction of area in tensile test)
tro = tru - (a. - ar)(a/t)
A lower bound to the final plate failure load was given by
F = A o m i n l a , , a f + ( a . - O'f)( 1 --a/t~210"9
}_]
which is slightly lower than that given in Section 5.2.1.
5.2.3
Mattheck and Goerner 6t used a strip yielding model where the stress along
the crack front and along the ligament centre-line was a u, just before
ligament rupture, whereas the stress at the end of the plastic zone at the
surface is reduced to the yield stress. Although detailed results were not
presented, this will also give an increase of net-section stress with ligament
thickness. Agreement with ligament rupture test results was good.
5.2.4
Munz 62 gives a review of surface cracks. He also reports further plate tests
of Goering, which agreed with the hardening models of Sections 5.2.2 and
5.2.3, but where the maximum load was underestimated by using flow stress.
5.2.5
The above are concerned mainly with the ductile instability cut-off at Lr
max.
Miller t2 reviewed published J calculations for surface defects in plates in

64. 260 A. G. Miller
tension. He concluded that using net-section (global) collapse gave better
reference stresses fo/" J estimation than using local collapse.
It is recommended, therefore, to use the global collapse load for J
estimation. Provided the strain criterion criterion of Section 5.2.1 is satisfied,
it may also be used for ductile instability assessment. If it is not satisfied, then
a local limit load should be used for ductile instability.
5.3 Plates in bending
There is no generally accepted limit moment for this geometry. The
geometrical transformations of Sections 5.1.1 or 5.1.2 might be used.
Alternatively, the simplified line spring model used in Section 5.1.5 may be
adapted, along with an appropriate ligament yield criterion, such as that
given in Section 2.4.3.
6 R O U N D BARS
6.1 Bar with axisymmetric sharp notch under tension
R maximum radius
b minimum radius
F axial force
The Tresca yield criterion is used:
unnotched
F = ~/9 20"y
deep sharp notch 63'6"~
F
c-- - - = 2 " 8 5
- h R<0"31
7~h20"y
or similarly v
F _ ~'2.85 b R <0.35
4'--
rtb2ay ( R / b h R > 0"35
The deep solution is exact, but the shallow solution is an approximation.
This shallow solution is continuous with the unnotched bar result and the
deep notch result. Ewing's results are quoted by Haigh and Richards, ~6 and
are thought to be accurate to 6%.
6.2 Bar with axisymmetric V-notch under tension
The solution is given by Szczepinski et al. 65 The constraint factor is shown in
Fig. 46 and agrees with Shield's result. The depth requirements are shown in

65. Reciew o/'limit Ioad~ 01 structures containing de/i'cts 261
C (Shield)
heotetical
2.6 -%,,curve 2=.
2.&
2.2 ~ f>p.
2.0
~. "%%.~ 2b Moteriol oluminium
1.8 "'~
16 f u ..L / %
. 0"~
1.4 % ~
1.2 '~'
1.0 J i I I I ~1 ,
15° 30" 45 ° G0" 75" 90 °
(7,.
Fig. 46. Theoretical and experimental values of the constraint factors. ©, Axial symmetry
calculated points: A , experimental ./;r points (yield point); ff], experimental fu.~. points
(ultimate load). (From Szczepinski et al. 65)
Fig. 47 and are slightly less restrictive than those give by Shield.
Experimental results are also shown in Fig. 46.
A lower bound that is within 4% o f the results in Fig. 46 is
F 3'7:~
c - - ~,rcb2 - 2"85 - -
a - (x in radians)
7~
An approximation to the depth requirement is
R 3-88:(
-- > 2"94 - - -
b ~z
6.3 Bar with axisymmetric round notch under tension
b minimum radius
r notch root radius
F axial force
R i b 3.0,
2.6
2.6
2. t,
2.2
2.0
1.8
1.6
1.4
1.2
1.0 .-.-.~-
0 30 e 60 ° 9 0 ° l z 0 " l S 0 t 180 •
Notch angle 20(
Fig. 47. Theoretical values of the R/b ratio for V-notched bars (from Szczepinski et al.65).

66. 262 A. G. Miller
TABLE I I
C o n s t r a i n t Factors for Axisymmetric Bars with a R o u n d N o t c h
under Tension
h/r Bridgman 66 Siehe168 S:czepinski et al. 6~
0 I I I
I/3 1.078 1.083
1/2 I'115 1.125
I 1-215 1.250
2 1.386 1.500
2"5 1.65
3 1.524 1.750
4 1.649 2.000
Mises yield criterion (except for Szczepinski et al., 65 who uses Tresca):
7~b2o.y (l d- In + (Bridgman 66)
F b
¢ -- ~b2o.y - 1 + ~ (Davidenkov and Spiridinova 67 and Siebel 6s)
These both reduce to a constraint factor of unity for an unnotched bar. The
formulae are compared numerically in Table 11. The Davidenkov form is
the small b/r limit of the Bridgman formula. At large b/r the constraint factor
must be limited by the sharp notch result:
b/r = ~ c = 2"85
Szczepinski gives an approximate deep crack validity limit:
-->2"95 1-1-68 -<0.4
b b
R r
-->1 -=~
b b
Some geometries with longer notches were considered by Szczepinski
et al., 65 and the constraint factor is shown in Fig. 48, along with the
experimental results. (There is an inconsistency in the description of the
geometry in the paper.)
Hoffman and Seeger 69 give a finite-element result:
R r 1
= 2 b - 11"~ - 0"085 c = 1"90
This is bounded above by Ewing's result for r = 0 in Section 6.1 (c = 2), as it
should be. It is bounded below by Szczepinski's result for rib = 0-4 (c = 1"65),
also as it should be.

67. Review of limit loads of structures containing defects 263
c'"
I,., ,_~ ,~ ,_-t.,~
• ~ . I Ld Material:
1,5 ~/theoret#cal curve ~ mild steel
IX
~1"1 ,~....~,,
"~...~n, e
0,, , . . . .
0./* O.G 0.15 1.0 1.2 t.t, 1.6 1.8 2.0
d/b
Fig. 48. Theoretical and experimental values of the constraint factors. O, Axial symmetry
calculated points; A, experimentalfyp points; 0, experimentalfu.Lpoints. (From Szczepinski
et aL 65)
6.4 Bar with axisymmetric notch under torsion
b minimum radius
T twisting m o m e n t
The constraint factor is unity for all notch geometries:
3T
c=/tb3o.
~ - 1 Tresca (Walgh and Mackenzie 7°)
3x/3 T
c = .---=-=-= 1 Mises
_
2rcb~cT,
6.5 Round bar with chordal crack under bending
R bar radius
a crack depth
b ligament depth ( 2 R - a)
M L collapse bending m o m e n t
M o collapse value for uncracked bar
T L collapse twisting m o m e n t
To collapse value for uncracked bar
y b/R
Ir v 3 2R
Crack depth ,.a
Ligament depth, b
t
Fig. 49. Schematic diagram of a bar containing a chordal crack (from Akhurst and
EwingVn).

68. 264 A. G. Miller
ML
1.0
0.9
6)"
0.8
(P '
0.7
0.6
O.S
0.4
0.3
0.2
0.1
01 I l =
0 0.1 0)2 0.3 01.4 O'.S 016 0~7 0.' 0.9
al 2R
Fig. 50. Lower bound bending moments for p.lastic collapse of chordally cracked bar in
bend (from Akhurst and Ewing7~). M L. Bending moment for plastic collapse; Mo, bending
moment of untracked bar at plastic collapse; a, crack depth; R, bar radius.
The geometry is shown in Fig. 49. Akhurst and Ewing v ~ give a lower bound
Tresca solution, shown in Fig. 50 and Table 12 for O<b/r< 1:
uncracked Mo= 4R3ay/3
deep cracks ML/Mo= (0"315 - 0"05)')3 .5 2 b< R
This fits the tabulated results to 1//2%.
6.6 Round bar with chordal crack under torsion
Notation as above. The exact Tresca solution was determined by Akhurst
and Ewing. vl As for the S E N T limit load, the value depends on the end
constraints, and is greater for the more constrained case. If the ends are
constrained in their original straight line, then the restraints carry a sideways
force, parallel to the crack front. If the shaft axis is unrestrained, the limit

69. Review of limit loads of structures containing defects 265
T A B L E 12
Normalized Collapse Loads for Chordal Crack
a/2R MtjMo (bend) TtJT o (torsion) Tt./To (torsion)
lower bound constrained ends free ends
0 1 1 !
0-05 0.958 0.973 0.964
0-1 0.889 0.928 0.902
0-15 0-810 0.875 0.829
0-2 0-725 0.819 0.749
0-25 0.640 0.762 0.667
0.3 0-556 0.705 0-584
0-35 0.475 0,651 0.504
0-4 0.400 0.598 0-427
0.45 0.329 0.548 0-355
0.5 0-265 0.500 0.288
0'55 0.208 0-452 0.227
0.6 0.158 0.402 0,174
0-65 0.116 0.349 0.128
0.7 0.080 0 0-295 0.088 9
0-75 0-051 6 0-238 0.057 7
0.8 0.0300 0-181 0,033 7
0-85 0-014 8 0.125 0.016 8
0.9 0-005 5 0.072 0 0-006 2
0.95 0,001 0 0-026 9 0,001 1
1 0 0 0
torque is reduced. The results for both cases are shown in Fig. 51 and Table
12:
uncracked TO= n R 3 a y / 3
6.6.1
Deep crack, constrained:
T L / T o = (0"9 - 0"5y + 0 l y 2 ) y 3/2 b< R
6.6.2
Deep crack, unconstrained:
T L / T o = (0"360 - 0.072y)y 5'2 b< R
These approximations are accurate to 1/2%.
6.7 Round bar with chordal crack under combined torsion and bending
Akhurst and Ewing ~ give a lower bound formula:
( M / M L ) 2 + (T/TL) 2 = 1

70. 266 A. G. Miller
TL
To
0.9
0.8
Fully rigid bar.
0.7
of shear = Bar <axis
0.6
0. S
0.4
0.3
0.2
Fully flexible bar
o.I
A x i s of s h e Q r ~
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
al2R
Fig. 51. Lower bound torque or plastic collapse of chordally cracked bar subject to a
torsional loading at its ends (from Akhurst and EwingV~). TL, Plastic collapse torque; To,
plastic collapse torque of uncracked bar; a, crack depth; R, bar radius.
where ML and TL are taken from Sections 6.5 and 6.6 respectively. This
applies for both constrained and unconstrained torsion.
7 G E N E R A L SHELL S T R U C T U R E S
7.1 Shell parameters
The above plane stress and plane strain solutions for edge notched plates
have had a detailed treatment of the through-thickness stress variation.
With shells the effect of curvature is an extra complication, and the through-
thickness stress variation is usually reduced to direct stress resultants and

71. Ret,iew of limit loads of structures containing defects 267
bending moments. The solutions are usually expressed in terms of a shell
parameter p:
c
p = (Rt)l/2
where c = characteristic defect length, R = characteristic shell radius and t =
thickness.
The simplest shell structures are those with membrane stress solutions
(e.g. spheres and cylinders). Considering pressure loading, the limit pressure
tends to the m e m b r a n e solution for the uncracked shell as p --, 0, and to the
membrane solution for the cracked shell as p-~ ~ (this will be zero for
through-cracked shells). The limit pressure is a non-increasing function
ofp.
The tendency for the limit pressure to approach the membrane solution
for the cracked shell as p increases may be demonstrated on the assumption
that plasticity is confined to a shallow region round the crack. Then in
Cartesian coordinates the equilibrium equations controlling are (neglecting
terms of order t/R)
~'2M U
c~x, ~xj + ~qjN, j = P
where J,- is the curvature tensor. Introducing the dimension variables
x, p2 c2
Xi E l Kij : RKij R - 1 -rcii = Rt
_ 4Mij Nij PR
IHij -- F/ij -- p-
O'yl 2 fly/ O'yl
then the equilibrium equations become
1 ~2tnij
t- K, jn~j = p
4p 2 c~Xi •Xj
Since m, n, K and X are all of order unity, as p increases, the size of the
bending term is reduced, and hence the pressure tends to the membrane
solution. This also demonstrates that p is the relevant parameter when local
effects predominate.
Limit loads for some defect-free shell structures are shown in Fig. 52.
7.2 Membrane solution for pressure loading
For an axisymmetric closed shell the membrane solution at any point
depends only on the local geometry and is given by
__N~=2sin~b
Pro No= 2 Pro ~b I 2 r° c~1
_
sin r I sm

72. 268 A. G. Miller
e~
Y
-=
o -"
= =
r~
= E c.U
e
u ii • .4: i~ i,
"E I
C u~
U E
.%
.=_
z-:: ..-: :~°o~ o" -"
"J ~a
r_..
L~
~ oo ~ ,,.
r~
br,
o oo_~ ~ ~ ,,
UlVlv

73. Review of limit loads of structures containing defects 269
where 4) is the co-latitude, r o is the circle of latitude radius, r x is the
meridional radius of curvature and
1 dr o
rl------
cos 4, d4,
Hence, for an axisymmetric defect at 4,0 of depth a in a shell of thickness t,
the membrane lower b o u n d to the limit pressure is given by
P = 2ay(t - a) sin 4'0
go
This assumes that the defect is deep enough to determine the limit pressure,
and only applies if this pressure is less than the limit pressure of the defect-
free shell. The value of N0 at the defect does not have to be considered, as it
can be discontinuous.
For meridional cracks, the effect of the defect on the limit pressure is given
by the following constraints:
NO( 4'o) No( 4'o)
t t--a
max []aol, Io'0l, ]a, - a0l } ~< ay for Tresca
where 4'0 is the value of 4' along the defect that gives the lowest limit
pressure.
7.3 Approximate lower bound for part-through defect for pressure loading
If a lower bound limit pressure for a through-thickness defect and the
membrane limit pressure for a defect-free structure, of the same geometry,
are both known, then a lower b o u n d solution for the part-through-thickness
case may be determined. 73-~5 If the solutions are
lower b o u n d Pl[t] membrane Pm[t]
where these refer to the solutions for a shell of thickness t, then a lower
bound for the part-through-thickness case is
P = P,[a] + P m [ t - a]
It may be seen that this is compatible with a statically admissible stress field.
An alternative lower b o u n d approach, due to Goodall (see Millerg), is to
split the structure into the ligament and a through-cracked shell of the
original thickness t. Then a lower bound to the case when the ligament is in
pure tension is given by
P = P,[t] + Pm[t -- a]

74. 270 A. G. Miller
This is larger than the above expression, as
el[t] > Pl[a]
However, bending effects have been ignored, so strictly the result is only valid
for a single ligament position, whereas the first expression is valid for all
ligament positions.
These expressions give the global collapse load and may not be
appropriate (see, for example, Section 8.2.1 on surface axial defects in
cylinders).
7.4 Limit pressure for short through cracks
Goodalt 76 derived an approximate lower bound for the limit pressure of a
through-cracked shell using shallow shell theory, assuming that the
membrane stress state of the uncracked shell is known:
2c = crack length
R t = radius of curvature parallel to crack
R 2 = radius of curvature perpendicular to crack
p = c(R2t)- 1/2
N u = membrane stress produced by pressure P, parallel to crack for crack-
free shell
Then the limit pressure is given by
P = R 2 1 + p2 + R1 cryt/
provided 0 <~NH <<.ayt. For axial defects in cylinders this gives (as in Section
8.1.1)
P _ ayt 1
R l+p 2
For meridional defects in spheres it gives
P _ 2ayt 1
R l+p 2
8 C Y L I N D E R S WITH A X I A L D E F E C T S A N D R E C T A N G U L A R
NOTCHES
Only pressure loading is considered here. Test results for this were reviewed
by Miller. 77 Axial defects theoretically have no effect on the limit moment

75. Review of limit loads of structures containing defects 271
for beam bending of the cylinder with respect to a diametral plane.
Experimentally there is a slight effect,vs Through-wall bending stresses are
not normally considered to contribute to the collapse load.
The recommendation of the empirical Battelle formulae in Sections 8.1
and 8.2 is based upon analysing burst pressure results where no allowance
was made for tearing. Therefore their use to evaluate the yield point load and
L r is an approximation.
8.1 Penetrating axial defects
8.1.1
Kitching eta[. 79 consider rectangular defects both experimentally and
theoretically. The material was mild steel. Their experimental loads were
determined by a deformation criterion, and are adequately explained for
axial defects by a limit pressure given by
P = ayt 1
R l+p 2 p>l
p=ayt I 2 ]
R 1 + ( 1 + 8 p 2 ) ~/2 +Cp p<l
where
c
R = cylinder radius
p = (Rt)l/2
2c = defect length t = cylinder thickness
C=0-12
C is a constant introduced because the experimental failure pressures were
higher than the theoretical pressures. (This might be due partly to the use of
¢zyrather than ~r.) The limit analysis comes from a lower bound solution for
rectangular holes using the two-moment limited interaction yield surface.
For a strict lower bound solution, C should be set equal to zero.
8.1.2
The most commonly used collapse formulation is an empirical expression
due to Kiefner et al. 8° at Battelle. This is based on an adaptation of Folias'
L E F M result:
PR 1 M(p) = (1 + 1"61p2) 12 (Folias sl)
~yt M(p)
or the revised version:
M(p) = (1 + 1"05p2) 1/2 (Folias s2)

76. 272 A. G. Miller
1.0
PR
~t
1 Kiefner
I
1,0 1.10 31.0 4!o
P
Fig. 53. Cylinders with through axial cracks.
There is little to choose between these two in the region of practical interest,
0 < p < 7. In the original Battelle formulation for pipeline steel
ar = ay + 10 ksi - ay + 69 MPa
In an R6 assessment, it is more usual to use
Gf = (% + G,)/2
For the Battelle steels the two definitions agreed within 0.5% to 1% over
most of the range, and the maximum discrepancy was 3.2%.
8.1.3
Ew'ing ~'~ has calculated an upper bound and an approximate lower bound
limit pressure. As R / t ~ ~ , both his solutions tend to 0"82/p, compared with
the Battelle limit of 0.79/p.
8.1.4
Miller 77 has compared the Kitching and Kiefner expressions with
experimental results, and concluded that the Kiefner expression based on
Folias 81 gave better agreement. The different theoretical expressions are
compared in Fig. 53.
8.2 Surface axial defects
The geometry is shown in Fig. 54.
2c = detect length b = ligament thickness
R = cylinder radius q = b/t
t = cylinder thickness

77. Review of limit loads of structures containing defects 273
L. [ _l
I i
2 I t
Fig. 54.
t
Geometry of part-through axial defects in cylinders.
8.2.1
The penetrating crack expressions may be used to give a lower bound
estimate of the global collapse pressure by the method given in Section 7.3:
PR ~_.
i a
-----3 l-
a/t
crrt t (1 + l'61c2/Ra) I/2
Ewing TM showed that this gave higher limit pressures than in Section 8.2.3,
and therefore was non-conservative in general. However, the global collapse
pressure may be used for certain geometries (Section 1.8 or Millerg).
8.2.2
Ewing TM derived an upper bound limit pressure. It is not representable by an
analytic formula, and for short or shallow cracks gives a pressure greater
than that for the uncracked shell.
8.2.3 The most commonly used formula is again an empirical Battelle
result: s°
PR q
~rrt 1 - (1 - q)/M(p)
where M(p) is taken from the through-crack result. This is a local collapse
estimate and is not continuous at q = 0 with the through-crack result.
Therefore leak-before-break and catastrophic failure distinctions may be
made.
In this formulation, for cracks with
1
r/< < 1/2
1 + M(p)
the collapse pressure for the through-cracked cylinder is more than that o f
the surface-cracked cylinder, so the cylinder is stable after ligament failure

78. 274 A. G. Miller
and a 'leak' results. For thicker defects, the through-wall defect is not stable
and a catastrophic 'break' results.
8.2.4
Ruiz 83 gave an approximate expression, but it is not recommended for use,
as it does not agree with other results in various limiting cases.
8.2.5
The above thin shell formulae do not distinguish between internal and
external defects, or between rectangular and semi-elliptical defects. There is
not adequate experimental evidence to judge these effects. Chel184 has
proposed empirical expressions for internal defects:
local ligament failure
PR q M(p,q) [1 + 1.61p2(1 r/)] t/2
O'ft 1 -- (1 -- ~I)/M(p, n)
global membrane failure
PR 1-
=r/+--
aft M(p, O)
8.2.6
The above are concerned with ductile instability at Lr maX.Miller t2 compared
published J calculations with reference stress estimates. He concluded that
the best estimate was given by the global collapse pressure as in Section 8.2.1:
PR a a/t
=1
ayt t (1 + 1.61c2/Ra) 1/2
The number of available results was very small, however.
8.2.7
Miller 7v surveyed test results and concluded that the best estimate for burst
pressure was the Battelle local collapse expression in general:
PR rl
aft = 1 -- (1 -- r/)/[(1 + 1"05p2) 1/2]
As noted above, the global collapse pressure is valid in some circumstances.
8.3 Penetrating and surface rectangular defects
8.3.1
Kitching e t al. 79 derived a lower bound expression based on the two-
m o m e n t limited interaction yield criterion for penetrating defects. It is a
generalization of Section 8.1.1.

79. Review of limit loads of structures containing defects 275
c I~
,&_I- A x i s of
stoi
t
Fig. 55. Geometry of cylinder with part-through thickness rectangular defect.
When A is not small compared with unity, there is no experimental
evidence, but the theoretical limit pressure is given by
P=~{A (1--2p2A)2 (1-2p2A)[(1-2p2A)2+8p2(1--A)]t"2}
4p 2 -t 4p 2 p~< 1
P = ayt 1
R l+p 2 p>~l
where
c
t = cylinder thickness
p =--(Rt)l/2
2c = defect length in axial direction fl = defect half angle
t
R = cylinder radius A=
4R(1 + sec fl)
8.3.2
Kitching and Zarrabi s5 consider surface defects (Fig. 55) which include axial
and circumferential defects as limiting cases. The limit pressure is given by
O'ut
P= --~- p(q, p, qS, A)
where p is shown graphically in Figs 56 and 57. This underestimated the
failure pressure in all tests, sometimes excessively:
c 4R b
p =- (Rt)l/2 A =- t q = -t
2c = defect axial length 4, = half circumferential angle of defect
R = cylinder radius b = ligament thickness
t = cylinder thickness
The most important parameters are p and ~/. For open-ended shells, A and
q5 are only o f minor importance. For closed-ended shells, q~is only important
when q < 0-5, and when q~ is greater than a critical value which depends on q.

80. 276 A. G. Miller
e,l
i
~ ~ ~ ~1 i~l N ~'~1 (" ~ ~ ~ ~.~,
d~ ~ ~ .~ L ~ ~ ~ ~ ~. ~
f'M ~
e~
~o~ i ~ '~ ' ~ ° ~ - ~
~ ~

81. Reriew ~?I:limit loads of structures containing d<~,cts 277
71= 0.9 ~=0.9
1.0 1.0
71-'0.1 71--01
0.90 0.98
0.96 0.96
P p=0.1 tO O=0.1
0.94 /.R o .9~. &R
=20 -- = 2 000
t t
0.92 0.92
0.90 i J 0.90 I J
0 90" q) 190" 0 90 ° ~ Ie0"
(O) (c)
l.O 1. o
1]= 0.9 1]=0.9
o.e 0.8
0.6 0.6
p=10 j:) = I0
P &R P t.R
-20 -i.-=2ooo
o.& t o.&
0,2 0.2
"q = 0.1 a-] -- o . i
1 | i iRi0o
90" ~) ! SO ° 90"
(Io) (d)
Fig. 56. Theoretical limit pressures for cylinders with part-through thickness rectangular
defects (from Kitching and Zarrabi85). Open-ended.
The results were obtained from a lower bound analysis using the two-
m o m e n t limited interaction yield criterion. The experimental results are
shown in Table 13. 86 The material was aluminium.
8.4 Thick cylinders with extended axial defect
Chel156 has proposed expressions for extended defects in thick cylinders,
both in plane strain and in plane stress, with crr increased by 2/,,/3 in Mises
plane strain:
l--a t--a
internal P = Cryr I + a external P = ay - - r i

82. 278 A. G. Miller
"q =o.9 11 = 0 . 9
1.0 1.o
0.8 0.8
0.6 0,6
P p:01 P p=0.1
0.4
~ '=20
0,4
. ooo
0.2 O.Z
45"
1
90 °
L"
(a) Co)
1.0 1.0
11=o9 "/1 =0.9
0.8 0.8
0.6 0.6
p:10 p:lO
P
P
0.4
~ '=20 0.4
"~'~" = 2000
O.Z 0.2
"11=0.1 "TI = 0.I
/,I..~ ° I I .J
90" 45" ~ 90"
(b) (d)
Fig. 57. Closed-ended (from Kitching and ZarrabiSS).
This does not reduce to the uncracked thick wall result in the limit a ~ 0 (e.g.
Hill, s3 p. 268):
P = ayln (rr--°) Tresca (independent of end conditions)
P = ~73 a, In ~
/ /
(to) Mises (closed or plane strain)
The Mises open-ended solution tends to the Tresca solution at small ro/r i and
to the Mises closed solution at large ro/ri:
ro outer radius r~ inner radius
Hill's solution may be used to give an approximate solution for the cracked

83. Review of limit loads of structures containing defects 279
Fig. 58. Geometry of cone with meridional defect.
cylinder by putting r i ---,ri + a for internal defects and ro ~ r o - a for external
defects.
8.5 Application of cylinder results to cones with surface meridionai defect
The geometry is shown in Fig. 58. The membrane solution for pressure
loading is given by Baker et al.: sv
N o= P x c o t ~ Nx = l/2Pxcot~
Hence with the Tresca yield criterion the limit pressure is given by
P = o'y(t - a)-
x m cot
This always gives a lower bound. In the case of short cracks, the stress
gradients are high and the membrane solution becomes very pessimistic.
Locally the cone may be regarded as behaving like a cylinder of the same
local radius. With the substitutions
R=xcot~ 0 " - - 0sin~
and the assumptions that the principal stress directions are the x,O
coordinate directions, and that
~N >>--
N
~x x
then the equilibrium equations become identical to those for a cylinder of
radius R. Although the boundary conditions round the circumference will
not be satisfied as 0 has been rescaled, ifthe plasticity is localized in 0 this will
not matter.

84. 280 A. G. Miller
An approximate argument for the conditions dN/dx >>N/x may be given.
The distance over which the membrane stress resultants vary by a f r a c t i o n f
is given by
L = ~ IN =D:
dN/dx
If L is greater than, say 3c/2, then the membrane
solution will be sensibly
constant over the region of plasticity. Taking x = 2 (the value at the crack
centre) and f = 10%, then the cylinder solution will be a reasonable
approximation if
c 1
2 15
If this condition is not satisfied, then the membrane solution should be used.
8.6 Cylinders with an axial array of through-wall defects
8.6.1
Griffiths ss derived a lower bound limit pressure for a cylinder with a
uniform array o f rectangular holes. This is itself a lower bound to the limit
pressure of a cylinder with a regular array of circular nozzles, claiming no
strength from the nozzles. The method is an extension of that of Kitching et
al. v9 (Section 8.3.2) and uses the two-moment limited interaction yield
surface. The geometry is defined in Fig. 59. Only 5 < R/t < 10 is considered,
g.
~ _2¢_ ~ I
,2d 2d
I (a)
/
(b)
Fig. 59. Geometry of multiple defects. (a) Plan view ofvessel with uniformly pitched defects;
(b) section through vessel.

85. Review of limit loads of structures containing defects 281
The results were reviewed by Proctor: 89
PR c
p =-- tTrt p = (R/t)l/2
t C
A- q-1 the ligament 'efficiency'
4R(1 + see fl) d
F o r i n t e r a c t i n g defects
2A + r/(1 - 4A - - 2p2A) + (2A - - 1)q 2
p=
1 - r/(1 -t- 2p2A) P< 1
p=q p>l
1.0
" 0.9
0.9
---0.8
0.8
Limit p r e s s u r e for
0.7 _ -" ~ isotated defect
( K i t c h i n g et 0t,1970)
0.6
=
in 0.5
--0.4 -.
"~ 0. t,
_.i
L=0.3
0.3
0.2
R
--=5
t
| I j ~ I
0.2 O.& 0.6 (18 1.0
p2
Fig. 60. Limitpressure ~ r i n t e r a c t i n g d e ~ c t s ( ~ o m GfiffithsSS). -,Lowerbound;---,
upper bound.

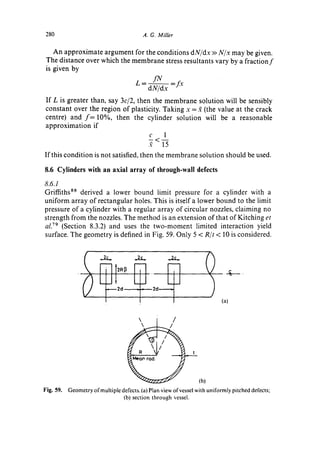
86. 282 A. G. Miller
>,
1.0
0.8
~ d defect
C
q~
0.6 -BS 806 ~ BS5500
E
0 "'-- Limit sotuti¢i~
0.4
¢0
0,2 -
Interocting defects
0 I I I I I
0 0.2 0.4 0.6 0.8 1.0
p~
Fig. 61. Critical ligament efficiencyfor interaction (from GriffithsS%
This is shown in Fig. 60. The critical value of the ligament efficiency below
which the defects interact is given by
1
q¢ = 1 + [2p2(1 - - p l ) ] t/2
wherep~ is the limit pressure of a single defect taken from Section 8.3.2. This
is shown in Fig. 61.
8.6.2
Griffiths 8s gives an upper bound limit pressure for the same problem as
(1 + r/)t
p=q+--
8R
This is compared with the lower bound solution in Fig. 60.
8.6.3
Wilson and Griffiths 9° tested five vessels with multiple defects to check the
applicability of thin shell theory to vessels with 2 < R / t < 5. Provided rt > 0-5,
the lower bound theoretical results were within 10% of the experimental
results.
8.6.4
Kitching et al. 9~ considered a cylinder with two circular holes. When the
holes were arranged circumferentially, they concluded that the limit pressure
was not reduced. When the holes were arranged axially, essentially the same
result as in Section 8.6.1 was derived. They tested 23 mild steel vessels and
showed that the theoretical predictions were conservative.

87. Review of limit loads of structures containing defects 283
2d 2d
V ~- Crack
F,zt. II
Crack
I2ct
I II
2c
1-1 CyLinder a~is
Fig. 62. Schematic geometry of multiple nozzles and associated defects (from Miller92"93).
8.6.5
M i l l e r 92"93 extended the lower bound analysis to include an allowance for
the strength of the nozzles, for the presence of axial cracks touching
alternate nozzles, and for the axial array also being repeated regularly in the
circumferential direction. The geometry is shown in Fig. 62. Because of the
large number of geometrical parameters the results were presented as a
linear programme, with only a sample set of results. The method showed
that the lower bound of Griffiths was slightly overstressed, but only by at
most 5% for the geometries that they considered.
It should be noted that the expressions in Sections 8.6.1-8.6.4 were really
directed at giving lower bound estimates for cylinders with nozzles rather
than cylinders with defects. Also they are based on the analysis due to
Kitching e t aL 79 for single defects, which has been shown to be conservative.
9 CYLINDERS WITH C I R C U M F E R E N T I A L DEFECTS U N D E R
PRESSURE AND BENDING
The loading cases considered here are internal pressure, tension and beam
bending with respect to a diametral plane (see Fig. 63). This type of bending
arises in system stresses in pipework. Through-wall bending stresses are not
normally considered to contribute to the collapse load. Test results for
pressure loading were reviewed by Miller, 77 and for bending and combined
bending and pressure were reviewed by Miller. 94
Notation (see Fig. 63):
M= moment m = M/4R2taf a = defect depth
P= pressure p = PR/2a d q = 1 - a/t
R= radius [3 = c / R
t= thickness : = clrtR
c= defect half length

88. 284 A. G. Miller
F = T t R 2 P
I
M
f
2¢
J
Fig. 63. The circumferential defects are always centred on the peak bending stress in the
situations considered.
Pressure loading is often considered to be equivalent to axial tensile loading,
giving the same end force. The hoop stresses are ignored. This is a valid
approximation for thin shells, but is non-conservative for thick shells.
9.1 Penetrating circumferential defects under bending
9.1.1
The net-section collapse formula was given by Kastner e t al.: 95
m = 4R2tcr r = cos 2
/3 _/3)3
fl--*O m-,l-~- fl-~Tt m-, 1----6-
This is shown in Fig. 64. It is normalized with respect to the plain pipe
collapse moment.
9.1.2
The result given by Kastner e t al. 9 s in Section 9.3.2 may be specialized to
pure bending. It is based on the load to first yield:
M =-l(rr-fl 2sin2fl si2-2/3-
)
l~ R "-t a r 7z 7~ - - fl
fl-,0 m--+~" 1-- fl+= m+--~- 1-
This is shown in Fig. 64.

89. Reciew ~[limit loads O/structures containing dell, ors 285
1.4
"•Net
1.2
- section cotlapse
1.0 ~ , , "~Net - section cottapse w i t h ovat, isation correction
M
~R2to-f ,ira,, o, ,meo to, v=,Oo,,oo
06
06
O.&
0.2
0
I
02
~ I
O.t.
~
0,6
( empirical )
0.8
I
1.0
Fig. 64. Bending moment for cylinders with circumferential through cracks.
9.1.3
Kanninen et aL 96 recommended that for short cracks the limit moment from
Section 9.1.1 should be reduced by multiplying by an ovalization correction
factor, V(/3):
V(/3) = (rt/4)[1 + 0"067(2/3) + 0"000 38(2/3)-' + 0"008 76(2/3)3] /3 ~< 1"17
V(/3 = 1"17)= 1
This is shown in Fig. 64.
9.1.4
An empirical result is given by Wilkowski and Eiber: 9~
M 1
- - = (1 + 0"26.- + 47z 2 - 59z3) - t/2
nR2ta r Mo
The theoretical expression is shown in Fig. 64. The experimental data only
covers up to z = 0"15, and the expression is monotonic only up to z = 0-54. It
is normalized with respect to the bending m o m e n t at first yield for the plain
pipe rather than the limit load.
9.1.5
Miller 94 compared test results and finite-element J calculations with the
above expressions, and concluded that the net-section collapse shown in
Section 9.1.1 gave good agreement, though there was a short crack
ovalization effect in the test results as described in Section 9.1.3. The J
calculations also showed a similar effect, even though they were small
deformation calculations. Further experiments by G r u n m a c h 9a confirm

90. 286 A. G. Miller
213
Fig. 65. Geometry of surface circumferential defects.
that the results in Section 9.1.1 give reasonable agreement for the maximum
moment, when allowance is made for crack growth.
9.2 Surface circumferential defects under bending
The geometry is shown in Fig. 65.
9.2.1
The net-section collapse formula is
n-fl n
m - 4R-~rr = cos - 2 r/<-- or /~<--
fl l+r/
n-fl n
m=4R2tar = r / s i n [ rc - , B2r/ - r / ) ] _ I (1 -r/)sinfl2
M (1 r/>-- or /~>--
l+r/
Different expressions are needed according to whether the neutral axis is in
the flaw or not. If the flaw is in a compressive region, then it might be
assumed that it did not have a weakening effect, and the less pessimistic
uncracked result would be used instead. The expression here reduced to that
given in Section 9.1.1 when r/= 0, to the plain pipe at r/= 1 or/3 = 0, and to the
m e m b r a n e solution f o r / / = n. The plain pipe solution may be obtained by
differentiating the expression for a bar in Section 6.5 with respect to R. The
expression is plotted in Fig. 66.

91. Review of limit loads of structures containing defects 287
t.O
0.8
0.6
r1'i
0.4
0.2
0.2 0.4 0.6 0. a 1.0
Fig. 66. Net-section collapse for surface circumferential defects in bending.
9.2.2
Kastner 9s says that the generalization given in Section 9.1.2 is
unconservative.
9.2.3
An empirical result given by Wilkowski and Eiber 97 using the same
penetrating/surface crack transformation as Kiefner used for axial cracks.
This is a local collapse expression:
M q
M o = from penetrating crack expression
rcR2tar 1 - (1 - tl)/M o
The same comments apply as for the through-crack case.
9.2.4
Willoughby 99 gave an empirical lower bound:
M
~R2ta------~f 1 -- 1.6(1 - t/)fl
=
Experimental verification is limited to q > 0 . 2 . Comparison between
experiment and theory is given in Fig. 67.

92. 288 A. G. Miller
I ! t I i I'
1.2
1,1 D
~a
M 1.0
~rR2t~ 0.9
0x
.
8
0.7
0.6 ~ ~
0.5
I I I I I I
o.~ 0.2 0.3 o.~ o. s 0.6 0,7
(~-q.) 213
Fig. 67. Comparisonbetween failure stress and fl for circumferentialdefectsin pipes under
bending, x, ©, Wilkowski and Eiber;9~ I-I, GIover et al. 1°°
9.2.5
Miller 9" compared test results with the theoretical expressions and
concluded that the net-section collapse given in Section 9.2.1 gave the best
agreement.
9.3 Penetrating circumferential defects under pressure
These are reviewed by Wilkowski and Eiber. ~°1 They conclude that the
crack angle 2fl is a better parameter than the shell parameter p used for axial
defects: p = p(fl).
9.3.1
R a n t a - M a u n u s and Achenbach, L°2 K a n n i n e n et al. ~°a and Schulze et al. 1°4
propose a net-section collapse formula based on a simple stress distribution
analogous to the Tresca plane stress SENT plate case:
p = 1 - fl + 2 sin- 1(sin ill2)
rc
If fl < 50 °, failure due to the hoop stress occurs first, using this model.

93. Review of limit loads of structures containing defects 289
9.3.2
Kastner et al. 95 propose an expression based on an elastic stress distribution
(ignoring stress concentrations or singularities at the defect):
1 ~ { 2sinfl[cos/3+sin/3/(rt-fl)] }
I+
rc --/3 -- 2 sin 2/3/(r~ -/3) -- sin 2/3/2
9.3.3
Eiber et al. ~°5 propose a similar expression but without the enhanced
uniform axial stress term:
1 rc 2 sin fl[cos fl + sin/3/(r~ -/3)]
-=10
p ~ - / 3 rc - fl - 2 sin 2/3/(~ -/3) - sin 2/3/2
9.3.4
Kitching et aL 79 (Section 8.3.2) give a lower bound expression for the limit
pressure for rectangular defects, but in the limit of zero axial extent it is
invalid.
In the short defect limit fl---, 0
p--, 1 ---2fl (Ranta-Maunus and Achenbach; 1°2 Eiber et al. 1°5)
7~
p ~ 1 - 3fl (Kastner et al. 95)
In the long defect limit fl ~ rt
_/3)3
(Ranta-Maunus and Achenbach t°2)
P--' 8rr
-/3)3
(Kastner et aL; 95 Eiber et aL t°5)
P~ 15rc
The 'constraint factors' are less than unity because of the need to carry the
m o m e n t due to the ligament eccentricity.
Sometimes a plastic collapse analysis similar to that in Section 9.3.1 is
done, but the defect is not taken into account when it is a region of
compressive stress. ~°6
The above expressions are compared in Table 14 and Fig. 68.
9.3.5
Miller 77 compared them with experimental results and concluded that the
Kastner expression gave the best agreement, although there were very few
results and these showed a lot of scatter. Miller 94 compared finite-element J
calculations for tensile loading with reference stress predictions based on
net-section collapse and showed that the agreement was reasonable.

94. 290 A. G. Miller
TABLE 14
Comparison of Limit Pressure Solutions for Through Circumferential Cracks
#/~ p #/~ p
Net Kastner Eiber Net Kastner Eiber
section et al. 95 et al. t°5 section et al. 95 et al. 1°5
0-00 I "00 1-00 1'00 0'55 0" 121 0"067 0'073
0"05 0-90 0-85 0"89 0'60 0'085 0"046 0"050
0"10 0"80 0"71 0-77 0"65 0"056 0'030 0-032
0"!5 0"70 0"58 0"65 0-70 0"035 0-018 7 0"020
0"20 0-61 0-47 0-54 0"75 0"020 0"010 6 0-011
0-25 0"52 0"38 0'43 0-80 0"010 0'005 4 0-0055
0-30 0'44 0-30 0'34 0'85 0'004 2 0"0022 0"0023
0"35 0'36 0"23 0'26 0"90 0"001 2 0"0006 0"0006
0-40 0"29 0-174 0-197 0-95 0"0002 0'000 1 0"0001
0"45 0"22 0"130 0-145 1.00 0 0 0
0"50 0'167 0-095 0-105
Therefore the net-section collapse expression given in Section 9.3.1 is
recommended. This approximation ignores the interaction between hoop
stress and axial stress, which is usually conservative. Also these results apply
to any end loading if rcR2p is replaced by the total axial force. The cracks
must always be sufficiently long that the hoop stress does not cause failure.
9.4 Surface circumferential defects under pressure
The relevant parameters are the crack angle 2fl and the fractional ligament
thickness r/ (see Fig. 65). No distinction is made between internal and
external flaws, or with regard to defect shape.
10
on (Acherlbach)
8
6
.4
.2
I I ! I
-2 4 .6 8
Fig. 68. Cylinders with circumferential through cracks.

95. Review of limit loads of structures containing defects 291
9.4.1
Schulze et al. t°4 propose a net-section collapse formula (global collapse):
/3(1 - r/) + 2 sin- t[(1 - q) sin fl/2]
p=l
n
This reduces to the expression given in Section 9.3.1 when ~/= 0 gives the
membrane solution for an axisymmetric defect:
/3== p=q
9.4.2
Kastner et al. 95 propose a formula based on an approximate elastic
distribution (local collapse):
1 7r 2(1 - r/)sin/3 r/[n -/3(1 - r/)]
P 7r_/3(l_n)+r/[rr_/3(l_r/)] or P - =r/ + 2 ( 1 - q) sin /3
This is based on the following assumptions (quoting unpublished work of
Ewing):
(i) The stress could be divided into membrane and bending components.
(ii) The membrane stress was uniform over the cracked cross-section.
(iii) The bending stress was calculable by beam theory applied to the
uncracked cross-section, and over the cracked cross-section
concentrated by dividing by ( 1 - a/t).
(iv) Across the cracked section these assumed stresses are statically
equivalent to the applied load.
Ewing also points out that for large angles the pressure falls below the
membrane value:
p<q for 71-4° < f l < 180 ° or 1.23rad < f l < r r (for all q)
As for the plastic collapse solution
/3== p=q
This expression does not reduce to that given in Section 9.3.2 when q = 0.
Like the Battelle surface crack formulae
q=0 p=0
9.4.3
Chell 8~ has proposed:
(i) Local ligament failure--Battelle transformation on through-crack
plastic collapse:
q
P = 1 - (1 - q)/Mo(fl)

96. 292 A. G. Miller
1.0 I I I
~t%
0.75
t
O.Io- •
o't o-f
a't%
Global
P
tt ( K a s t n e r )
0.5 Membrane
0.25
L I I
L B
I I I I I I
30* 60 * 90 ° 120 ° 150 ° 180 o
Crack half angle p
Fig. 69. Surface circumferential defects under pressure with experimental results from
KWU (Kastner et al.gs). L, Leak; B, break; a/t = 0.75; a * = af/l.2.
where Mo is the through-crack plastic collapse factor, as in Section
9.3.1:
1 /~ + 2 sin- 1(sin/3/2)
p=---1
Mo(fl) x
(ii) Global failure--the plastic collapse load as in Section 9.4.1.
9.4.4
The Schulze et al. 1°4 and Kastner et al. 95 expressions are compared in Table
15 and Fig. 69. Miller 7v compared them with experimental results and
concluded that the Kastner expression gave better agreement, although
evidence was limited. Miller 94 concluded that net-section collapse gave
acceptable agreement for combined pressure and bending.
9.4..5
The above thin shell formulae do not distinguish between internal and
external defects, or between rectangular and semi-elliptical defects.
Intuitively, there seems likely to be less difference between internal and
external circumferential defects than in the axial case. These results apply to
any end loading if g R 2 P is replaced by the total axial force. The crack must

97. Review of limit loads o f structures containing defects 293
TABLEI5
CompafisonofLimitPressureSolutions ~ r S u r h c e C r a c k s
0"1 0"3 0"5 0"7 0"9
G L G L G L G L G L
0"00 1"00 1"00 1"00 1"00 1"00 1"00 1"00 1"00 1"00 1"00
0"05 0-99 0-98 0"97 0"95 0-95 0"89 0"93 0-78 0-91 0"50
0' 10 0"98 0-97 0-94 0-90 0-90 0'79 0"86 0"64 0-82 0"33
0'15 0-97 0"95 0-91 0"85 0"85 0"72 0"79 0"54 0"73 0"24
0"20 0"96 0"94 0'88 0'81 0'81 0"66 0"73 0"46 0"65 0"19
0'25 0"95 0"93 0"86 0'78 0"76 0"60 0"67 0"40 0"57 0-15
0"30 0"94 0'92 0"83 0"75 0-72 0"56 0'61 0"36 0-49 0"13
0"35 0"93 0-91 0'8l 0'72 0"68 0"53 0"55 0-33 0"42 0"11
0.40 0-92 0'90 0"79 0'70 0-65 0-50 0-50 0-30 0-36 0-10
0"45 0-92 0"89 0-77 0'68 0"62 0-48 0'46 0-28 0"30 0"089
0"50 0"91 0"89 0"75 0"67 0-59 0"46 0"42 0"26 0"25 0"082
0'55 0"9l 0-88 0"74 0"66 0-57 0"45 0"39 0"25 0"21 0"076
0"60 0"91 0'88 0'73 0"65 0-55 0"44 0'36 0"24 0'18 0"071
0"65 0"90 0"88 0"72 0"65 0-53 0"43 0"34 0"24 0-15 0'068
0'70 0'90 0"88 0'71 0'65 0-52 0'43 0'33 0'23 0"13 0-066
0"75 0'90 0"88 0'71 0'65 0"51 0"43 0'32 0'23 0-12 0-064
0"80 0-90 0"88 0"70 0"66 0-51 0"44 0"31 0"24 0"11 0-064
0"85 0"90 0"89 0"70 0'66 0"50 0"45 0'30 0'24 0"10 0-065
0"90 0"90 0-89 0"70 0"67 0'50 0"46 0"30 0"25 0'10 0-069
0"95 0-90 0-90 0-70 0"69 0"50 0'48 0'30 0-27 0"10 0-077
1'00 0"90 0'90 0'70 0-70 0'50 0'50 0"30 0"30 0"10 0-10
G, global (= net-section) collapse values of p; L, local (Kastner) collapse values of p; x,
a/t = 1 - rl.
always be sufficiently large that failure is not caused by the hoop stress.
9.4.6
Miller 12 compared published J solutions for this geometry under tension
loading with reference stress estimates. He concluded that net-section
collapse gave better agreement than local collapse estimates did. The
number of available results was limited, however.
9.5 Penetrating circumferential defects under bending and pressure
9.5.1
The net-section collapse formula is given by Kanninen et al.: l°a
m = cos 2

98. 294 A. G. Miller
1.0
o., ~ p= o °
I0 o
p 0.6 - 20 °
0.4~ 30°
02 ~ 40°
o. 0 I I 'k 1 ~ l
0.o 0.2 0.4 0.6 o.8 1.o
m
Fig. 70. Through-wall defect under combined bending and pressure.
This is illustrated in Fig. 70. It reduces to the plain pipe Tresca solution at
/~=0:
Iml= cos(~)
It is a generalization of Sections 9.1.1 and 9.3.1.
Unlike the SENT case in Section 2.4.1, the cracked result cannot be simply
rewritten in terms of the m o m e n t referred to the centre-line, as the geometry
is more complicated.
The sign convention is that m and p are positive when they tend to open
the crack. As in Section 9.2.1, it has been assumed that the defect cannot
withstand a compressive stress. This may be unnecessarily pessimistic.
9.5.2
A lower bound expression is given by Kastner et al.: 95
xPR [x/(x - / 3 ) ] P R 3 sin/~ [cos/3 + sin/~/(~ - 13)] + M
af = (x _/~)2t + [~z - / ~ - 2 sin 2 fl/(n - fl) - sin 2 ~ / 2 ] R ' - t
This is a generalization of the equations in Sections 9.3.2 and 9.1.2, and is
based on load to first yield.
9.5.3
These results apply to any end load if x R ' - P is replaced by the total axial
force. (It is normally pessimistic to ignore the effect of the hoop stress.)
Miller 94 reviewed published test results and concluded that the net-
section collapse results in Section 9.5.1 were in reasonable agreement with
them..
Computations of J for this geometry under combined bending and axial
tension have been carried out by Yang and Palusamy ~°7 and Cardinal et

99. Review of limit loads of structures containing &fects 295
al. l°s Both calculations used versions of A D I N A , modified to calculate J. In
both cases the reference stress derived from the net-section collapse formula
gave better J estimates (though not always conservative) than did the
reference stress derived from Kastner's expression.
Therefore the net-section collapse expression given in Section 9.5.1 is
recommended.
9.6 Surface circumferential defects under bending and pressure
9.6.1
For net-section collapse
(1 - q)/3 + 2 sin - t [m + (1 - q) sin/3/2] 2m
p= 1- sin/3 > -
re l+r/
or
I
m = cos r t p + ( 1 - r/)/31
2
(1 - q)/3
( 1 - ~/) sin/3
2
/3 < r~(1 + p)
- -
l+q
p--1 2qsin-t sin/3 < - -
rt n 2~/ l+q
or
m=qsin rc(l+p)-(l q)fl (1 q)sinfl fl>__
- 1 - n(l + p )
~q " + 2 l+r/
The second pair of expressions apply when the neutral axis is in the defect.
When part of the crack is in compression, it is probably unduly conservative
to neglect its load-carrying capacity.
For proportional loading in P and M, L r has to be determined
numerically. This is a generalization of Sections 9.4.1, 9.2.1 and 9.5.1, when
m, p and q are zero respectively.
9.6.2
Kastner et aL 95 state that the generalization of the result in Section 9.5.2 for
load to first yield is unconservative.
A lower bound expression for the local collapse load is given by Kastner et
a/.: 95
rc 2(1 - r/)sin fl ] m
I= rc--/3(l-r/)~-~/[-~-Z~-I-Z ~]fP-~'TzRZtG-----~f
This is based on an elastic stress distribution, and the limit m o m e n t is
independent of crack size in pure bending. It does not reduce to Kastner's
through-crack result in Section 9.1.2, but it is a generalization of Section
9.4.2.

100. 296 A. G. M i l l e r
9.6.3
Heaton 1°9 gives an approximate expression for an axisymmetric defect,
assuming that the crack has no weakening effect in compressive regions. For
proportional loading
L,=(I r/)p+__ t- -- ~- +
2------~ 4, ~ )
This reduces to the normal expression for pure tension in a cracked cylinder
and for pure bending of an uncracked cylinder.
These results apply to any end load if ~RZP is replaced by the total axial
force. The crack must be large enough so that failure is not caused by the
hoop stress.
9.6.4
Miller 94 reviewed published test results and concluded that they were in
reasonable agreement with the net-section collapse results of Section 9.6.1.
Therefore it is not recommended to use Heaton's expression.
9.7 Thick cylinders with extended circumferential defects under pressure
9.7.1
Chel156 proposed a formula for thick cylinders with axisymmetric defects.
The crack is taken as being pressurized, and the stress is considered as being
as uniform in the ligament. The same formulae apply for both plane strain
and plane stress with ay increased by 2/~/3 for Mises plane strain:
2
F o - -(ri+a)2 (r° - - a)2 - - r2i
internal flaw P = a~ (ri + a) 2 external flaw P = ay r~
ro outer radius ri inner radius
These only apply when the crack is deep enough for the hoop stress not to be
dominant. They are derived from considering the stress distribution in the
plane of the defect only (i.e. net-section collapse).
If the external pressure is not zero, then it is conservative to use the above
formulae with P as the pressure difference. A better lower bound is given by
P,r~ - Por~
CT -~
y 2
r: - 4
where Pi, Po are internal and external pressure, and ri, ro are internal and
external radii of ligament.
This net-section collapse solution is not a complete lower bound solution
as a complete stress field has not been determined. The net-section collapse
approach does give a valid lower bound under axial tensile loading, however.

101. Review o f limit loads o f structures containing defects 297
9.7.2
Ainsworth and Coleman t t o derived a complete lower bound solution for an
axisymmetric external defect, using a Tresca yield criterion:
In( ro ~_<I[i_( ri ~21 P=in(ro)
ro -- a / "~ 2 ro -- a / 3 tr---~y -~t
( r°
In ~
)>~[I--( r or,- a /~21
d
P=ln(ro-a~
tr--~r ri /
+~[1-( r, ')21
ro -- a / I
In the thin shell limit these become the usual formulae:
a 1 P t
t 2 try R
a 1 P 2(t - a)
t 2 trr R
In the shallow crack limit, it reduces to the standard thick cylinder result.
These formulae give lower limit pressures than the net-section collapse
formula, and are to be preferred as having a more accurate derivation.
The deep crack solution is also valid for the Mises yield criterion. The
Mises shallow crack solution will depend on the end conditions (see Section
8.4).
9.8 Thick cylinders with surface circumferential defects under combined
bending and tension
9.8.1
For thick shells with different yield stresses in compression and tension,
Kanninen et aL 96 give the expression derived from net-section collapse:
(1
~_~2 xsin f l ) 2 ( 2 [ - x3 sinfl 1
M =(1 --2() cos~t +--~- m(1 + 2)cos ct-
4ayR2t 2 1 - 2( + 2x( d
where
R = outside radius 2 = ay(compression)/try(tension)
( = t/2R
.v, = a / l
= angle that neutral axis is away from the equator
ct = 2(1 + 2) 1+ + ayRt-(il - O 2(1 + i)
where F = end force.

102. 298 A. G. Miller
For ~ =0, 2 = 1, this reduces to the thin shell expression above that
in Section 9.6.1 for the case where the neutral axis is not in the defect (~ >
~/2 +/~).
9.8.2
The thick shell version of the 'first yield' formula for combined bending and
tension is given by Julisch et al. ~t t On the basis of compatibility with the thin
shell results in Section 9.6, it is recommended to use the net-section collapse
expression given in Section 9.8.1.
10 S P H E R E S
Burst pressure test results for these geometries have been reviewed by
Miller. v7
10.1 Penetrating meridional defects under pressure
Burdekin and Taylor ~2 considered his geometry both experimentally and
theoretically. The material was mild steel. The experimental failure pressures
are adequately explained by a limit pressure expression given by
af2t I (1 +
e =-k--
2
{8p-/icos- 4,)}) + 1
1
¢
R = sphere radius
p -= (Rt)t<2
2c = defect length ~b = half angle subtended by defect
t = sphere thickness
This limit pressure is derived theoretically from the lower bound solution to
the case where the defect has been replaced by a circular hole, with the defect as
a diameter. It is shown in Fig. 71. The two-moment limited interaction yield
surface was used. Burdekin and Taylor's results are also analysed by
Dowling. ~3 R6 Supplement 1 (1979) considered the tests of Lebey and
Roche. ~~4. ~t 5
Miller 77 showed that the Kiefer expression for axial-crack cylinders (see
Section 8.1.2) gave a better (and less conservative) fit to the data. It was
unconservative for all the Lr-dominated Burdekin and Taylor tests using the
Rev. 2 version of R6, but most of this non-conservatism was removed using
the strain hardening version of R6. In terms of the stress intensity factor, or
the elastic stiffness, a meridional crack in a sphere is very similar to an axial
crack in a cylinder, given the same membrane stress and curvature normal to
the crack. Therefore, analogously to the cylinder case, it is recommended to

103. Review of limit loads of structures containing defects 299
10
8
6
4
0 1.'0 2~0 3~0 4'0
P
Fig. 71. Spheres with through meridional cracks.
use the Kiefner expression, adapted to the different plain m e m b r a n e
solution:
PR 1
2o'ft (I + 1"61p2) t/2
10.2 Short surface defects under pressure
10.2.1
Miller tt6 considered this geometry both experimentally and theoretically.
The material was mild steel. For short defects the experimental failure
pressures are adequately explained by a limit pressure expression given by
~rr2t [- 2(1 -- r/) ]
P =--R-- L r/+ (1 + {8p2/(1 - q)}),/2 + 1 .,,.I
c
p =- ( R t ) l / 2 R = sphere radius
r1 - b / t t = sphere thickness
2c = defect length b = ligament thickness
The experiments were done for defects on circles of latitude. The limit
pressure was derived theoretically from a lower b o u n d combination of the
plain m e m b r a n e solution, and a shallow shell approximation to limit
pressure for a through-thickness meridional defect given in Section 10.1. It is
suggested that it may be applied to defects on either great circles or small
circles with the proviso that the small circles must be sufficiently short. In the
absence of evidence, a criterion for small circle defects would be that this
prediction was valid, provided that it was greater than the value given by the
solution for complete small circle defects in Section 10.3.

104. 300 A. G. Miller
10.2.2
An alternative failure expression, which is in equally good agreement with
the test results, is given by the analyses of the Battelle cylinder expression of
Section 8.2.3. It may be regarded as a local collapse expression.
P = ---R-- 1 - (1 - 11)/{(1 + 1"05p2) l/z}
The remarks made about the cylinder analogy in Section 10.1 also apply
here.
10.2.3
Chell a4 has proposed the following expressions:
PR 11
local failure similar to Section 10.2.2
2aft 1 - (1 - 11)/[M(p, x', 4))]
PR (1 -
global failure 2-~r = 11+ M(p, x', 4))
t similar to Section 10.2.1
where
1 "at-[1 "t- {8p2x'/(COS 2 ~)}]1/2 , [1 external defects
M(p, x', 4)) = 2 x = ] a/t internal defects
10.2.4
The expression in Section 10.2.1 is recommended as the global collapse
solution, and that of Section 10.2.2 is recommended as the local collapse
solution. The distinction is discussed in Section 1.8.
Axis of symmetry
N
q
Fig. 72. Geometry for axisymmetric defects in spheres.

105. Review of limit loads of structures containing defects 301
10.3 Part-through-thickness axisymmetric defects under pressure
10.3.1
Goodall and Griffiths t ~7 considered this geometry both experimentally and
theoretically (Fig. 72). The material was mild steel. The experimental failure
pressures are adequately explained by a limit pressure expression given by
a~2t
P= R p(p,q, dp)
where p is shown graphically in Figs 73 and 74:
L
q-- 4~- s i n - '
p ---- (Rt)Z/2 t
L = defect radius b = ligament thickness
R = sphere radius ~b = co-latitude of defect
t = sphere thickness
The limit solution was determined numerically from a lower bound analysis,
using the two-moment limited interaction criterion. A lower bound is always
1.0
0.7 1
~'
-.;,
O J, ~ ' ~ ~" ~'~'
0.3 ~ ~ - - - ~ - ~ . ~
Asymptote as jo ---m--co
i I
1.0 21.0 4.0 ,1.0 ~1.0
P
Fig. 73. Thcorctical limit prcssure for sphere with axlsymmctric defect (Goodal] and
Griffiths ~t ~) (q = 0-3). - - , Crack insidc: - - - , crack outside.

106. 302 A. G. ,Wilier
l.O
L_.. O
:
0.9
0.$
0.7
_--- = u . o a ~x-,, -,~
0.6
0.5
Asymptote osjo --4-- co
b
I I
o!, o.~ o.s ,Io 21o ,.'.o s!o ~'o
P
Fig. 74. Theoretical limit pressure for spher e with axisymmetric defect (Goodall and
Griffiths t t ' ) (q = 0"51. - - - - , Crack inside; - - - , crack outsidc.
given b y p = ~l. For small p the limit pressure is independent o f p and is given
by
p=min {(q I-~ 4tan-'q5 1
At large p
311 + ,72 - 21~7C(I- , l ) ]
p=q+
4p 2
where
. f = l when - i f z +2~r/(1 = g ) > 0 . / ' = ] when - q 2 + 2 ~ r / ( 1 - q ) < 0
Both the small p and large p expressions are the asymptotic forms of the
lower bound expression.
It was found that a u gave better agreement with the experimental results
than did af.
10.3.2
Ewing 44 has shown that the ligament yield criterion for combined shear and
tension used by Goodall and Griffiths ~~v is optimistic by up to 17% and
derived a more refined yield criterion. His results are illustrated in Fig. 75. In
shear one should use true stress-strain relationships in conjunction with an
instability criterion, as necking does not occur. The important thing is
comparison with experiment. A similar objection may be made against the
ligament bending yield criterion used by Goodall and Griffiths, but no
modified version is available.

107. Review ¢~Ilimit loads ¢?lstructures containin¢ dt~/ects 303
1 0.5 O.S
I l j , , , ,
L/R=0.4
l I I l l i , "~
0.5
I I l l I I I I l
0.5 0 O.S
alt
Fig. 75. Comparison of plastic collapse pressures with pressurized hemispherical shells of
various geometries (R/t = 25. various L/R ratios). ----. Rigorous upper bound; , ,
rigorous lower bounds; - - - , limited interaction shallow shell solution; ©, l'-7,experimental
rupture pressures, flow stress correlated; ©, fully circumferential cracks (Goodall and
Griffiths~tV); F-l, part circumferential cracks 132% circumference)(Miller~,6).
(A review o f c o m b i n e d b e n d i n g a n d shear yield criteria is given by
R o b i n s o n ~~a for defect-free shells, but the yield criterion at a c r a c k e d section
will be different.)
II P I P E B E N D S W I T H L O N G I T U D I N A L AND
CIRCUMFERENTIAL DEFECTS
T h e loadings c o n s i d e r e d are internal pressure and in-plane bending. Test
results were reviewed by Miller) t9 T h e r e is little validation, so the results
should be treated with caution.

108. 304 A. G. Milh'r
I
Fig. 76. Loading.
Circumferential
di
thickness(t)
Longitudinaldirection /
Fig. 77. Geometry of smooth pipe bend.
T h e g e o m e t r y is s h o w n in Figs 76 a n d 77.
r = tube radius 2c = defect length
R = bend radius p =- c ( r t ) - 1/2 for longitudinal defects
t = thickness fl = c / r for circumferential defects
). = R t / r 2 gb = angle f r o m c r o w n (see Fig. 76)
M = bending m o m e n t M o = u n c r a c k e d bending m o m e n t
P = internal pressure
11.1 Defect-free bend limit loads
11.1.1
Pr 1 -- r / R
Pressure ( G o o d a l l 120)
2art 1 -- r / 2 R

109. Review of limit loads of structures containing defects 305
0.7
'~" 0.6
¢.,
• 0.5
E
0
E
0.4
0
u
0.3
E o.2
0
Z
0.1
I i I I I
0.0 0.! 02 0.3 0.4 0.5
Bend geometry porometer : k
Fig. 78. Theoretical limit moment of bend with no defects.
This is the asymptotic solution as ).--. 0 for Tresca and limited interaction
yield criteria.
11.1.2
Bending 4r2taf _ 0.94)2/3
Mo (Calladine 12t)
This is also an asymptotic solution, valid for ). <0"5, for the Mises criterion.
The limit moment is shown in Fig. 78.
11.2 Penetrating longitudinal defects under pressure
11.2.1
Defect at crown or extrados. The cylinder solution of Section 8.1 may be
used: ' t 9
Pr 1
art (1 + 1-61p2) z/2

110. 306 A.G. Miller
11.2.2
Defect at intrados:
Pr 1 1 - r/R
(Miller I t 9)
trf-'-t= (1 + 1"61p2) t/2 1 - r/2R
11.3 Penetrating longitudinal defects under bending
For an extended defect at longitude ~b (see Fig. 79)
M = f0"38 + 0"40~;,- t/3 q52- 1/3 < 1"35
0.1<;.<0-5
Mo [0"78 q~2-t/3 > 1"35
I.o
0.| O~
//0/~
m /E
0.6
/
oJ/°
0.4
/t Longitudinal through crack
0.2
1
1 I l
O" 210 * 4 0° 6 0° 810 ° 1 O0°
Crack p o s i t i o n : ~.-_L
Computed tot 0.1~ ~ . < 0 . 5
Fig. 79. Longitudinal through crack: effect on limit load o f pipe bend in bending
(Griffithst 22).

111. Review of limit loads of structures containing defects 307
These formulae are fitted to the numerical results of Griffiths, 122 shown in
Fig. 79. Griffiths used the Tresca yield criterion. Test results show that this
expression is conservative.t t 9
11.4 Surface longitudinal defects under pressure
Defects at the extrados or crown are not affected by the bend curvature, and
the bend may be treated as a cylinder (Section 8.2). F o r defects at the
intrados, the cylinder limit pressure should be reduced by the factor given in
Section 11.0 for the defect-free bend.
11.5 Surface longitudinal defects under bending
There is little evidence on this. What there is indicates that shallow cracks
have little effect, and that linear interpolation in a/t (fractional crack depth)
between 0 and 1 is conservative (see Sections 11.0 and 11.1). Some results
from Griffiths are shown in Fig. 80.
rib,
b
1.0
m
0.5
I !
0.5 l.O
n
Fig. 80. Effect of longitudinal crack penetration on limit moment of pipe bend
(Griffiths 122). Note: These results are independent of 2. q~¢= 0° (worst case).

112. 308 A. G. Miller
I!
~..~ .~ 6
o
e-,
0
"5 _
[ I I 0
,4' o e4 ~
/°
e~
E
~g
u~
/ O
E
0 u E
e-,
o
%
.,
© O
O
ii
E
o
o
/ I I
e~
L5
o
o o
r~

113. Review of limit loads of structures containing defects 309
11.6 Penetrating circumferential defects under pressure
The bend curvature has no effect, and the results from Section 9.3 are
applicable. For all crack locations
Pr
]3<50 ° -.=1
aft
Pr 2 sin - t (sin fl/2) + fl
fl>50 ° =1
2art rc
11.7 Penetrating circumferential defects under bending
The worst location is uncertain. For cracks extending from the crown
towards the extrados, Griffiths '~22 results may be represented by
M 3/~
-- - 1 (see Fig. 81)
Mo 2~
where Mo is the expression for the uncracked bend in Section 11.0. In
general, a lower bound is given by
M (~) sinfl (seeSection9.1)
Mo = cos 2
11.8 Surface circumferential defects under pressure
The pipe bend curvature has no effect on the limit pressure, and the bend
may be regarded as a cylinder (see Section 9.4).
11.9 Surface circumferential defects under bending
There is little evidence on this. What there is indicates that linear inter-
polation between a/t = 0 and a/t = 1 is conservative (see Sections 11.0 and
11.6). This is based on results o f Grifiths, shown in Fig. 82.
12 C Y L I N D E R - C Y L I N D E R INTERSECTION
12.1 Approximations
12.l.l
If the nozzle has been well designed, with suitable reinforcement, the nozzle
should not weaken the structure, and the defect-free structure may be taken

114. 310 ,4. G. Miller
Te
11 -- --
T Nozzle -.- "
¢1
J'
Fig. 83. Geometry of c.vlinder-c~linder intersection.
to be approximately a plain cylinder. This approach was used, for example,
by Milne ~z3 when analysing crotch corner defects.
12.1.2
Alternatively, a conservative estimate may be made by using the detect-free
results, with the thickness reduced to the ligament thickness. Reviews of
limit loads of defect-free nozzles in cylinders are given by Billington et al. ~2"~
for tension and compression, in-plane and out-of-plane bending, and
Robinson 1_,5.126 for internal pressure.
1.0 ,p tt T Rt T
0.9
0.8 1.0
~ . ~ / ! O. 5 O
0.7 _ - 025
0.6 100
1.0
0.5
2 0.50
0."
_ 0.25
0.3
~ ~ } /" 0.50
0.2 0.25
0.1
0 I I i I I I l I 1 J
0 0.1 0.2 0.3 O.t, 0.5 0.6 0.7 0.8 0 9 1 0
"q
Fig. 84. Limit pressure of cylinder-cylinder intersection. R T = 100. (Straight lines have
been drawn between the computed points.)

115. Reriew ~/ limit load~ c~/"structures containing de/ects 311
1.o
do tl T RI T
o.$
!.0
0.8 . 0.7 0.50
~ 0.25
o.?
0.6 1.0
~ ~ 1.4 0.50 50
0.5 0.25
_ ,o
O.t,
2.8 0.50
0.3
0.25
0.2
0.1
0
0.1 O.'Z o,3
' '
0.4 i
05 '
0.6 i
0.7 i
08 i
09 '
1.0
Fig. 85. L i m i t pressure o f cylinder-cylinder intersections. R/T= 50.
12.1.3
A common approximation is to replace the main cylinder by a sphere with
double the radius.
12.2 Limit pressure for cracked geometry
Limit pressure solutions are available for the geometry shown in Fig. 83.
Lower bound thin shell results using an accurate approximation to the
tiT RI T
.t0
1.0
.9 05
0.50
0.25
.8
1.0
.7 !
0.50 25
0.25
P I 1.0
.5
.4
0.50
.3 0.25
.2
.I
0 I I I l | I i l f
.1 .2 .3 .4 .5 .6 .7 •8 .S 10
q
Fig. 86. Limit pressure of cylinder--cylinder intersection. R/T= 25.

116. 312 A. G. Miller
TABLE 16
Limit Pressures of Cylinder-Cylinder Intersections with External Cracks
a w/R a t R p p
p=---- p(q = 0"6) /'St/= I-0)
R t R 7 T (,=0.1) 1,7=0-31
0-5 0-1 0'25 25"0 0'827 0-828 0-835 0"841
I'0 0-2 0"25 25"0 0"516 0"559 0.571 0"584
2"0 0"4 0'25 25"0 0"249 0"283 0'289 0"289
0'5 0. I 0-50 25"0 0.807 a 0.810 ~ 0.824 ~ 0"859
I'0 0'2 0"50 25"0 0"549 0'606 0'629 0"635
2"0 0.4 0"50 25.0 0"284 0-345 0"358 0"355
0"5 0.1 1.00 25'0 0-830 0"856 0-862 0"919
1'0 0-2 1"00 25"0 0"573 0"683 0.747 0-754
2"0 0"4 1'00 25-0 0"341 0"480 0-518 0'526
0"71 0"1 0"25 50"0 0"726 0'749 0.787 0"790
1'41 0"2 0-25 50"0 0"454 0.471 0.487 0.499
2"83 0"4 0"25 50"0 0'224 0-247 0.261 0"268
0-71 0-1 0'50 50"0 0"769 0-789 0-796 0"804
1'41 0"2 0"50 50"0 0'478 0-519 0.542 0"553
2'83 0-4 0"50 50'0 0"258 0"285 0"303 0"316
0"71 0-1 1"00 50-0 0"788 0"806 0'850 0"865
1.41 0"2 1-00 50"0 0-521 0"608 0.664 0"673
2"83 0"4 1-00 50"0 0"302 0.394 0-420 0'439
I 0"1 0'25 100"0 0"653 0-668 0"675 0"697
2 0"2 0-25 100-0 0'359 0-373 0.376 0-381
4 0"4 0'25 100"0 0"194 0-200 0-214 0-227
1 0'1 0"50 100"0 0"661 0-696 0"721 0'736
2 0"2 0"50 100'0 0"395 0.411 0.435 0"442
4 0'4 0-50 100"0 0-208 0.221 0"240 0"259
1 0"1 1.00 100"0 0"688 0-744 0'808 0.814
2 0"2 1"00 100"0 0"423 0.494 0"546 0"563
4 0-4 1"00 100"0 0'266 0-308 0"323 0"343
p = PR/a~T, where P = limit pressure (lower bound).
q = T'/T.
"Better to take value at I/T=O.25.
Mises yield criterion have been calculated numerically by Robinson (pers.
comm.). The method used was that of Meng. ~'" These results are shown in
Tables 16 and 17, and Figs 84-86. The defects have little effect unless they are
very deep (q < 0-3). It makes little difference whether the crack is internal or
external, and the sign of the difference between the two varies with geometry.
Comparison of these results with the axisymmetric approximation of that
in Section 12.1.3 shows that the approximation gives non-conservative
values for the limit pressure.

117. Review o f limit loads o f structures containing defects 313
TABLE 17
Limit Pressures of Cylinder-Cylinder Intersections with Internal Cracks
a t R
-~ -~ p(q =0-1) p(q = 0.3) p(q = 0.6) p(q= 1.0)
2.0 0.4 1.00 25.0 0-329(0-341) 0-481(0-480) 0-519(0"518) 0.526(0"526)
2-83 0-4 0.25 50.0 0-222(0.224) 0-242(0.247) 0-262(0-261) 0.268(0.268)
0"71 0-1 I'00 50-0 0-817(0"788) 0-837(0"806) 0-865(0"850) 0"865(0'865)
p = PR,,'~rrT, where P = limit pressure (lower bound).
q = T'/T.
Values o f p in brackets are for external cracks taken from Table 16.
13 S P H E R E - N O Z Z L E I N T E R S E C T I O N
The geometry considered is shown in Fig. 87. Only radial nozzles are
considered. Theoretical and experimental results have been reviewed by
Miller. 128
13.1 Limit pressure
13.1.1
The results calculated by the most accurate method are those by Lim. t-'9
They were calculated by non-linear optimization of polynomial stress
resultant fields. The yield criterion was that of Ilyushin, as modified by
Axialt h r u s t T
Thickness t i
• j..-Assumed p o s i t i o n of d e f e c t
t h i c k n e s s 1It = b
t
/ P e su e
Thickness J Radius
Fig. 87. Geometry of sphere-cylinder intersection.

118. 314 A. G. Miller
1 !
P P
0.8 0.8
o.6 0.6
0.4 0.4
1.0
0.2 - " " - - - 0 . 1 0 0.2 0.25
0.10
0.0 - - _ , , , ,0.001 O.0 , L , ,
0.00 O.10 0.20 0.30 0.40 0.00 0.10 0.20 0.30 0.40
rlR rlR
RIT =100.0
P '1 • RIT = 50.0 ~1 p I
08 [ 0.8
0.6 0.6
0.4 0.4
O.Z ~ 0 . 1 0 0.2 11"00.25
I I l I
0.( ~ ~ 0.0
0.00 0.10 0.20 0.30 O.LO 0.00 0.10 0.20 0.30 0.40
rlR rlR
Fig. 88. Limit pressure of protruding nozzles, t/T=0"25.
Robinson to allow for shear stresses. The results are shown for a wide range
of geometries in Figs 88-91.
r = nozzle radius t = nozzle thickness
R = sphere radius T = sphere thickness
p = PR/2cyrt t i T = ligament thickness
13.1.2
For geometries not covered by these results, a P P C L I B program may be
used. ~3° This gives four solutions: lower and upper bounds appropriate for

119. Review of limit loads of structures containing defects 315
1
P
I
0.8
P
0.8
0.(
0.6
0.4
o,
~
tOO
0.25
0.2
~ 0 . 1 0
0.2
~ 0 1 0
0.0 . . . . . , i , ,0.001 o.c i i i I
0.00 0.10 0.20 0.30 0.40 0.00 0.10 0.20 0.30 0.40
rlR r/R
1 RIT= 50.0 1
p
0.8 0.8
0.6 0.6
O.t,
0.4 ?oo
-q
0.2 ~ O A O 0.2 ~ . ~ o
o 0.0 , '
0. v . 0 0 0 . '1 0 020
' 0.30
' 0.'t..O 0.00 0.10 0.20 0.30 0.40
rlR r/R
Fig. 89. Limit pressure of protruding nozzles, t/T= 0-50.
small r/R (< 0"3), and lower and upper bounds appropriate for large r/R
(> 0"3). No allowance is made for nozzle yielding. The program gives the
values of the stress resultants at the vessel intersection. These should be
checked against nozzle yielding by the method given in Miller. 129 If the
nozzle yield criterion is violated, then the limit pressure should be reduced by
the appropriate factor.

120. 316 A. G. Miller
1 R/T =25.0 R/T =75.0
P
O.B 0.6 ~
O.G O.G
0.4 0.4
0.2
0.( i t t0001 O.C , i , i
0.00 0.10 0.20 0.30 0.40 0.00 0.10 0.20 0.30 0.40
r/R rlR
t 1 . R/T= 100.
P P
0.8 0.6
O.G 0.6
.q
0.4 0.4
t.00
0,2 0.2 ~ 0 . 1 0
~ 0 . ~ 0
0.0 I i , , 0.0 . . . .
0.00 0.10 0.20 0.30 0.40 0.00 0.10 0.20 0.30 0.40
r/R rlR
Fig. 90. L i m i t pressure o f p r o t r u d i n g nozzles, t,/T= 0.75.
The two solutions have been shown to agree reasonably with each other
and with test results.
13.1.3
Lim's results are for external axisymmetric defects at the intersection, and
with cylindrical nozzles. Miller considers variants on this geometry:
(i) Flush nozzles--these may be considered by PPCL1 B, with allowance
for nozzle yielding as before.

121. Review of limit loads of structures containing defects 317
I ~ RI T =75.0
P
O.B 0.11
0.5
oo O.G
o:,o
O.t. 0.~
0.2 0.t0
0.2
0.0 -,~- • * A°01 O.C ' ' ' '
o.oo O.tO O.ZO 0 . 3 o 0.40 0.00 o.10 020 0 . 3 0 0.~0
rlR r/R
1
RIT=IO0.O
P
0.8 0.8
!
0.6 0.6
0.4 0.t,
0.2 0.2 o12
0.0 t * * i 0.0 * , , ,
0.00 0.10 0.20 0.30 O.t,O 0.00 0.10 O.ZO 0.30 0.t.O
rlR r/R
Fig. 91. Limit pressure of protruding nozzles, t/'T= I'0.
(ii) Finite defect width---this may have a large effect, even for widths less
than the sphere thickness. For large width/thickness ratios, the
results tend to a constant pressure, which may be less than that given
by the sphere membrane solution.
(iii) If the defect radius is greater than the nozzle radius, the effect
depends on the collapse mechanism. For thin ligaments, ligament
yielding dominates and the defect radius controls the limit pressure.

122. 318 A. G. Miller
For thick ligaments, vessel yielding dominates and the nozzle radius
controls the limit pressure.
(iv) The solutions quoted do not allow for the weld profile. The beneficial
effects of the fillets may be allowed for approximately by a method
due to Ewing (given in Miller12S), which gives an effective ligament
thickness for use in the above solutions, calculated in terms of the
fillet weld's geometrical parameters.
(v) Internal defects--these are less deleterious than external defects, the
maximum difference being in the intermediate ligament thickness
r6gime.
(vi) Part-circumference defects--there is only a very small number of test
results available for this and general conclusions cannot be drawn.
(vii) Conical nozzles--these have a higher limit pressure than the
corresponding cylindrical nozzles. The limit pressure is non-zero
even for zero ligament. If frictional effects are included the difference
5
la_
II /"
d
0 0.2 0..' 0.6 08 1 T.2
p =r 14"T~
Fig. 92. L o w e r b o u n d collapse loads, ignoring shear. Mo = err 2 ,'4 collapse m o m e n t o f plain
shell; F o = 2 r i M o = collapse load o f plate under point load; Q, experiment (flow stress
correlated), untracked case.

123. Reriew o/limit hinds O[structures containing dqi~'cts 319
is even greater. Ewing has written a program (PPCL02) which gives
an upper bound.
13.2 Limit thrust
13.2.1
The solutions for this are also calculated by Ewing's program (PPCLIB),
which gives the equivalent four solutions as in Section 13.1.2. For defect-free
vessels the results agree well with test results. This comparison and general
results are shown in Fig. 92.
13.2.2
A bending moment M applied to the nozzle may be allowed for
pessimistically by replacing it by an equivalent thrust Fe:
2M
Fo= r
13.2.3
Combined thrust F and bending moment M may be treated conservatively
by linear addition, i.e.
Ftot~ I = F + F~
13.2.4
Combined pressure and thrust: this case is considered explicitly by PPCL1B.
14 CONCLUSIONS
Limit load solutions have been given for the following structures with
defects (listed by section number):
2. Single-edge notched plates under tension, bending and shear.
3. Internal notches in plates under tension, bending and shear.
4. Double-edge notched plates under tension, bending and shear.
5. Short surface defects in plates under tension and bending.
6. Axisymmetric notches in round bars under tension and torsion.
Chordal cracks in round bars under bending and torsion.
7. General shell structures.
8. Cylinders with surface and penetrating axial defects under pressure.
9. Cylinders with surface and penetrating circumferential defects under
bending and/or pressure.
10. Spheres with short penetrating defects, axisymmetric surface defects
and short surface defects under pressure.

124. 320 .4. G. Milh'r
11. Pipe bends with longitudinal and circumferential, penetrating and
surface defects under in-plane bending or internal pressure.
12. Cylinder-cylinder intersections with a defect at the intersection
under internal pressure.
13. Sphere with a penetrating cylindrical or conical nozzle, with an
axisymmetric surface defect at the intersection, under internal
pressure and axial thrust.
Comparison with experimental results has been made. These solutions
assist in performing two-criteria assessments of structural integrity.
ACKNOWLEDGEMENT
This paper is published with the permission of the Central Electricity
Generating Board.
REFERENCES
1. Milne, I., Ainsworth, R. A., Dowling, A. R. and Stewart, A. T., R H/R6--
Rev. 3, Assessnwnt of the Integrity of Structures Containing Defects. CEGB,
UK, 1986.
2. Ainsworth, R. A., TPRD/B/0175/N83, The Assessment of Defects in Str,wtures
o Strain Harden htg Material, C EG B, U K, 1983.
J"
3. Ainsworth, R. A., Engng Fract. Mech., 19 (1984), 633-42.
4. Ainsworth, R. A. and Goodall, I. W., TPRD/B/0137/N82, Defect Assessments
at Elevated Temperature, CEGB, UK, 1982.
5. Ainsworth, R. A., Chell, G. G., Coleman, M. C., Goodall, I. W., Gooch, D. J.,
Haigh, J. R., Kimmins, S. "I".and Neate, G. J., TPRD/B/0784/R86, Assessment
Proce&trefor Defects in Plant Operating in the Creep Range, CEGB, UK, 1986.
6. ASME, Boiler and Pressure Vessel Code, Section III: N,wlear Power Plant
Components Division 1, 1986.
7. Gerdeen, J. C., WRC Bulletin 254, A Critical Evaluation of Plastic Behaciour
Data and a Unified Definition of Plastic Loads Jbr Pressure Components.
Welding Research Council, New York, 1979.
8. Hodge, P. G., Limit Analysis oJ" Rotationally Symmetric Plates and Shells.
Prentice-Hall, Englewood Cliffs, New Jersey, 1963.
9. Miller, A. G., TPRD/B/0716/N85, Ductile Fracture of Ligaments at Part
Penetration Defects, CEGB, UK, 1985.
10. Ewing, D. J. F., TPRD/L/2692/N84, On the Mode III Faihtre of a Long
Submerged Defect, 1984. (See also Int. J. Pres. Ves. and Piping, 24 (1986),
209-37.)
t 1. Bradford, R., SWR/SSD/0710/N86, Calculation of Fracture Parameters for 3-
Dbnensional Surface Cracks attd A rbitra O' Hardening Behaviour, CEG B, U K,
1986.

125. Review of limit loads of structures containing defects 321
12. Miller, A. G., TPRD/B/0811/R86, J Estimation for Surface Defects, CEGB,
UK, 1986.
13. ASME, Boiler and Pressure Vessel Code, Section XI: Rules for lnservice
Inspection of Nuclear Power Plant Components, Articles IWA-3000, IGA-3000
and IMA-3000, 1986.
14. BS 1980, PD6493, Guidance on Some Methods for the Derivation of Acceptance
Levels for Defects in Fusion Welded Joints, Section 8.2: Defect Dimensions and
Interaction, 1980.
15. Miller, A. G., TPRD/B/0865/R86, Ductile Faihlre of Plates with Multiple
Defects or Multiple Ligaments, CEGB, UK, 1986.
16. Haigh, J. R. and Richards, C. E., RD/L/M461, Yield Point Loads and
Compliance Functions of Fracture Mechanics Specimens, 1974.
17. Willoughby, A. A., A Survey of Plastic Collapse Solutions Used in the Failure
Assessment of Partwall Defects, Welding Institute Report 191/1982, 1982.
18. Ford, H. and Lianis, G., Plastic yielding ofnotched strips under conditions of
plane stress, Zeitschr(ft Angewandte Mathematik Physik, 8 (1957), 360-82.
19. Okamura, H., Kageyama, K. and Takahata, Y., Lower bound solutions and
their application to the collapse load of a cracked member under axial force
and bending moment, A S T M STP 803 Elastic-Plastic Fracture: Second
Symposium, Vol. 2--Fracture Resistance Curves and Engineering Applications
(C. F. Shih and J. P. Gudas, eds), ASTM, Philadelphia, PA, 1983, pp. I1-262-II-
277.
20. Green, A. P., The plastic yielding of notched bars due to bending, Quart. J.
Mech. and Applied Maths, 6 (I 953), 223-39.
21. Ewing, D. J. F., Topics in plane strain plasticit), PhD Thesis, Cambridge
University, 1969.
22. Ewing, D. J. E and Richards, C. E., RD/L/N237, The Yield Pohlt Load~ of
Singly Notched Pin-loaded Tensile Strips, CEGB, UK, 1972.
23. Ewing, D. J. F. and Richards, C. E., The yield point loads of singly notched pin-
loaded tensile strips, J. Mech. Phys. Solids, 22 (1974}, 27-36.
24. Ewing, D. J. F., TPRD/L/2362/N82, Plastic Collapse Loads and Sr Ratios.for
Edge Cracked Phttes under Tension and Bending, CEGB, UK, 1982.
25. Kumar, V., German, M. D. and Shih, C. F., An Enghleering Approach.for
Elastic-Plastic Fracture Analysis, EPRI Report NP-1931, 1981.
26. Rice, J. R., The line spring model for surface flaws, in The Surface Crack:
Physical Prohlems and Computational Solutions (J. L. Swedlow, ed.I, ASME,
New York, 1972, pp. 171-85.
27. Shiratori, M. and Dodd, B., The plane strain general yielding of notched
members due to combined axial force and bending--I: Wedge-shaped notches
with large flank angles, hzt. J. Mech. Sci., 20 (1978), 451-63.
28. Nicholson, R. W. and Paris, P. C., A note concerning analytic expressions for
Rice's upper bound solution for fully plastic edge notched strips, hTt. J. Mech.
Sci., 27 (1985), 481-5.
29. Shiratori, M. and Miyoshi, T., Evaluation of constraint factor and J-integral
for single-edge notched specimen, Vol. 3, h~ternational Congress on Materials
3, Cambridge, 1979, pp. 425-34.
30. Green, A. P., The plastic yielding of shallow notched bars due to bending, J.
Mech. Phys. Solids, 4 (1956), 259-68.
31. Crossley, ~'!. R. and Price, R. H., R D/B/N4588--Rev., Integrity Assessment of
Vessel-Skirt hltersection, CEGB, UK, 1979.
32. Chell, G. G., RD/L/N110, Plastic Collapse Loads for Edge Cracked Plates

126. 322 A. G. Miller
Subjected to Tension and Bend Loading, and their Application to the Failure
Assessment Diagram, CEGB, UK, 1979.
33. Parsons, A. B., SSD/SW/R401, O R A C L E - - A Computer Program for the Life
Assessment of Cracked Structures, CEGB, UK, 1982.
34. Ewing, D. J. E, Calculations on the bending of rigid/plastic notched bars, J.
Mech. Phys. Solids, 16 (1968), 205-13.
35. Dietrich, L. and Szczepinski, W., A note on complete solutions for the plastic
bending of notched bars, J. Mech. Phys. Solids, 17 (1969), 171-6.
36. Shiratori, M. and Dodd, B., Effect of deep wedge-shaped notches of small flank
angle on plastic failure, Int. J. Mech. Sci., 22 (1980), 127-31.
37. Dodd, B. and Shiratori, M., The plane strain general yielding of notched
members due to combined axial force and bending--II: Deep circular notches,
Int. J. Mech. Sci., 20 (1978), 465-74.
38. Shiratori, M. and Dodd, B., The plane strain yielding of single-edge notched
plates d u e t o combined bending and axial force, Res. Mechanica, 4 (1982),
159--74.
39. Shiratori, M. and Dodd, B., The plane strain general yielding of notched
members due to combined axial force and bending--llI: Comparison of
theories with experiment, bit. J. Mech. Sci,, 22 (1980), 431-40.
40. Green, A. P. and Hundy, B. B., Initial plastic yielding in notch bend tests, J.
Mech. Phys. Solids, 4 (1956), 128-44.
41. Matsoukas, G., Cotterell, B. and Mai, Y.-W., Hydrostatic stress and crack
opening displacement in three-point bend specimens with shallow cracks, J.
Mech. Phys. Solids, 34 (1986), 499-510.
42. Green, A. P., J. Mech. Phys. Solids, 3 (1954), 1.
43. Ewing, D. J. F. and Swingier, J. N., TPRD/L 2770.N84, Plastic Yielding of an
Edge Cracked Section in the Presence of Shear, CEGB, UK, 1984.
44. Ewing, D. J. F., TPRD/L/2360/N82, Plastic Yielding under Comhbted Tensile'
Shear Loading, CEGB, UK, 1982.
45. Ewing, D. J. F., TPRD/L/MT0036/M82, Plastic Collapse of a Single-edge
Incl#led Notch Testpiece, CEGB, UK, 1982.
46. Hodge, P. G., Plastic: Anah'sis of Structures, McGraw-Hill, New York, 1959.
47. Harrison, R. P., Loosemore, K., Milne, I. and Dowling, A. R., R/H/R6--
Rev. 2, Assessment o)c the bttegrity of Structures Containhlg Defects, CEGB.
UK, 1980.
48. Goerner, F., Methoden zur Beurteilen des Leck-ror-Bruch Verhaltens t'on
¢h'uckfidzrenden Komponenten, Dr-lng. Dissertation, Karlsruhe University,
1984.
49. Ewing, D. J. F. and Spurr, R. J. D., The yield point loads of symmetrically
notched metal strips, J. Mech. Phys. Solid~, 22 (1974), 37-46. (Also RD/L/
N238.)
50. Ewing, D. J. F. and Hill, R., The plastic constraint of V-notched tension bars, J.
Mech. Phys. Solids. 15 (1967). 115-24.
51. Hill, R., On discontinuous plastic states, with special reference to localised
necking in thin sheets, J. Mech. Phys. Solids, i (1952), 19-30.
52. Ewing, D. J. F., The plastic yielding of V-notched tension bars with circular
roots, J. Mech. Phys. Solids, 16 (1968), 81-98.
53. Hill, R., The Mathematical Theory of PlasticiO', Oxford University Press,
Oxford, 1950, pp. 248-52.

127. Review of limit loads of structures containing defects 323
54. Connors, D. C., TPRD/B/SM/SAM/232/M83, On the Failure of Bars with
Staggered Defects, CEGB, UK, 1983.
55. Milne, I., RD/L/N88/78, Calculating the Defect Tolerance of Ferritic Steel
Structures: A Comparison of the BSI Document 'Draft Standard Rules for the
Derivation of Acceptance Levels for Defects in Fusion Welded Joints" and the
CEGB Procedures 'Assessment of the Integrity of Structures Containing
Defects', CEGB, UK, 1978.
56. Chell, G. G., Elastic-plastic fracture mechanics, in Developments in Fracture
Mechanics--1 (G. G. Chell, ed.), Applied Science Publishers, London, 1979,
pp. 67-105.
57. Mattheck, C., Morawietz, P., Munz, D. and Wolf, B., Ligament yielding of a
plate with semi-elliptical surface cracks under uniform tension, hzt. J. Pres.
Ves. and Piping, 16 (1984), 131-43.
58. Ewing, D. J. F., TPRD/L/MT0127/M83, Stress Intensity Factors for Plates and
Cylinders with Long Part-through Cracks, CEGB, UK, 1983.
59. Miller, A. G., TPRD/B/0341/N83, The Ductile Fracture of Plates under Tension
with Surface Flaws of Various Shapes, CEGB, UK, 1983.
60. Hasegawa, K., Sakata, S., Shimizu, T. and Shida, S., Prediction of fracture
tolerances for stainless steel pipes with circumferential cracks, in Circum-
ferential Cracks in Pressure Vessels and Piping--Vol. 2, Proc. 4th National
Congress on Pressure Vessel and Piping Technology, Portland, Oregon (G. M.
Wilkowski, ed.), ASME, 95, 1983, pp. 65-78.
61. Mattheck, C. and Goerner, F., Leak predictions by use of a generalized
Dugdale model for semi-elliptical surface flaws under tension loading, in Life
Assessment of Dynamically Loaded Materials and Structures, 5th European
Conf. on Fracture, Lisbon, 1984 (L. Faria, ed.), LNETI, Lisbon, 1984,
pp. 631-42.
62. Munz, D., Surface cracks, in Elastic-Plastic Fracture Mechanics. Proc. 4th
Advanced Seminar on Fracture Mechanics, Ispra, 1983 (L. H. Larsson, ed.),
D. Reidel, Dordrecht, 1985, pp. 165-201.
63. Shield, R. T., On the plastic flow ofmetals under conditions of axial symmetry,
Proc. Roy. Soc. A, 233 (1955), 267-86.
64. Levin, E., Indentation pressure of a smooth circular punch, Quart. ,qppl. Math.,
13 (1955), 133-7.
65. Szczepinski, W., Dietrich, L., Drescher, E. and Miastkowski, J., Plastic flow of
axially symmetric notched bars pulled in tension, hzt. J. Solids Structures, 2
(1966), 543-54.
66. Bridgman, P. W., The stress distribution at the neck of a tension specimen,
Trans. Amer. Soc. of Metals, 32 (1944), 553-74.
67. Davidenkov, N. N. and Spiridinova, N. I., Mechanical methods of testing:
Analysis of the state of stress in the neck of a tension test specimen, Proc.
A S T M (1946), pp. 1147-58.
68. Siebel, E., Berichte der Fachauschuesse des Vereins Deutscher Eisenhuetten-
leute, Werkstoffauschuss Bericht Nr 71 (1925).
69. Hoffman, M. and Seeger, T., A generalized method for estimating multi-axial
elastic-plastic notch stresses and strains. Part 2: Application and general
discussion, J. Engineering Materials and Technolog); 107 (1985), 255-60.
70. Walsh, J. B. and Mackenzie, A. C., Elastic-plastic torsion ofa circumferentially
notched bar, J. Mech. Phys. Solids, 7 (1959), 247-57.

128. 324 A. G. Miller
71. Akhurst, K. N. and Ewing, D. J. F., TPRD/L/MT0010/M82, The Failure
Assessment of a Shaft Containing a Chordal Crack, CEGB, UK, 1982.
72. Bicknell, M. B. and Ruiz, C., Pressure Vessel Design and Analysis, Macmillan,
London, 1967.
73. Ewing, D. J. F., TPRD/L/MT0038/82, On the Plastic Limit Analysis of Boiler
Shells, CEGB, UK, 1982.
74. Ewing, D. J. E, TPRD/L/2566/N83, On the Plastic Collapse of a Thin-walled
Pressurised Pipe with an Axial Crack, CEGB, UK, 1983.
75. Miller, A. G., TPRD/B/0093/N82, Review of Limit Loads of Structures
Containing Defects, CEGB, UK, 1982.
76. Goodall, I. W., Some observations on fracture mechanics assessment of
pressure vessel components, in Proc. 3rd bit. Conf. on Numerical Methods in
Fracture, Swansea, 1984 (A. R. Luxmoore and D. R. J. Owen, eds), Pineridge
Press, Swansea, 1984, pp. 275-322.
77. Miller, A. G., TPRD/B/0489/N84, Ret'iew of Test Results for Ductile Failure
Pressure of Cracked Spherical and Cylindrical Pressure Vessels, CEGB, UK,
1984.
78. Darlaston, B. J. L. and Harrison, R. P., The ductile failure ofthin-walled pipes
with defects under combination of internal pressure and bending, in Third
ICPVT, Tokyo, Part IL 1977, pp. 669-76 (or SMiRT IV Paper F8 4).
79. Kitching, R., Davis, J. K. and Gill, S. S., Limit pressures for cylindrical shells
with unreinforced openings of various shapes, J. Mech. Eng. Sci.. 12 (1970).
313-30.
80. Kiefner, J. F., Maxey, W. A., Eiber, R. J. and Duffy, A. R., Failure stress levels of
flaws in pressurised cylinders, in Progress in Flaw Growth and Fracture
Toughness Testing, ASTM STP 536, 1973, pp. 461-81.
81. Folias, E. S., An axial crack in a pressurised cylindrical shell, hit. J. Fract.
Mech., 1 (1965), 104-13.
82. Folias, E. S., On the fracture of nuclear reactor tubes, SMiRT1HLondon, 1975.
Paper C4/5.
83. Ruiz, C., Ductile growth of a longitudinal flaw in a cylindrical shell under
internal pressure, bit. J. Mech. Sci., 20 (1978), 277-81.
84. Chell, G. G., TPRD/L/MT0237/M84, ADISC: A Computer Program for
Assessblg Defects hi Spheres and Cylinders, CEGB, UK, 1984.
85. Kitching, R. and Zarrabi, K., Lower bound to limit pressure for cylindrical
shell with part-through slot, Int. J. Mech. Sci., 23 (1981), 31-48.
86. Kitching, R. and Zarrabi, K., Limit and burst pressure for cylindrical shells
with part-through slots, htt. J. Pres. Ves. and Piping, 10 (1982), 235-70.
87. Baker, E. H., Kovalevsky, L. and Rish, F. L., Structural Anah'sis of Shells,
McGraw-Hill, New York, 1972.
88. Griffiths, J. E., NER/SSD/R440, The Limit Analysis of Header Geometries for
Application in Remanent Creep Life Assessments, CEGB, UK, 1981.
89. Proctor, M. W., NER/SSD/R/0535/84, A Ret'iew of Relevant Literature and a
Proposed Test Programme to Int'estigate the Plastic Collapse of Header
Geometries, CEGB, UK, 1984.
90. Wilson, J. D. and Griffiths, J. E., NER/SSD/R/0529/84, The Plastic Behaviour
of Perforated Thick-walled Cylindrical Pressure Vessels with Interacting
Penetrations, CEGB, UK, 1984.
91. Kitching, R., Akwari, A. O. and Sanderson, N., Limit pressures for cylindrical
shells with two adjacent circular cut-outs, hTt. J. Mech. Sci., 15 (1973), 821-3 I.

129. Review of limit loads of structures containing defects 325
92. Miller, A. G., TPRD/B/0177/N82, Limit Pressure of Cylinder with a Two-
dimensional Array of Nozzles and Associated Defects, CEGB, UK, 1982.
93. Miller, A. G., Limit pressure of cylinder with a two-dimensional array of
nozzles, and associated defects, Int. J. Mech. Sci., 27 (1985), 105-15.
94. Miller, A. G., TPRD/B/0725/N85, The Fracture of Cylinders with Defects under
Bending and Combined Bending and Pressure, CEGB, UK, 1985.
95. Kastner, W., Roehrich, E., Schmitt, W. and Steinbuch, R., Critical crack sizes in
ductile piping, Int. J. Pres. Ves. and Piping, 9 (1981), 197-219.
96. Kanninen, M F., Zahoor, A., Wilkowski, G., Abou-Sayed, I., Marschall, C.,
Broek, D., Sampath, S., Rhee, H. and Ahmad, J., EPRI NP-2347, Vols 1 and 2:
Instability predictions for circumferentially cracked type 304 stainless steel pipes
under dynamic loading, EPRI, USA, 1982.
97. Wilkowski, G. M. and Eiber, R. J., Evaluation of tensile failure of girth weld
repair grooves in pipe subjected to offshore laying stresses, J. Energy Resources
Technology, 103 (1981), 48-55.
98. Grunmach, R., Ausbreitung yon Umfangsrissen in Rohren unter Vierpunkt-
biegebelastung, Dr-lng. Dissertation, Karlsruhe University, 1986.
99. Willoughby, A. A., WI Report 191/1982, A Survey of Plastic Collapse Solutions
used in the Failure Assessment of Partwall Defects, Welding Institute Report,
Cambridge, 1982.
100. Glover, A. G., Coote, R. I. and Pick, R. J., Engineering critical assessment of
pipeline girth welds, in Welding Institute Conf on Fitness-jbr-Purpose, 25-28
November t981, London.
101. Wilkowski, G. M. and Eiber, R. J., Reuiew of Fracture Mechanics Approaches to
D~.,fining Critical Size Girth Weht Discontinuities, WRC Bulletin 239, 1978.
102. Ranta-Maunus, A. K. and Achenbach, J. D., Stability of circumferential
through cracks in ductile pipes, Nuclear Engineering and Design, 60 (1980),
33945.
103. Kanninen, M. F., Broek, D., Marschall, C. W., Rybicki, E. F., Sampath, S. G.,
Simonen, F. A. and Wilkowski, G. M., EPRI NP-192, Mechanical Fracture
Predictions for Sensitized StahTless Steel Piping with Circumferential Cracks,
EPRI, USA, 1976.
104. Schulze, H. D., Togler, G. and Bodmann, E., Fracture mechanics analysis on
the initiation and propagation of circumferential and longitudinal defects in
straight pipes and pipe bends, Nuclear Engineering and Design, 58 (1980),
19-31.
105. Eiber, R. J., Maxey, W. A.I Duffy, A. R. and Atterbury, J. J., Investigation of the
Initiation and Extent of Ductile Pipe Rupture, Battelle Memorial Institute
Report, No. 1908, 1971.
106. Marston, T. U. and Norris, D. M., ASME, Section XI: Proposed acceptance
criteria for circumferential flaws in stainless steel piping, in Proc. Cot!f. Fitness-
for-Purpose Vali~kttion qf Welded Constructions, London, 1981, Paper 40,
1982.
107. Yang, C. Y. and Palusamy, S. S., VCE method of J determination for a
pressurized pipe under bending, J. Pressure Vessel Technology, 105 (1983),
16-22.
108. Cardinal, J. W., Polch, E. Z., Nair, P. K. and Kanninen, M. F., Elastic-plastic
finite-element analysis of a circumferentially cracked pipe, in Proc. CSNI/
NRC Workshop on Ductile Piping Fracture Mechanics, NRC, Washington,
1984.

130. 326 A. G. Miller
109. Heaton. M. D., NWR/SSD 83/0173/N, Assessment q['Standpipes. CEGB, UK.
1984.
110. Ainsworth, R. A. and Coleman, M. C.. TPRD,'B/0846/'R86: Example of an
application of an assessment procedure for defects in plant operating in the
creep range, Fatigue Fracture Of Eng. Mat. Struct., 10 (1987), 129-40.
t 1 I. Julisch, P., Stoppler. W. and Sturm, D., Exclusion of rupture for safety relevant
piping systems by component tests and a simple calculation, SMiRT VIII
Brussels, Paper G3/8, 1985.
112. Burdekin, F. M. and Taylor, T. E., Fracture in spherical pressure vessels, J.
Mech. Eng. Sei., II (1969), 486-97. (Also Taylor, T. E. and Burdekin, F. M..
Unstable Fracture h v the Shear Mode #t Spherical Vessels with Long Flaws.
BWRA, C157/2,'66, 1966.)
113. Dowling, A. R., RD/B/N2796, Faihtre o['Cracked Spherical Vessels: Fracture
Mechanics to Plastic Collapse Transition, CEGB, U K, 1973.
114. kebey, J. and Roche, R., Crack propagation on spherical pressure vessels.
SMiRT I!! Brussels, 1975, Paper G4/4.
I 15. Lebey, J. and Roche, R., Crack propagation and initiation in ductile structures.
in A~h,anees in Research on the Strength aml Fracture of Materials, 4th
International Conference on Fracture ([CF4), Waterloo, Canada, June 1977.
Vol. 3A, pp.47-57 (D. M. R. Taplin, ed.), Pergamon, Oxford, 1978.
116. Miller, A. G., TPRD/B/O278/N83, Ductile Failure Pressure ~[ Spheres with
Part-circumferential Part-thickness Cracks, CEG B, UK, t 983.
117. Goodall, I. W. and Griffiths, J. E., RD/B/5044/N81, On the Limit Amtlvsis ~/
Spherical Pressure Vessels with Fully Cireun!['erential Defects, 1981. (Also hit.
J. Mech. Sei., 24 (1982), 635-45.)
118. Robinson, M., The effect of transverse shear stresses on the yield surface for
thin shells, hit. J. Solids Structures, 9 (1973), 81%28.
119. Miller, A. G., TPRD/B/'0806 R86, The Plastic Coll~q~seo[Cracked Pipe Bends
l#lder Internal Pressure or hl-plane Bending, CEGB, UK, 1986.
120. Goodall, I. W., RD/B/N4360, Lower Bound Lhnit Anah'sis ~( Cur~'ed Tubes
Loaded by Combhled htternal Pressure and In-plane Bending Moment. CEGB.
UK, 1978.
121. Calladine, C. R., Limit analysis of curved tubes, J. Mech. Eng. Sei., 16 (1974).
85-7.
t 22. Griffiths, J. E., RD/B/3694, The Ejfeet of Cracks on the Limit Load of Pipes
under In-plane Berating, CEGB, UK, 1976.
123. Milne, I., Application of the CEGB Procedure to the Analysis of HSST
Intermediate Vessel Tests V5 and V9, Paper 35, in Welding blstitute
Conference, CEGB, UK, 1982.
124. Billington, C. J., Lalani, M. and Tebbett, I, E., OTC 4189: Background to new
formulae for the ultimate limit state of tubular joints, in Off2~hore Technology
Conference, Houston, I (1982), pp. 261-7.
125. Robinson, M., A lower bound to the limit pressure of a flush radial cylindrical
branch in a cylindrical pressure vessel, in Deeelopments in Stress AnaO'sisfor
Pressurised Components (R. W. Nichols, ed.), Applied Science Publishers.
London, 1977 (or SMiRT Ill Paper G1/6).
126. Robinson, M., Lower bound limit pressures for the cylinder-cylinder
intersection--a parametric survey, J. Pressure Vessel Technology, 100 (1978).
65-73.

131. Review of limit loads of structures containing defects 327
127. Meng, Q., Plastic Limit Analysis of Pressure Vessels with Defects, PhD Thesis,
UMIST, 1984.
128. Miller, A. G., TPRD/B/O805/R86, Limit Pressure and Thrust for Spheres with
Radial Nozzles and Associated Defects: Comparison of Theory and Experiment,
CEGB, UK, 1986.
129. Lim, C. S., Plastic Limit Pressures for Pressure Vessels with Defects at
Openings, PhD Thesis, Manchester University, 1986.
130. Ewing, D. J. F., TPRD/L/MT0257/84, PPCLIB: A Program to Calculate
Plastic Collapse Loads for Spherical Shells with Set-through Nozzles having
Axisymmetric Defects, CEGB, UK, 1984.