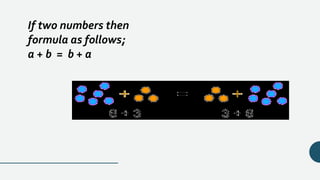
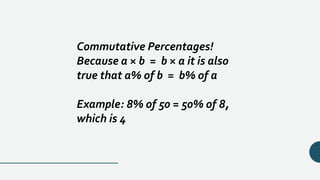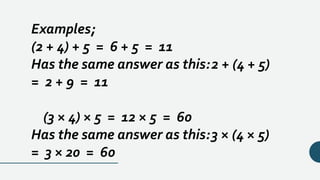The document explains basic mathematical laws, focusing on the commutative and associative properties of addition and multiplication. It states that the order of numbers does not affect the sum or product, providing formulas and examples for clarity. Additionally, it highlights the relationship between percentages and multiplication under the commutative property.

2. BASIC LAWS
OF MATH

3. Commutative Law of Addition;
In this law, order dose not matter
when you add up numbers, you will
always get the same answer.
If we exchange numbers over and over ,get the same
answer
... when we add numbers

4. ANOTHER NAME
this law is also called the Order Property.

5. If two numbers then
formula as follows;
a + b = b + a

6. If three numbers then formula as follows;
x + y + z = z + x + y = y + x + z
using numbers where x = 5, y =
1, and z = 7
5 + 1 + 7 = 13
7 + 5 + 1 = 13
1 + 5 + 7 = 13

7. Commutative Law of Multiplication;
It is an arithmetic law that says it doesn't
matter what order you multiply numbers, you
will always get the same answer. It is very
similar to the commutative addition law.

8. If two terms then the formula as follows;
a × b = b × a
If a=3 and b=5
Then
a × b =15
b × a=15

9. If three terms then formula
as follows;
x * y * z = z * x * y = y * x *
z
where x = 4, y = 3, and z = 6
4 * 3 * 6 = 12 * 6 = 72
6 * 4 * 3 = 24 * 3 = 72
3 * 4 * 6 = 12 * 6 = 72

10. Commutative Percentages!
Because a × b = b × a it is also
true that a% of b = b% of a
Example: 8% of 50 = 50% of 8,
which is 4

11. Associative Law of Addition;
Changing the grouping of numbers that
are added together does not change
their sum.
It doesn't matter how we group the numbers

12. ANOTHER NAME;
This law is also called the Grouping Property.

13. If three terms then formula as
follows;
(a + b) + c = a + (b + c)

14. Associative Law of
Multiplication;
The Associative Law of Multiplication is similar to
the same law for addition. It says that no matter
how you group numbers you are multiplying
together, you will get the same answer.

15. If three terms then formula as follows;
(a × b) × c = a × (b × c)

16. Examples;
(2 + 4) + 5 = 6 + 5 = 11
Has the same answer as this:2 + (4 + 5)
= 2 + 9 = 11
(3 × 4) × 5 = 12 × 5 = 60
Has the same answer as this:3 × (4 × 5)
= 3 × 20 = 60

17. 5 × (2 × 9) is also equal to:
A
5 - (2 - 9)
B
5 × 2 - 9
C
(5 × 2) × 9
D
5 × 11
C correct answer
5 × (2 × 9) = (5 × 2) × 9
(The Associative Law)