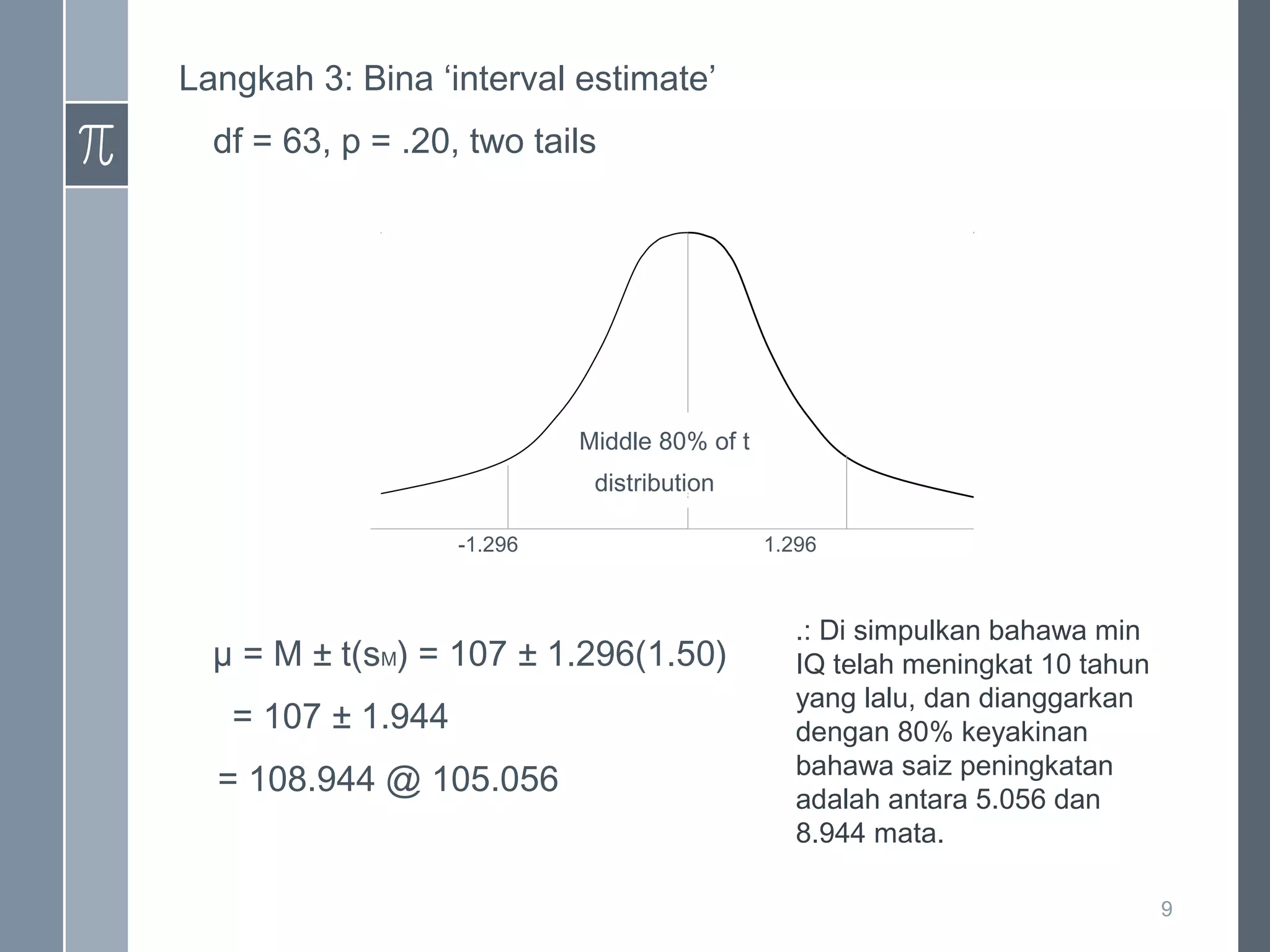
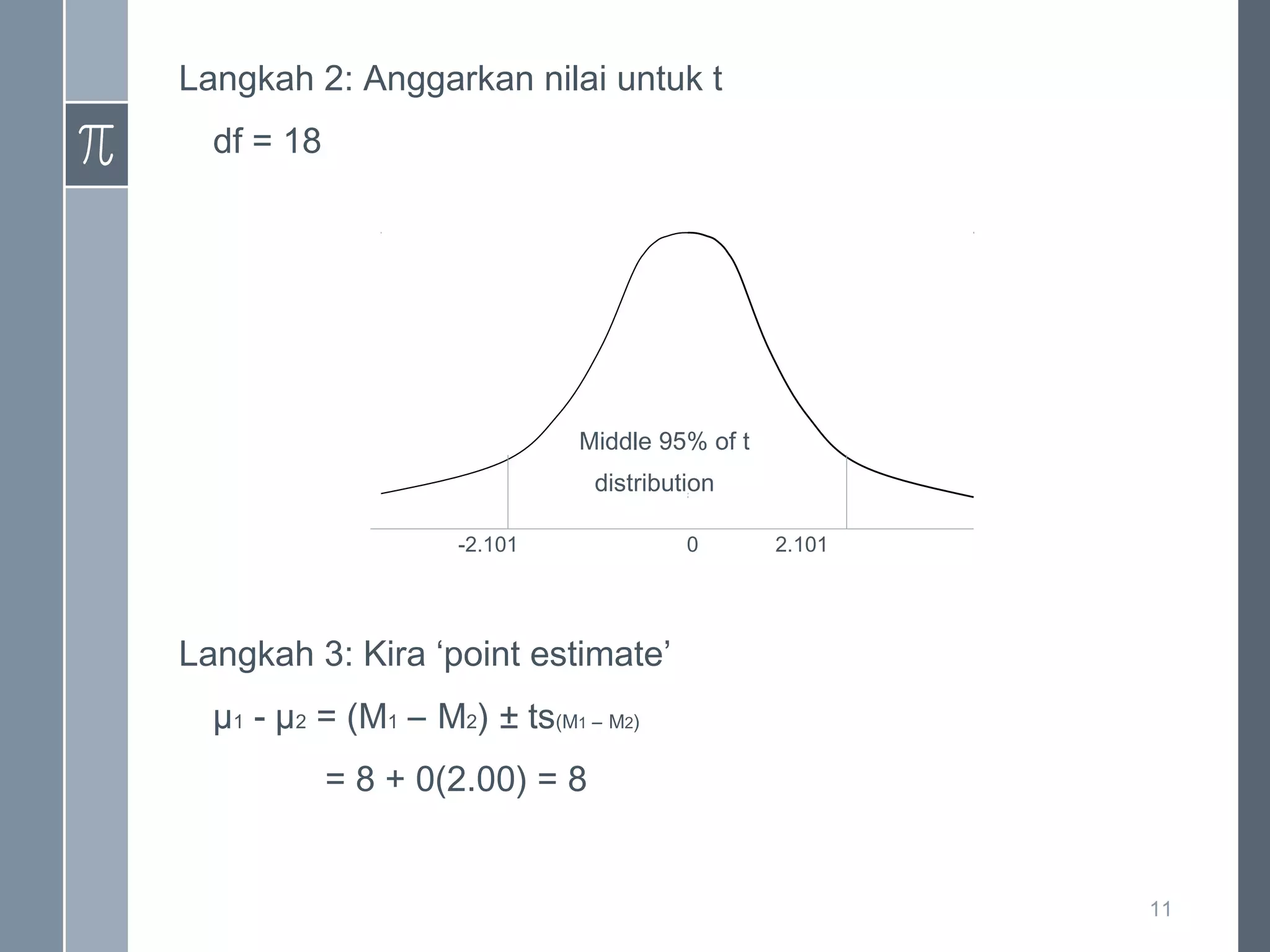
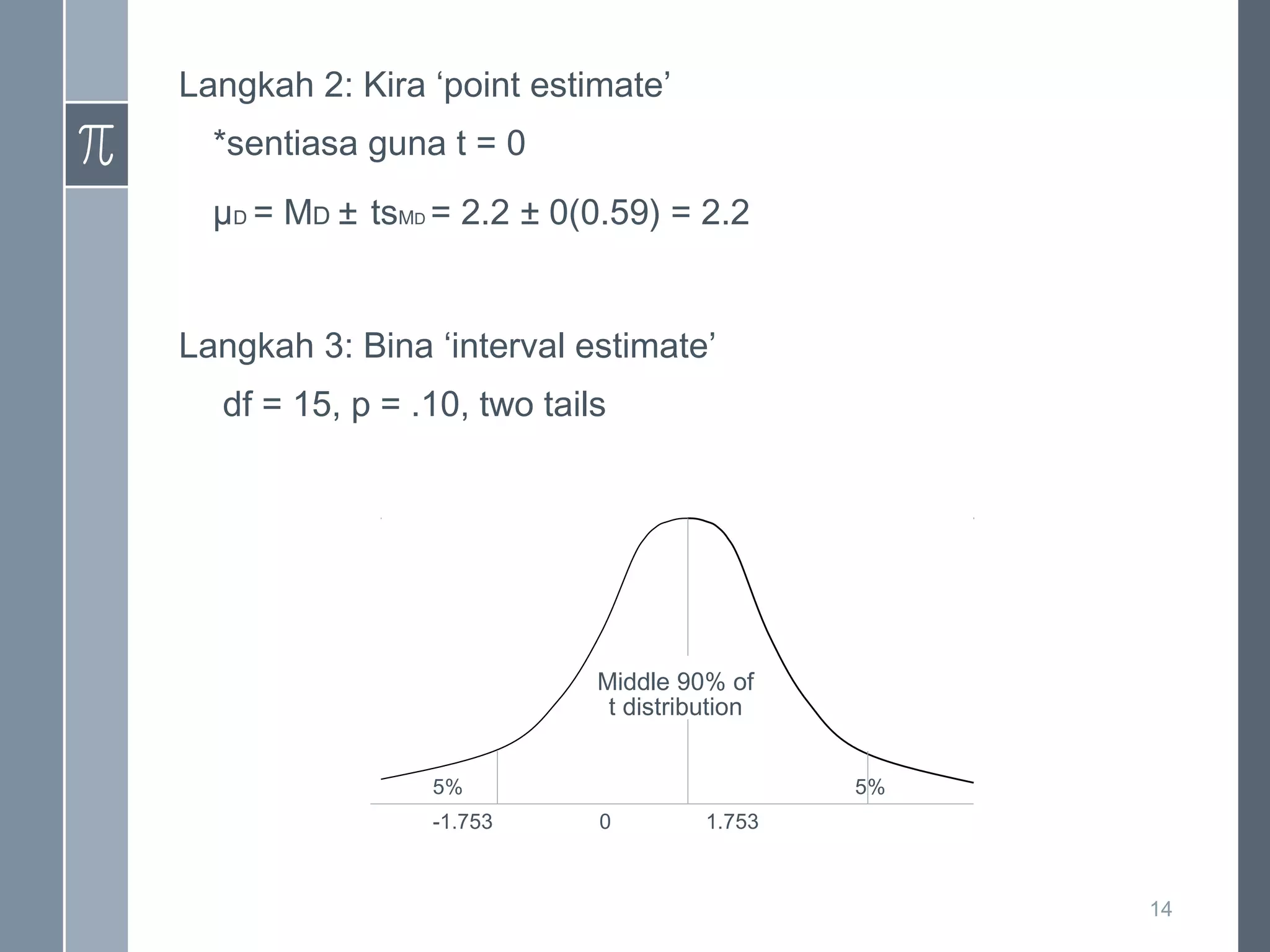
Dokumen ini membahas tentang anggaran statistik, menjelaskan proses anggaran populasi menggunakan sampel, serta perbandingan antara anggaran dan ujian hipotesis. Terdapat tiga situasi di mana anggaran digunakan, dan logik pengiraan termasuk penggunaan rumus t statistik. Kesimpulan menyatakan faktor-faktor yang mempengaruhi lebar selang keyakinan berdasarkan saiz sampel dan peratus keyakinan.

1. BAB 12: ANGGARAN
Disediakan oleh:
Noorhayati Binti Ghazali (GS32743)

2. 12.1ANGGARAN (ESTIMATION)
Maksud: Proses menganggarkan populasi menggunakan
sampel statistik.
Ketepatan Dan Keyakinan Dalam Anggaran
- Dua cara untuk membuat anggaran;
i. Point estimate: menggunakan nombor tunggal sebagai
anggaran terhadap kuantiti yang tidak di ketahui.
ii. Interval estimate: menggunakan julat nombor sebagai
anggaran terhadap kuantiti yang tidak di ketahui. Apabila
anggaran selang (interval estimate) disertai tahap keyakinan,
ia dipanggil selang keyakinan.
2

3. Perbandingan Ujian Hipotesis dan Anggaran
-
Ujian hipotesis dan anggaran adalah sama  keduanya
menggunakan data sampel dan samada z-skor atau t
untuk menjawab soalan tentang populasi yang tidak di
ketahui.
-
Ujian hipotesis akan menentukan samada rawatan itu
mempunyai kesan. Ia akan membezakan antara dua
keputusan, samada;
i.
Tidak. Rawatan tidak meninggalkan kesan (H0)
ii.
Ya. Rawatan tidak meninggalkan kesan (H1).
-
Anggaran adalah untuk menentukan nilai min populasi
tidak diketahui selepas rawatan. Dengan kata lain, ia
menentukan berapa banyak kesan sesuatu rawatan.
3

4. Bila Anggaran Digunakan
- 3 situasi dalam menggunakan anggaran;
i.
Apabila ujian hipotesis H0 ditolak.
ii.
Apabila anda sudah tahu terdapatnya kesan terhadap
rawatan dan ingin mengetahui berapa banyak kesan itu.
iii.
Apabila anda inginkan beberapa maklumat asas
mengenai populasi tidak diketahui.
4

5. Logik Anggaran
- Rumus t statistik yang digunakan untuk ujian hipotesis dan
anggaran ialah;
sample mean
population mean
t = (or mean difference) - (or mean difference)
estimated sample error
or
population mean
(or mean difference)
=
sample mean
± t (estimated standard error)
(or mean difference)
5

6. Ujian Hipotesis
Anggaran
Tujuan: untuk menguji
hipotesis mengenai
parameter yang tidak
diketahui, biasanya nol
hipotesis, yang mana
rawatan tidak memberi
kesan.
Tujuan: untuk
menganggarkan nilai
parameter yang tidak
diketahui.
A. Bermula dengan
menghipotesis nilai untuk
parameter yang tidak
diketahui.
B. Hipotesis digantikan ke
dalam formula dan nilat t
dikira.
C. Jika nilai hipotesis
memberikan hasil yang
munasabah dan gagal
A. Jangan cuba untuk
mengira t statistik.
Sebaliknya, bermula
dengan menganggarkan
nilai t yang sepatutnya.
Strategi ini adalah untuk
memilih yang
munasabah, nilai
kebarangkalian tinggi
untuk t (berdekatan
6

7. munasabah untuk t
(berdekatan zero), kita
menyimpulkan bahawa
hipotesis adalah
munasabah dan gagal
menolak H0. Jika
hasilnya melampau, nilai
kebarangkalian rendah
untuk t, kita menolak H0.
zero). Nilai munasabah
untuk t digantikan ke
dalam formula dan nilai
parameter yang tidak
diketahui dikira.
C. Disebabkan kita
menggunakan nilai yang
munasabah untuk t,
diandaikan bahawa
pengiraan akan
menghasilkan anggaran
populasi yang
munasabah.
Jadual 12.1
7

8. 12.2ANGGARAN DENGAN t
STATISTIK
Anggaran µ untuk ‘Single-Sample Studies’
Contoh:
Rujuk contoh 12.1 ms342
µ = 100, n = 64, M = 107, s = 12
Langkah 1: Kira ‘estimated standard error’
s² = (12) ² = 144
sM = s² = 144 = 12 = 1.50
n
64
8
Langkah 2: Kira ‘point estimate’
µ = M ± tsM
= 107 ± 0(1.50) = 107
8

9. Langkah 3: Bina ‘interval estimate’
df = 63, p = .20, two tails
Middle 80% of t
distribution
-1.296
µ = M ± t(sM) = 107 ± 1.296(1.50)
= 107 ± 1.944
= 108.944 @ 105.056
1.296
.: Di simpulkan bahawa min
IQ telah meningkat 10 tahun
yang lalu, dan dianggarkan
dengan 80% keyakinan
bahawa saiz peningkatan
adalah antara 5.056 dan
8.944 mata.
9

10. Anggaran µ1 - µ2 untuk ‘Independent-Measures Studies’
Contoh:
Rujuk contoh 12.2 ms345
n1 =10, M1 = 93, SS1 = 200
n2 = 10, M2 = 85, SS2 = 160
Langkah 1: Kira ‘standard error’
s²p = SS1 + SS2 = 200 + 160 = 360 = 20
df1 + df2
9+9
18
s(M1 – M2) = s²p + s²p = 20 + 20 = 2 + 2 = 4 = 2.00
n1 n2
10 10
10

11. Langkah 2: Anggarkan nilai untuk t
df = 18
Middle 95% of t
distribution
-2.101
0
2.101
Langkah 3: Kira ‘point estimate’
µ1 - µ2 = (M1 – M2) ± ts(M1 – M2)
= 8 + 0(2.00) = 8
11

12. Langkah 4: Bina ‘interval estimate’
µ1 - µ2 = (M1 – M2) ± ts(M1 – M2) (salah satu hujung selang)
= 8 + 2.101(2.00)
= 8 + 4.202
= 12.202
µ1 - µ2 = (M1 – M2) ± ts(M1 – M2) (satu hujung selang lain)
= 8 - 2.101(2.00)
= 8 - 4.202
= 3.798
.: Di simpulkan bahawa kesan menonton Sesame Street
untuk meningkatkan gred sekolah tinggi, dengan purata
peningkatan adalah antara 3.798 dan 12.202.
12

13. Anggaran µD untuk ‘Repeated-Measures Studies’
Contoh:
Rujuk contoh 12.3 ms 348
n = 16, MD = 2.2, SS = 84
Langkah 1: Kira ‘standard error’
s² = SS = 84 = 5.60
n – 1 15
sMD = s² = 5.60 = 0.35 = 0.59
n
16
13

14. Langkah 2: Kira ‘point estimate’
*sentiasa guna t = 0
µD = MD ± tsMD = 2.2 ± 0(0.59) = 2.2
Langkah 3: Bina ‘interval estimate’
df = 15, p = .10, two tails
Middle 90% of
t distribution
5%
-1.753
5%
0
1.753
14

15. µD = MD – tsMD (salah satu hujung selang)
= 2.2 – 1.753(0.59)
= 2.2 – 1.03
= 1.17
µD = MD – tsMD (satu hujung selang lain)
= 2.2 + 1.753(0.59)
= 2.2 + 1.03
= 3.23
.: Arahan hipnotis akan mengurangkan kesakitan dalam
populasi secara purata 2.2 mata, dan mereka yakin 90%
bahawa penurunan kesakitan adalah antara 1.17 hingga
3.23.
15

16. 12.3KESIMPULAN
Faktor-faktor Yang Mempengaruhi Lebar Selang Keyakinan
- Semakin besar saiz sampel (n), semakin kecil lebar selang
(ketepatan tinggi).
- Semakin tinggi peratus keyakinan, semakin besar lebar
selang (ketepatan rendah).
16