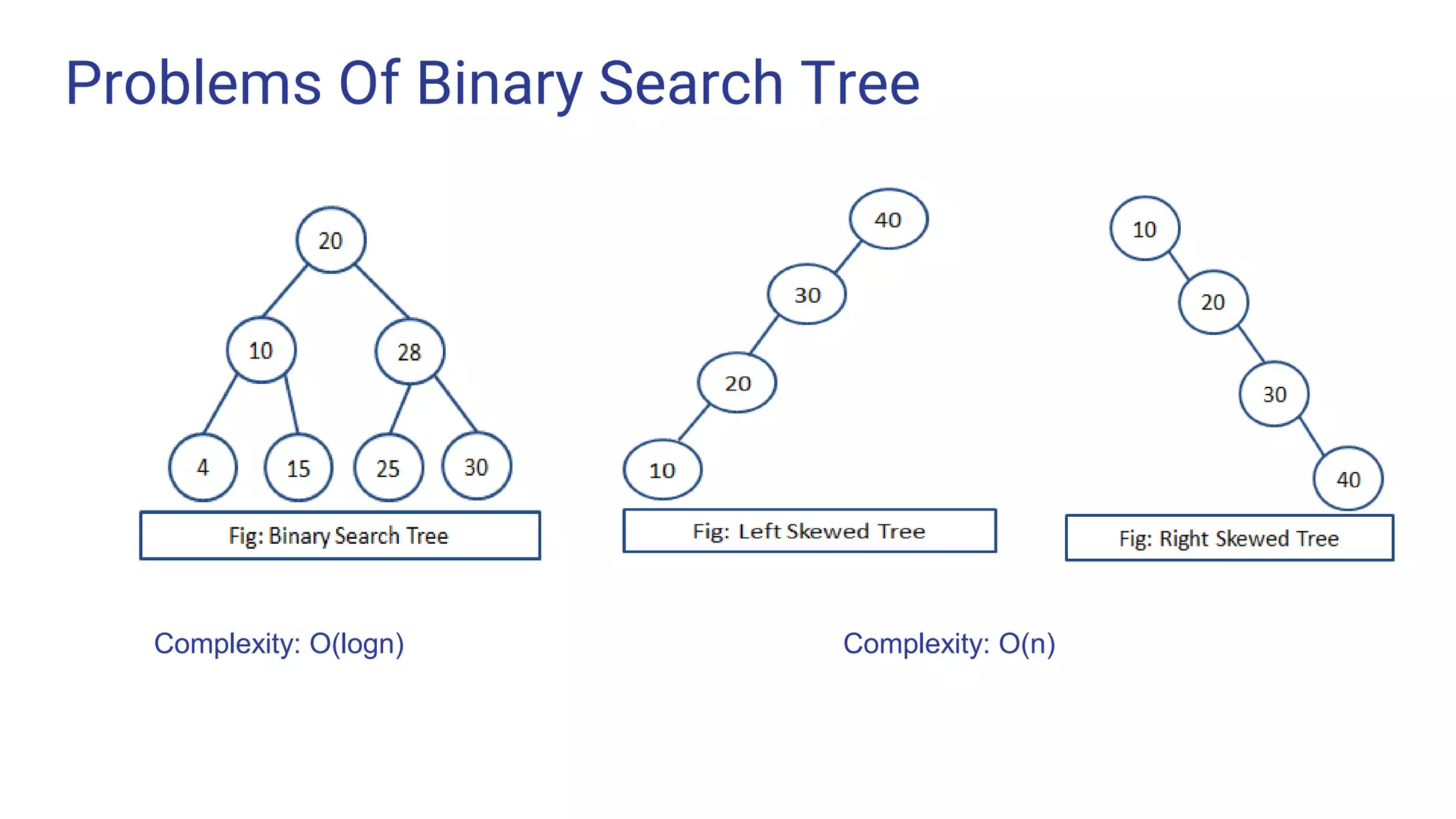
This document discusses AVL trees, which are self-balancing binary search trees where the heights of the left and right subtrees of every node differ by at most one. It covers the definition of AVL trees, problems with regular binary search trees, properties of AVL trees including balance factors, and algorithms for insertion and deletion that rebalance the tree through rotations. The time complexity of operations on an AVL tree is O(log n). Four cases for rebalancing after an insertion are described - left-left, right-right, left-right, and right-left - along with the rotations needed to resolve each case. Deletion is also explained as removing the node and then rebalancing through rotations if needed.

1. AVL Trees
Mohammad Mohsin

2. 1. Definition
2. Problems of Binary Search Tree
3. Properties of AVL Tree
4. Insertion
5. Deletion
Contents

3. ALV Tree
AVL tree is a self-balancing Binary Search Tree(BST) where
the difference between height of left and right subtrees can not
be more than one for all nodes.
The AVL tree is named after its inventors, Georgy
Adelson-Velsky and Evgenii Landis.
Time Complexity: O(log2n).

4. Problems Of Binary Search Tree
Complexity: O(logn) Complexity: O(n)

5. Properties Of AVL Tree
A Binary tree is defined to be an AVL tree if the invariant
Balance Factor(N) ε { -1, 0, +1 }
holds for every node N in the tree where,
Balance factor(N) = Height of the left subtree(N) - Height of right subtree(N)

6. Steps for
Insertion
Let the newly inserted node be w
1. Perform standard Binary
Search Tree(BST) insert for w.
2. Starting from w, travel up and
find the first unbalanced node.
3. Rebalance the tree by
performing appropriate
rotations on the subtree.

7. Cases for Balancing the Tree
Let, z be the first unbalanced node, y be the child of z that comes on the
path from w to z and x is the grandchild of z that comes on the path from
w to z.
Then the following 4 possible arrangements are possible :
a. Left left case: y is the left child of z and x is the left child of y
b. Right right case: y is the right child of z and x is the right child of y.
c. Left right case: y is the left child of z and x is the right child of y.
d. Right left case: y is the right child of z and x is the left child of y

8. Left-Left Case:
(insert 6)
Right-Right Case:
(insert 48)

9. Left-Right Case:
(insert 21)

10. Right-Left Case:
(insert 36)

11. Problems Solution
LL R
RR L
LR LR
RL RL
Case Summarization

12. Deletion in AVL Trees
For deletion in AVL Tree,
1. Perform standard Binary Search Tree(BST) deletion
of the node.
2. Rebalance the tree by left or right rotation

13. Example of Deletion:
(delete 4)

14. Thank You