1. Atomic structure consists of electrons, protons, and neutrons. Rutherford discovered the nucleus through alpha particle scattering experiments. Bohr proposed electrons orbit the nucleus in discrete energy levels. 2. Millikan's oil drop experiment precisely measured the charge of an electron. J.J. Thomson used cathode ray tubes to discover electrons and determine their small mass. 3. Bohr's model of the hydrogen atom explained its stable orbitals and spectral lines by postulating discrete electron energy levels and angular momentum quantization. This resolved issues with Rutherford's model of unstable orbits.

1. 1
Atomic Structure
Content: Evidence for the electrical nature of matter; discharge tube experiments; Thomson’s
atomic model; Rutherford model; Bohr’s model of hydrogen atom; probability picture of
electron; quantum numbers; shapes of s,p,d orbitals; Aufbau and Pauli exclusion principles;
Hund’s rule of maximum multiplicity; electronic configuration of elements; effective nuclear
charge.
Background
Fundamental particles:
 According to Dalton atom is the smallest indivisible particle. But discharge tube
experiments have proved that atom consists of smaller particles.
 In 1897, J.J. Thomson used a cathode ray tube to deduce the presence of a negatively
charged particle: the electron.
 In 1916 Robert Millkan determined the mass of the electron to be 1/1840 the mass of a
hydrogen atom with one unit of negative charge.
 Eugen Goldstein in 1886 observed what is now called the “proton” - particles with a
positive charge, and a relative mass of 1 (or 1840 times greater than that of an electron)
 James Chadwick in 1932 confirmed the existence of the “neutron” – a particle with no
charge, but a mass nearly equal to a proton.
 E. Rutherford through his α-particle scattering proposed that the atom is mostly empty space
and positive charge, and almost all the mass is concentrated in a small area in the center. He
called this a “nucleus”. The nucleus is composed of protons and neutrons (they make the
nucleus!) and the electrons distributed around the nucleus, and occupy most of the volume.
 Electrons, protons and neutrons are the fundamental particles of an atom.
Sub-atomic particles
Fundamental
particle
Charge Mass Specific

2. 2
Charge (e/m)
Electron 1.6022 × 10–19
C, (or) 4.802
× 10–10
e.s.u.
(-1)
9.1095 × 10–31
kg (or)
0.000548 a.m.u.
1/1836 of H atom
1.76×108
c/g
Proton 1.6022 × 10–19
C,
4.802 × 10–10
e.s.u. (+1)
1.67252 × 10–27
kg
(or) 1.007548 a.m.u.
9.58 × 104
c/g
Neutron ‘0’ 1.6749 × 10–27
kg (or)
1.00898 a.m.u.
‘0’
 Every different atom has a characteristic number of protons in the nucleus. Atomic number
(Z) = number of protons.
 Atoms with the same atomic number have the same chemical properties and belong to the
same element.
 Each proton and neutron has a mass of approximately 1 dalton.
 The sum of protons and neutrons is the atom’s atomic mass (A).
 Isotopes – atoms of the same element that have different atomic mass numbers due to
different numbers of neutrons.
Evidence for the electrical nature of matter:
A.Discharge tube experiments:
1. Thomson’s model
Discharge tube consists of glass tube with two metal plates sealed at its two ends and a device
for pumping out the air present in the tube. Thomson studied the deflection of cathode rays under
the influence of magnetic and electrically charged plates and showed that the cathode ray
particles are much lighter than atoms. He also concluded that these negatively charged particles
are present in all kinds of matter, since the nature of radiation did not change with the change in
the material of the cathode or the gas. Apparatus used by J.J Thomson for the study of deflection

3. 3
of cathode rays by electric and magnetic field is shown below. Cathode rays are emitted by the
cathode. These rays move to the right in straight line path, pass through the hole in the anode and
give a narrow beam, which falls on the screen. In a magnetic field this beam is deflected and the
deflection produced by the electric field of suitable strength is applied in the direction at right
angle to the magnetic field applied. The deflection of charge particles is a magnetic field is
directly proportional to its charge and inversely proportional to its mass. The deflection of charge
particles in magnetic field can be reversed by applying the electrostatic field at right angles to the
direction of the magnetic field. Using this idea J.J. Thomson calculated charge to mass (e/m)
ratio of the electrons which was experimentally found to be – 1.76 x 10-11
C kg-1
.
Fig.1: Cathode ray tube
2. Millikan’s Oil Drop Experiment
Millikan’s set up of oil drop experiment is shown in the fig. 2. It consist a chamber maintained
at constant temperature and filled with air at very low pressure. E and E’ are two electrodes. The
space between them is illuminated by light. Tiny oil drops are sprayed by the sprayer A, into the
chamber. As a few droplets pass through the opening O into the space between E and E’, this
inlet is closed. The time taken by the single drop to fall from one fixed point to another under the
action of gravity is noted down with the help of a microscope. The rate of fall is proportional to
its weight. A beam of X-rays is now passed through the window W2 into the air space E and E’.

4. 4
The air gets ionized and the oil globules frequently take up a gas ion and become charged.
Electric field is applied by connecting electrode E’ to the battery,B. The negatively charged
drops experience an upward pull by the positively charged plate is addition to the gravitational
force acting downward. By suitably adjusting the strength of the electric field, the resulting force
can be such that the drop either remains stationary or moves with a constant speed. By measuring
speed charge can be computed. The experiment was repeated by studying the movement of
different size drops. Millikan experiment showed that the charge in each drop was different. The
smallest charge was found to be -1.59 x 10 -19
Coulombs. More accurate methods have led to the
value, e-
= -1.6021 x 10 -19
C.
Fig.2: Millikan’s oil drop apparatus
3. Mass of the electron
The mass of electron varies with its speed. From the value of e-
determined by Millikan and
other (e = -1.6021 x 10-19
C) and the value of e/m at low speed determined by J.J. Thomson. The
mass of the electron at low speed can be calculated as
This is termed as Rest Mass of the electron.

5. 5
4. Rutherford α- particle scattering Experiment
In 1911 Rutherford performed classic experiment for testing the Thomson’s model. He
bombarded thin filaments with high speed α-particles which were obtained from radioactive
polonium. The direction in which α-particle moved was detected with the help of a screen coated
with zinc sulphide. He observed that most of the particles passed through the foil without
deflection and struck the ZnS screen. A few of these were deflected are very large angles from
their original direction and a few were even turned back on their path.
Fig.3: α-particle scattering apparatus
The observations were explained by Rutherford with following assumptions.
1. Atoms have a central nucleus surrounded by electrons.
2. The central nucleus have a positive change which is different is magistrate for different
elements.
3. In neutral atom the number of electrons outside the nucleus equals to the number of positive
charges in the nucleus.
4. Mass of an atom is entirely in the nucleus.
5. The volume of the nucleus is much smaller than the volume of atom of a ratio about 1:1012
.
The stability of the atom is accounted by Rutherford considering that electrons are revolving
around the nucleus is closed orbits. Thus, their centrifugal force balances the force of attraction
and keeps them in their path.
Drawback of Rutherford’s Model
1. Whenever bodies are allowed to fall freely they are accelerated. According to classical
electromagnetic theory an accelerating electrical change must use some of its energy. In other

6. 6
words the orbiting electrons would continuously emit radiation and doing some closer and
closer to the nucleus experiencing more and more electrostatic force and ultimately they will
fall into the nucleus. But this does not happen and atoms are by stable
2. This model could not explain the emission of electromagnetic radiation.
5. Bohr's model
Niels Bohr in 1913 put forward a theory to improve upon the Rutherford’s model of the
structure of atom. His theory was based upon the principles of Max Plank theory of
electromagnetic radiation.
The important postulates of his theory are:
1. The electrons are moving in definite shielded paths called orbits. They can occupy only that
orbit in which the angular momentum of electron is an integral multiple of h/2π or mvr = nh
/2π. This is called Bohr's quantum condition or quantization of angular momentum.
2. Each stationary state corresponds to a definite quantity of energy associated with it. These
are called energy levels. These energy levels are characterized by an integer n, the lowest
level being given number 1. The energy levels corresponding to n=1, 2, 3, 4 are called K, L,
M, N …… shells.
3. The energy level nearer to the nucleus has lower energy while that farthest from it has
maximum energy. When the electron is in the level with lowest energy it is said to be in the
ground state.
4. When electrons absorbs energy in packets or quanta only so that it could move to a higher
energy level. It is said to be in the excited state.
5. When electron jumps back to the ground state, it will release the quantum of energy absorbed.
The released or absorbed energy is equal to the difference between the energies of the two
orbits. If E2 is the energy of the electron in the outer orbit (n2) and E1 is the energy of the
electron in the inner orbit (n1), then E2 – E1 = ΔE = hυ, Where n is called principal quantum
number and it represents the main energy level.
5.1. Bohr's model of H-atom

7. 7
Bohr obtained expression for energy of an electron in hydrogen atom by translating his
postulates into mathematics.
Let ‘r’ be the radius of the orbit in which the electron is resolving and +Ze be the nuclear
charge, where Z is the atomic number. The force of attraction between the electron and nucleus
is given by Coulombs Law.
and
Where ε0 is the permittivity of the free space = 8.854 x 10-12
F/m
The centrifugal force (F1) experience by the electron under the influence of which, the electron
tend to fly away from the nucleus is given by equation.
Equating eq-1 and 2
Incorporating Bohr quantum conditions
, where n= 1, 2, 3,……..
On squaring eq-5
Equating eq-3 and 6
The radius of nth
orbit
a0= 5.29 x 10-11
m – radius of the first Bohr orbit.

8. 8
5.2. Velocity of the electron in the nth
orbit (Vn)
5.3. Energy of an electron
The total energy of electron is sum of potential and kinetic energy,
, where m= mass of electron and v= velocity of electron.
The potential energy of electron at a distance r from the nucleus is given by
Therefore the total energy,
From equation
Substituting eq- 12 in eq-11
The total energy of electron in nth
orbit,
On substitution of the value of r in eq-13 we get
For hydrogen Z=1, the energy will be

9. 9
From eq-16 it is clear that the energy is inversely proportional to the square of n. thus as n
increases, less negative is the energy of the electron in it or the energy of electron has more
positive value.
When the electron is excited from energy level n1 to n2 having energy E1 and E2 respectively, the
energy difference (ΔE) can be calculated as follows,
According to Bohr, the energy of emitted radiation is given by Plank’s Equation,
E= hv
Therefore
And the wavenumber,
The value 1.097 x 107
comes out to be same as Rydberg constant (R). This formula is known as
Ritz Combination Principle. According to which the reciprocal of wavelength of any spectral line
can be expressed as combination of series terms and current terms.
Series in hydrogen spectrum
Name of series n1 (lower orbit) n2 (higher orbit) Spectral region
Lyman series 1 2,3,4,5... ultraviolet
Balmer series 2 3,4,5,6... visible
Paschen series 3 4,5,6,7... near infrared
Brackett series 4 5,6,7... infrared
Pfund series 5 6,7,8... far infrared
5.4. Merits of Bohr's theory

10. 10
 He could explain the spectra of H - atom and other single electron species like He+
, Li2+
etc.
 He could determine frequency, wavelength, wave number of lines in H - spectrum.
 He could calculate the value of Rydberg constant (R).
 He could determine energy and velocity of electron and radius of orbits.
 He could explain the stability of atoms that is why, electrons are not falling into the nucleus
and atoms are not collapsed.
5.5. Demerit's of Bohr's theory
 Bohr failed to explain spectra of multi electron species.
 He failed to explain fine structure of the H-spectrum.
 He failed to consider the wave number of electron.
 Bohr's theory contradicts Heisenberg's uncertainty principle.
 It could not explain the chemical reactivity.
6. Wave nature of electron: de-Broglie theory
de-Broglie proposed that the dual nature is associated with all the particles in motion and they
are called matter waves. Electrons, protons, atoms and molecules, which are treated as particles,
are associated with wave nature. Correlating Planck's equation E = hv and Einstein's equation E
= mc2, we can get wavelength of matter waves.
where λ= wavelength of particle , m = mass of particle, v = velocity of particle.
de-Broglie applied this condition for the material particles in motion. The wavelength of a
particle in motion is inversely proportional to its momentum. Smaller particles with very little
mass have significant wavelength and bigger particles with large mass have negligible
wavelengths. As electron has negligible mass, it has significant wavelength. The wave nature of
electron was proved experimentally by Davisson and Germer in electron diffraction experiments.
Hence electron exhibits both wave nature and particle nature.
7. Heisenberg's uncertainity principle:

11. 11
It is impossible to determine the exact position and velocity of the electron accurately and
simultaneously. If the position is certain, then the accurate determination of velocity is uncertain
and vice-versa, which is called Heisenberg's uncertainity principle.
Where Δx = uncertainity in position, Δp = uncertainity in momentum.
The radius of an atom is of the order of 10–10
m. Hence the uncertainity in the position of
electron cannot be more than 10–10
m. When Δx = 10–10
m. The uncertainity in velocity Δv = 5.8
x 105
m/s. Thus, the minimum uncertainity in its velocity cannot be less than 5.8 × 105
m/s
8. Schrodinger's wave equation
Schrodinger's wave theory is the basis for the modern quantum mechanical model of the
atom. When the exact position of the electron cannot be determined we can predict the
probability of finding the electron around the nucleus. This theory takes two facts into account.
 Wave nature of the electron
 The knowledge about the position of an electron is based on its probability.
 It describes electron as a three dimensional wave in the electric field of positively charged
nucleus.
 Schrodinger's wave equation describes the wave motion of electron along X, Y and Z axes.
In the above equation 'm' is the mass of electron, E is its energy, U is its potential energy, ψ is
called wave function or amplitude of the electronic wave.
The above equation indicates the variation of the value of ψ along x, y and z axes.
9. Probability picture of electron
The square of wave function (ψ2
) is the probability function of the electron and it denotes the
electron cloud density around the nucleus. The region or space around the nucleus where the
probability of finding the electron is maximum (about 95%) is called an atomic orbital. The
probability of finding the electron in the nucleus is zero. The probability of finding the electron
in the radial space around the nucleus is called radial probability. The probability function of

12. 12
electron is called D function. Thus radial probability or electron probability function, D =
4πr2dr.ψ2
. In hydrogen atom the probability of finding the electron is maximum at a distance
0.53 Å from the nucleus. The probability of electron at a distance of 1.3 Å is zero in H-atom. The
plane in which the probability of finding the electron is zero is called node or nodal plane or
nodal surface.
10. Shapes of orbitals
The shape of s-orbital is spherical and spherically symmetrical. It has no nodal planes. The
number of radial nodes for s-orbital = (n – 1).
Fig.4: shape of s-orbitals
The p-orbital has dumb-bell shape. It has one nodal plane. The three p-orbitals are mutually
perpendicular to one another. Each p-orbital has one nodal plane. The lobes are oriented along
the respective axes. For p-orbital, l = 1 m = –1, 0, +1, For px orbital; m = +1, For py orbital; m =
–1, For pz orbital; m = 0;
• px orbital is along the x-axis and its nodal plane is along yz plane.
• py orbital is along the y-axis and its nodal plane is along xz plane.
• pz orbital is along the z-axis and its nodal plane is along xy plane.

13. 13
Fig.5: shape of p-orbitals
The d orbital has 4 lobes and double dumb-bell shape. For d-orbital, l = 2, m = –2, –1, 0, +1, +2,
For dz2
orbital, m = 0, for dxz orbital, m = +1, For dxy orbital, m = –2 for dyz orbital, m = –1,
For dx2
−y2
orbital, m = +2. Each d-orbital has 2 nodal planes.
 dxy orbital is in the xy plane between x and y axes.
 dyz orbital is in the yz plane between y and z axes.
 dxz orbital is in the xz plane between x and z axes.
 dx2
- y2
− orbital is also in the xy plane but the lobes are oriented along x and y axes.
 dz2
orbital is along the z-axis.
 In dxy, dyz, dzx orbitals, the lobes are in between the respective axes. In dx2
−y2
, dz2
orbitals,
the lobes are along the axes. dz2
contains a ring called torus or collar or tyre of negative
charge surrounding the nucleus in the xy plane. It has only 2 big lobes oriented along z-axis.

14. 14
Fig.6: shape of d-orbitals
11. Quantum numbers
To specify the energy and location of electron in an orbit, the following four quantum
numbers are required.
a. Principal quantum number (n)
It is proposed by Bohr and denoted by 'n'. It represents the main energy level. It determines the
size of the orbit and energy of the electron. It takes all positive and integral values from 1 to n.
The maximum number of electrons in a main energy level is 2n2
, and number of orbitals is n2
.
b. Azimuthal quantum number (l)
It is also known as angular momentum quantum number or orbital quantum number (or)
subsidiary quantum number. To express the quantized values of the orbital angular momentum,
azimuthal quantum number was proposed. It is denoted by ‘l’ and takes values from 0 to n – 1.
The number of values of ‘l’ is equal to the value of n. It determines the shape of orbitals. The
number of orbitals in a sub shell is (2 l + 1). The maximum number of electrons in a sub shell is
2(2 l + 1).
 If n = 1, l = 0 (s - sub-shell),

15. 15
 If n = 2, l = 0, 1 (s, p sub-shells),
 If n = 3, l = 0, 1, 2 (s, p, d sub-shells),
 If n = 4, l = 0, 1, 2, 3 (s, p, d, f - sub-shells).
c. Magnetic quantum number (m)
To explain Zeeman and Stark effects Lande proposed magnetic quantum number. It is denoted
by ‘m’. It represents the sub-sub energy level or atomic orbital. It determines the orientation of
orbital in space. When the atom is placed in an external magnetic field, the orbit changes its
orientation. The number of orientations is given by the values of the magnetic quantum number
m. m takes the values form – l to + l through 0. Total values of m for a given value of m = (2 l +
1) values. A sub shell having azimuthal quantum number ℓ, can have (2 l + 1) space orientations.
The number of orbitals in a subshell = (2 l + 1).
d. Spin quantum number (s)
In the fine spectrum of alkali metals pairs of widely separated lines are observed which are
different from duplet, triplet, and quadruplets observed in the hydrogen spectrum. To recognise
and identify these pairs of lines Goudsmit and Uhlenbeck proposed that an electron rotates or
spins about its own axis. This results in the electron having spin angular momentum, which is
also quantised. The electron may spin clockwise or anti clockwise. Therefore, the spin quantum
number takes two values +1/2 and –1/2. Clockwise spin or parallel spin is given +1/2 or ↑ and
anti clockwise or anti parallel spin is given by –1/2 or ↓.
12. Pauli's exclusion principle
No two electrons in the same atom can have the same set of values of all four quantum
numbers. Two electrons in a given orbital have the same values of n, l and m but differ in spin
quantum numbers.
13. Aufbau principle
The orbitals are successively filled in the order of their increasing energy. Among the
available orbitals, the orbitals of lowest energy are filled first. The relative energy of orbital can

16. 16
be known by (n+ℓ) formula. If two orbitals have the same value of (n + ℓ), the orbital having
lower n value is first filled. As atomic number increases, (n + ℓ) formula is not useful to predict
the relative energies of orbitals. For example,
a) up to z = 20, 3d > 4s, Beyond z = 20, energy difference narrows up. Beyond z = 20, 3d < 4s.
b) upto to z = 57,4f > 5p, beyond z = 57, 4f > 5p ; At z = 90, 4f < 5s.
The order of filling of orbitals can be known from Moellar's diagram.
Fig:7. Moellar’s diagram
14. Hund's rule of maximum multiplicity
Orbitals having the same values for n and l are called degenerate orbitals. Pairing of orbitals
will begin after the available degenerate orbitals are half filled. Orbitals with highest resultant
spin value are more stable. The degenerate orbtials are filled to have like spins as far as possible.
15. Electronic configuration of elements
The filling of orbital is governed by Pauli's principle.
The filling of sub-orbit is governed by Hund's rule.
The filling of orbitals of various sub-orbits is governed by Aufbau principle.
The maximum number of electrons that are present in the outer most shell of any atom = 8

17. 17
The maximum number of electrons that are present in the (n–1) most shell of any atom = 18
The maximum number of electrons that are present in the (n–2) most shell of any atom = 32
Electronic configuration of elements
Element At. No Electronic configuration
Hydrogen (H) 1 1s1
Helium (He) 2 1s2
Lithium (Li) 3 1s2
2s1
Beryllium (Be) 4 1s2
2s2
Boron (B) 5 1s2
2s2
2p1
Carbon (C) 6 1s2
2s2
2p2
Nitrogen (N) 7 1s2
2s2
2p3
Oxygen (O) 8 1s2
2s2
2p4
Fluorine (F) 9 1s2
2s2
2p5
Neon (Ne) 10 1s2
2s2
2p6
Sodium (Na) 11 1s2
2s2
2p6
3s1
Magnesium (Mg) 12 1s2
2s2
2p6
3s2
Aluminium (Al) 13 1s2
2s2
2p6
3s2
3p1
Silicon (Si) 14 1s2
2s2
2p6
3s2
3p2
Phosphorus (P) 15 1s2
2s2
2p6
3s2
3p3
Sulphur (S) 16 1s2
2s2
2p6
3s2
3p4
Chlorine (Cl) 17 1s2
2s2
2p6
3s2
3p5
Argon (Ar) 18 1s2
2s2
2p6
3s2
3p6
Potassium (K) 19 1s2
2s2
2p6
3s2
3p6
4s1
Calcium (Ca) 20 1s2
2s2
2p6
3s2
3p6
4s2

18. 18
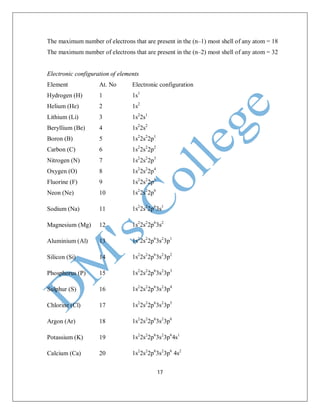
Scandium (Sc) 21 1s2
2s2
2p6
3s2
3p6
4s2
3d1
Titanium (Ti) 22 1s2
2s2
2p6
3s2
3p6
4s2
3d2
Vanadium (V) 23 1s2
2s2
2p6
3s2
3p6
4s2
3d3
Chromium (Cr) 24 1s2
2s2
2p6
3s2
3p6
4s1
3d5
Manganese (Mn) 25 1s2
2s2
2p6
3s2
3p6
4s2
3d5
Iron (Fe) 26 1s2
2s2
2p6
3s2
3p6
4s2
3d6
Cobalt (Co) 27 1s2
2s2
2p6
3s2
3p6
4s2
3d7
Nickel (Ni) 28 1s2
2s2
2p6
3s2
3p6
4s2
3d8
Copper (Cu) 29 1s2
2s2
2p6
3s2
3p6
4s1
3d10
Zinc (Zn) 30 1s2
2s2
2p6
3s2
3p6
4s2
3d10
16. Anomalous electronic configurations
Half filled and completely filled degenerate orbitals give greater stability to atoms. Cr (Z =
24) and Cu (Z = 29) have anomalous electronic configuration due to this reason. Electronic
configuration of Cr atom is 1s2
2s2
2p6
3s2
3p6
3d5
4s1
or [Ar] 3d5
4s1
but not 1s2
2s2
2p6
3s2
3p6
3d4
4s2
.
Electronic configuration of Cu atom is 1s2
2s2
2p6
3s2
3p6
3d10
4s1
or [Ar] 4s1
3d10
but not
1s2
2s2
2p6
3s2
3p6
3d9
4s2
.
17. Magnetic properties
Atoms molecules, ions or any species having unpaired electrons exhibit paramagnetism.
These are attracted into the magnetic field when they are placed in an external magnetic field.
Atoms having the completely paired electrons are repelled by the external magnetic field and are
called diamagnetic.
18. Stability of atoms

19. 19
Theory of exchange forces will explain why Cr has [Ar] 3d5
4s1
but not [Ar] 3d4
4s2
.
According to this theory, greater the number of unpaired electrons, greater is the number of
possible exchange pairs of electrons and more is the exchange energy released and the atom is
more stable. For Cr → [Ar] 3d5
4s1
, the possible number of exchange pairs = 15. If energy
released for each exchange pair is k, the total exchange energy is 15 k. For Cr → [Ar] 3d4
4s2
,
the possible number of exchange pairs = 10 and total exchange energy is only 10k. Therefore Cr
→[Ar] 3d5
4s1
is more stable than Cr(Ar) 3d4
4s2
.
19. Effective nuclear charge concept: The Slater’s Rules
Consider an electron is one of the atomic orbitals of a multi electron atom. Because of the
electrostatic repulsion by the other electrons in the same or other orbitals, the nuclear change felt
by this electron will be less than the actual nuclear charge. This electron is said to be screened
from the influence of the nuclear charge and the reduced charge felt by the electron is known as
the effective nuclear charge.
The effective nuclear charge for any electron in the configuration of an atom may be calculated
with the help of the correlation.
Zeff = Z actual-S
where‘s’ is screening constant / shielding constant.
Screening constant is evaluated by the following empirical rules.
1. The various orbital are grouped as follows and written in the order starting from the side of
the nucleus (1S) (2s3p) (3s3p) (3d) (4s4p) (4d) (4f) (5s5p) etc.
2. For an electron in a group of s,p electrons , the value of screening constant ‘S’ is the sum of
the following contribution.
i. No contribution from any electron present in the groups of orbitals lying on the right side
of the group in which the electron for which S is to be determined is present.
ii. A contribution of 0.35 from every other electron present in the group of orbitals (s,p)
under consideration. A contribution of 0.3 from the electron for which S is to be
calculated belongs to 1s orbital.
iii. A contribution of 0.85 per electron from all electrons with quantum number (n-1)

20. 20
iv. A contribution of 1.0 per electron from all the electrons present in (n-2) th shell and the
next inners hell.
3. For an electron in a group of d or electron rules 2 (i) and 2(iv) are replaced by the rule that
the contribution per electron from all electrons in the inner shell is 1.0
Problem:
1. What is the effective nuclear change felt by 1s electron of the He-atom.
Ans: He-1s2
Screening constant ‘S’ = 1 x 0.3=0.3
Zeff = Zact –S = 2-0.3 = 1.70
2. What is the effective nuclear change felt by a 3d electron of chromium atom?
Ans: Cr- (1s2
) (2s2
p6
) (3s2
3p6
) (3d5
) (4s1
)
No contribution from 4s electron
Zeff = 24-[0.35 x 4) + 1.0 x18) = 4.60
20. Effective nuclear change at the periphery of an Atom or an ion
It is calculated by considering all the electrons present in the electronic configuration of an
atom or the ion.
Problem:
Calculate effective nuclear change at the periphery of nitrogen atom.
Ans.: Zeff at periphery = 7- (5 x 0.35 + 2 x 0.85) = 3.5