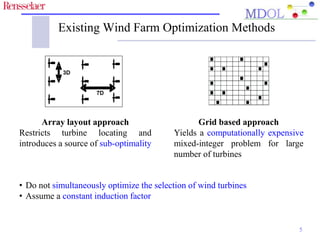
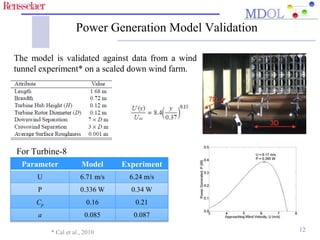
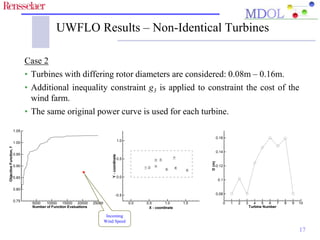
The document discusses optimizing the layout of wind turbines with varying rotor diameters in wind farms to maximize power generation and minimize wake effects. It presents the Unrestricted Wind Farm Layout Optimization (UWFLO) framework, which incorporates an analytical power generation model and utilizes particle swarm optimization. The findings indicate that a flexible turbine arrangement can enhance efficiency significantly compared to traditional layouts.

1. Optimizing the Unrestricted Placement of Turbines of Differing
Rotor Diameters in a Wind Farm for Maximum Power
Generation
Souma Chowdhury*, Achille Messac#, Jie Zhang*, Luciano Castillo*, and
Jose Lebron*
* Rensselaer Polytechnic Institute, Department of Mechanical, Aerospace, and Nuclear Engineering
# Syracuse University, Department of Mechanical and Aerospace Engineering
ASME 2010 International Design Engineering Technical Conferences (IDETC)
and Computers and Information in Engineering Conference (CIE)
August 15-18, 2010
Montreal, Quebec, Canada

2. Presentation Outline
 Motivation and technical background
 Objectives of this paper
 UnrestrictedWind Farm Layout Optimization (UWFLO) framework
 Validation of the power generation model
 Application of UWFLO to experimental scale wind farm design
 Concluding Remarks
2

3. Motivation
 The net power generated by a wind farm is negatively affected by the wake
effects.
 The reduction in the farm efficiency can be offset by optimal planning of the
farm layout.
 A combination of different types of turbines might have the potential to
improve both the power generation capacity and the economy of a wind farm.
www.prairieroots.org 3

4. Wind Farm Optimization
4
• Currently wind energy contributes 2% of worldwide electricity consumption.
• Planned increase in USA by 2030 – 10 fold.
• Advancing wind energy would require optimal wind farm design strategies.
Wake effects lead to significant losses in the
energy available from wind. The
corresponding critical aspects in optimal
wind farm design are (not limited to)
 Farm layout
 Types of turbines to be installed
www.wind-watch.org

5. Existing Wind Farm Optimization Methods
5
Grid based approach
Yields a computationally expensive
mixed-integer problem for large
number of turbines
Array layout approach
Restricts turbine locating and
introduces a source of sub-optimality
• Do not simultaneously optimize the selection of wind turbines
• Assume a constant induction factor

6. Research Objectives
• Develop an analytical wind farm model, which avoids conventional
restrictions in layout planning.
• Develop a robust wind farm optimization framework using the power
generation model, a cost model, and the Particle Swarm Optimization
(PSO) algorithm.
• Investigate the potential of using a combination of different types of
turbines within the scope of layout optimization.
6

7. Basic Components of the UWFLO Framework
Power Generation Model
 Develops a turbine influence matrix based on the wake effects
 Considers a variable induction factor and partial wake-rotor overlap
 Determines the net power generated by the wind farm
Optimization Framework
 Implements a wind farm cost model
 Simultaneously optimizes the selection of differing types of turbines
 Maximizes the net power generation using the PSO algorithm
7

8. UWFLO Power Generation Model
• The flow pattern inside a wind farm is complex, primarily due to the wake
effects and the highly turbulent flow.
• Rotor averaged velocity is determined from the flow profile*
• Step 1
Transformed co-ordinates are evaluated
based on wind direction
8
x X
y Y
   cos   sin

  
      
   sin  cos

  
i i
i i
* Cal et al., 2010

9. Mutual Influence of Turbines
• Step 2
An influence matrix is defined as
where Turbine-i influences Turbine-j if
• Step 3
 

j wake ij
The turbines are ranked in the increasing order of their x-coordinate. Power
generated by turbines is calculated in the increasing order of their rank.
9
1 if Turbine- influences Turbine-
1 if Turbine- influences Turbine-
0 if there is no mutual influence
ij
i j
M j i
 


, 0 &
2 2
ij ij
D D
x  y  

10. • Step 4
Power Generated by the Wind Farm
Effective velocity of wind approaching Turbine-j:*
The power generated by turbine-j:
• Step 5
Coefficient of power
Power generated by the farm: Farm Efficiency:
Power generated by
a standalone turbine
* Katic et al., 1986 10

11. Wake Model
UWFLO uses Frandsen’s wake model*, which calculates the diameter of the
growing wake and the wake velocity as:
Wake spreading constant
However, UWFLO has the flexibility to use any standard wake model.
11
* Frandsen et al., 2006

12. Power Generation Model Validation
The model is validated against data from a wind
tunnel experiment* on a scaled down wind farm.
12
For Turbine-8
Parameter Model Experiment
U 6.71 m/s 6.24 m/s
P 0.336 W 0.34 W
Cp 0.16 0.21
a 0.085 0.087
* Cal et al., 2010

13. Wind Farm Cost Model
• Quadratic response surface based cost models are developed to represent the
farm cost, as a function of the turbine rotor diameters.
• To this end we used data for wind farms in the state of New York*
For wind farm with non-identical turbines
13
* Wind and Hydropower Technologies program (US Department of Energy)

14. Particle Swarm Optimization (PSO)
Swarm Motion*
t  1 t t

1
i i i
t t t t
i i l i i g g i
x x v
v  v  r p x  r p x
   
1
1 2

 
    
Solution Comparison
The constraint dominance principle**
is used.
PSO can appropriately address the
non-linearity and the multi-modality of
the wind farm model.
14
* Kennedy and Eberhart, 1985
** Deb et al., 2002

15. UWFLO – Problem Definition
• An unidirectional uniform wind at 7.09 m/s and at 0o to X-axis is considered.
15

16. 16
UWFLO – Realistic Power Curve
Case 1 (Case 3 in the paper)
• Identical turbines, with rotor diameter = 0.12m, is considered here.
• Modified power curve: The power generated is assumed to remain constant
at the rated power (0.385W) for U > Rated speed (6.17m/s)

17. UWFLO Results – Non-Identical Turbines
17
Case 2
• Turbines with differing rotor diameters are considered: 0.08m – 0.16m.
• Additional inequality constraint g3 is applied to constraint the cost of the
wind farm.
• The same original power curve is used for each turbine.
Number of Function Evaluations
Objective Function, f
5000 10000 15000 20000 25000
1.05
1.00
0.95
0.90
0.85
0.80
0.75
1 2
3
4
5
6
7
8
9
X - coordinate
Y - coordinate
0.0 0.5 1.0 1.5
1.0
0.5
0.0
-0.5
Turbine Number
D (m)
0 1 2 3 4 5 6 7 8 9 10
0.16
0.14
0.12
0.1
0.08
Incoming
Wind Speed

18. Concluding Remarks
 The proposed UWFLO technique avoids limiting assumptions, regarding the
farm layout and choice of wind turbines.
 Reasonable agreement is obtained between the UWFLO model and the
corresponding experimental data.
 Layout optimization with identical turbines produced a 30% increase in farm
efficiency compared to the 3x3 array layout.
 The use of turbines with differing rotor diameters has the potential to increase
the farm efficiency significantly (43% compared to the array layout).
18

19. Future Work
 Current research is investigating the effects of other critical factors in
wind farm planning; namely the number of turbines and the farm size.
 A recently developed mixed-discrete optimization methodology is being
implemented to appropriately represent the use of non-identical turbines.
 Future research will also consider the variability of the speed and
direction of wind, in the case of commercial wind farms.
19

20. Selected References
1. World Wind Energy Report 2008. Bonn, Germany, February 2009.
2. Katic, I., Hojstrup, J., and Jensen, N. O. A Simple Model for Cluster Efficiency. In Proceedings of European
Wind Energy Conference and Exhibition (Rome, Italy 1986).
3. Frandsen, S., Barthelmie, R., Pryor, S, Rathmann, O, Larsen, S, Hojstrup, J, and Thogersen, M. Analytical
Modeling of Wind Speed Deficit in Large Offshore Wind Farms. Wind energy, 9, 1-2 (2006), 39-53.
4. Grady, S. A., Hussaini, M. Y., and Abdullah, M. M. Placement of Wind Turbines Using Genetic Algorithms.
Renewable Energy, 30, 2 (February 2005).
5. Sisbot, S., Turgut, O., Tunc, M., and Camdali, U. Optimal positioning of Wind Turbines on Gökçeada Using
Multi-objective Genetic Algorithm. Wind Energy (2009).
6. Mosetti, G., Poloni, C., and Diviacco, B. Optimization of Wind Turbine Positioning in Large Wind Farms by
Means of a Genetic Algorithm. Journal of Wind Engineering and Industrial Aerodynamics, 54, 1 (January
1994), 105-116.
7. Kennedy, J. and Eberhart, R. C. Particle Swarm Optimization. In Proceedings of the 1995 IEEE International
Conference on Neural Networks ( 1995), 1942-1948.
8. Cal, R. B., Lebron, J., Kang, H.S., Meneveau, C., and Castillo, L., “Experimental study of the horizontally
averaged flow structure in a model wind-turbine array boundary layer”, Journal of Renewable and
Sustainable Energy, 2, 1 (2010).
9. Lebron, J., Castillo, Cal, R. B., Kang, H. S., and Meneveau, C., 2010, “Interaction Between a Wind Turbine
Array and a Turbulent Boundary Layer,” Proceeding 49th AIAA Aerospace Sciences Meeting including the
New Horizons Forum and Aerospace Exposition, January 4-9.
20

21. Acknowledgement
21
Thank you

22. Questions
or
Comments
22