This document covers arithmetic sequences, including defining arithmetic sequences as sequences where each term is obtained by adding a constant to the previous term. It provides examples of determining whether a sequence is arithmetic and calculating the nth term and sum of terms using formulas. The document also discusses inserting arithmetic means between terms and solving problems involving arithmetic sequences.

1. Arithmetic
Sequence
Lesson 2

2. Objectives
Illustrates an arithmetic sequence
Determines nth term of an arithmetic
sequence

3. Trivia:
• The Egyptians were the first one to develop the arithmetic
sequence.
• Carl Gauss, in 1777 at 10 years old created a formula to
solve for the sum of arithmetic sequence.

4. Observe the given
pattern
5 terms
2 5 8 1
1
14
+
3
+
3
+
3
+
3
Rule – add
3
Common
difference
ARITHMETIC
SEQUENCE

5. ARITHMETIC
SEQUENCE
or “ARITHMETIC
PROGRESSION”
is a sequence where every term is added a constant number
to get the next term.
d = common
difference
Increasing arithmetic
Sequence
= common difference is
POSITIVE
Decreasing arithmetic
Sequence
= common difference is
NEGATIVE

6. ARITHMETIC
SEQUENCE
23, 30, 37, 44, 51
Common difference is obtained by
getting the difference of two consecutive
terms of arithmetic sequence.
30 - 27 = 7
7
37 - 30 = 7
44 - 37 = 7
51 - 44 = 7
7 7 7
Common difference = 7
INCREASING

7. Determine whether the given sequence is an
arithmetic sequence and if yes, identify the
common difference
2. 19, 13, 7, 1, -5
3. 8, 17, 26, 35, 44
4. 10, 7, 4, 1, 0
Arithmetic Sequence d = -6
Arithmetic Sequence d = 9
Not Arithmetic Sequence

8. The arithmetic sequence has 5 terms. The
first term is -3 and each term is added by
4. What is the arithmetic sequence?
a
1
a
2
a
3
a
4
a
5
-3 d = 4
+4
1
+4 +4 +4
5 9 1
3

9. 3, 7, 11, 15, 19, … d = 4
a
1 a
2
a
3
a
4
a
5
100th term
a100

10. Arithmetic formula
𝒂𝒏 = 𝒂𝟏 + 𝒏 − 𝟏 𝒅
an = nth term of the sequence
a1 = first term
n = number of term
d = common difference

11. What is the 100th term of the sequence
3, 7, 11, 15, 19, … ?
𝒂𝒏 = 𝒂𝟏 + 𝒏 − 𝟏 𝒅
𝒏 = 𝟏𝟎𝟎 𝒂𝟏 = 𝟑 𝒅 = 𝟒
𝒂𝟏𝟎𝟎 = 𝟑 + 𝟏𝟎𝟎 − 𝟏 𝟒
𝒂𝟏𝟎𝟎 = 𝟑 + (𝟗𝟗)𝟒
𝒂𝟏𝟎𝟎 = 𝟑 + 𝟑𝟗𝟔
𝒂𝟏𝟎𝟎 = 𝟑𝟗𝟗

12. What is the 27th term of the sequence
35, 29, 23, 17, 11,… ?
𝒂𝒏 = 𝒂𝟏 + 𝒏 − 𝟏 𝒅
𝒏 = 𝟐𝟕 𝒂𝟏 = 𝟑𝟓 𝒅 = −𝟔
𝒂𝟐𝟕 = 𝟑𝟓 + 𝟐𝟕 − 𝟏 − 𝟔
𝒂𝟐𝟕 = 𝟑𝟓 + 𝟐𝟔 (−𝟔)
𝒂𝟐𝟕 = 𝟑𝟓 + (−𝟏𝟓𝟔)
𝒂𝟐𝟕 = −𝟏𝟐𝟏

13. Solve for the following Arithmetic Sequence
1. Find the 46th term of the arithmetic sequence 3, 8, 13, 18,
23, 28.
2. Find the 25th term of the arithmetic sequence 16, 13, 10, 7,
4.
3. Find the 31st term of the arithmetic sequence 15, 23, 31,
39,…

14. Solve for a35
Solve for a53

15. Activity 1
Solve the indicate nth term of the problem
1. What is the 27th term of the arithmetic sequence
:
-21, -23, -25, -27
2. Find the a36 in the arithmetic sequence: -4, -1, 2,
5, …

16. ARITHMETIC SEQUENCE INVOLVING
ALGEBRAIC EXPRESSION
Example:
1. The 16th term of an arithmetic sequence is 48. if the common
difference is 3. find the first term.
2. The 4th term of an arithmetic sequence is 18 and the 6th term is
28. give the first 3 terms.
3. Find the 7th term of an arithmetic sequence if the third term is 5
and the 5th term is 11
4. If a1 = 5, an = 395, and d = 5, find the value of n

17. ARITHMETIC SEQUENCE INVOLVING
ALGEBRAIC EXPRESSION
Example:
5. If a1 = 2.5. d = 1.5 and an = 13, find the vale of n.
6. In arithmetic sequence 8, 5, 2, - 1, …, what term is -
25?
7. If a1 = 5 and a7 = 17, find the common difference.
8. If a1 = 4 and a5 = 28, find the common difference.

18. Arithmetic means
The terms of an arithmetic sequence that
are between two given terms are called
arithmetic means. In the arithmetic
sequence 5, 8, 11, 14, 17, there are three
arithmetic means between 5 and 17. These
are 8, 11, and 14.

19. Arithmetic means
Example 1: insert three arithmetic
means between 17 and 1
Example 2: insert 4 arithmetic means
between 5 and 25

20. Arithmetic means
Insert the indicated number of arithmetic
means between the given first and last
terms of an arithmetic sequence
1.2 and 32 insert 1 term
2.6 and 54 insert 3 terms
3.68 and 3 insert 4 terms
4.10 and 40 insert 5 terms
5.½ and 2 insert 2 terms

21. Arithmetic Series
The secret of Karl Gauss
What is
1+2+3+…..+50+51+……+98+99+100=
A famous story tells that this was the
problem given by an elementary school
teacher to a famous mathematician to keep
him busy. Do you know that he was able to
get the sum within seconds only? Can you
beat that? His name was Karl Friedrich
Gauss. Do you know how he did it?

22. Arithmetic Series
Sn =
𝑛
2
[2a1 + (n-1) d ]
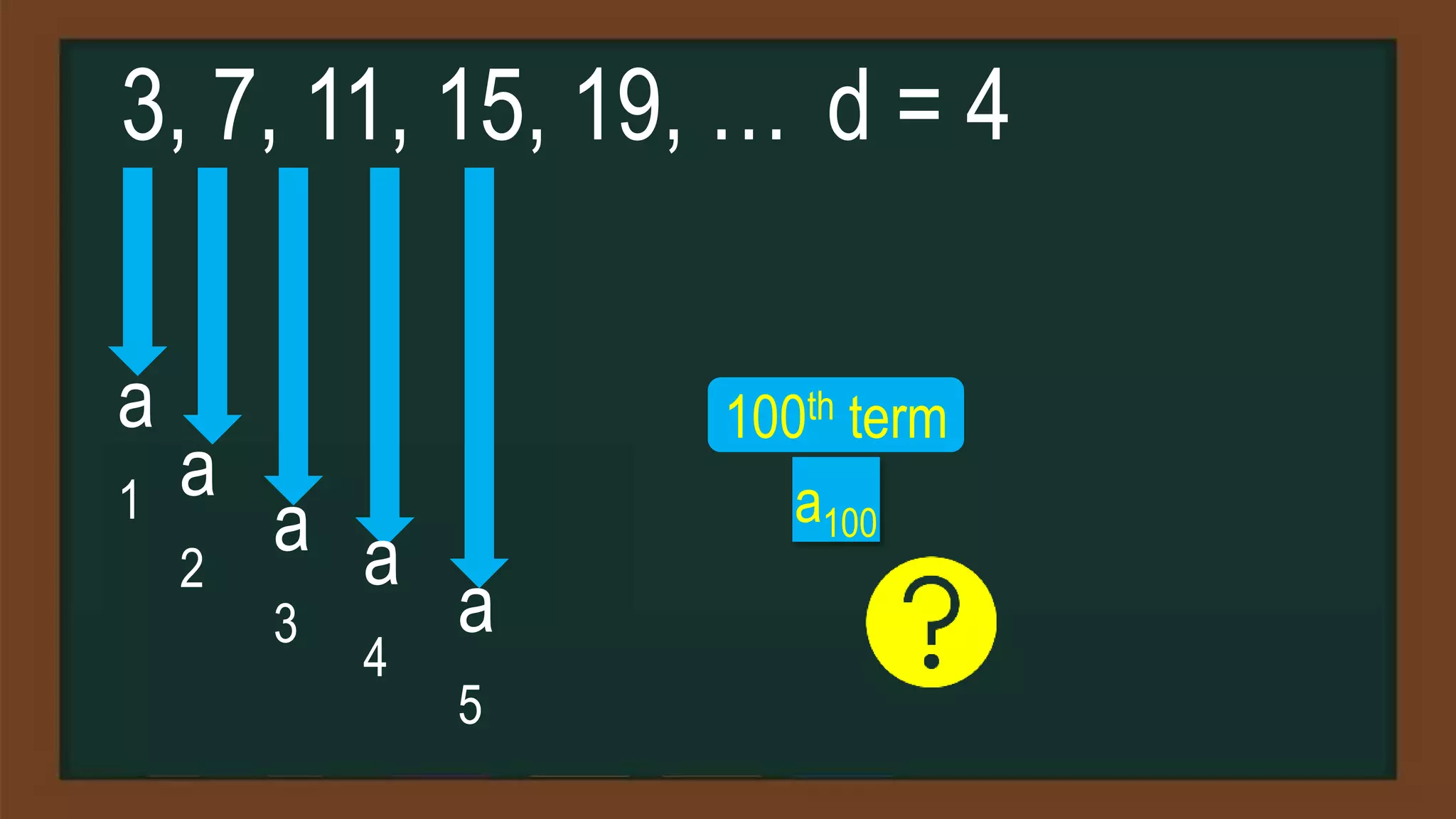
Example 1: find the sum of the first 10 terms
of the arithmetic sequence 5, 9, 13, 17, …
Example 2: find the sum of the first 20 terms
of the arithmetic sequence -2, -5, -8, -11, ….

23. Arithmetic Series
Sn =
𝑛
2
[2a1 + (n-1) d ]
•Integers from 1 to 50
•Odd integers from 1 to 100
•Even integers between 1 and 101
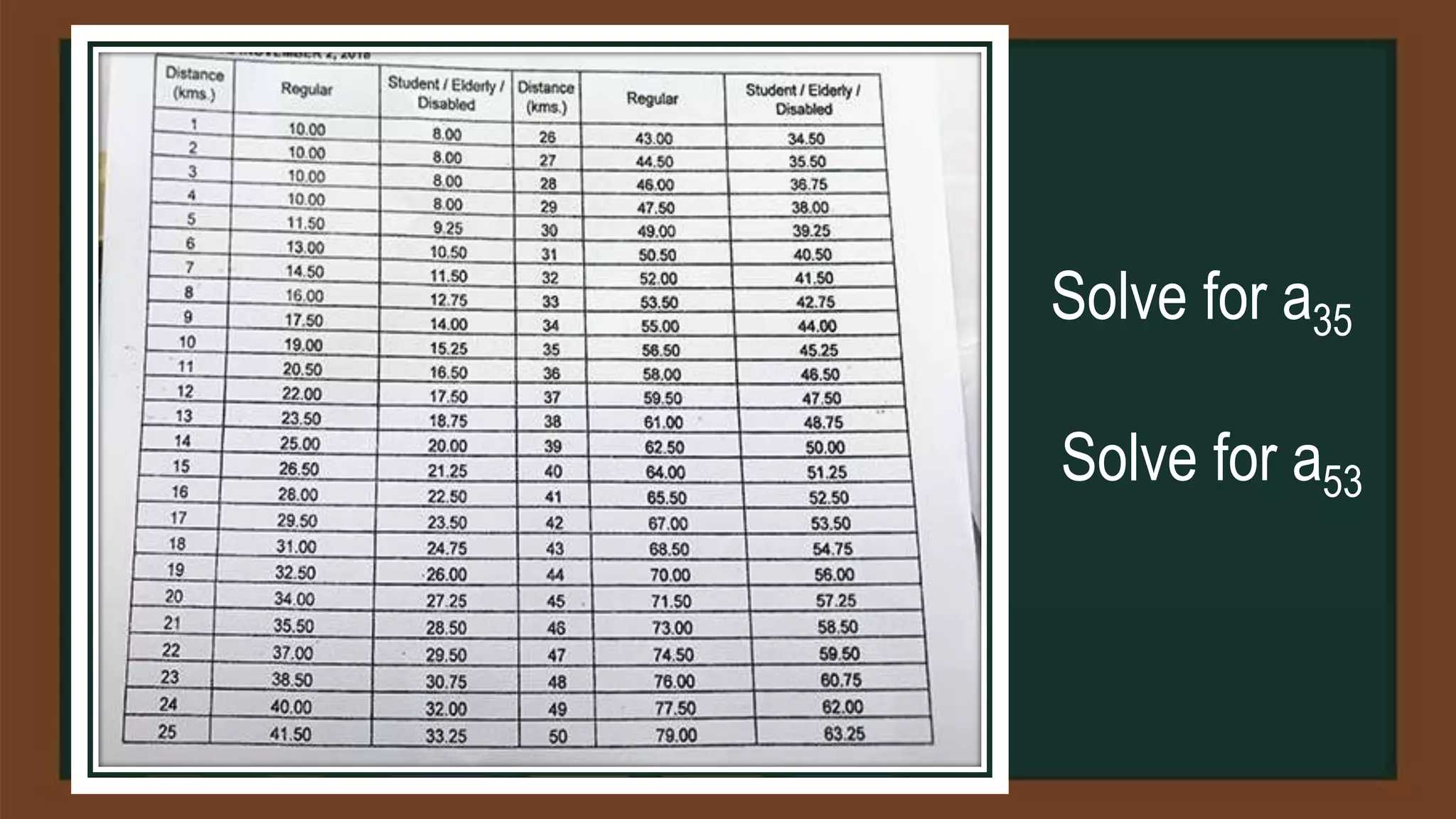
•First 25 terms of the arithmetic sequence
4, 9, 14, 19, 24
•Multiple of 3 from 15 to 45

24. Test I. Solve the following problems involving arithmetic sequence.
1. Find the 33rd term in the arithmetic sequence 8, 12, 16, 20, …
2. Find the 42nd term in the arithmetic sequence 5, 10, 15, …
3. The 1st term of an arithmetic sequence is 2 while the 18th term is 87. Find
the common difference of the sequence.
4. Insert 2 arithmetic means between 1 and 16.
5. Insert 4 arithmetic means between 8 and -7.
6. Insert 4 arithmetic means between 72 and 52.
7. Insert 6 arithmetic means between 16 and 2.
8. Find the sum of the first fifteen terms of the arithmetic sequence 3, 6, 9,…
9. Find the sum of the first 20 even integers….
10. Find the sum of the first 36 terms of the arithmetic sequence -20, -23, -26,
-29…..

25. 1. 136
2. 210
3. d = 5
4. d= 5 A.M. = 6 & 11
5. d= -3 A.M. = 5, 2, -1, -4
6. d= -4 A.M. = 68, 64, 60, 56
7. d= -2 A.M. = 14, 12, 10, 8, 6 , 4
8. 360
9. 420
10.-2610