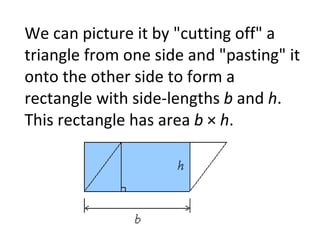
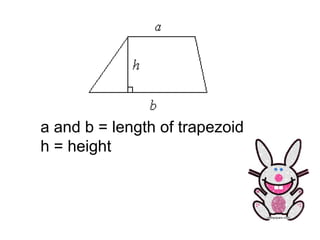
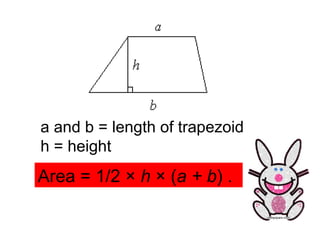
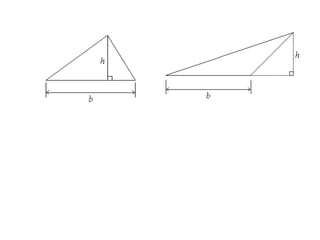
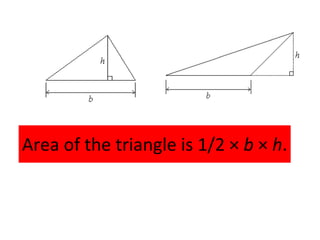
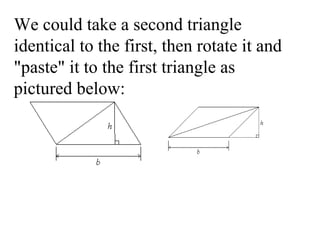
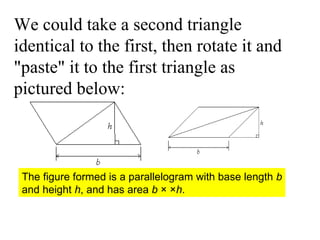
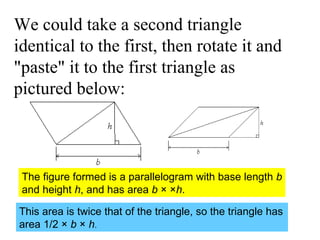
The document defines area and explains how to calculate the area of different shapes. It states that area measures the size of an enclosed region, usually in square units. To find the area of most shapes, you multiply the length by the width. It provides formulas for calculating the areas of rectangles, parallelograms, trapezoids, and triangles. For parallelograms and trapezoids, the base and height are used. For triangles, half the base times the height is used.

2. What is area???

3. The area of a figure measures the size of the region enclosed by the figure.

4. The area of a figure measures the size of the region enclosed by the figure. This is usually expressed in terms of some square unit.

5. Why we need to know the area???

6. In order to get the area, we need to now the:

7. In order to get the area, we need to now the: length (l) Width (d)

8. In order to get the area, we need to now the: length (l) Width (d) Then, we multiply length with width (l x d)

9. What size picture to fit the frame?

10. In order to know this, we must know the area of the frame and also the picture…

11. If the frame above has a length of 25cm and width 20 cm. then what is the area?

12. If the frame above has a length of 25cm and width 20 cm. then what is the area? A = 25cm x 20cm = 500

13. How about the area of Parallelogram???

14. The area of a parallelogram is b × h , where b is the length of the base of the parallelogram, and h is the corresponding height. To picture this, consider the parallelogram below: b = base h= height

15. We can picture it by "cutting off" a triangle from one side and "pasting" it onto the other side to form a rectangle with side-lengths b and h . This rectangle has area b × h .

16. Trapezoid

17. a and b = length of trapezoid h = height

18. a and b = length of trapezoid h = height Area = 1/2 × h × ( a + b ) .

19. In this, we consider two identical trapezoids, and "turn" one around and "paste" it to the other along one side as pictured below:

20. In this, we consider two identical trapezoids, and "turn" one around and "paste" it to the other along one side as pictured below: The figure formed is a parallelogram having an area of h × ( a + b ), which is twice the area of one of the trapezoids.

21. Triangle

23. Area of the triangle is 1/2 × b × h .

24. We could take a second triangle identical to the first, then rotate it and "paste" it to the first triangle as pictured below:

25. We could take a second triangle identical to the first, then rotate it and "paste" it to the first triangle as pictured below: The figure formed is a parallelogram with base length b and height h , and has area b × × h .

26. We could take a second triangle identical to the first, then rotate it and "paste" it to the first triangle as pictured below: The figure formed is a parallelogram with base length b and height h , and has area b × × h . This area is twice that of the triangle, so the triangle has area 1/2 × b × h .

27. So… clear with it???