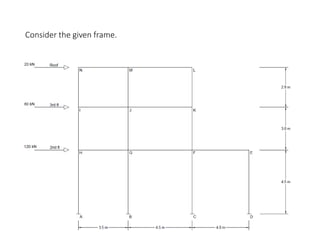
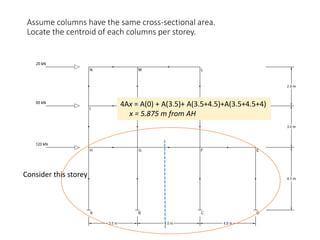
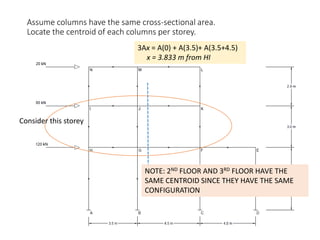
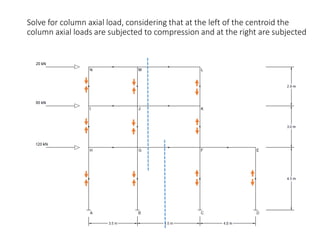
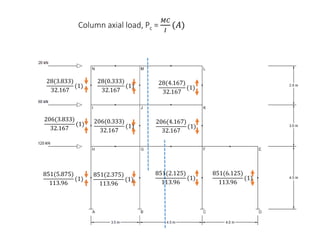
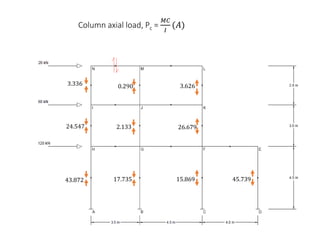
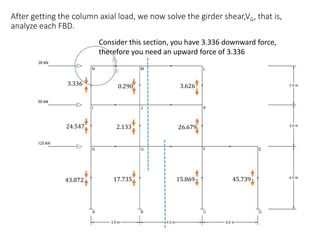
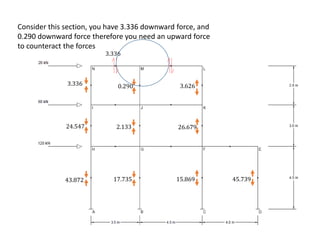
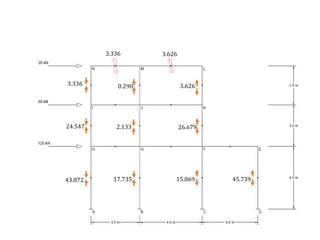
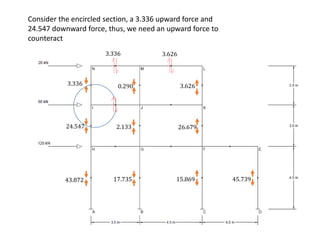
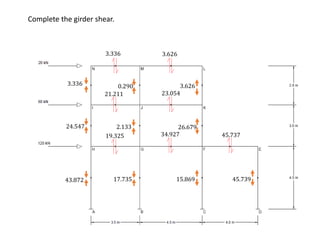
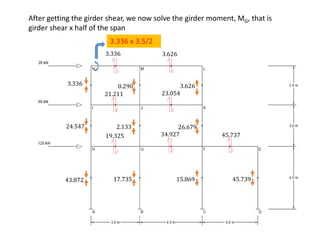
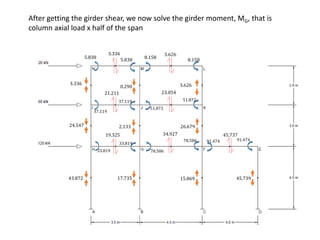
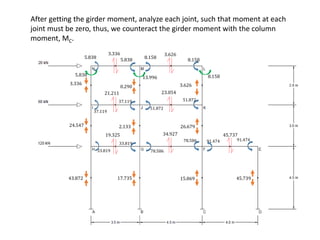
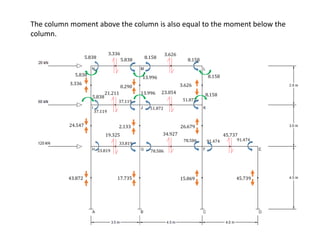
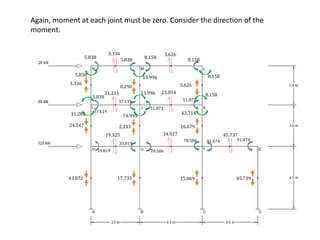
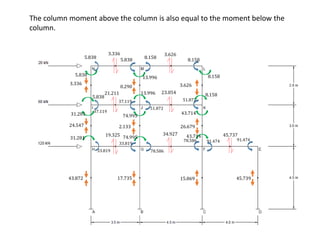
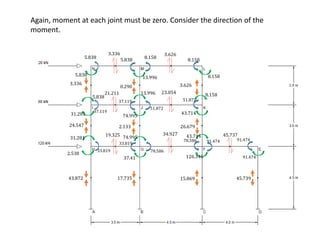
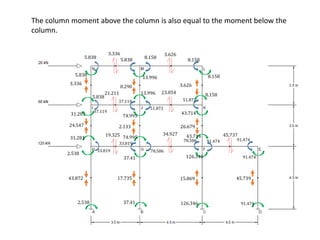
This document describes a cantilever method for calculating lateral loads on building frames. It involves the following steps: 1) Locating the centroid of each column to calculate column axial loads. 2) Analyzing each frame balance diagram (FBD) to determine girder shear and moment. 3) Ensuring moment at each joint is zero by equating girder and column moments. 4) Calculating column moments and shears from girder moments and column heights. The method systematically works through each floor of the sample frame to calculate key structural forces and moments.

1. LATERAL LOADS ON
BUILDING FRAMES
CANTILEVER METHOD

2. Assumptions:
1. A hinged is placed at the center of each girder
and each column since this is assumed to be
point of zero movement.
Note: this internal hinges are placed at
midspan of girders and midheight of columns.

3. Consider the given frame.

4. Assume columns have the same cross-sectional area.
Locate the centroid of each columns per storey.
Consider this storey
4Ax = A(0) + A(3.5)+ A(3.5+4.5)+A(3.5+4.5+4)
x = 5.875 m from AH

5. Assume columns have the same cross-sectional area.
Locate the centroid of each columns per storey.
Consider this storey
3Ax = A(0) + A(3.5)+ A(3.5+4.5)
x = 3.833 m from HI
NOTE: 2ND FLOOR AND 3RD FLOOR HAVE THE
SAME CENTROID SINCE THEY HAVE THE SAME
CONFIGURATION

6. Solve for column axial load, considering that at the left of the centroid the
column axial loads are subjected to compression and at the right are subjected
to tension.

7. Considering the hinged at the midheight of each column, moment at the
centroid, M = 20(1.4) = 28 kN-m at the 3rd floor.
Then solve the moment of inertia, I
for 2nd floor and 3rd floor
I = Ad2 = 1 3.833 − 0 2 + 1 3.833 − 3.5 2 + 1 8 − 3.833 2 = 32.167
For ground floor
I = Ad2 = 1 5.875 − 0 2 + 1 5.875 − 3.5 2 + 1 8 − 5.875 2 +1 12 − 5.875 2
= 113.916
Considering the hinged at the midheight of each column, moment at the
centroid, M = 20(1.5+3) + 80(1.5) = 206 kN-m at the 2nd floor.
Considering the hinged at the midheight of each column, moment at the centroid,
M = 20(2.25+3+2.8) + 80(2.25+3) + 120(2.25) = 851 kN-m at the ground floor.

8. Column axial load, Pc =
𝑀𝐶
𝐼
(𝐴)
28(3.833)
32.167
(1)
28(0.333)
32.167
(1) 28(4.167)
32.167
(1)
206(3.833)
32.167
(1) 206(0.333)
32.167
(1)
206(4.167)
32.167
(1)
851(5.875)
113.96
(1)
851(2.375)
113.96
(1)
851(2.125)
113.96
(1)
851(6.125)
113.96
(1)

9. Column axial load, Pc =
𝑀𝐶
𝐼
(𝐴)
3.336 0.290 3.626
24.547 2.133 26.679
43.872 17.735 15.869 45.739

10. After getting the column axial load, we now solve the girder shear,VG, that is,
analyze each FBD.
3.336 0.290 3.626
24.547 2.133 26.679
43.872 17.735 15.869 45.739
Consider this section, you have 3.336 downward force,
therefore you need an upward force of 3.336

11. 3.336 0.290 3.626
24.547 2.133 26.679
43.872 17.735 15.869 45.739
3.336
Consider this section, you have 3.336 downward force, and
0.290 downward force therefore you need an upward force
to counteract the forces

12. 3.336 0.290 3.626
24.547 2.133 26.679
43.872 17.735 15.869 45.739
3.336 3.626

13. 3.336 0.290 3.626
24.547 2.133 26.679
43.872 17.735 15.869 45.739
3.336 3.626
Consider the encircled section, a 3.336 upward force and
24.547 downward force, thus, we need an upward force to
counteract

14. 3.336 0.290 3.626
24.547 2.133 26.679
43.872 17.735 15.869 45.739
3.336 3.626
21.211 23.054
19.325 34.927 45.737
Complete the girder shear.

15. 3.336 0.290 3.626
24.547 2.133 26.679
43.872 17.735 15.869 45.739
3.336 3.626
21.211 23.054
19.325 34.927 45.737
After getting the girder shear, we now solve the girder moment, MG, that is
girder shear x half of the span
3.336 x 3.5/2

16. 3.336
0.290 3.626
24.547 2.133 26.679
43.872 17.735 15.869 45.739
3.336 3.626
21.211 23.054
19.325 34.927 45.737
After getting the girder shear, we now solve the girder moment, MG, that is
column axial load x half of the span
5.838 5.838 8.158
8.158
37.119
37.119
51.872
51.872
33.819
33.819
78.586
78.586 91.474 91.474

17. 3.336
0.290 3.626
24.547 2.133 26.679
43.872 17.735 15.869 45.739
3.336 3.626
21.211 23.054
19.325 34.927 45.737
5.838 5.838 8.158
8.158
37.119
37.119
51.872
51.872
33.819
33.819
78.586
78.586 91.474 91.474
5.838
13.996 8.158
After getting the girder moment, analyze each joint, such that moment at each
joint must be zero, thus, we counteract the girder moment with the column
moment, MC.

18. 3.336
0.290 3.626
24.547 2.133 26.679
43.872 17.735 15.869 45.739
3.336 3.626
21.211 23.054
19.325 34.927 45.737
5.838 5.838 8.158
8.158
37.119
37.119
51.872
51.872
33.819
33.819
78.586
78.586 91.474 91.474
5.838
13.996 8.158
5.838
13.996 8.158
The column moment above the column is also equal to the moment below the
column.

19. 3.336
0.290 3.626
24.547 2.133 26.679
43.872 17.735 15.869 45.739
3.336 3.626
21.211 23.054
19.325 34.927 45.737
5.838 5.838 8.158
8.158
37.119
37.119
51.872
51.872
33.819
33.819
78.586
78.586 91.474 91.474
5.838
13.996 8.158
5.838
13.996 8.158
Again, moment at each joint must be zero. Consider the direction of the
moment.
31.281 74.995
43.714

20. 3.336
0.290 3.626
24.547 2.133 26.679
43.872 17.735 15.869 45.739
3.336 3.626
21.211 23.054
19.325 34.927 45.737
5.838 5.838 8.158
8.158
37.119
37.119
51.872
51.872
33.819
33.819
78.586
78.586 91.474 91.474
5.838
13.996 8.158
5.838
13.996 8.158
31.281 74.995
43.714
The column moment above the column is also equal to the moment below the
column.
31.281 74.995 43.714

21. 3.336
0.290 3.626
24.547 2.133 26.679
43.872 17.735 15.869 45.739
3.336 3.626
21.211 23.054
19.325 34.927 45.737
5.838 5.838 8.158
8.158
37.119
37.119
51.872
51.872
33.819
33.819
78.586
78.586 91.474 91.474
5.838
13.996 8.158
5.838
13.996 8.158
31.281 74.995
43.714
31.281 74.995 43.714
Again, moment at each joint must be zero. Consider the direction of the
moment.
2.538
37.41 126.346 91.474

22. 3.336
0.290 3.626
24.547 2.133 26.679
43.872 17.735 15.869 45.739
3.336 3.626
21.211 23.054
19.325 34.927 45.737
5.838 5.838 8.158
8.158
37.119
37.119
51.872
51.872
33.819
33.819
78.586
78.586 91.474 91.474
5.838
13.996 8.158
5.838
13.996 8.158
31.281 74.995
43.714
31.281 74.995 43.714
2.538
37.41 126.346 91.474
The column moment above the column is also equal to the moment below the
column.
2.538 37.41 126.346 91.474

23. 3.336
0.290 3.626
24.547 2.133 26.679
43.872 17.735 15.869 45.739
3.336 3.626
21.211 23.054
19.325 34.927 45.737
5.838 5.838 8.158
8.158
37.119
37.119
51.872
51.872
33.819
33.819
78.586
78.586 91.474 91.474
5.838
13.996 8.158
5.838
13.996 8.158
31.281 74.995
43.714
31.281 74.995 43.714
2.538
37.41 126.346 91.474
Finally, we solve for the column shear, Vc = Column moment / half of column
height.
2.538 37.41 126.346 91.474
4.17 9.997 5.827
28.854 49.997 29.143
0.282 16.627 56.154 40.655

24. To recap, here are the step-by-
step forces/moments to obtain:
After getting the centroid:
1. Column axial load, Pc
2. Girder shear, VG
3. Girder moment, MG
4. Column axial, Pc
5. Column moment, Mc
6. Column shear, VC