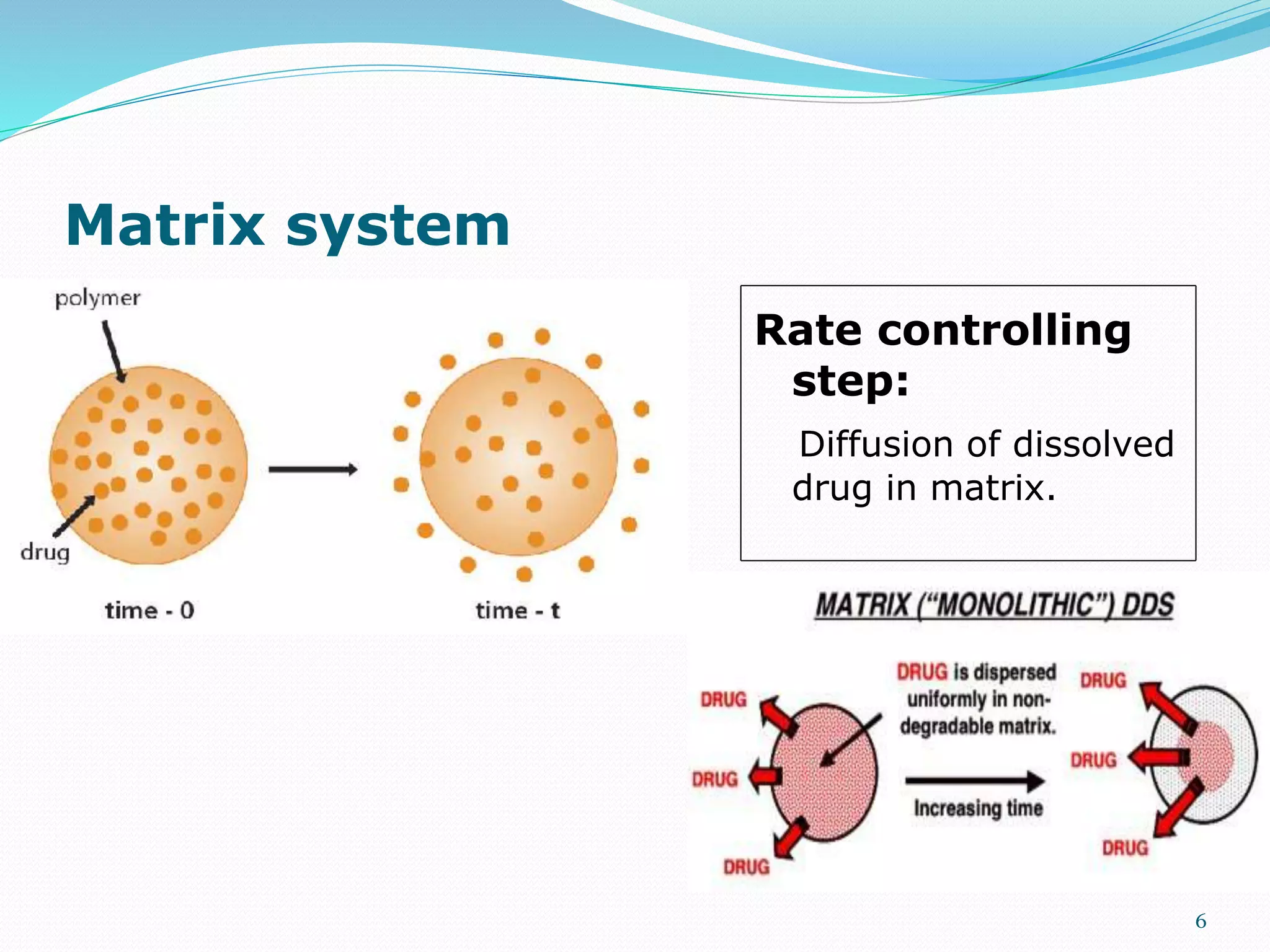
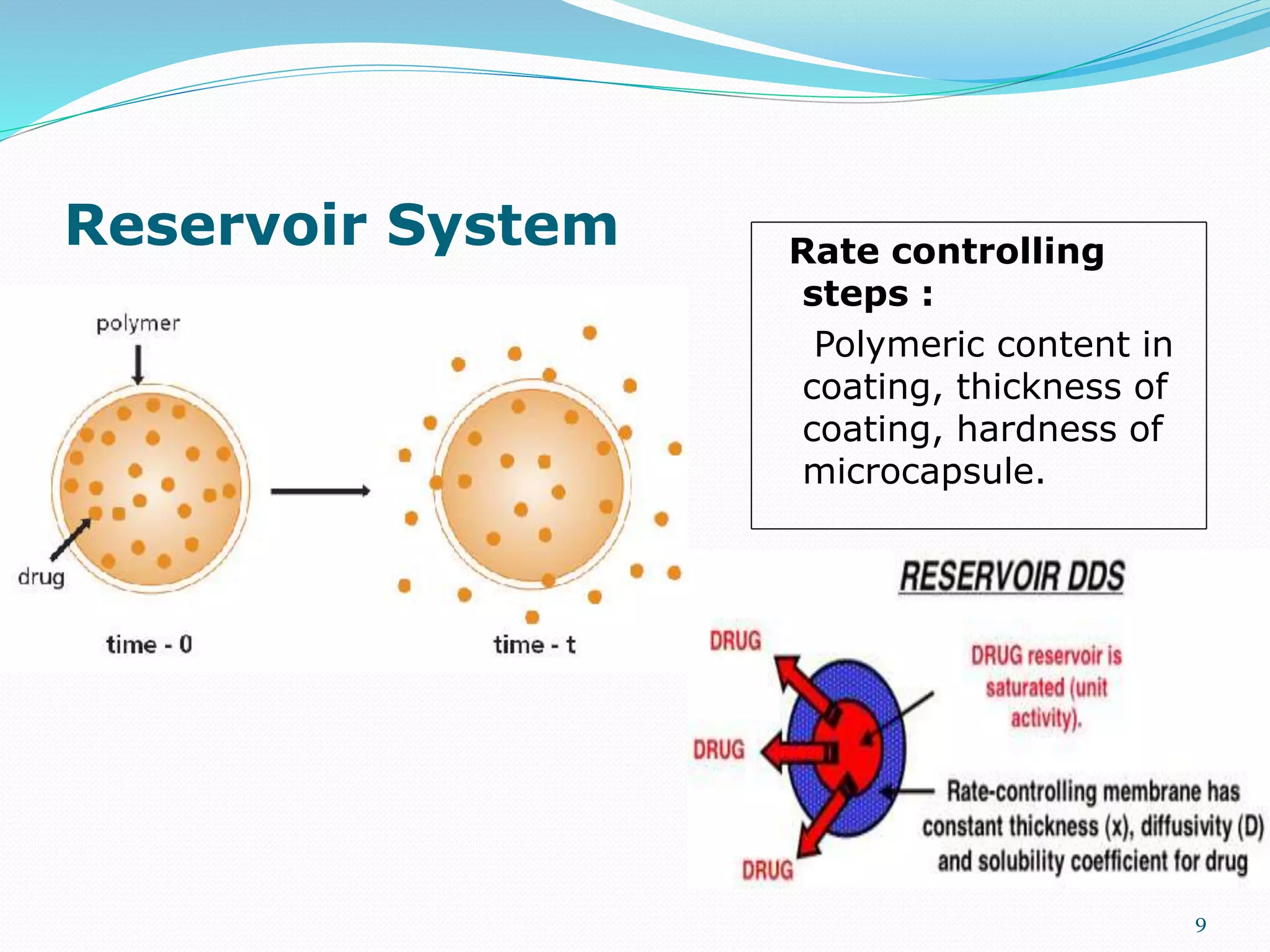
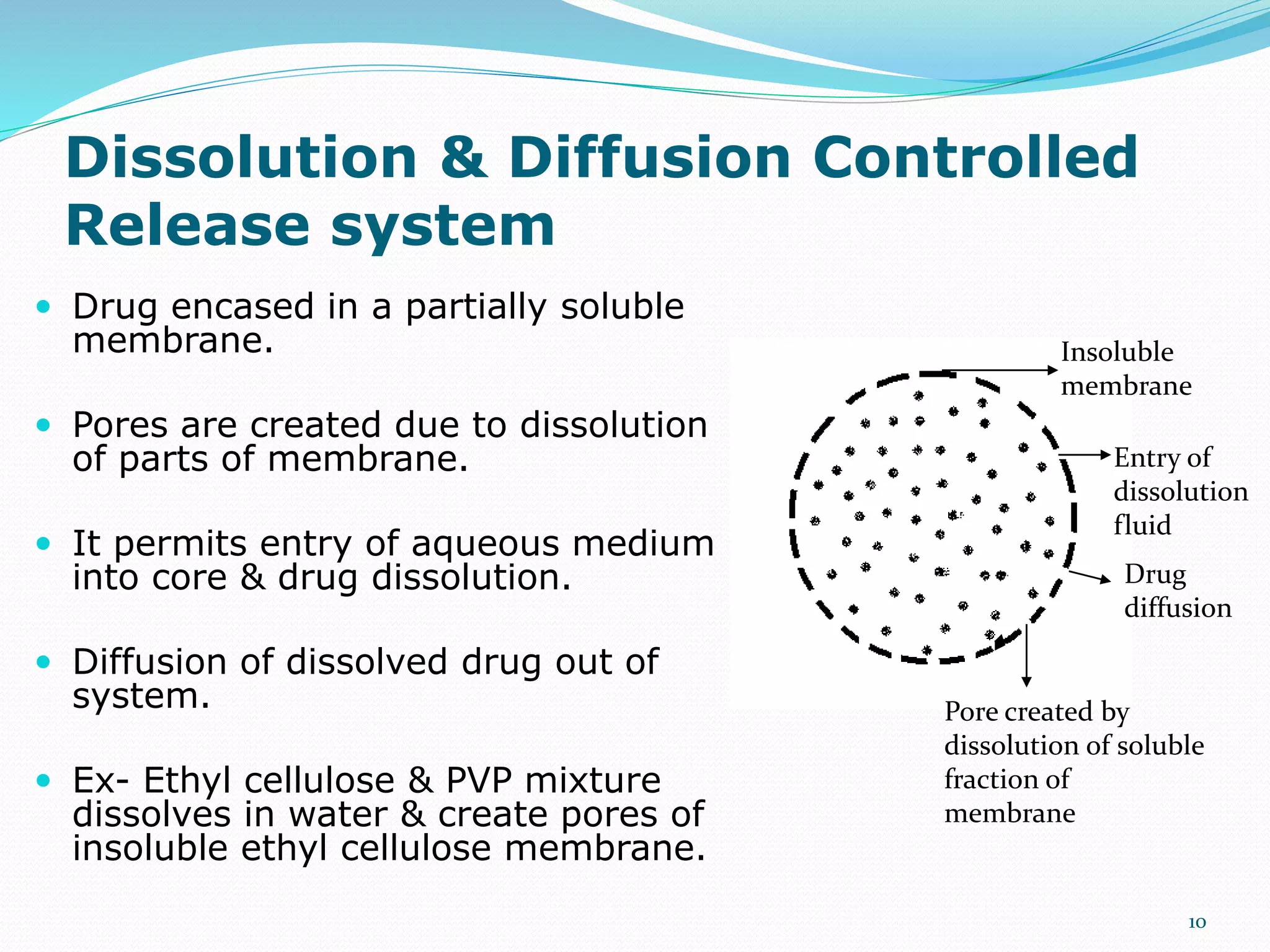
This presentation discusses kinetics of drug release from controlled release drug delivery systems. It describes different types of controlled release systems including matrix systems, reservoir systems, and dissolution-diffusion controlled systems. Rate controlling steps and drug release mechanisms such as diffusion, erosion, and dissolution are discussed. Factors influencing drug release and diffusion such as temperature, molecular weight, particle size, and viscosity are also summarized. Finally, mathematical models for drug release kinetics including zero-order, first-order, Higuchi, and Korsmeyer-Peppas models are presented.

1. PRESENTATION ON
KINETICS OF DRUG RELEASE
FROM THEORY OF MASS TRANSFER
1
Presented by
Vikas Aggarwal
M.Pharm (Ist sem)
Pharmaceutics

2. Matrix Type
 Also called as Monolith dissolution
controlled system.
 Controlled dissolution by:
1.Altering porosity of tablet.
2.Decreasing its wettebility.
3.Dissolving at slower rate.
 First order drug release.
 Drug release determined by
dissolution rate of polymer.
 Examples: Dimetane extencaps,
Dimetapp extentabs.
Soluble drug
Slowly dissolving matrix

3. Encapsulation
 Called as Coating dissolution
controlled system.
 Dissolution rate of coat depends
upon stability & thickness of coating.
 Masks colour,odour,taste,minimising
GI irritation.
 One of the microencapsulation
method is used.
 Examples: Ornade spansules,
Chlortrimeton Repetabs
3
Soluble drug
Slowly
dissolving or
erodible
coat

4. Diffusion
 Major process for absorption.
 No energy required.
 Drug molecules diffuse from a region of higher concentration to
lower concentration until equilibrium is attainded.
 Directly proportional to the concentration gradient across the
membrane.
4

5. Matrix Diffusion Types
 Rigid Matrix Diffusion
Materials used are insoluble plastics such as PVP & fatty
acids.
 Swellable Matrix Diffusion
1. Also called as Glassy hydrogels.Popular for sustaining
the release of highly water soluble drugs.
2. Materials used are hydrophilic gums.
Examples : Natural- Guar gum,Tragacanth.
Semisynthetic -HPMC,CMC,Xanthum gum.
Synthetic -Polyacrilamides.
Examples: Glucotrol XL, Procardia XL
5

6. Matrix system
Rate controlling
step:
Diffusion of dissolved
drug in matrix.
6

7. Higuchi Equation
Q = DE/T (2A.E Cs)Cs.t)1/2
Where ,
Q=amt of drug release per unit surface area at time t.
D=diffusion coefficient of drug in the release medium.
E=porosity of matrix.
Cs=solubility of drug in release medium.
T=tortuosity of matrix.
A=concentration of drug present in matrix per unit
volume.
7

8. Reservoir System
 Also called as Laminated matrix device.
 Hollow system containing an inner core surrounded in water
insoluble membrane.
 Polymer can be applied by coating or micro encapsulation.
 Rate controlling mechanism - partitioning into membrane with
subsequent release into surrounding fluid by diffusion.
 Commonly used polymers - HPC, ethyl cellulose & polyvinyl
acetate.
 Examples: Nico-400, Nitro-Bid
8

9. Reservoir System Rate controlling
steps :
Polymeric content in
coating, thickness of
coating, hardness of
microcapsule.
9

10. Dissolution & Diffusion Controlled
Release system
 Drug encased in a partially soluble
membrane.
 Pores are created due to dissolution
of parts of membrane.
 It permits entry of aqueous medium
into core & drug dissolution.
 Diffusion of dissolved drug out of
system.
 Ex- Ethyl cellulose & PVP mixture
dissolves in water & create pores of
insoluble ethyl cellulose membrane.
10
Insoluble
membrane
Pore created by
dissolution of soluble
fraction of
membrane
Entry of
dissolution
fluid
Drug
diffusion

11. FACTORS INFLUENCING DRUG RELEASE
1. Permeation-Depends on crystallinity,nature of polymer,its
degree of polymerization,presence of fillers and
plasticizers,matrix properties like
thickness,porosity,diffusion layer etc.
2. Diffusion-diffusion coefficient
3. Partition coeffficient-imp. when matrix contains drug
dissolved in polymer.
4. Solubility-imp when drug is not dissolved in polymer
matrix,rather dispersed.
5. Pharmaceutical manipulations-porosity,compression
pressure,coat thickness,plasticizer conc., polarity of coating
materials etc.

13. This is the one dimensional form of fick’s first law.
As long as we are at steady state,solutions to Fick’s first law
provides a completely adequate description of the diffusional
process.
When a drop of dye is placed in a beaker of water at constant
temp,the dye tends to diffuse throughout the water,eventually
giving the solution a uniform colour.Dye molecules can be
viewed as being in a state of continual random motion.As
such,each molecule can move in any direction with equal
probability.The reason that molecules diffuse away from their
source is that there are more dye molecules at the source than in
the bulk solution.Therefore more molecules can move away
from the source than towards the source.

14. In first case amt. in core changes but conc remains same inside
upto a particular time and undergoes dilution so that dC
becomes constt. So when concentrations are changing with
time,as in the case of above experiment,we may know dC/dX
at the beginning of experiment,but the mass flow will
continually be changing the conc. gradient.Therefore it is
necessary to introduce time as a variable.Eqn then becomes-
This equation is called Fick’s 2nd law of diffusion.
Interpretation from the equation-
Rate of change in conc. in volume element is proportional to
area of change of conc. gradient in that region of field.
Diffusion coefficient(D) is a measure of rate of drug movt.
J=[dC/dt]x=D[d²C/dX²]ᵼ

15. FACTORS INFLUENCING DIFFUSIVITY
 Temperature-Diffusion is a dynamic process.Movt of a molecule
in a particular build of matrix will take place based on enthalpy
of system.As the temp. is increased,D value increases.At higher
temp.,there will be a higher flux rate.
As per Arrhenius equation -
Or lnD=lnD₀‒Ed⁄RT
D₀=temp independent frequency factor i.e. all molecules are at rest
at 0⁰K
Ed=Energy of activation for polymer diffusion
 Molecular wt.-As molecular weight and mol. Volume related to
each other directly,because density is constt.As molecular wt
increases,there will be more amt of resistance to movt.
D=Dₒe¯ᴱᵈ/ᴿᵀ
D α (1/Mol. Wt)⅓

16. Factors continued……… Radius of particles .Particles are assumed to be
spherical,small and electrically neutral.We can find out the
diameter of particles and its diffusivity in any particular
media.
where Na=Avogadro’s no(no. of particles in any particular
system)
As radius increases ,diffusion decreases.
Ƞ=viscosity.As viscosity increases diffusion decreases
D=RT/Na(6πƞ)r

17. 4 Drug solubility As diffusion depends on conc gradient, drug solubility in
penetrant becomes important and then drug release becomes dissolution
dependent for sparingly soluble drugs . This can be expressed by Noyes –
Whitney eqn
Where dC/dt = Amt of drug release per unit time
K= dissolution rate constant
Cs= Saturation solubility in solvent
C = Conc in solvent at time t.
K= DsA/Vlb
Therefore Noyes- Whitney Eqn becomes
where Ds=diffusion coeff. in solvent
V=vol of soln.
dC/dt= DsA/Vlb (Cs-C)
dC/dt= K(Cs-C)
Time
Amt
releasing

18. DRUG DIFFUSION THROUGH MICROPARTICLES
When drug diffusion through microparticles/microcapsules is
concerned,drug transport involves dissolution of permeating
drug in polymer and diffusion across the membrane.
J=(DKA.ΔC/lm)
ΔC=conc difference on either side of membrane
lm=membrane thickness
K=partition coefficient of drug towards polymer
DK=permeability coefficient(imaginary)
DK/lm=permeability when lm is not known
D/lm=permeability constant(actual)
In case of nanoparticles of size 100 nm say and coat thickness
about 2nm or < 1nm,lm is insignificant,so DK/lm=DK only

19. Si-Nang and Carler eqn for drug release
from microcapsules
 dC/dt= [DsAK/Vlm]
 Where A= internal surface area of coating.
 K= Porosity and tortuosity.
Mechanisms/ Mathematical models of
drug release
1. First order
ln Xt = ln Xo+Kt (Release proportional to amount of
drug remaining )
Systems that follow the model – Water soluble drugs in
porus metrix

20. 2 Zero order
Ft= Kot (Release independent of drug conc)
Eg : Osmotic Systems, Transdermal systems
3 Higuchi eqn.
Ft= Kн t½
Eg :Diffusion matrix formulations
4 Khanna et al modified Noyes Whitney eqn. or
Hixson and Crowell’s cubic root low of dissolution
W0⅓-Wt⅓= Kaᵼ
Where Wo = Original mass of drug
Wt= mass of drug remaining to dissolve at time t.
aᵼ = surface wt fraction at time t

21. 5 Korsmeyer-Peppas eqn.
Mᵼ/Mₒ = Ktᵈ
Where Mᵼ/Mₒ fraction mass of drug released at time t.
Eg Hydrating sytems, Eroding systems where D is not
constant, thereby giving anomalous diffusion .
For Non-Fickian or anomalous diffusion m>0.5, which is
usually found in swellable systems

22. APPLICATIONS OF DRUG RELEASE DATA
1. Quality control
2. Understanding physiochemical aspects of drug delivery
system.
3. Understanding the release mechanisms.
4. Predict behaviour of system in vivo.
However there are difficulties in modelling drug release
data as there is great diversity in the physical form of
microcapsules/microparticles with respect to
size,shape,arrangement of core and coat,properties of
core like difffusivity,partition coeffficient,properties of
coat like porosity,thickness,crystallinity,inertness etc.

23. Brahmankar D.M., Jaiswal Sunil B.
“Biopharmaceutics and Pharmacokinetics A
Treatise Pg 408, 409,432.
Robinson Joseph R., Lee Vincent H.L.
“Controlled drug delivery Fundamentals and
Applications Pg 97, 101, 105.
Chien Yie W. “Novel Drug Delivery
systems” Pg 45,47,58,62,64,67.
REFERENCES