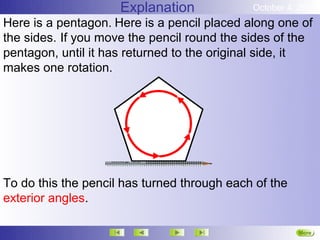
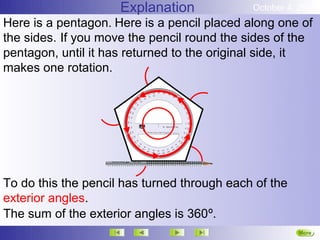
The document discusses angles in polygons. It states that the sum of the exterior angles of any convex polygon is 360 degrees. It also states that for any regular polygon, the sum of the interior and exterior angles at each vertex is 180 degrees. Finally, it provides a formula for calculating the sum of the interior angles of any n-sided convex polygon: the sum of the interior angles equals (180n - 360) degrees.

1. October 4, 2012
Angles
4. Angles in polygons
Next

2. Explanation October 4, 2012
Here is a pentagon. Here is a pencil placed along one of
the sides. If you move the pencil round the sides of the
pentagon, until it has returned to the original side, it
makes one rotation.
To do this the pencil has turned through each of the
exterior angles.
More
Next

3. Explanation October 4, 2012
Here is a pentagon. Here is a pencil placed along one of
the sides. If you move the pencil round the sides of the
pentagon, until it has returned to the original side, it
makes one rotation.
To do this the pencil has turned through each of the
exterior angles.
The sum of the exterior angles is 360º.
More

4. Explanation October 4, 2012
Heresamepentagon. Hereconvex polygon. along one of
The is a is true for any is a pencil placed
“The sum If the move in pencil round the sides of the
the sides. of you anglesthe any convex polygon is 360º”
pentagon, until it has returned to the original side, it
makes one rotation.
At any vertex, the interior and exterior angles form a
To do this the pencil has turned through each of the
straight line.
exterior angles. interior and exterior angles at the
“The sum of the
The sumof any regular polygon is 360º.
vertex of the exterior angles is 180º.”
More
Next

5. Example October 4, 2012
Here is an irregular pentagon, showing its exterior
angles.
a
60º
87º
67º
68º
78º
What is angle a?
Angle a = 360 – 87 += 60of the67
300 sum+ 78 + other angles
the 68
More
Next

6. Explanation October 4, 2012
This hexagon has six sides, and so six vertices.
The sum of the exterior plus interior angles is
180º × the number of sides = 180º × 6 = 1080º
As the sum of the exterior angles is 360º, you can
subtract this to find out the sum of the interior angles on
their own. 1080º – 360º = 720º so expressed in algebra
For any n-sided convex polygon:
the sum of the interior angles = (180n – 360)º
More
Next

7. Example October 4, 2012
Here is an irregular hexagon, showing its interior angles.
130º
120º
115º 120º
117º 118º
m
What is angle m?
m = (180n – 360)º – the sum of the other five angles
m = 720º – 603º
m = 117º
More
Next
End