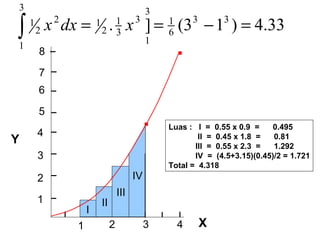
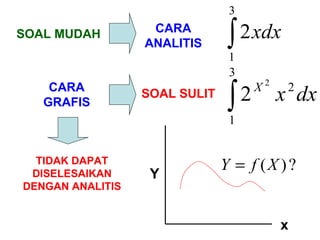
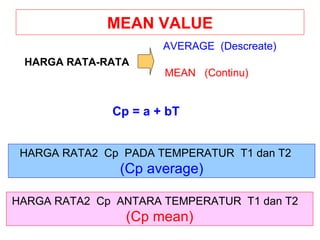
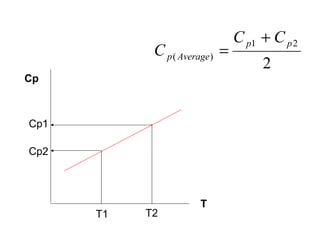
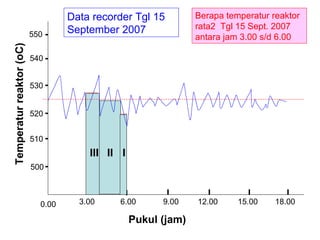
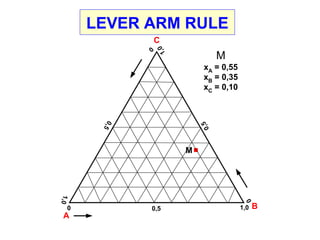
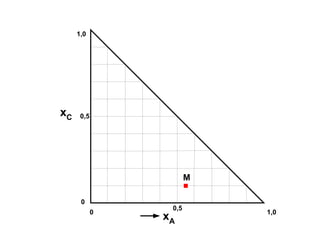
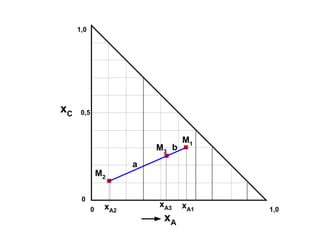
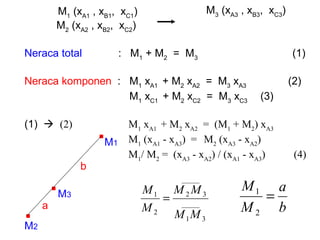
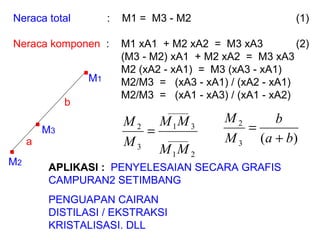
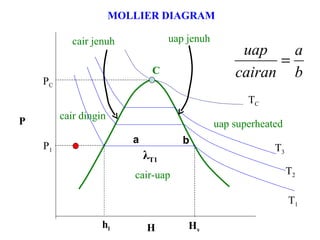
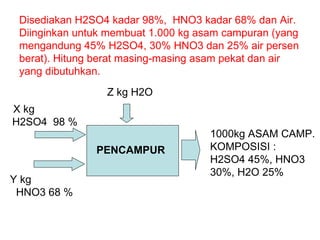
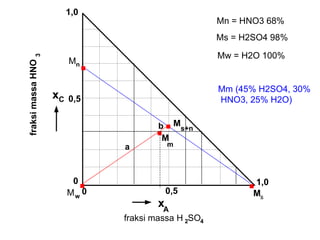
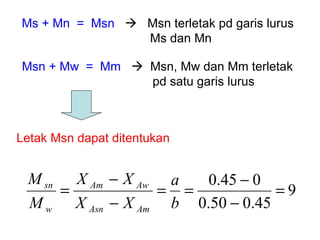
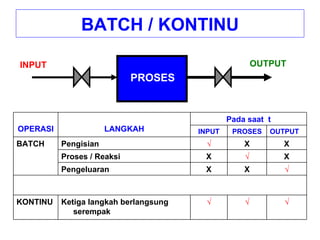
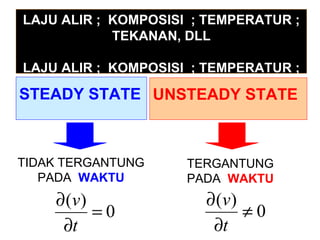
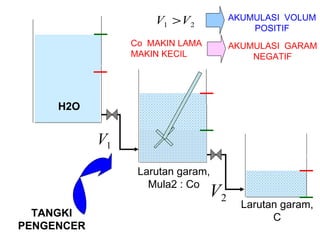
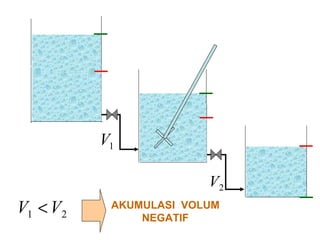
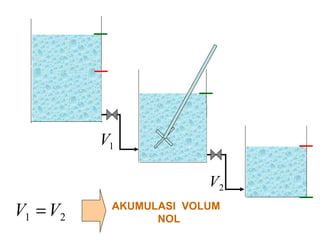
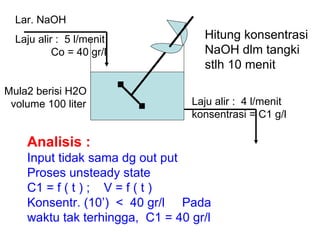
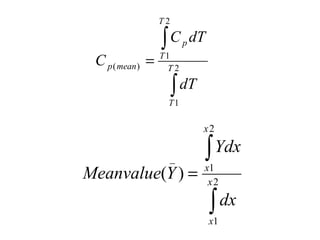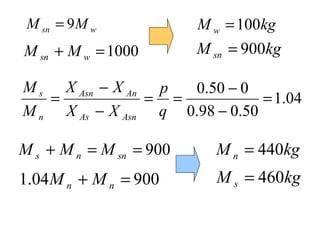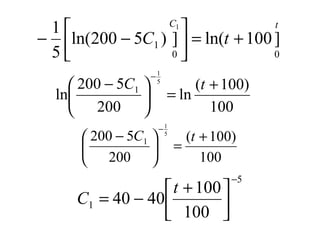Dokumen ini membahas metode integrasi grafis dan analitis dalam perhitungan integral untuk berbagai aplikasi dalam operasi unit, seperti menghitung suhu reaktor dan pengendalian proses. Pembahasan juga mencakup neraca massa, hukum kekekalan massa, dan pemodelan matematis untuk proses pencampuran serta distilasi. Contoh konkret dari perhitungan campuran asam dan konsentrasi larutan ditunjukkan untuk ilustrasi penerapan teori.

1. INTEGRASI SECARA GRAFIS . 1 2 3 4 5 6 X 1 2 3 4 5 6 Y

2. . . . . I II III IV Luas : I = 0.55 x 0.9 = 0.495 II = 0.45 x 1.8 = 0.81 III = 0.55 x 2.3 = 1.292 IV = (4.5+3.15)(0.45)/2 = 1.721 Total = 4.318 1 2 3 4 5 6 Y 7 8 1 2 3 4 X

3. SOAL MUDAH CARA ANALITIS CARA GRAFIS SOAL SULIT TIDAK DAPAT DISELESAIKAN DENGAN ANALITIS x Y

4. APLIKASI : PERHITUNGAN INTEGRAL PADA UNIT OPERATION : Menghitung tinggi cooling tower Menghitung waktu pengeringan, dll

5. MEAN VALUE HARGA RATA-RATA AVERAGE (Descreate) MEAN (Continu) Cp = a + bT HARGA RATA2 Cp PADA TEMPERATUR T1 dan T2 (Cp average) HARGA RATA2 Cp ANTARA TEMPERATUR T1 dan T2 (Cp mean)

6. Cp T Cp1 Cp2 T1 T2

8. 0.00 3.00 6.00 9.00 12.00 15.00 18.00 Pukul (jam) Temperatur reaktor (oC) 500 550 I II III Data recorder Tgl 15 September 2007 Berapa temperatur reaktor rata2 Tgl 15 Sept. 2007 antara jam 3.00 s/d 6.00 510 520 530 540

9. Luas I = 518 x 0.5 = 259 II = 524.5 x 1.4 = 734.3 III = 535 x 1.1 = 588.5 Luas total = 1581 (oC).jam

10. LEVER ARM RULE

13. M 1 (x A1 , x B1 , x C1 ) M 3 (x A3 , x B3 , x C3 ) M 2 (x A2 , x B2 , x C2 ) Neraca total : M 1 + M 2 = M 3 (1) Neraca komponen : M 1 x A1 + M 2 x A2 = M 3 x A3 (2) M 1 x C1 + M 2 x C2 = M 3 x C3 (3) (1)  (2) M 1 x A1 + M 2 x A2 = (M 1 + M 2 ) x A3 M 1 (x A1 - x A3 ) = M 2 (x A3 - x A2 ) M 1 / M 2 = (x A3 - x A2 ) / (x A1 - x A3 ) (4) . . . M 1 M 2 M 3 a b

14. Neraca total : M1 = M3 - M2 (1) Neraca komponen : M1 xA1 + M2 xA2 = M3 xA3 (2) (M3 - M2) xA1 + M2 xA2 = M3 xA3 M2 (xA2 - xA1) = M3 (xA3 - xA1) M2/M3 = (xA3 - xA1) / (xA2 - xA1) M2/M3 = (xA1 - xA3) / (xA1 - xA2) . APLIKASI : PENYELESAIAN SECARA GRAFIS CAMPURAN2 SETIMBANG PENGUAPAN CAIRAN DISTILASI / EKSTRAKSI KRISTALISASI. DLL . . M 1 M 2 M 3 a b

15. P H P C T C T 2 T 1 T 3 P 1 C H v h l λ T1 cair dingin cair jenuh uap jenuh uap superheated cair-uap MOLLIER DIAGRAM a b

16. Disediakan H2SO4 kadar 98%, HNO3 kadar 68% dan Air. Diinginkan untuk membuat 1.000 kg asam campuran (yang mengandung 45% H2SO4, 30% HNO3 dan 25% air persen berat). Hitung berat masing-masing asam pekat dan air yang dibutuhkan. X kg H2SO4 98 % Y kg HNO3 68 % Z kg H2O 1000kg ASAM CAMP. KOMPOSISI : H2SO4 45%, HNO3 30%, H2O 25% PENCAMPUR

17. x C 0 0 1,0 1,0 0,5 . . 0,5 a fraksi massa H 2 SO 4 fraksi massa HNO 3 b . . . Mm (45% H2SO4, 30% HNO3, 25% H2O) M s+n M w M m Mn = HNO3 68% Ms = H2SO4 98% Mw = H2O 100% M n M s x A

18. Ms + Mn = Msn  Msn terletak pd garis lurus Ms dan Mn Msn + Mw = Mm  Msn, Mw dan Mm terletak pd satu garis lurus Letak Msn dapat ditentukan

20. Cara Analitis : Neraca total : X + Y + Z = 1000 Neraca H2SO4 : 0.98X = 0.45(1000) Neraca HNO3 : 0.68Y = 0.30(1000) X = 459.2 kg Y = 441.2 kg Z = 99.6 kg

21. PEMODELAN MATEMATIS MASALAH FISIK Hukum Kekekalan Massa Pemodelan matematis pada proses : - Pencampuran, Pengenceran. - Distilasi batch

22. HUKUM KEKEKALAN MASSA / ENERGI JUMLAH / LAJU MASSA (ENERGI) MASUK SISTEM – JUMLAH / LAJU MASSA (ENERGI) KELUAR SISTEM = JUMLAH / LAJU AKUMULASI MASSA (ENERGI) DI DLM SISTEM INPUT – OUTPUT = AKUMULASI SISTEM Massa / Energi Massa / Energi Akumulasi Massa / Energi

23. BATCH / KONTINU √ √ √ Ketiga langkah berlangsung serempak KONTINU √ X X Pengeluaran X √ X Proses / Reaksi X X √ Pengisian BATCH OUTPUT PROSES INPUT Pada saat t LANGKAH OPERASI INPUT PROSES OUTPUT

24. VARIABEL PROSES LAJU ALIR ; KOMPOSISI ; TEMPERATUR ; TEKANAN, DLL LAJU ALIR ; KOMPOSISI ; TEMPERATUR ; TEKANAN, DLL STEADY STATE TIDAK TERGANTUNG PADA WAKTU UNSTEADY STATE TERGANTUNG PADA WAKTU

25. TANGKI PENGENCER H2O Larutan garam, Mula2 : Co Larutan garam, C AKUMULASI VOLUM POSITIF Co MAKIN LAMA MAKIN KECIL AKUMULASI GARAM NEGATIF

26. AKUMULASI VOLUM NEGATIF

27. AKUMULASI VOLUM NOL

28. Lar. NaOH Laju alir : 5 l/menit Co = 40 gr/l Laju alir : 4 l/menit konsentrasi = C1 g/l Mula2 berisi H2O volume 100 liter Hitung konsentrasi NaOH dlm tangki stlh 10 menit Analisis : Input tidak sama dg out put Proses unsteady state C1 = f ( t ) ; V = f ( t ) Konsentr. (10’) < 40 gr/l Pada waktu tak terhingga, C1 = 40 gr/l

29. Asumsi : Pada setiap titik dan setiap saat konsentrasi larutan dalam tangki homogen. Konsentrasi larutan keluar = konsentrasi dlm tangki Neraca total (laju alir volum) Dimana : V = volume larutan dalam tangki setiap saat (liter) t = waktu (menit) (1)

30. (2) Neraca komponen NaOH Laju NaOH (masuk tangki) – laju NaOH (keluar tangki) = laju NaOH (yang akumulasi dalam tangki) (3)

31. Substitusi pers(1) & (2) ke dalam pers (3) Pd t = 0 (mula2), konsentr. C dlm tangki = 0 (hanya berisi H2O)

32. Konsentrasi NaOH dalam tangki setelah 10 menit = 15.163 gr/l