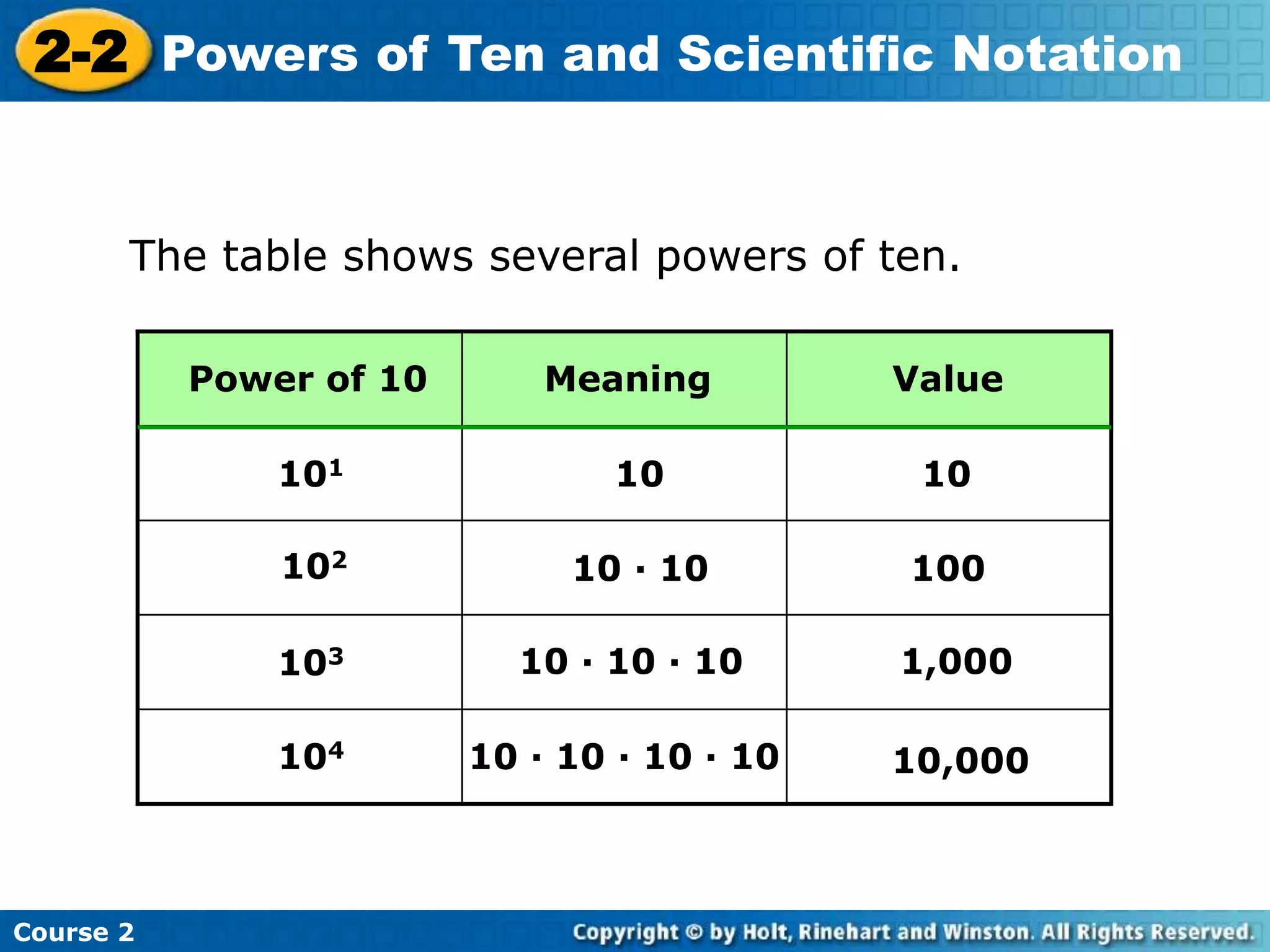
This document is a lesson on powers of ten and scientific notation. It begins with examples of multiplying numbers by powers of ten by moving the decimal point. It then explains how to write numbers in scientific notation as a number between 1 and 10 multiplied by a power of 10. Examples are provided of writing numbers in scientific notation and standard form. The document concludes with a quiz reviewing the concepts taught.

1. 2-2 Powers of Ten and Scientific Notation
Course 2
Warm Up
Problem of the Day
Lesson Presentation

2. 2-2 Powers of Ten and Scientific Notation
Warm Up
Find each value.
1. 92
3. 152
5. 103
81 144
225
Course 2
2. 122
4. 102 100
1,000 6. 104 10,000

3. 2-2 Powers of Ten and Scientific Notation
Problem of the Day
Each day, Lowell runs one more lap than
he did the day before. After seven days
he has run 77 laps. How many laps did
he run on the first day?
8
Course 2

4. 2-2 Powers of Ten and Scientific Notation
Learn to express large numbers in
scientific notation.
Course 2

5. 2-2 Powers of Ten and Scientific Notation
Insert Lesson Title Here
Vocabulary
standard form
scientific notation
Course 2

6. 2-2 Powers of Ten and Scientific Notation
Course 2
The distance from Venus to the Sun is over
100,000,000 kilometers. You can write this
number as a power of ten by using a base of
ten and an exponent.
10 · 10 · 10 · 10 · 10 · 10 · 10 · 10 = 108
Power of ten

7. 2-2 Powers of Ten and Scientific Notation
The table shows several powers of ten.
Course 2
Power of 10 Meaning Value
101
10 10
10 · 10
10 · 10 · 10
10 · 10 · 10 · 10
100
1,000
10,000
102
103
104

8. 2-2 Powers of Ten and Scientific Notation
Additional Example 1: Multiplying by Powers of Ten
Multiply 14 · 103.
Course 2
14 · 103 = 14 · (10 · 10 · 10)
= 14 · 1,000
= 14,000
Use 10 as a factor
3 times.
Multiply.

9. 2-2 Powers of Ten and Scientific Notation
Insert Lesson Title Here
Try This: Example 1
Multiply 12 · 102.
Course 2
12 · 102 = 12 · (10 · 10)
= 12 · 100
= 1,200
Use 10 as a factor
2 times.
Multiply.

10. 2-2 Powers of Ten and Scientific Notation
Course 2
You can also find the product of a number
and a power of ten simply by moving the
decimal point of the number. For powers of
ten with positive exponents, move the
decimal point to the right.

11. 2-2 Powers of Ten and Scientific Notation
Additional Example 2: Multiplying by Powers of Ten
Find each product.
Mentally
A. 212 · 104
Course 2
212 · 104 = 212.0000
= 2,120,000
4 places
Move the decimal point
4 places.
(You will need to add
4 zeros.)
B. 31.6 · 103
31.6 · 103 = 31.600
3 places
Move the decimal point
3 places.
= 31,600 (You will need to add
2 zeros.)

12. 2-2 Powers of Ten and Scientific Notation
Insert Lesson Title Here
Try This: Example 2
Find each product.
A. 22.5 · 102
Course 2
22.5 · 102 = 22.50
= 2,250
2 places
Move the decimal point
2 places.
(You will need to add
1 zero.)
B. 39.5 · 103
39.5 · 103 = 39.500
3 places
Move the decimal point
3 places.
= 39,500 (You will need to add
2 zeros.)

13. 2-2 Powers of Ten and Scientific Notation
Numbers are usually written in standard form.
For example, 17,900,000 is in standard form.
Scientific notation is a kind of shorthand that
can be used to write large numbers. Numbers
expressed in scientific notation are written as the
product of two factors. In scientific notation,
17,900,000 is written as
A number greater
than or equal to 1 but
less than 10
Course 2
A power of 10

14. 2-2 Powers of Ten and Scientific Notation
Writing Math
In scientific notation, it is customary to use
a multiplication cross () instead of a dot.
Course 2

15. 2-2 Powers of Ten and Scientific Notation
Additional Example 3A: Writing Numbers in Scientific
Notation
Write the number in scientific notation.
A. 4,340,000
4,340,000 = 4,340,000
Course 2
6 places
Move the decimal point to
get a number that is greater
than or equal to 1 and less
than 10.
= 4.34  106 The exponent is equal to
the number of places the
decimal point is moved.

16. 2-2 Powers of Ten and Scientific Notation
Additional Example 3B: Writing Numbers in Scientific
Notation
Write the number in scientific notation.
B. 327,000,000
327,000,000 = 327,000,000
Course 2
8 places
Move the decimal point to
get a number that is greater
than or equal to 1 and less
than 10.
= 3.27  108
The exponent is equal to
the number of places the
decimal point is moved.

17. 2-2 Powers of Ten and Scientific Notation
Insert Lesson Title Here
Try This: Example 3A
Write the number in scientific notation.
A. 8,421,000
8,421,000 = 8,421,000
Course 2
6 places
Move the decimal point to
get a number that is greater
than or equal to 1 and less
than 10.
= 8.421  106 The exponent is equal to
the number of places the
decimal point is moved.

18. 2-2 Powers of Ten and Scientific Notation
Insert Lesson Title Here
Try This: Example 3B
Write the number in scientific notation.
B. 327,000
327,000 = 327,000
Course 2
5 places
Move the decimal point to
get a number that is greater
than or equal to 1 and less
than 10.
= 3.27  105
The exponent is equal to
the number of places the
decimal point is moved.

19. 2-2 Powers of Ten and Scientific Notation
Additional Example 4: Writing Numbers in Standard
Form
The population of China in the year 2000 was
estimated to be about 1.262  109. Write this
number in standard form.
1.262  109 = 1.262000000
Course 2
Since the
exponent is 9,
move the decimal
point 9 places to
the right.
= 1,262,000,000
The population of China was about 1,262,000,000
people.

20. 2-2 Powers of Ten and Scientific Notation
Insert Lesson Title Here
Try This: Example 4
The distance from the Earth to the Sun is
calculated to be 1.5  108 kilometers. Write
this distance in standard form.
1.5  108 = 1.50000000 Since the exponent is
Course 2
8, move the decimal
point 8 places to the
right.
= 150,000,000
The distance from the Earth to the Sun is about
150,000,000 kilometers.

21. 2-2 Powers of Ten and Scientific Notation
Insert Lesson Title Here
Lesson Quiz: Part 1
Multiply.
2,500
180,000
Find each product.
11,000
3,742
1. 25  102
2. 18  104
3. 110  102
4. 3.742  103
Course 2

22. 2-2 Powers of Ten and Scientific Notation
Insert Lesson Title Here
Lesson Quiz: Part 2
Write each number in scientific notation..
5. 7,400,000
6. 45,000
7.4  106
4.5 104
7. Earth is about 9.292  107 miles from the Sun.
Write this number in standard form.
92,920,000
Course 2