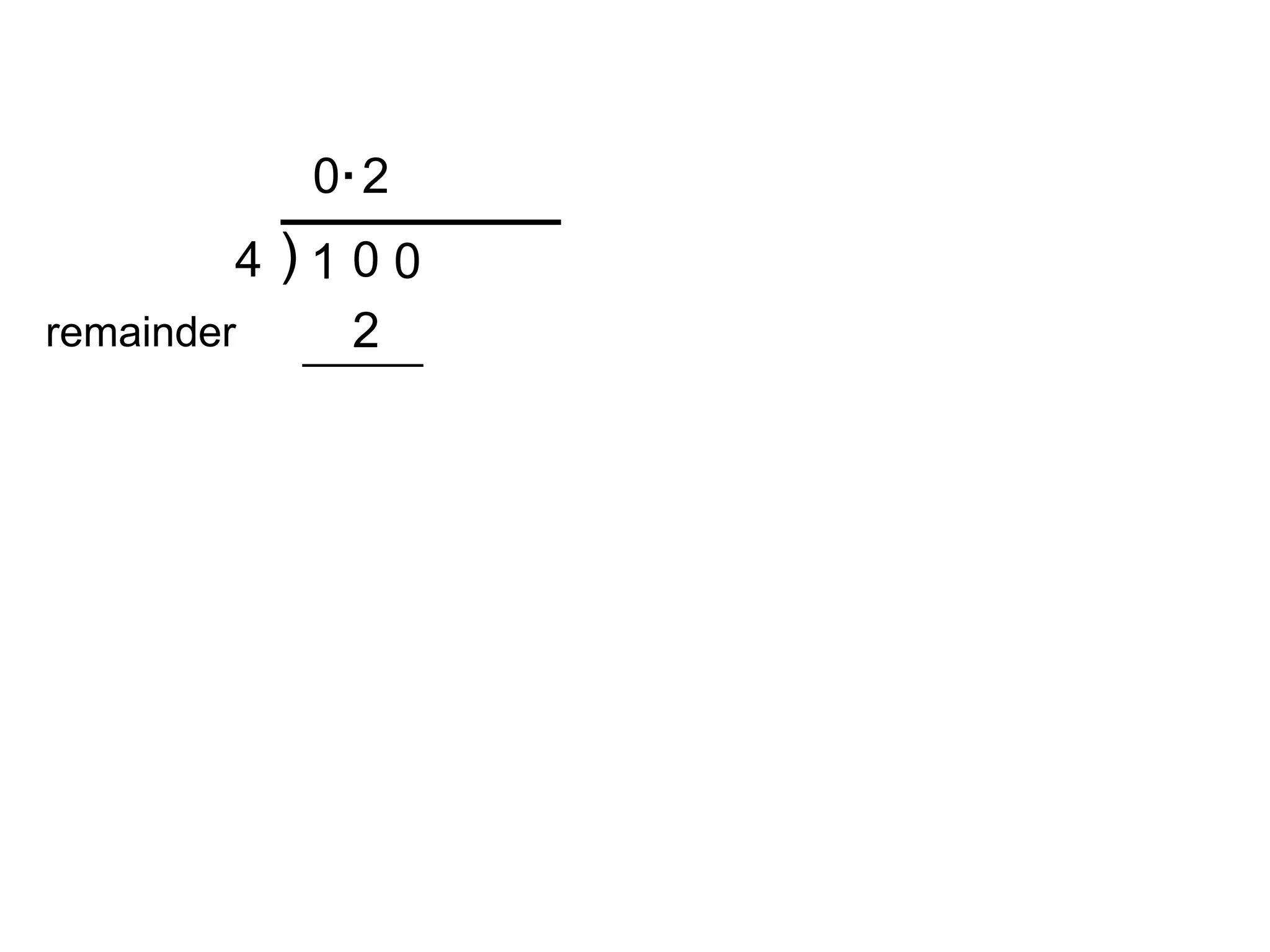
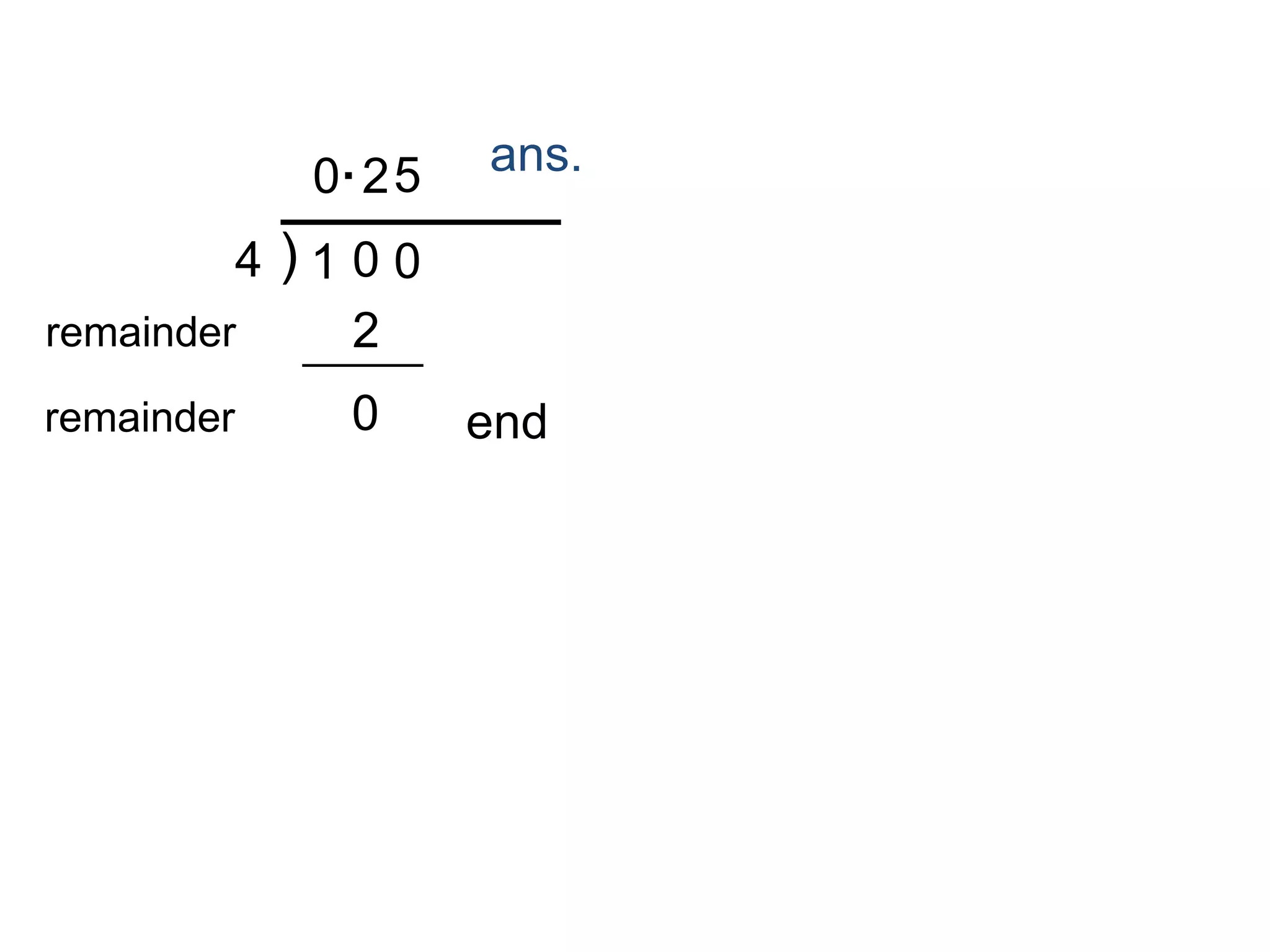
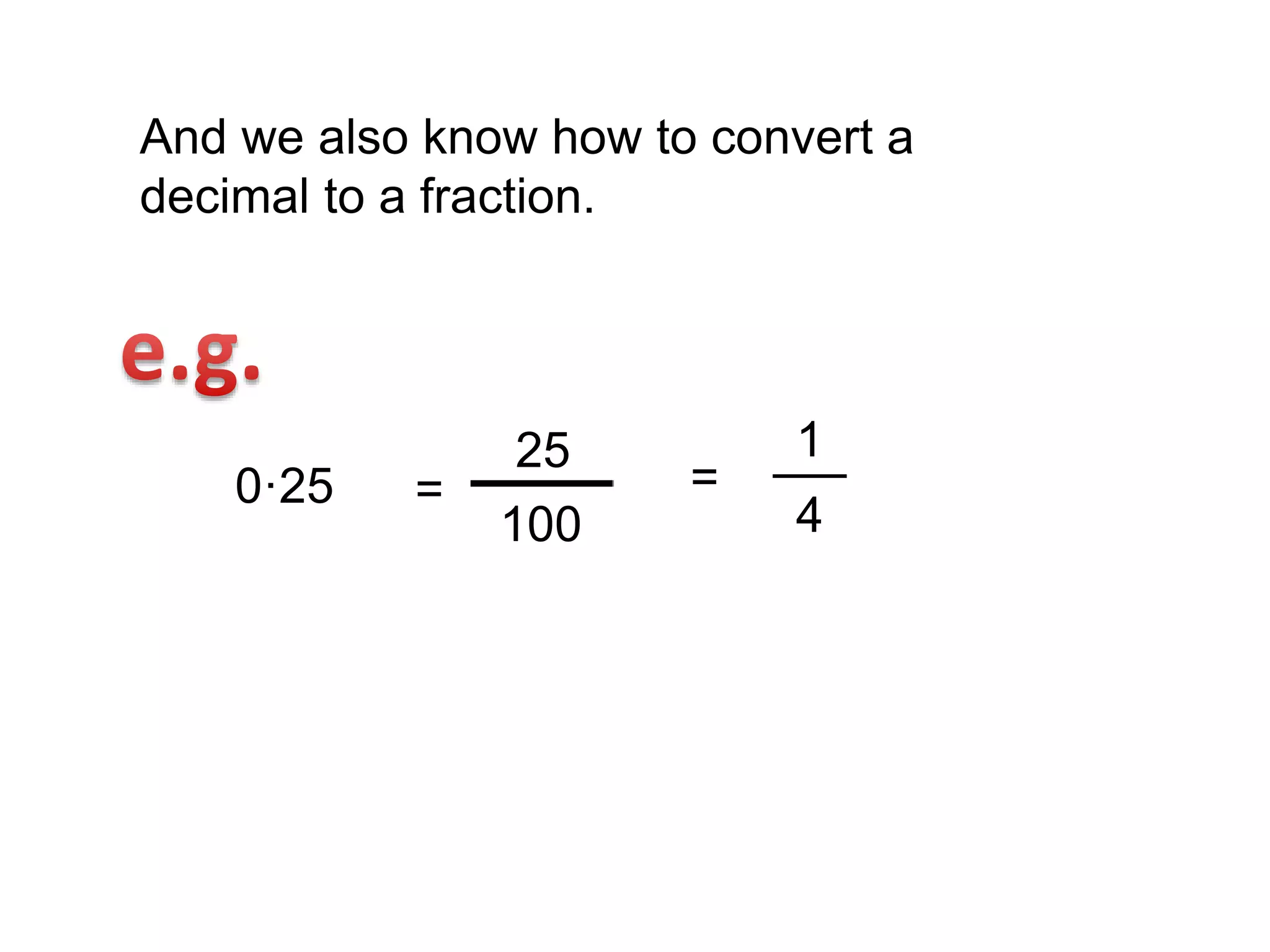This document explains how to convert repeating decimals to fractions. It shows that the denominator is determined by multiplying the decimal by the appropriate power of 10 based on the number of repeating digits, then subtracting the original decimal from both sides and solving for the fraction. Examples are provided converting 0.333..., 0.424242..., and 0.348348... to fractions.

1. *

2. We all ready know how to calculate a
fraction to a decimal.
We divide the ‘numerator’ by the ‘denominator’
___
4
numerator
denominator
1

3. 4 ) 1
0·
0
2
2
remainder
0

4. 4 ) 1
0·
0
2
2
remainder
0
5
remainder 0 end
ans.

5. And we also know how to convert a
decimal to a fraction.
0·25 =
25
100
=
1
4

7. Lets look at an example:
The most obvious one to start with is 0.333…..
or 0.3
.
You remember how we converted ⅓ to a decimal.
3)1
But how do we convert 0.333…. back to
a fraction?

8. We have learned that when we convert
non-repeating decimals (sometimes
called ‘zero repeating decimals’) to
fractions, the denominator is always a
power of 10.
i.e. 101, 102, 103 …… etc.
But when we convert repeating decimals
the denominator cannot be 10.
So let’s look at how we calculate the
denominator.

9. Let’s look at 0.333……
First we start by stating: Let n = 0.333….
n = 0.333….
Next because there is only 1 repeating
number we multiply each side of the
equation by 10. So -
10n = 3.333……..
n x 10 = 0.333…. x 10

10. Next we subtract ‘n’ from each side of the
equation.
10n – n = 3.333…. - n
(remember n = 0.333… )
9n = 3
n = 3
9
= 1
3
ans

11. Now, let’s see what happens when
we have 2 repeating decimals.
Let’s look at 0.424242…….
(or it may be written as 0.42)
. .
Again we state: Let n = 0.424242…..
This time because we have 2 repeating
decimals we multiply each side of the
equation by 100.

12. n x 100 = 0.424242…… x 100
So we have:
100n = 42.424242…..
As before we now subtract ‘n’ from each
side of the equation.
100n – n = 42.424242…. - n
(remember n = 0.424242… )
99n = 42
n = 42
99
= 14
33
ans

13. Now, let’s see what happens when
we have 3 repeating decimals.
Let’s look at 0.348348…….
(or it may be written as 0.348)
. .
Again we state: Let n = 0.348348…..
This time because we have 3 repeating
decimals we multiply each side of the
equation by 1000.

14. n x 1000 = 0.348348… x 1000
So we have:
1000n = 348.348348…..
As before we now subtract ‘n’ from each
side of the equation.
1000n – n = 348.348348…. - n
(remember: n = 0.348348… )
999n = 348
n = 348
999
= 116
333
ans