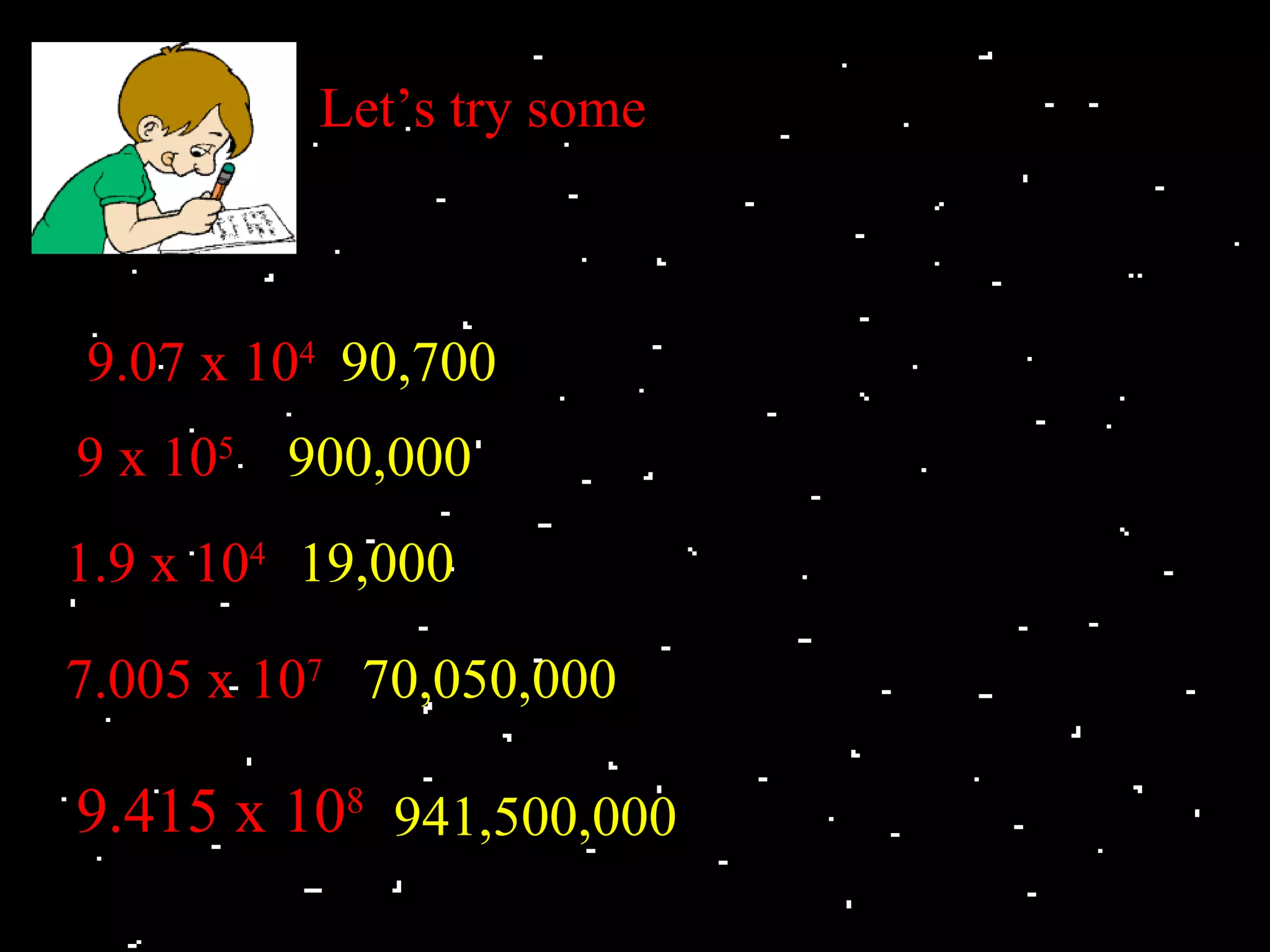
Scientific notation is a way to write very large or small numbers in a more compact form. To write a number in scientific notation, you express it as the product of two factors: a decimal number greater than or equal to 1 but less than 10, and a power of 10. For example, 93,000,000 would be written as 9.3 x 107. The power of 10 indicates how many places the decimal is moved. Very small decimals between 0 and 1 use a negative power of 10. For example, 0.00064 would be written as 6.4 x 10-4. Scientific notation makes large and small numbers easier to work with

2. Finish these equations
7000 = 7 x 10n 3
600,000 = 6 x 10n 5
30,000,000 = 3 x 10n 7
1.47 x 100 = 147
82 x 10,000 = 820,000
0.0629 x 1000 = 62.9

3. Scientists use easy ways to write large numbers.
This easy way is more compact & more useful.
This compact, useful method is called
To write a number in Scientific Notation, express it as a
product of two factors
There are 2 criteria for writing a number in Scientific
Notation:

4. Criteria:
•One factor is a number GREATER than or EQUAL to 1, but
LESS than 10. (This will usually be a decimal)
b. The other factor is a POSITIVE POWER of 10.
Let’s look at an example:
93,000,000 Notice that the
decimal point is
moved until it
reaches a
number greater
than 1, but less
than 10.

5. How many times was the decimal point moved to the left?
That answer is your exponent.
93,000,000 in Scientific Notation is: 9.3 x 107
Steps:
1. Move the decimal point to the LEFT until you
get to a number greater than or equal to 1, but less
than 10.
2. Count the number of places moved- that is the
power of 10.

6. Another example:
185,000 1.85 x 105
Let’s try some:
120,000 1.2 x 105
4,064,000 4.064 x 106
25,000 2.5 x 104
714,500 7.145 x 105
156,000,000 1.56 x 108

7. How would you reverse Scientific Notation (write in
standard form)?
Do the OPPOSITE.
2.Move the decimal point the number of places as the
exponent in the Power of 10 to the RIGHT.
2. Add 0’s as place fillers.
3.6 x 103 3,600

8. Let’s try some
9.07 x 104 90,700
9 x 105 900,000
1.9 x 104 19,000
7.005 x 107 70,050,000
9.415 x 108 941,500,000

9. Scientific Notation can also be used to rename
large decimals that are between 0 & 1
These numbers will use negative exponents for their
powers of 10.
Follow these rules:
Let’s look at an example:
3.First factor is greater than
1, but less than 10.
0.00064=
2. Second factor is a power
6.4 x 10-4 of 10 with a negative
exponent. The exponent
depends on how many times
you moved the decimal to the
RIGHT.

10. Here’s another example:
0.0815 = 8.15 x 10-2
You try some:
0.015 = 1.5 x 10-2
0.0000086= 8.6 x 10-6
0.000124= 1.24 x 10-4
0.0069= 6.9 x 10-3

11. 0.00000079 = 7.9 x 10-7
0.0000716 = 7.16 x 10-5
0.0045 = 4.5 x 10-3
It is now your turn to explain how to write numbers in
scientific notation. Explain the process of scientific
notation to the person next to you. Explain it using whole
numbers & decimal between 0 & 1. Pretend that your
partner does not understand this process, so explain it
well & with examples!