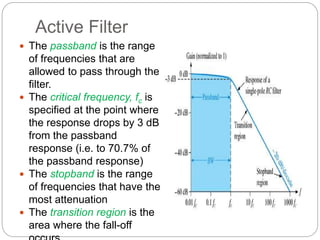
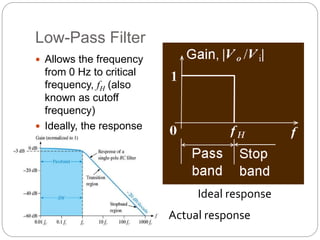
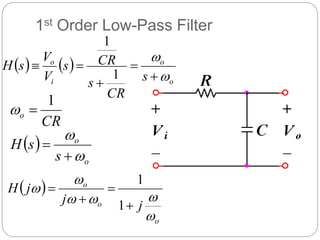
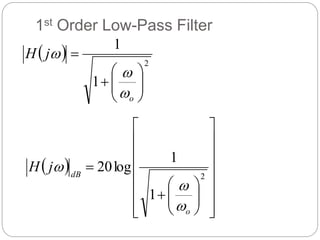
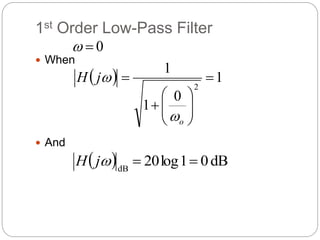
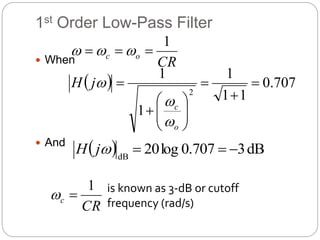
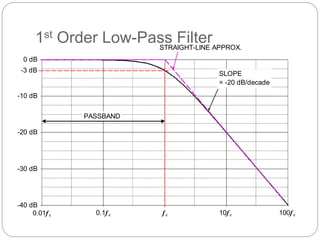
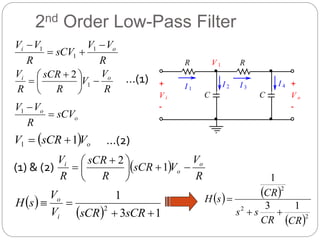
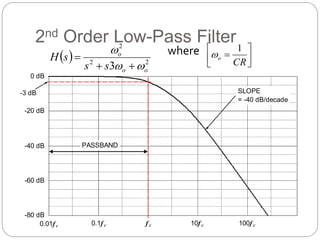
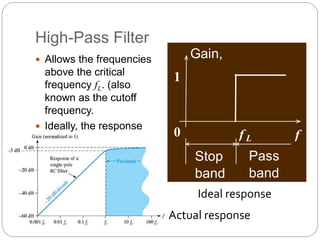
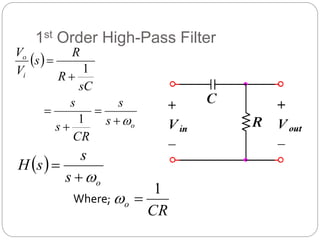
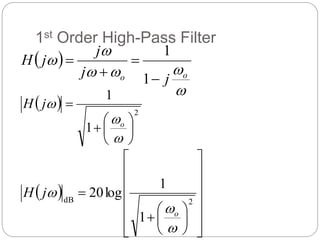
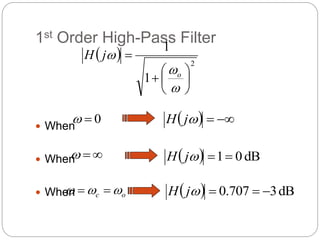
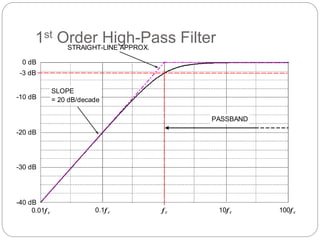
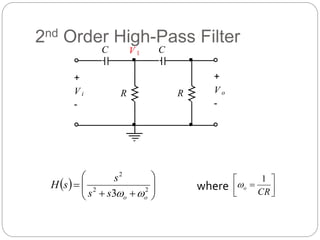
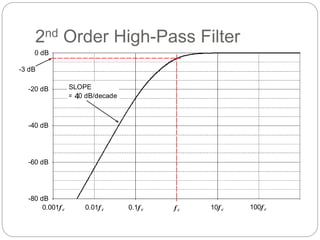
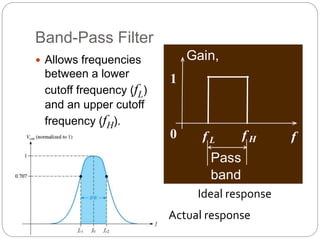
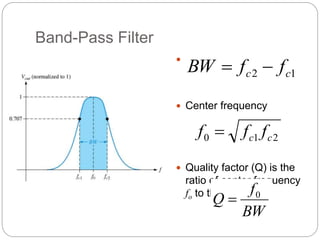
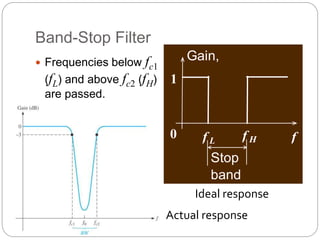
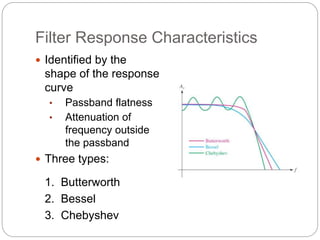
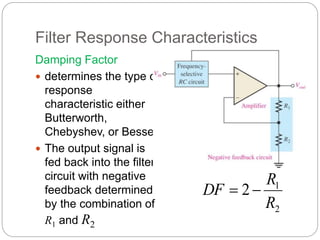
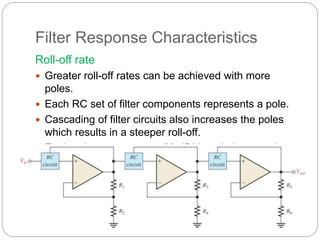
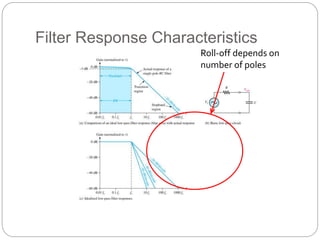
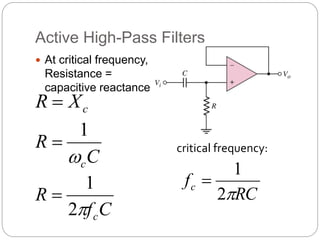
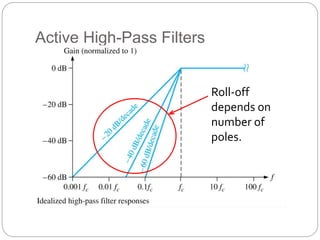
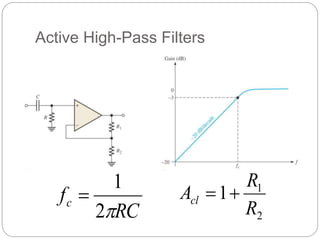
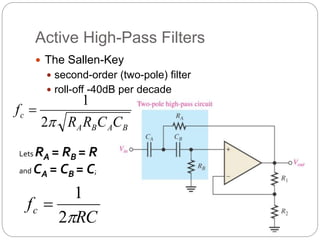
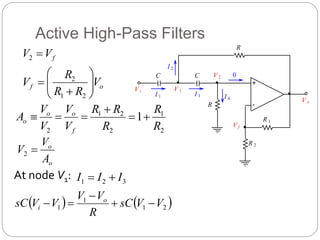
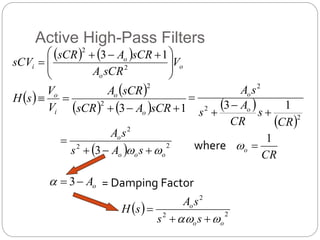
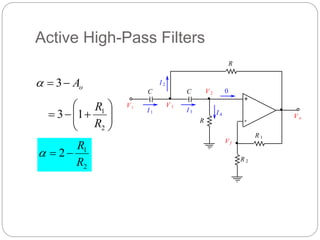
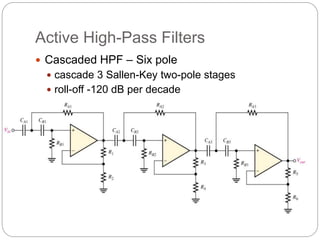
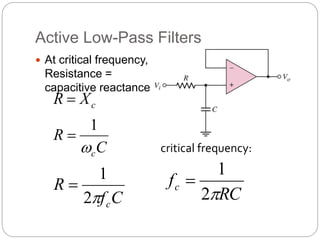
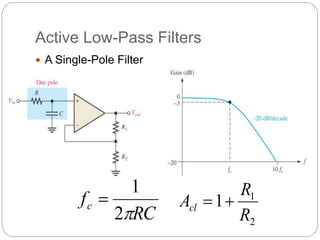
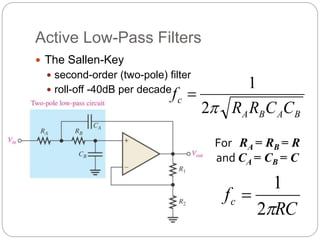
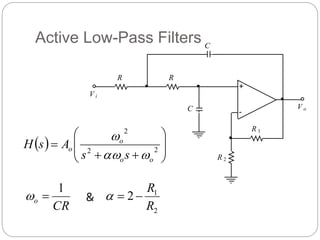
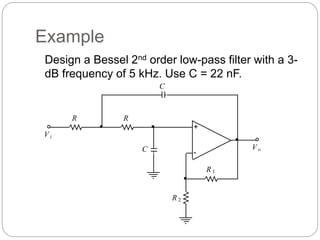
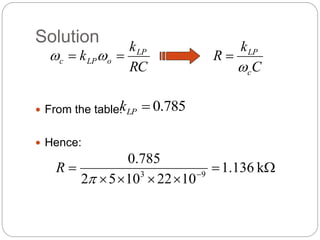
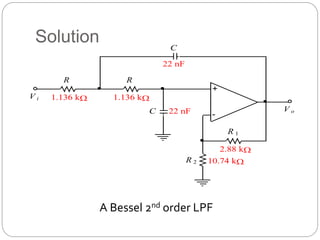
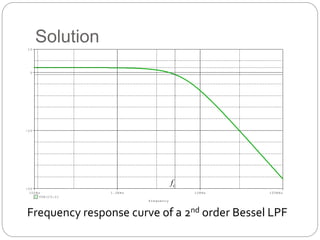
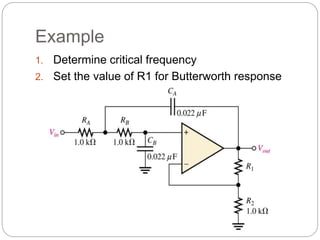
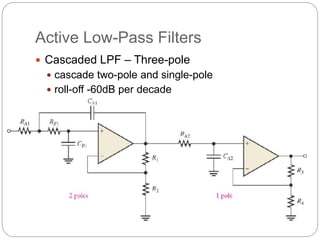
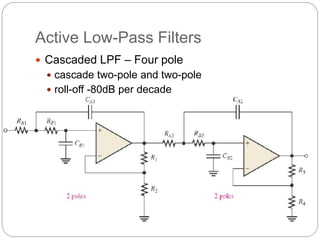
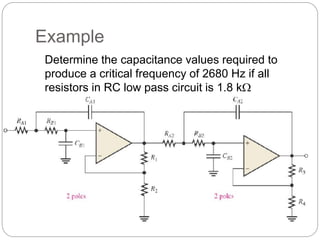
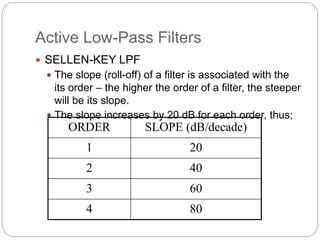
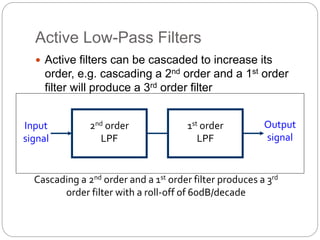
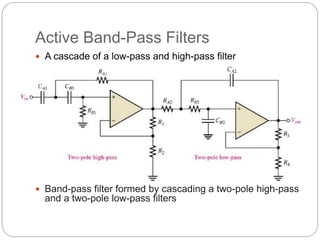
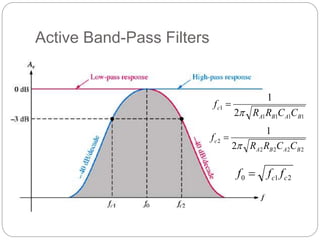
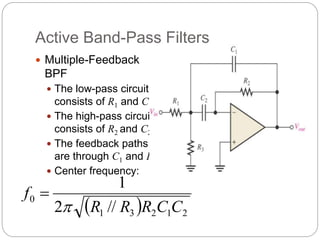
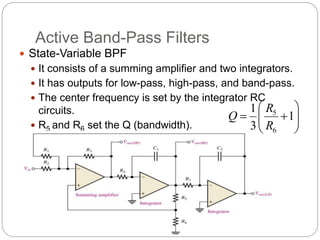
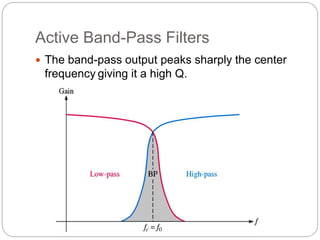
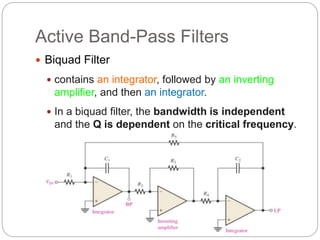
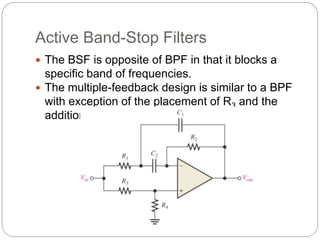
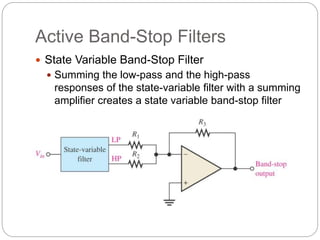
This document outlines different types of active filters including low-pass, high-pass, band-pass, and band-stop filters. It describes the advantages of active filters over passive filters, such as the ability to provide gain and avoid loading problems. The key characteristics of different order filters, such as the 1st and 2nd order low-pass and high-pass filters, are presented. Finally, it discusses filter response characteristics such as Butterworth, Bessel, and Chebyshev responses as well as concepts like critical frequency and roll-off rate.

1. EMT 359/3 – Analog Electronic II
Chapter 5:
Active Filters

2. Outlines
1. Introduction
2. Advantages of Active Filters over Passive Filters
3. Types of filter
4. Filter Response Characteristic
5. Active Low-Pass Filter
6. Active High-Pass Filter
7. Active Band-Pass Filter
8. Active Band-Stop Filter
9. Summary

3. Introduction
 Filters are circuits that are capable of passing signals
within a band of frequencies while rejecting or
blocking signals of frequencies outside this band.
 This property of filters is also called “frequency
selectivity”.
 Passive filters - built using components such as
resistors, capacitors and inductors.
 Active filters - employ transistors or op-amps in
addition to resistors and capacitors.
 Active filters are mainly used in communication and
signal processing circuits.
 They are also employed in a wide range of
applications such as entertainment, medical
electronics, etc.

4. Advantages of Active Filters over Passive
Filters
1. Active filters can be designed to provide
required gain, and hence no attenuation as in
the case of passive filters.
2. No loading problem, because of high input
resistance and low output resistance of op-amp.
3. Active Filters are cost effective as a wide variety
of economical op-amps are available.

5. Active Filter
 There are 4 basic categories of active filters:
 Low-Pass filters
 High-Pass filters
 Band-Pass filters
 Band-Stop filters
 Each of these filters can be built by using op-amp
or transistor as the active element combined with
RC, RL or RLC circuit as the passive elements.

6. Active Filter
 The passband is the range
of frequencies that are
allowed to pass through the
filter.
 The critical frequency, fc is
specified at the point where
the response drops by 3 dB
from the passband
response (i.e. to 70.7% of
the passband response)
 The stopband is the range
of frequencies that have the
most attenuation
 The transition region is the
area where the fall-off

7. Low-Pass Filter
 Allows the frequency
from 0 Hz to critical
frequency, fH (also
known as cutoff
frequency)
 Ideally, the response
drops abruptly at the
critical frequency fH
Ideal response
Actual response

8. 1st Order Low-Pass Filter
   
o
o
i
o
s
CR
s
CR
s
V
V
s
H







1
1
 
o
o
s
s
H




CR
o
1


 
o
o
o
j
j
j
H










1
1

9. 1st Order Low-Pass Filter
 


























2
1
1
log
20
o
dB
j
H



  2
1
1










o
j
H




10. 1st Order Low-Pass Filter
 When
 And
  1
0
1
1
2











o
j
H


0


  dB
0
1
log
20
dB



j
H

11. 1st Order Low-Pass Filter
 When
 And
  707
.
0
1
1
1
1
1
2













o
c
j
H



CR
o
c
1


 


  dB
3
707
.
0
log
20
dB




j
H
CR
c
1

 is known as 3-dB or cutoff
frequency (rad/s)

12. 1st Order Low-Pass Filter
f c
0 dB
-10 dB
-20 dB
-30 dB
-40 dB
-3 dB
PASSBAND
SLOPE
= -20 dB/decade
0.1f c
0.01f c 10f c 100f c
STRAIGHT-LINE APPROX.

13. 2nd Order Low-Pass Filter
R
C
+
V i
-
+
V o
-
R
C
V 1
I 1
I 2 I 3 I 4
R
V
V
sCV
R
V
V o
i 


 1
1
1
R
V
V
R
sCR
R
V o
i






 
 1
2
o
o
sCV
R
V
V


1
…(1)
  o
V
sCR
V 1
1 
 …(2)
(1) & (2)  
R
V
V
sCR
R
sCR
R
V o
o
i







 
 1
2
 
  1
3
1
2




sCR
sCR
V
V
s
H
i
o    
 2
2
2
1
3
1
CR
CR
s
s
CR
s
H




14. 2nd Order Low-Pass Filter
  2
2
2
3 o
o
o
s
s
s
H





 






CR
o
1

where
f c
0.1f c
0.01f c 10f c 100f c
0 dB
-20 dB
-40 dB
-60 dB
-80 dB
-3 dB SLOPE
= -40 dB/decade
PASSBAND

15. High-Pass Filter
 Allows the frequencies
above the critical
frequency fL. (also
known as the cutoff
frequency.
 Ideally, the response
rises abruptly at the
critical frequency.
0
1
f L f
Gain,
Pass
band
Stop
band
Ideal response
Actual response

16. 1st Order High-Pass Filter
 
o
i
o
s
s
CR
s
s
sC
R
R
s
V
V







1
1
 
o
s
s
s
H



CR
o
1


Where;

17. 1st Order High-Pass Filter
 






o
o j
j
j
j
H




1
1
  2
1
1











o
j
H
 






















2
dB
1
1
log
20



o
j
H

18. 1st Order High-Pass Filter
 When
 When
 When
  2
1
1











o
j
H
0

   


j
H


   dB
0
1


j
H
o
c 

 
   dB
3
707
.
0 



j
H

19. 1st Order High-Pass Filter
f c
0.1f c
0.01f c 10f c 100f c
0 dB
-10 dB
-20 dB
-30 dB
-40 dB
-3 dB
SLOPE
= 20 dB/decade
PASSBAND
STRAIGHT-LINE APPROX.

20. 2nd Order High-Pass Filter
+
V i
-
+
V o
-
R R
V 1
C C
  









 2
2
2
3 o
o
s
s
s
s
H

 






CR
o
1

where

21. 2nd Order High-Pass Filter
f c
0.1f c
0.01f c 10f c 100f c
0.001f c
0 dB
-20 dB
-40 dB
-60 dB
-80 dB
-3 dB
SLOPE
= 20 dB/decade
4

22. 1st & 2nd Order Filter
Low-Pass Filter (LPF) High-Pass Filter






 
c
s
s
s
H



 
c
c
s
s
H




 
o
j
j
H





1
1
 



o
j
j
H


1
1
  2
2
2
3 o
o
o
s
s
s
H





   









 2
2
2
3 o
o
s
s
s
s
H



23. Band-Pass Filter
 Allows frequencies
between a lower
cutoff frequency (fL)
and an upper cutoff
frequency (fH).
0
1
f L f
Gain,
Pass
band
f H
Ideal response
Actual response

24. Band-Pass Filter
 Bandwidth (BW)
 Center frequency
 Quality factor (Q) is the
ratio of center frequency
fo to the BW
1
2 c
c f
f
BW 

BW
f
Q 0

2
1
0 c
c f
f
f 

25. Band-Stop Filter
 Frequencies below fc1
(fL) and above fc2 (fH)
are passed.
0
1
f L f
Gain,
Stop
band
f H
Ideal response
Actual response

26. Filter Response Characteristics
 Identified by the
shape of the response
curve
• Passband flatness
• Attenuation of
frequency outside
the passband
 Three types:
1. Butterworth
2. Bessel
3. Chebyshev

27. Filter Response Characteristics
1. Butterworth
 Amplitude response is very flat in passband.
 The roll-off rate -20 dB per decade (per filter order).
 normally used when all frequencies in the passband
must have the same gain.
2. Chebyshev
 overshoot or ripples in the passband.
 The roll-off rate greater than –20 dB.
 can be implemented with fewer poles and less complex
circuitry for a given roll-off rate.
3. Bessel
 Linear phase response.
 Ideal for filtering pulse waveforms.

28. Filter Response Characteristics
Damping Factor
 determines the type of
response
characteristic either
Butterworth,
Chebyshev, or Bessel.
 The output signal is
fed back into the filter
circuit with negative
feedback determined
by the combination of
R1 and R2
2
1
2
R
R
DF 


29. Filter Response Characteristics
Critical Frequency
 The critical frequency, fc
is determined by the
values of R and C in the
frequency-selective RC
circuit.
 For a single-pole (first-
order) filter, the critical
frequency is:
 The above formula can
be used for both low-
pass and high-pass
filters
RC
fc

2
1


30. Filter Response Characteristics
Roll-off rate
 Greater roll-off rates can be achieved with more
poles.
 Each RC set of filter components represents a pole.
 Cascading of filter circuits also increases the poles
which results in a steeper roll-off.
 Each pole represents a –20 dB/decade increase in
roll-off

31. Filter Response Characteristics
Roll-off depends on
number of poles

32. Active High-Pass Filters
 At critical frequency,
Resistance =
capacitive reactance
c
X
R 
C
f
R
c

2
1

C
R
c

1
 critical frequency:
RC
fc

2
1


33. Active High-Pass Filters
Roll-off
depends on
number of
poles.

34. Active High-Pass Filters
 A Single-Pole Filter
RC
fc

2
1

2
1
1
R
R
Acl 


35. Active High-Pass Filters
 The Sallen-Key
 second-order (two-pole) filter
 roll-off -40dB per decade
RC
fc

2
1

Lets RA = RB = R
and CA = CB = C;
B
A
B
A
c
C
C
R
R
f

2
1


36. Active High-Pass Filters
C C
R
R
R 1
R 2
+
-
V o
V i
V f
V 1
V 2
I 1
I 2
I 3 I 4
0
f
V
V 
2
o
f V
R
R
R
V 









2
1
2
2
1
2
2
1
2
1
R
R
R
R
R
V
V
V
V
A
f
o
o
o 





o
o
A
V
V 
2
3
2
1 I
I
I 

   
2
1
1
1 V
V
sC
R
V
V
V
V
sC o
i 




At node V1:

37. Active High-Pass Filters
  












o
o
o
i
A
V
V
sC
R
V
V
V
V
sC 1
1
1 ……(1)
4
3 I
I 
 
R
V
V
V
sC 2
2
1 

R
A
V
A
V
V
sC
o
o
o
o










1
sCR
A
V
A
V
V
o
o
o
o


1 ……(2)
At node V2:
(2) in (1): o
o
o
o
o
i V
A
sC
R
V
sCR
A
A
C
s
R
sCV 


























1
1
1
2
1

38. Active High-Pass Filters
   
    1
3
2
2





sCR
A
sCR
sCR
A
V
V
s
H
o
o
i
o
   
o
o
o
i V
sCR
A
sCR
A
sCR
sCV 






 


 2
2
1
3
 
 2
2
2
1
3
CR
s
CR
A
s
s
A
o
o




  2
2
2
3 o
o
o
o
s
A
s
s
A

 



CR
o
1


where
o
A

 3

  2
2
2
o
o
o
s
s
s
A
s
H

 


= Damping Factor

39. Active High-Pass Filters
C C
R
R
R 1
R 2
+
-
V o
V i
V f
V 1
V 2
I 1
I 2
I 3 I 4
0
o
A

 3












2
1
1
3
R
R
2
1
2
R
R




40. Active High-Pass Filters
 Cascaded HPF – Six pole
 cascade 3 Sallen-Key two-pole stages
 roll-off -120 dB per decade

41. Active Low-Pass Filters
 At critical frequency,
Resistance =
capacitive reactance
c
X
R 
C
f
R
c

2
1

C
R
c

1

critical frequency:
RC
fc

2
1


42. Active Low-Pass Filters
 A Single-Pole Filter
2
1
1
R
R
Acl 

RC
fc

2
1


43. Active Low-Pass Filters
 The Sallen-Key
 second-order (two-pole) filter
 roll-off -40dB per decade
RC
fc

2
1

For RA = RB = R
and CA = CB = C
B
A
B
A
c
C
C
R
R
f

2
1


44. Active Low-Pass Filters
C
C
R R
R 1
R 2
+
-
V i
V o
  









 2
2
2
o
o
o
o
s
s
A
s
H



CR
o
1


2
1
2
R
R



&

45. Active Low-Pass Filters
 The 3-dB frequency c is related to o by a
factor known as the FREQUENCY
CORRECTION FACTOR (kLP), thus;
 Parameter table for Sellen-Key 2nd order LPF
RC
k
k LP
o
LP
c 
 

Type of response  kLP
Bessel 1.732 0.785
Butterworth 1.414 1
Chebyshev (1 dB) 1.054 1.238
Chebyshev (2 dB) 0.886 1.333
Chebyshev (3 dB) 0.766 1.390

46. Example
Design a Bessel 2nd order low-pass filter with a 3-
dB frequency of 5 kHz. Use C = 22 nF.
C
C
R R
R 1
R 2
+
-
V i
V o

47. Solution
 From the table:
 Hence:
RC
k
k LP
o
LP
c 
 

C
k
R
c
LP


785
.
0

LP
k






 
k
136
.
1
10
22
10
5
2
785
.
0
9
3

R

48. Solution
 In order to minimize the offset error, we have to
meet the following condition:
 Or;
 And:
R
R
R 2
// 2
1 




k
27
.
2
2
2
1
2
1
R
R
R
R
R
2
1
2
R
R



From the parameter table; 732
.
1



49. Solution
268
.
0
2
2
1


 
R
R
2
1 268
.
0 R
R  


k
27
.
2
2
1
2
1
R
R
R
R



k
27
.
2
268
.
0
268
.
0
2
2
2
2
R
R
R



 k
10.74
268
.
0
27
.
2
268
.
1
2
R




 k
88
.
2
74
.
10
268
.
0
268
.
0 2
1 R
R

50. Solution
C
C
R R
R 1
R 2
+
-
V i
V o
1.136 k 1.136 k
22 nF
22 nF
2.88 k
10.74 k
A Bessel 2nd order LPF

51. Solution
Frequency response curve of a 2nd order Bessel LPF
Frequency
100Hz 1.0KHz 10KHz 100KHz
VDB(C5:2)
-50
-25
0
10
fc

52. Example
1. Determine critical frequency
2. Set the value of R1 for Butterworth response

53. Solution
1. Critical frequency
2. Butterworth response, R1/R2 = 0.586
kHz
23
.
7
2
1


RC
fc

2
1 586
.
0 R
R 
kΩ
586
1 
R

54. Active Low-Pass Filters
 Cascaded LPF – Three-pole
 cascade two-pole and single-pole
 roll-off -60dB per decade

55. Active Low-Pass Filters
 Cascaded LPF – Four pole
 cascade two-pole and two-pole
 roll-off -80dB per decade

56. Example
Determine the capacitance values required to
produce a critical frequency of 2680 Hz if all
resistors in RC low pass circuit is 1.8 k

57. Solution
RC
fc

2
1

μF
033
.
0
2
1


R
f
C
c

μF
033
.
0
2
2
1
1 


 B
A
B
A C
C
C
C

58. Active Low-Pass Filters
 SELLEN-KEY LPF
 The slope (roll-off) of a filter is associated with the
its order – the higher the order of a filter, the steeper
will be its slope.
 The slope increases by 20 dB for each order, thus;
ORDER SLOPE (dB/decade)
1 20
2 40
3 60
4 80

59. Active Low-Pass Filters
 Active filters can be cascaded to increase its
order, e.g. cascading a 2nd order and a 1st order
filter will produce a 3rd order filter
2nd order
LPF
1st order
LPF
Input
signal
Output
signal
Cascading a 2nd order and a 1st order filter produces a 3rd
order filter with a roll-off of 60dB/decade

60. Active Band-Pass Filters
 A cascade of a low-pass and high-pass filter
 Band-pass filter formed by cascading a two-pole high-pass
and a two-pole low-pass filters

61. Active Band-Pass Filters
2
1
0 c
c f
f
f 
1
1
1
1
1
2
1
B
A
B
A
c
C
C
R
R
f


2
2
2
2
2
2
1
B
A
B
A
c
C
C
R
R
f



62. Active Band-Pass Filters
 Multiple-Feedback
BPF
 The low-pass circuit
consists of R1 and C1.
 The high-pass circuit
consists of R2 and C2.
 The feedback paths
are through C1 and R2.
 Center frequency:
  2
1
2
3
1
0
//
2
1
C
C
R
R
R
f



63. Active Band-Pass Filters
 Multiple-Feedback BPF
 For C1 = C2 = C, the resistor values can be
obtained using the following formulas:
 The maximum gain, Ao occurs at the center
frequency.
o
oCA
f
Q
R

2
1 
C
f
Q
R
o


2
)
2
(
2 2
3
o
o A
Q
C
f
Q
R




64. Active Band-Pass Filters
 State-Variable BPF
 It consists of a summing amplifier and two integrators.
 It has outputs for low-pass, high-pass, and band-pass.
 The center frequency is set by the integrator RC
circuits.
 R5 and R6 set the Q (bandwidth). 








 1
3
1
6
5
R
R
Q

65. Active Band-Pass Filters
 The band-pass output peaks sharply the center
frequency giving it a high Q.

66. Active Band-Pass Filters
 Biquad Filter
 contains an integrator, followed by an inverting
amplifier, and then an integrator.
 In a biquad filter, the bandwidth is independent
and the Q is dependent on the critical frequency.

67. Active Band-Stop Filters
 The BSF is opposite of BPF in that it blocks a
specific band of frequencies.
 The multiple-feedback design is similar to a BPF
with exception of the placement of R3 and the
addition of R4

68. Active Band-Stop Filters
 State Variable Band-Stop Filter
 Summing the low-pass and the high-pass
responses of the state-variable filter with a summing
amplifier creates a state variable band-stop filter

69. Summary
 The bandwidth of a low-pass filter is the same as
the upper critical frequency.
 The bandwidth of a high-pass filter extends from
the lower critical frequency up to the inherent
limits of the circuit.
 The band-pass passes frequencies between the
lower critical frequency and the upper critical
frequency.
 A band-stop filter rejects frequencies within the
upper critical frequency and upper critical
frequency.

70. Summary
 The Butterworth filter response is very flat and
has a roll-off rate of –20 dB.
 The Chebyshev filter response has ripples and
overshoot in the passband but can have roll-off
rates greater than –20 dB.
 The Bessel response exhibits a linear phase
characteristic, and filters with the Bessel
response are better for filtering pulse waveforms.

71. Summary
 A filter pole consists of one RC circuit. Each pole
doubles the roll-off rate.
 The Q of a filter indicates a band-pass filter’s
selectivity. The higher the Q the narrower the
bandwidth.
 The damping factor determines the filter response
characteristic.