hh

1. Graph Traversal
• BFS (Breadth First Search)
– Start from a vertex, visit all the reachable
vertices in a breadth first manner
– Uses Queue for non-recursive implementation
• DFS (Depth First Search)
– Start from a vertex, visit all the reachable
vertices in a depth first manner
– Uses Stack for non-recursive implementation

2. Depth-First Search
dfs (G, A) //A is starting node

3. DFS: Start with start Node 5
0
7
1
5
4
3
2
6

4. DFS: Start with Node 5
0
7
1
5
4
3
2
6
5
Push 5

5. DFS: Start with Node 5
0
7
1
5
4
3
2
6
Visited: 5
Pop/Visit 5

6. DFS: Start with Node 5
0
7
1
5
4
3
2
6
Visited: 5
1
2
Push 2, Push 1

7. DFS: Start with Node 5
0
7
1
5
4
3
2
6
Visited: 5 1
2
Pop/Visit 1

8. DFS: Start with Node 5
7
1
5
4
3
2
6
Visited: 5 1
0
4
2
Push 4, Push 0
0

9. DFS: Start with Node 5
7
1
5
4
3
2
6
Visited: 5 1 0
4
2
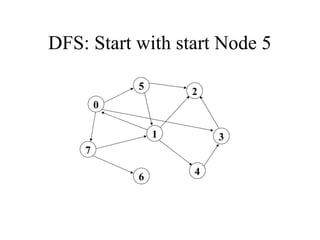
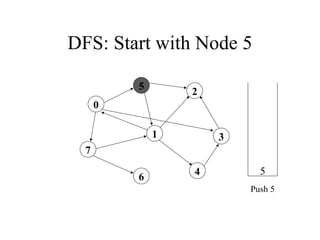
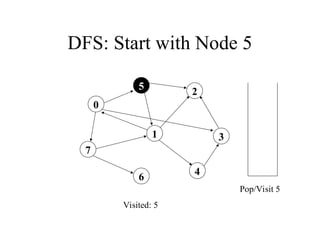
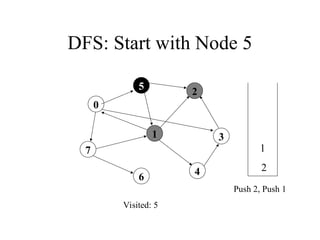
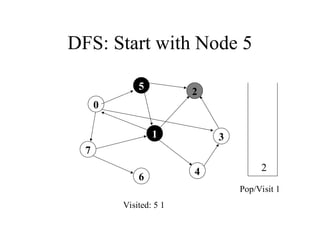
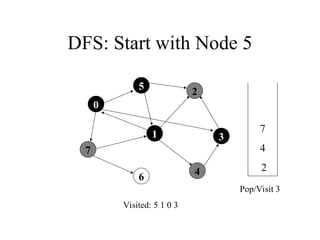
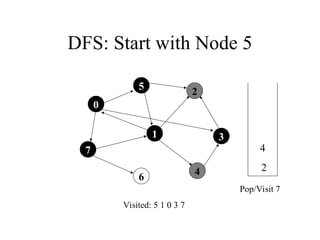
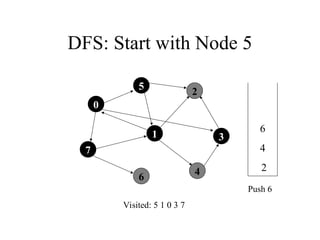
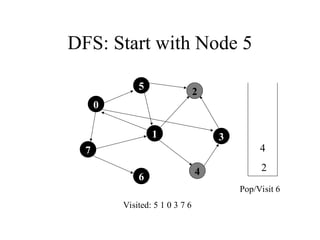
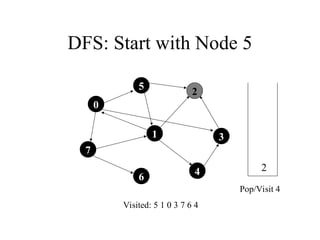
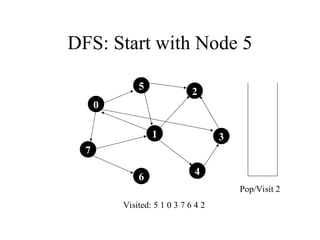
Pop/Visit 0
0

10. DFS: Start with Node 5
7
1
5
4
3
2
6
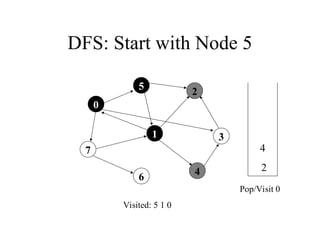
Visited: 5 1 0
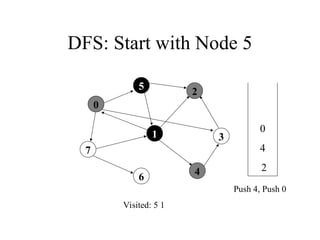
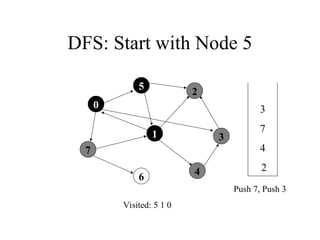
3
7
4
2
Push 7, Push 3
0

11. DFS: Start with Node 5
7
1
5
4
3
2
6
Visited: 5 1 0 3
7
4
2
Pop/Visit 3
0

12. DFS: Start with Node 5
7
1
5
4
3
2
6
Visited: 5 1 0 3 7
4
2
Pop/Visit 7
0

13. DFS: Start with Node 5
7
1
5
4
3
2
6
Visited: 5 1 0 3 7
6
4
2
Push 6
0

14. DFS: Start with Node 5
7
1
5
4
3
2
6
Visited: 5 1 0 3 7 6
4
2
Pop/Visit 6
0

15. DFS: Start with Node 5
7
1
5
4
3
2
6
Visited: 5 1 0 3 7 6 4
2
Pop/Visit 4
0

16. DFS: Start with Node 5
7
1
5
4
3
2
6
Visited: 5 1 0 3 7 6 4 2
Pop/Visit 2
0

17. Breadth-first Search
bfs (G, A) //A is the start node

18. BFS: Start with Node 5
7
1
5
4
3
2
6
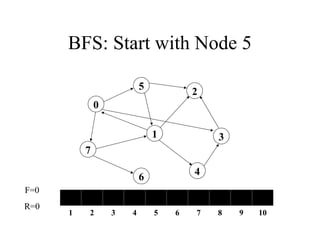
F=0
R=0
0
1 2 3 4 5 6 7 8 9 10

19. BFS: Start with Node 5
7
1
5
4
3
2
6
Visited:
0
5
1 2 3 4 5 6 7 8 9 10
F=1
R=1
Enqueue 5

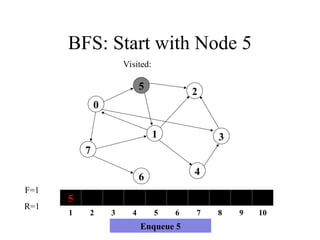
20. BFS: Start with Node 5
7
1
5
4
3
2
6
0
1 2 3 4 5 6 7 8 9 10
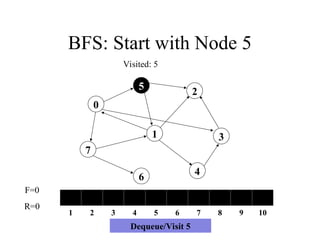
F=0
R=0
Dequeue/Visit 5
Visited: 5

21. BFS: Start with Node 5
7
1
5
4
3
2
6
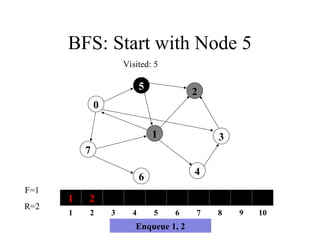
0
1 2
1 2 3 4 5 6 7 8 9 10
F=1
R=2
Visited: 5
Enqueue 1, 2

22. BFS: Start with Node 5
7
1
5
4
3
2
6
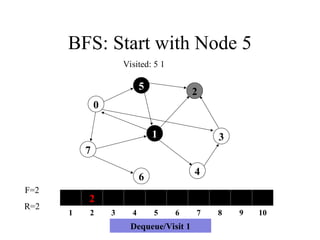
0
2
1 2 3 4 5 6 7 8 9 10
F=2
R=2
Visited: 5 1
Dequeue/Visit 1

23. BFS: Start with Node 5
7
1
5
4
3
2
6
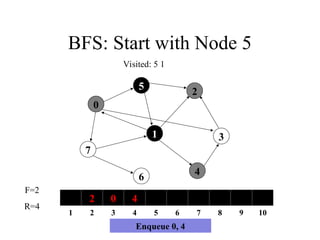
0
2 0 4
1 2 3 4 5 6 7 8 9 10
F=2
R=4
Visited: 5 1
Enqueue 0, 4

24. BFS: Start with Node 5
7
1
5
4
3
2
6
0
0 4
1 2 3 4 5 6 7 8 9 10
F=3
R=4
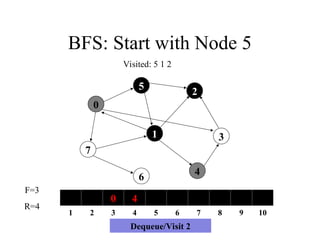
Visited: 5 1 2
Dequeue/Visit 2

25. BFS: Start with Node 5
7
1
5
4
3
2
6
0
4
1 2 3 4 5 6 7 8 9 10
F=4
R=4
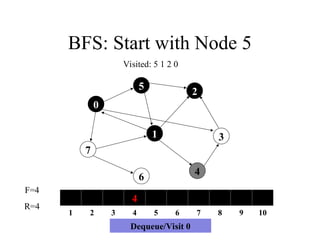
Visited: 5 1 2 0
Dequeue/Visit 0

26. BFS: Start with Node 5
7
1
5
4
3
2
6
0
4 3 7
1 2 3 4 5 6 7 8 9 10
F=4
R=6
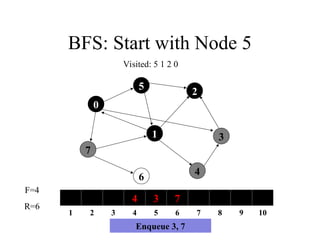
Visited: 5 1 2 0
Enqueue 3, 7

27. BFS: Start with Node 5
7
1
5
4
3
2
6
0
3 7
1 2 3 4 5 6 7 8 9 10
F=5
R=6
Visited: 5 1 2 0 4
Dequeue/Visit 4

28. BFS: Start with Node 5
7
1
5
4
3
2
6
0
7
1 2 3 4 5 6 7 8 9 10
F=6
R=6
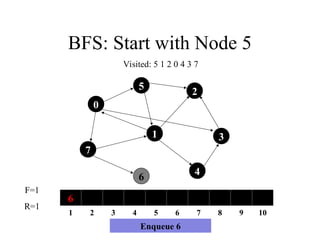
Visited: 5 1 2 0 4 3
Dequeue/Visit 3

29. BFS: Start with Node 5
7
1
5
4
3
2
6
0
1 2 3 4 5 6 7 8 9 10
F=0
R=0
Visited: 5 1 2 0 4 3 7
Dequeue/Visit 7

30. BFS: Start with Node 5
7
1
5
4
3
2
6
0
6
1 2 3 4 5 6 7 8 9 10
F=1
R=1
Visited: 5 1 2 0 4 3 7
Enqueue 6

31. BFS: Start with Node 5
7
1
5
4
3
2
6
0
1 2 3 4 5 6 7 8 9 10
F=0
R=0
Visited: 5 1 2 0 4 3 7 6
Dequeue/Visit 6