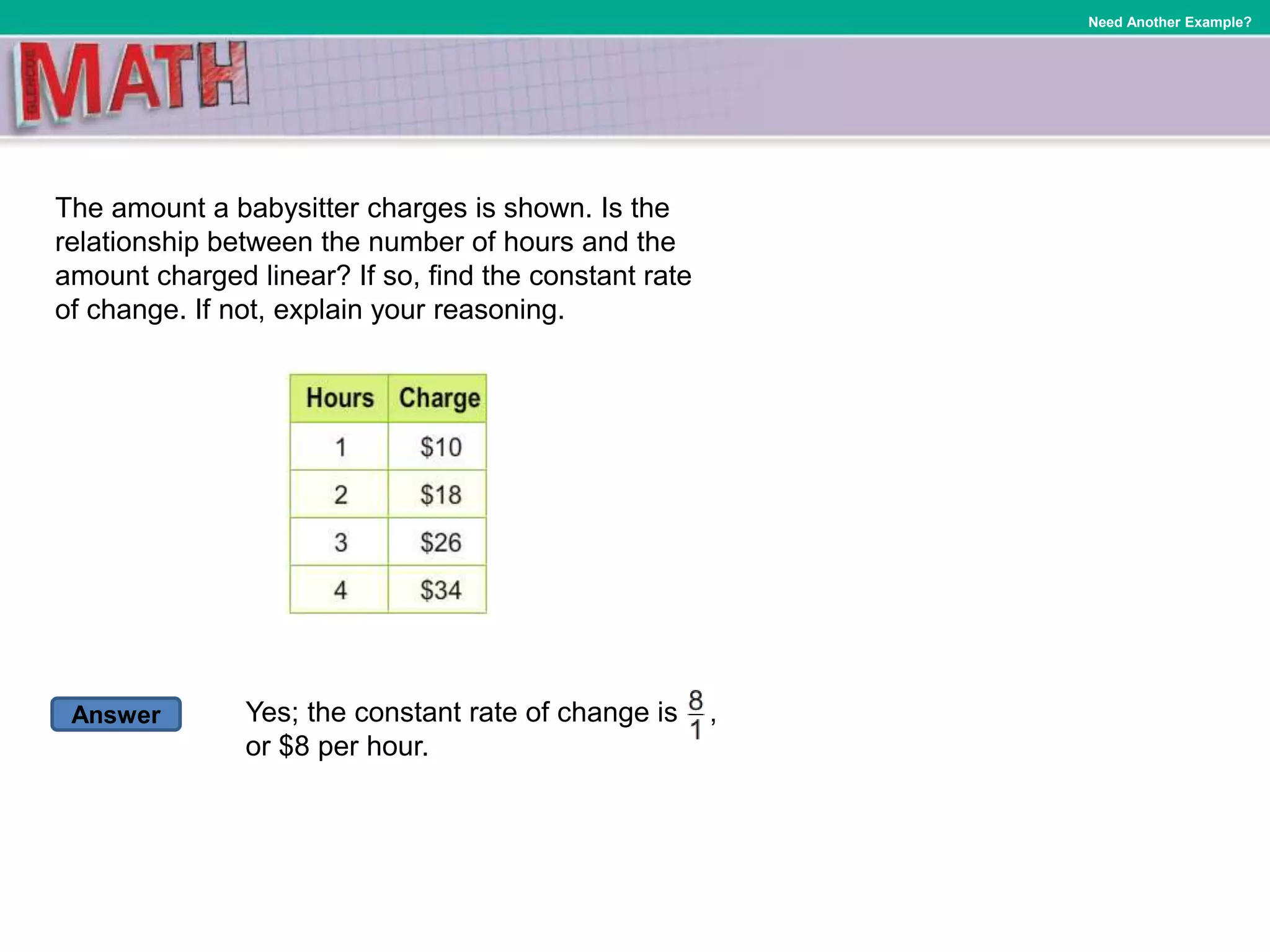
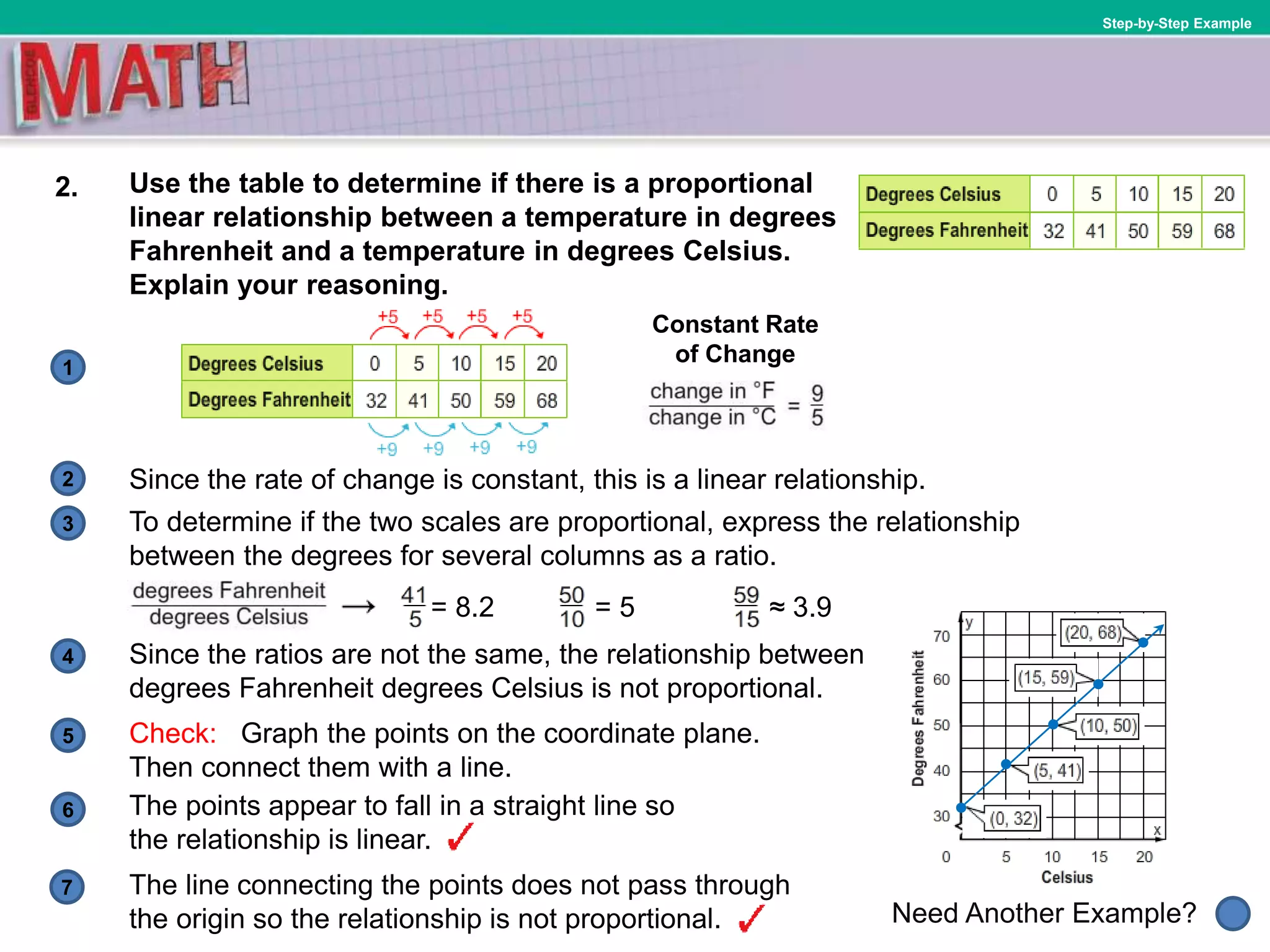
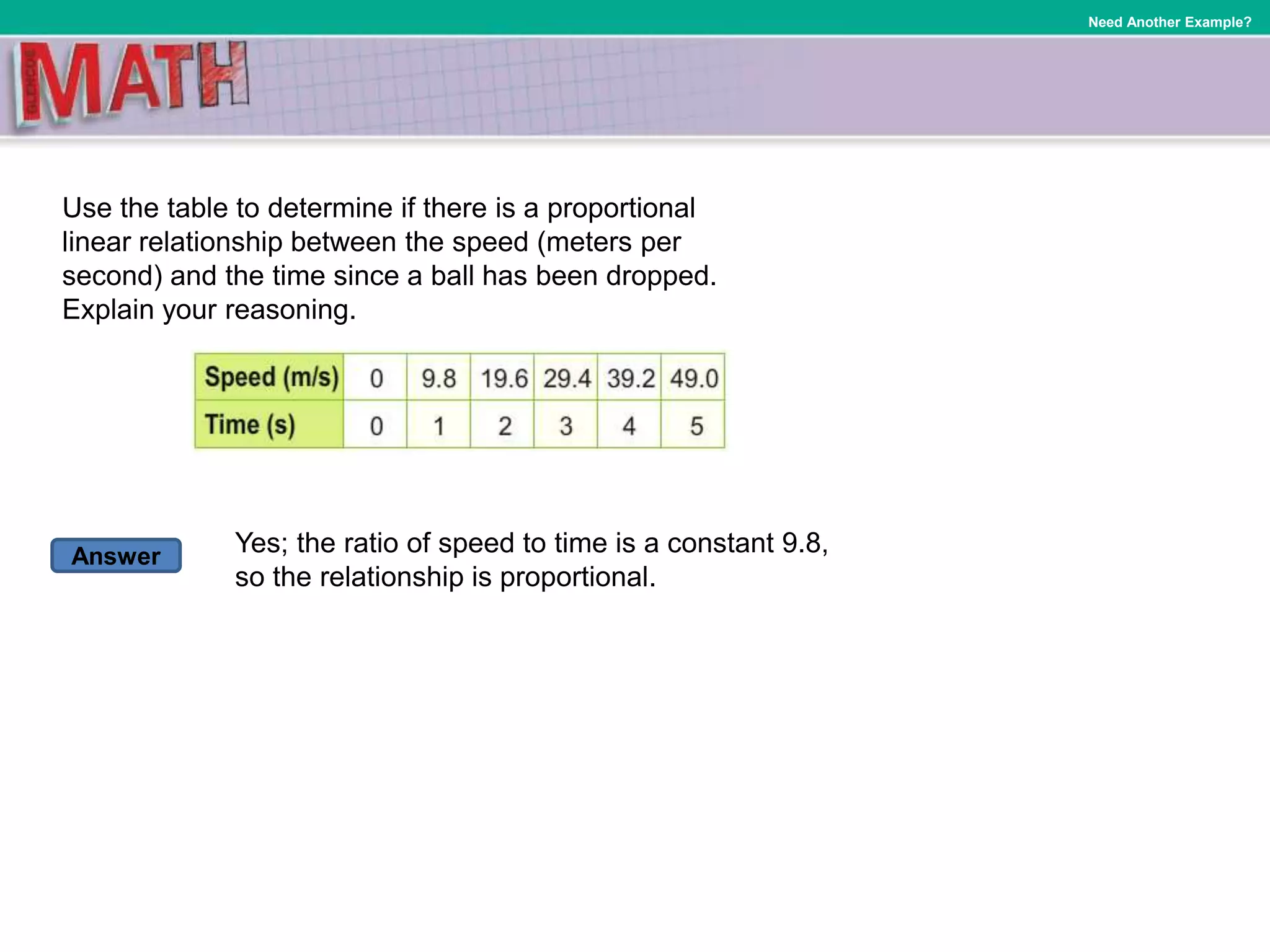
Here are some real-world examples of relationships that have a constant rate of change: - The speed of a car traveling at a constant velocity - As time passes, the car's position changes at a steady rate. - Interest accumulating in a bank account - The interest earned each time period is a constant percentage of the current balance. - Population growth over time - If the birth and death rates remain steady, the population will increase at a constant percentage each year. - Depreciation of an asset - Most assets lose value at a steady rate each year due to age and wear. - Temperature change from heating or cooling an object - The temperature will change at a steady rate until the object reaches equilibrium with its

1. Course 3, Lesson 3-1
Solve each equation. Check your solution.
1. 3(a + 3) = 12 2. 4(2y – 3) = 20
3. –5(m – 5) = 4(m + 1) 4.
5. Alexis has 6 more collector’s cards than Danny.
Together, the two friends have 24 cards. How many
cards does Alexis have?
1 2
( 25) ( 30)
5 5
z z  

2. Course 3, Lesson 3-1
ANSWERS
1. 1
2. 4
3.
4. –85
5. 15
7
3

3. WHY are graphs helpful?
Expressions and Equations
Course 3, Lesson 3-1

4. • Preparation for 8.EE.5
Graph proportional relationships, interpreting the unit rate as the slope of
the graph. Compare two different proportional relationships represented in
different ways.
Mathematical Practices
1 Make sense of problems and persevere in solving them.
3 Construct viable arguments and critique the reasoning of others.
4 Model with mathematics.
5 Use appropriate tools strategically.
Course 3, Lesson 3-1 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices and Council of
Chief State School Officers. All rights reserved.
Expressions and Equations

5. To
• determine if a relationship is linear,
• find the constant rate of change in a
linear relationship,
• determine if a relationship is proportional
Course 3, Lesson 3-1
Expressions and Equations

6. • linear relationship
• constant rate of
change
Course 3, Lesson 3-1
Expressions and Equations

7. Course 3, Lesson 3-1
Expressions and Equations
Words Two quantities a and b have a proportional linear
relationship if they have a constant ratio and a constant
rate of change.
Symbols is constant and is constant.
a
b
change in
change in
b
a

8. 1
Need Another Example?
2
Step-by-Step Example
1. The balance in an account after several transactions is shown. Is the
relationship between the balance and number of transactions linear? If
so, find the constant rate of change. If not, explain your reasoning.
As the number of transactions
increases by 3, the balance in
the account decreases by $30.
Since the rate of change is constant, this is a linear relationship. The
constant rate of change is or –$10 per transaction. This means that
each transaction involved a $10 withdrawal.

9. Answer
Need Another Example?
The amount a babysitter charges is shown. Is the
relationship between the number of hours and the
amount charged linear? If so, find the constant rate
of change. If not, explain your reasoning.
Yes; the constant rate of change is ,
or $8 per hour.

10. 1
Need Another Example?
2
3
4
5
6
Step-by-Step Example
2. Use the table to determine if there is a proportional
linear relationship between a temperature in degrees
Fahrenheit and a temperature in degrees Celsius.
Explain your reasoning.
Since the rate of change is constant, this is a linear relationship.
7
Constant Rate
of Change
To determine if the two scales are proportional, express the relationship
between the degrees for several columns as a ratio.
= 8.2 = 5 ≈ 3.9
Since the ratios are not the same, the relationship between
degrees Fahrenheit degrees Celsius is not proportional.
Check: Graph the points on the coordinate plane.
Then connect them with a line.
The points appear to fall in a straight line so
the relationship is linear.
The line connecting the points does not pass through
the origin so the relationship is not proportional.

11. Answer
Need Another Example?
Use the table to determine if there is a proportional
linear relationship between the speed (meters per
second) and the time since a ball has been dropped.
Explain your reasoning.
Yes; the ratio of speed to time is a constant 9.8,
so the relationship is proportional.

12. How did what you learned
today help you answer the
WHY are graphs helpful?
Course 3, Lesson 3-1
Expressions and Equations

13. How did what you learned
today help you answer the
WHY are graphs helpful?
Course 3, Lesson 3-1
Expressions and Equations
Sample answers:
• You can determine if a relationship is linear by looking
at the graph.
• You can use the graph to determine if a relationship is
proportional.

14. Give a real-world example
of a relationship that has a
constant rate of change.
Course 3, Lesson 3-1
Ratios and Proportional RelationshipsExpressions and Equations