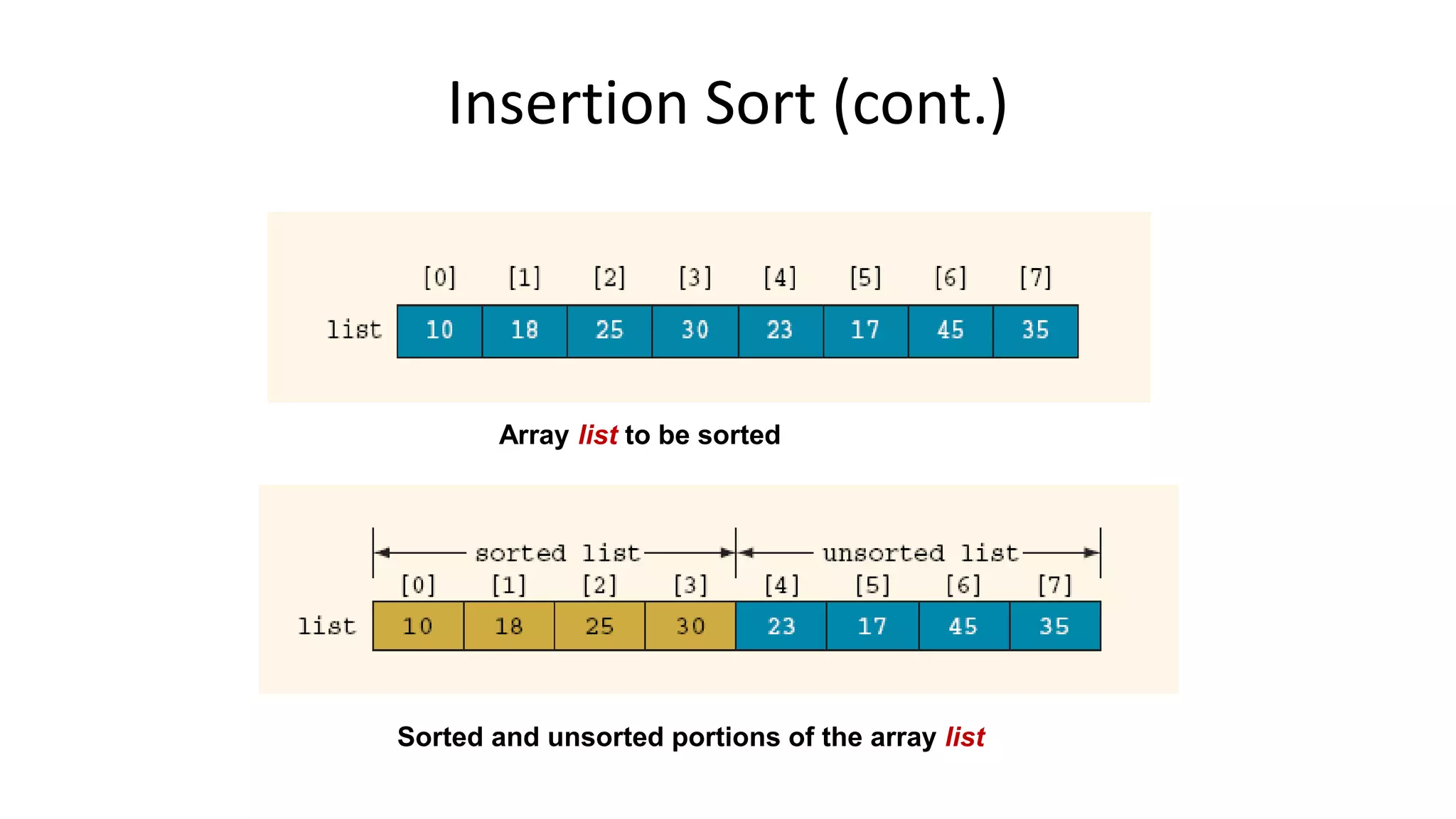
Insertion sort works by iterating through a list and inserting each element into its sorted position. It makes space by shifting larger elements to the right. For a randomly ordered array, insertion sort performs on average N2/4 key comparisons and exchanges in the worst case. However, it performs very efficiently on already sorted or partially sorted lists, requiring linear time. Insertion sort is well-suited for datasets where elements are mostly sorted or for very small lists.

1. Insertion Sort
 The algorithm that people often use to sort bridge hands is to consider the cards
one at a time, inserting each into its proper place among those already considered
(keeping them sorted).
 The insertion sort algorithm sorts the list by moving each element to its proper
place
 Works as follows:
 make space for the current item by moving larger items one position to the right,
before inserting the current item into the vacated position.

2. Insertion Sort (cont.)
Array list to be sorted
Sorted and unsorted portions of the array list

3. Insertion Sort (cont.)
Move list[4] into list[2]
Copy list[4] into temp

4. Insertion Sort (cont.)
Array list before copying list[3] into list[4], then list[2] into list[3]
Array list after copying list[3] into list[4], and then list[2] into list[3]

5. Insertion Sort (cont.)
Array list after copying temp into list[2]

6. Insertion Sort (cont.)

7. Insertion Sort (cont.)
• public static void insertionSort(int[] list, int listLength) {
• int firstOutOfOrder, location;
• int temp;
• for (firstOutOfOrder = 1; firstOutOfOrder < listLength;
firstOutOfOrder++)
• if (list[firstOutOfOrder] < list[firstOutOfOrder - 1]) {
• temp = list[firstOutOfOrder];
• location = firstOutOfOrder;
• do {
• list[location] = list[location - 1];
• location--;
• }
• while(location > 0 && list[location - 1] > temp);
• list[location] = temp;
• }
• } //end insertionSort

8. Insertion Sort (cont.)
 For randomly ordered arrays of length N, insertion sort makes:
 On the average:
 N2/4 key comparisons
 and N2/4 exchanges
 The worst case:
 N2/2 key comparisons
 and N2/2 exchanges
 The best case:
 N- 1 key comparisons
 and 0 exchanges

9. Insertion Sort (cont.)
 Insertion sort works well for certain types of nonrandom arrays that often arise in
practice, even if they are huge.
 Consider what happens when you use insertion sort on an array that is already
sorted.
 Each item is immediately determined to be in its proper place in the array, and the total
run time is linear.
 The same is true for arrays whose keys are all equal.

10. Insertion Sort (cont.)
 More generally, we consider the concept of a partially sorted array, as
follows:
 An inversion is a pair of keys that are out of order in the array.
 For instance, E X A M P L E has 11 inversions:
 E-A, X-A, X-M, X-P, X-L, X-E, M-L, M-E, P-L, P-E, and L-E
 If the number of inversions in an array is less than a constant multiple of the array size,
we say that the array is partially sorted.
 Typical examples of partially sorted arrays:
 An array where each entry is not far from its final position
 A small array appended to a large sorted array
 An array with only a few entries that are not in place

11. Insertion Sort (cont.)
 In summary: insertion sort is an excellent method for partially sorted arrays
and is also a fine method for tiny arrays.