1) The document discusses representing real-life situations using rational functions. It reviews polynomials and rational functions, and provides examples of expressing velocity and travel time as rational functions of variables like time and speed. 2) One example expresses the velocity of an object traveling 10 meters as a rational function of time. Another finds the time to travel 250 km from Manila to Baguio as a rational function of speed. 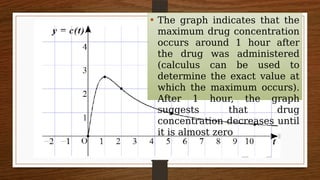3) Real-world contexts like drug concentration, organ pipe vibration, and travel time-speed relationships are used to demonstrate how rational functions can model real-life situations.

1. Representing
Real-Life
Situations Using
Rational
Functions

2. OBJECTIVE
• At the end of the lesson, the learner is able
• to represent real-life situations rational functions.

3. REVIEW
•Recall the definition of a
polynomial function.
A polynomial function p of degree n is a
function that can be written in the form
P(x)= + + + …….. +
•

4. • where
and n is a positive integer. Each addend of the sum is a term
of the polynomial function. The constants
are the coefficients. The leading coefficient is
. The leading term is
, and the constant term is

5. • A rational function is a function of the
form f(x) =
• where p(x) and q(x) are polynomial
functions, and q(x) is not the zero function
(i.e., q(x) 6 0). The domain of f(x) is all
values of x where q(x) 6= 0.
•

6. • Example 1. An object is to travel a
distance of 10 meters. Express velocity v as
a function of travel time t, in seconds.

9. • The graph indicates that the
maximum drug concentration
occurs around 1 hour after
the drug was administered
(calculus can be used to
determine the exact value at
which the maximum occurs).
After 1 hour, the graph
suggests that drug
concentration decreases until
it is almost zero

10. Solved Examples
• 1. In an organ pipe, the frequency f of
vibration of air is inversely proportional
to the length L of the pipe.1 Suppose
that the frequency of vibration in a 10-
foot pipe is 54 vibrations per second.
Express f as a function of L.

11. SOLUTION
• Since f is inversely proportional to L, then
f= , where k is the constant of
proportionality.
• If L = 10 then f = 54. Thus, . Thus 54 = =
k= 540, thus the function f(l) = represents
f as a function L.
•

12. 2. The distance from Manila to Baguio is around 250
kilometers.
• (a) How long will it take you to get to Baguio if
your average speed is 25 kilometers per hour? 40
kilometers per hour? 50 kilometers per hour?
• (b) Construct a function (s) , where (s) is the
speed of travel, that describes the time it takes to
drive from Manila to Baguio.

13. Solution
• (a) Distance is calculated as the product of
speed and time. So we can get the time by
dividing distance by the speed.
• 250 kilometers/ 25 kilometers per hour =
10 hours
• 250 kilometers/ 40 kilometers per hour =
6.25 hours

14. Solution
• ( (b) Since time is the quotient of distance
and speed, we can write out the function as
t(s) =
The distance is fixed at 250 kilometers so the
final function we have is
t(s) =
•