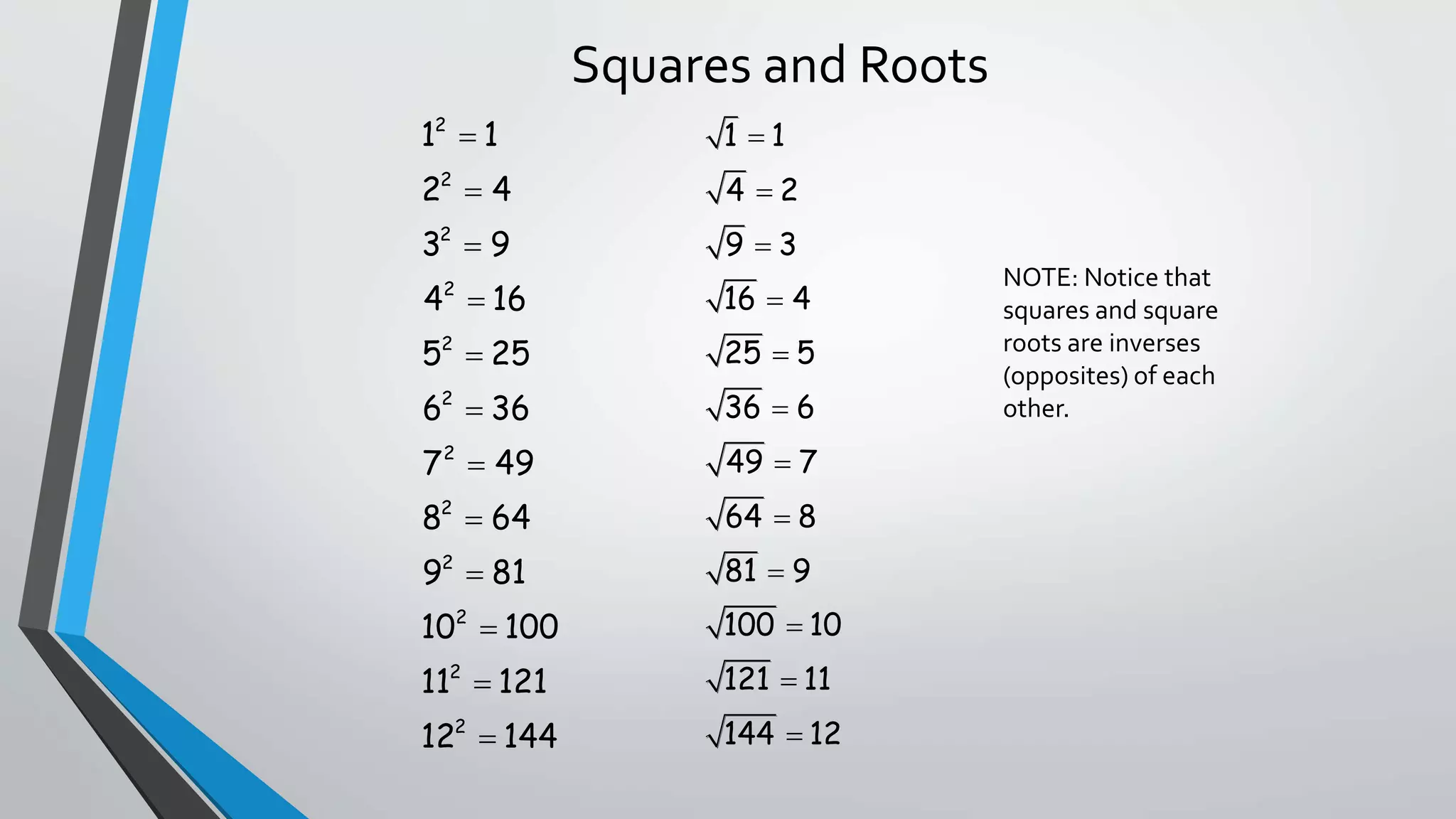
This document discusses rational and irrational numbers. It defines rational numbers as numbers that can be written as fractions, and irrational numbers as numbers that cannot be written as fractions, because they are either non-terminating decimals or decimals that do not repeat. The square roots of perfect squares are rational, while the square roots of numbers that are not perfect squares are irrational. Some examples of rational and irrational numbers are provided.

1. Irrational Numbers
By Group 3 Members:
Joshua Shajee
Venkat Sai (Leader)
Vignesh Kini
Lester Joel
Mayur Mahendra
Mir Khumail Ali

2. 1 2 3
2
1 1 2
2 4 2
3 9
The square of an integer is a perfect
square.
The opposite of squaring a number is
taking the square root.

3. Example
• For example
asks what number multiplied by itself is equal to 81? That
number is 9.
Is there another solution to that problem?
Yes, -9 is also a solution.
81

4. Simplify each square root
100
16
10
-4

5. Squares and Roots
2
2
2
2
2
2
2
2
2
2
2
2
1 1
2 4
3 9
4 16
5 25
6 36
7 49
8 64
9 81
10 100
11 121
12 144












1 1
4 2
9 3
16 4
25 5
36 6
49 7
64 8
81 9
100 10
121 11
144 12












NOTE: Notice that
squares and square
roots are inverses
(opposites) of each
other.

6. Estimating Square Roots
Once you memorized squares and their roots, we can estimate square roots
that are not perfect squares
• For example, what about
8

7. Estimating Square Roots
• We find the two perfect squares that are before and after
the square root of 8. . .
• and
• Look at them on a number line:
4 5
94
96 7 832
2 3

8. • We can see that is between 2 and 3 but
is closer to 3. We would say that is approximately 3.
Estimating square roots
4 5 96 7 832
2 3
8
8

9. TRY THIS:
Estimate to the nearest whole number
27
78
50
5
-9
7

10. • Rational number- can be written as a fraction
• Irrational number- cannot be written as a fraction
• because:
• it is a non-terminating decimal
• it is a decimal that does NOT repeat
* The square roots of ALL perfect squares are rational.
* The square roots of numbers that are NOT perfect
squares are irrational.

11. Identify each number as rational or
irrational.
2
81
0.53
0.627
13.875931...
Irrational
Rational
Rational
Rational
Irrational