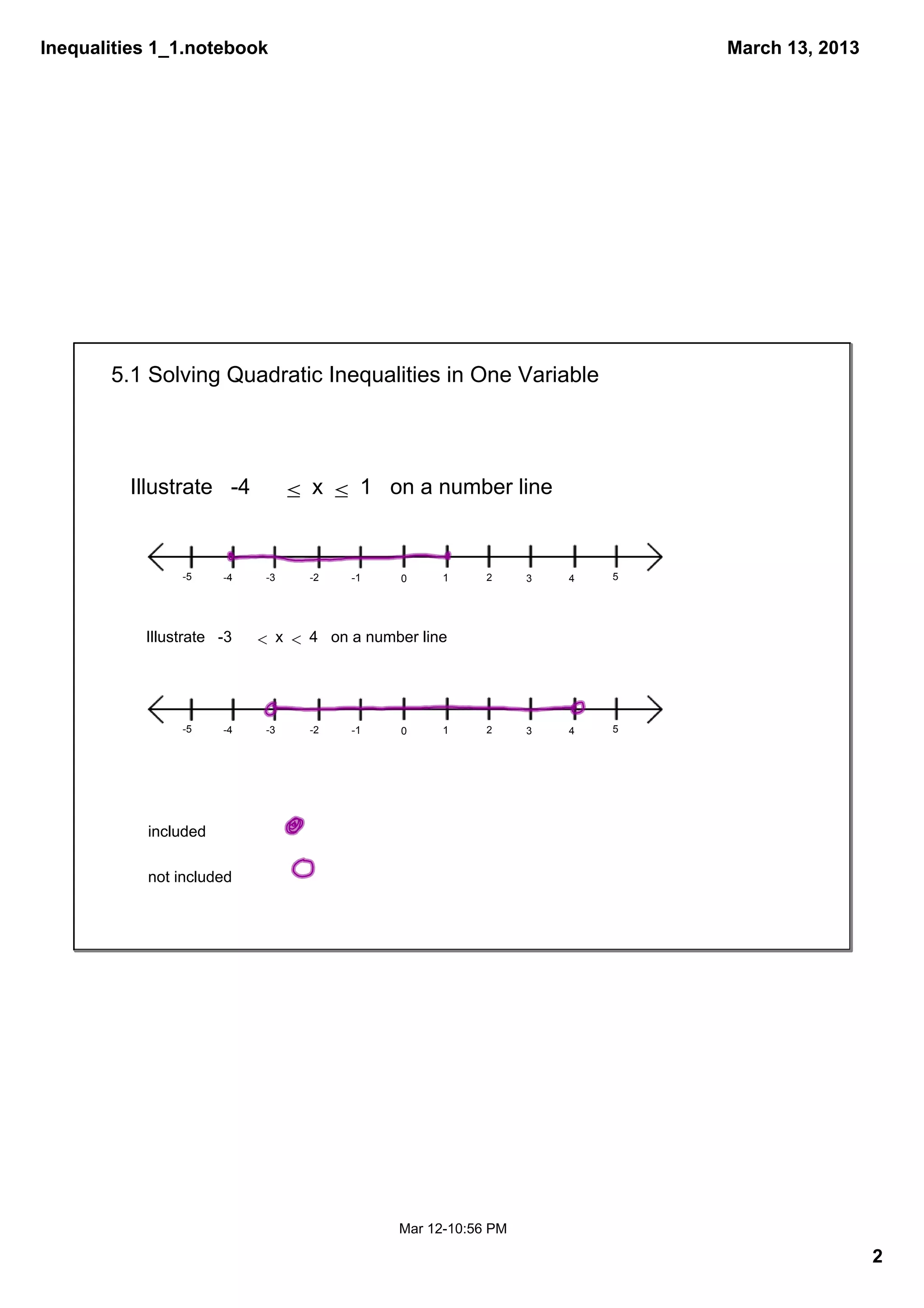
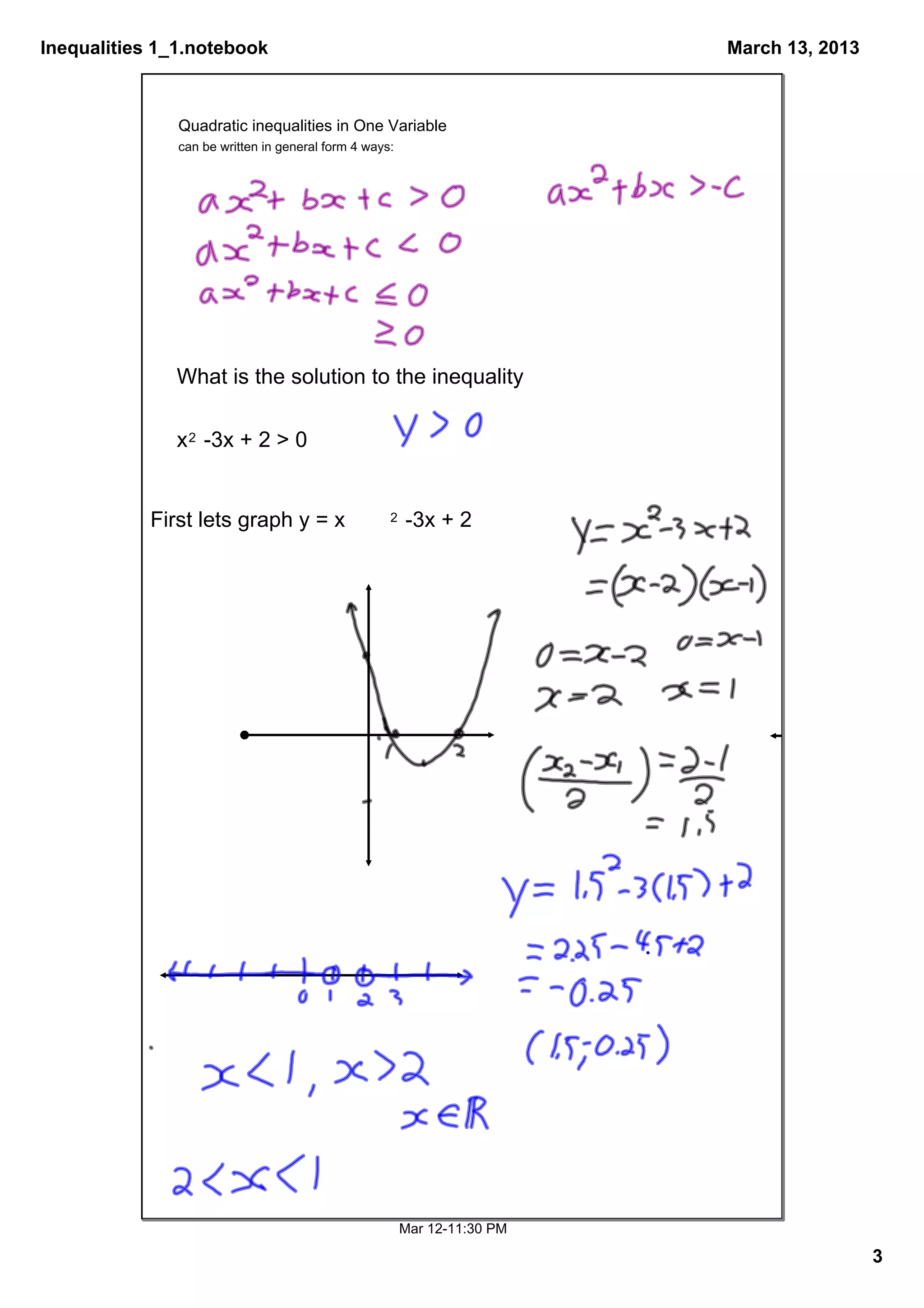
This document contains notes from a math class covering chapter 5 on graphing inequalities and systems of equations. It outlines the schedule for the chapter with topics being covered on Tuesdays and Thursdays. Examples are provided for solving quadratic inequalities in one variable by representing the solutions on number lines using critical values. The homework assignment lists specific problems from page 345 to complete.

1. Inequalities 1_1.notebook March 13, 2013
Chapter 5
Graphing Inequalities and Systems of Equations
Today ­ 5.1
Thursday ­ 5.2 (pi day??)
Monday ­ 5.3
Thursday ­ Test
Mar 12­10:33 PM
1

2. Inequalities 1_1.notebook March 13, 2013
5.1 Solving Quadratic Inequalities in One Variable
Illustrate ­4 ≤ x ≤ 1 on a number line
­5 ­4 ­3 ­2 ­1 0 1 2 3 4 5
Illustrate ­3 < x < 4 on a number line
­5 ­4 ­3 ­2 ­1 0 1 2 3 4 5
included
not included
Mar 12­10:56 PM
2

3. Inequalities 1_1.notebook March 13, 2013
Quadratic inequalities in One Variable
can be written in general form 4 ways:
What is the solution to the inequality
x 2 ­3x + 2 > 0
First lets graph y = x 2 ­3x + 2
Mar 12­11:30 PM
3

4. Inequalities 1_1.notebook March 13, 2013
x­intercepts of the graph of a quadratic function are called
critical values of the corresponding quadratic inequality.
These values are used to illustrate solutions to inequalities on
number lines
Example #1
Solve this inequality: 2x 2 ­ 7x > ­3
Represent the solution on a number line.
Mar 12­11:39 PM
4

5. Inequalities 1_1.notebook March 13, 2013
Example #2
Solve : 5x ≥ 2(x 2
-6) (not using a number line)
Mar 13­12:02 AM
5

6. Inequalities 1_1.notebook March 13, 2013
Example #3
The length of a rectangle is 2 cm greater than its width. The area of the
rectangle is at least 8 cm 2 . What are possible dimensions of the rectangle?
Mar 13­12:13 AM
6

7. Inequalities 1_1.notebook March 13, 2013
Homework
Page 345 #1­6, 8a, 10, 11, 13, 14
Mar 13­12:13 AM
7