4Probability and probability distributions.pdf

Measurements of Health and disease
Probability & probability distributions
1/3/2023 Probability & probability distributions 1
Emiru Merdassa(MSc, Assistant professor)

2
Definition
Probability: the chance that an uncertain event
will occur (always between 0 and 1)
0 ≤ P(A) ≤ 1 For any event A
Certain
Impossible
0.5
1
0
1/3/2023
Example:
• Physician may say that a patient has a 50-50 chance of
surviving a certain operation.
• 95% certain that a patient has a particular disease.
➢ Most people express probabilities in terms of
percentages.

Probability terms
• Outcomes: results of each trial
• Sample space: set of all possible outcome
• Sample points: elements of the sample space of
outcome
• Event: subset of the sample space
3
1/3/2023
(continued)

4
Important terms
• Intersection of Events – If A and B are two events in a sample
space S, then the intersection, A ∩ B, is the set of all outcomes in
S that belong to both A and B
(continued)
A B
AB
S
1/3/2023 Probability & probability distributions

5
Important terms
• Two events A and B are mutually exclusive if they cannot both
happen at the same time
• P (A ∩ B) = 0
(continued)
A B
S

6
Important terms
• Union of Events – If A and B are two events in a sample space S,
then the union, A U B, is the set of all outcomes in S that belong
to either A or B
(continued)
A B
The entire shaded area
represents
A U B
S

7
Important terms
• Events E1, E2, … Ek are Collectively Exhaustive events if E1 U E2 U
. . . U Ek = S
– i.e., the events completely cover the sample space
• The Complement of an event A is the set of all basic outcomes in
the sample space that do not belong to A. The complement is
denoted as ഥ
A
(continued)
A
S
A

8
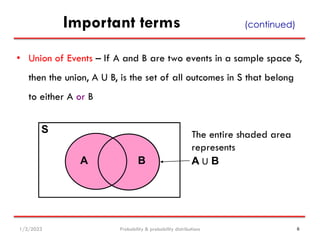
Example
Let the Sample Space be the collection of all possible
outcomes of rolling one die:
S = [1, 2, 3, 4, 5, 6]
Let A be the event “Number rolled is even”
Let B be the event “Number rolled is at least 4”
Then
A = [2, 4, 6] and B = [4, 5, 6]

9
(continued)
Example
S = [1, 2, 3, 4, 5, 6] A = [2, 4, 6] B = [4, 5, 6]
5]
3,
[1,
A =
6]
[4,
B
A =

6]
5,
4,
[2,
B
A =

S
6]
5,
4,
3,
2,
[1,
A
A =
=

Complements:
Intersections:
Unions:
[5]
B
A =

3]
2,
[1,
B =

10
Mutually exclusive:
o A and B are not mutually exclusive
• The outcomes 4 and 6 are common to both
Collectively exhaustive:
o A and B are not collectively exhaustive
• A U B does not contain 1 or 3
(continued)
Example
S = [1, 2, 3, 4, 5, 6] A = [2, 4, 6] B = [4, 5, 6]

Independent Events
• Two events A and B are independent if the probability of
the first one happening is the same no matter how the
second one turns out or
• The outcome of one event has no effect on the occurrence
or non-occurrence of the other.
P(A∩B) = P(A) x P(B) (Independent events)
P(A∩B) ≠ P(A) x P(B) (Dependent events)
Example:
O The outcomes on the first and second coin tosses are
independent
11

Continued…
Two categories of probability
1. Objective probability and
2. Subjective probability
1) Objective probability
a) Classical probability &
b) Relative frequency probability.
12

A) Classical Probability
• Is based on gambling ideas
• Example : Rolling a die
• There are 6 possible outcomes:
• Sample space = {1, 2, 3, 4, 5, 6}.
• Each is equally likely
• P(i) = 1/6, i=1,2,...,6.
→ P(1) = 1/6
→ P(2) = 1/6
…
→ P(6) = 1/6
SUM = 1
13

B) Relative Frequency Probability
• In the long run process.
• The proportion of times the event A occurs —in a large number
of trials repeated under essentially identical conditions
Definition:
• If a process is repeated a large number of times (n), and if an
event with the characteristic E occurs m times, the relative
frequency of E,
Probability of E = P(E) = m/n.
14

Example
• If you toss a coin 100 times and head comes up 40 times,
P(H) = 40/100 = 0.4.
• If we toss a coin 10,000 times and the head comes up 5562,
P(H) = 0.5562.
• Therefore, the longer the series and the longer sample size,
the closer the estimate to the true value.
15

Relative probability
• Since trials cannot be repeated an infinite number of
times, theoretical probabilities are often estimated by
empirical probabilities based on a finite amount of
data
Example:
➢ Of 158 people who attended a dinner party, 99 were ill.
➢ P (Illness) = 99/158 = 0.63 = 63%.
1/3/2023 16
(continued)

2. Subjective Probability
– Personalistic (represents one’s degree of belief in the occurrence
of an event).
– E.g., If someone says that he is 95% certain that a cure for AIDS
will be discovered within 5 years, then he means that:
– P(discovery of cure for AIDS within 5 years) = 95% = 0.95
– Although the subjective view of probability has enjoyed
increased attention over the years, it has not fully accepted by
scientists.
17

Properties of Probability
1. The numerical value of a probability always lies between 0 and 1,
inclusive(0  P(E)  1)
2. The sum of the probabilities of all mutually exclusive outcomes is
equal to 1.
P(E1) + P(E2 ) + .... + P(En ) = 1.
3. For two mutually exclusive events A and B,
P(A or B ) = P(AUB)= P(A) + P(B).
If not mutually exclusive:
P(A or B) = P(A) + P(B) - P(A and B)
1/3/2023 18

Properties of Probability
4. The complement of an event A, denoted by Ā or Ac, is the
event that A does not occur
• Consists of all the outcomes in which event A does NOT
occur: P(Ā) = P(not A) = 1 – P(A)
• Where Ā occurs only when A does not occur.
1/3/2023 19

Basic probability rules
1. Addition rule
➢ If events A and B are mutually exclusive:
P(A or B) = P(A) + P(B)
P(A and B) = 0
➢ More generally:
P(A or B) = P(A) + P(B) - P(A and B)
P(event A or event B occurs or they both occur)
20

Example
The probabilities representing years of schooling
completed by mothers of newborn infants
21
Mother’s education level Probability
≤ 8 years 0.056
9 to 11 years 0.159
12 years 0.321
13 to 15 years 0.218
≥16 years 0.230
Not reported 0.016

Continued
• What is the probability that a mother has
completed < 12 years of schooling?
P( 8 years) = 0.056 and
P(9-11 years) = 0.159
• Since these two events are mutually exclusive,
P( 8 or 9-11) = P( 8 U 9-11)
= P( 8) + P(9-11)
= 0.056+0.159
= 0.215
22

Exercise
i. Suppose two doctors, A and B, test all patients coming into a clinic for
syphilis. Let events A+ = {doctor A makes a positive diagnosis} and B+ =
{doctor B makes a positive diagnosis}.
ii. Suppose doctor A diagnoses 10% of all patients as positive, doctor B
diagnoses 17% of all patients as positive, and both doctors diagnose 8%
of all patients as positive.
➢ Suppose a patient is referred for further lab tests if either doctor A or B
makes a positive diagnosis.
 What is the probability that a patient will be referred for further lab
tests(P(Α+
∪ 𝐵+
)?
1/3/2023 23

Normal distributions
1/3/2023 24

The Normal distribution
• Normal distributions are recognized by their bell shape.
• A large percentage of the curve’s area is located near
its center and that its tails approach the horizontal axis
as asymptotes.
25

Normal distribution
1/3/2023 26
 Normal distributions are defined by:
, - < x < .
 where μ represents the mean of the distribution
and σ represents its standard deviation.
f(x) =
1
2
e
x-
2
 


−






1
2

 There are many different Normal distributions, each with
its own μ and σ, let X ~ N(μ, σ) represent a specific
member of the Normal distribution family.
 The symbol “~” is read as “distributed as.”
For example,
X ~ N(100, 15) is read as “X is a Normal random
variable with mean 100 and standard deviation 15.
1/3/2023 27

1. The mean µ tells you about location -
– Increase µ - Location shifts right
– Decrease µ – Location shifts left
– Shape is unchanged
2. The variance σ2 tells you about narrowness or flatness of the bell -
– Increase σ2 - Bell flattens. Extreme values are more likely
– Decrease σ2 - Bell narrows. Extreme values are less likely
– Location is unchanged
28

The normal distribution
Mean changes Variance changes
1/3/2023 29

30

Properties of the Normal Distribution
1. It is symmetrical about its mean, .
2. The mean, the median and mode are almost equal. It is
unimodal.
3. The total area under the curve about the x-axis is 1
square unit.
4. The curve never touches the x-axis.
5. As the value of  increases, the curve becomes more and
more flat and vice versa.
31

6. Perpendiculars of:
± 1SD contain about 68%;
±2 SD contain about 95%;
±3 SD contain about 99.7% of the area under the
curve.
7. The distribution is completely determined by the
parameters  and .
32

33

Standard Normal Distribution
It is a normal distribution that has a mean equal to 0 and a
SD equal to 1, and is denoted by N(0, 1).
The main idea is to standardize all the data that is given by
using Z-scores.
These Z-scores can then be used to find the area
(probability) under the normal curve.
34

Z - transformation
• If a random variable X~N(,) then we can transform
it to a SND with the help of Z-transformation
Z =
𝑿−

• Z represents the Z-score for a given x value
35

Continued
– Consider redefining the scale to be in terms of how many SDs
away from mean for normal distribution, μ=110 and σ = 15.
– SDs from mean using
𝒙−𝟏𝟏𝟎
𝟏𝟓
=
𝒙−

1/3/2023 36
Value x
50 65 80 95 110 125 140 155 171
-4 -3 -2 -1 0 1 2 3 4

Continued
– This process is known as standardization and gives the
position on a normal curve with μ=0 and σ=1, i.e., the
SND, Z.
– A Z-score is the number of standard deviations that a
given x value is above or below the mean.

Finding areas under the standard normal distribution curve
 The two steps are
Step 1 :
– Draw the normal distribution curve and shade the area.
Step 2:
– Find the appropriate figure in the Procedure Table and
follow the directions given.
1/3/2023 38

Procedure table
1/3/2023 39

Rules in computing probabilities
P[Z = a] = 0
P[Z ≤ a] obtained directly from the Z-table
P[Z ≥ a] = 1 – P[Z ≤ a]
P[Z ≥ -a] = P[Z ≤ +a]
P[Z ≤ -a] = P[Z ≥ +a]
P[a1 ≤ Z ≤ a2] = P[Z ≤ a2] – P[Z ≤ a1]

Example 1
Find the area to the left of z = 2.06.
Solution
Step 1:
Draw the figure.
Step 2:
We are looking for the area under the standard normal distribution
to the left of z =2.06. look up the area in the table. It is 0.9803.
Hence, 98.03% of the area is less than z =2.06.
1/3/2023 41

Example 2
Find the area to the right of z = -1.19
Solution
Step 1: Draw the figure.
Step 2 : We are looking for the area to the right of z = -1.19.
Look up the area for z = -1.19. It is 0.1170. Subtract it from one.
1- 0.1170 = 0.8830. Hence, 88.30% of the area under the
standard normal distribution curve is to the right of z = -1.19.
1/3/2023 42

Continued
Example 3:
What is the probability that a z picked at random from the
population of z’s will have a value between -2.55 and +2.55 ?
 Answer : P (-2.55 < z < +2.55)
= 0.9946 – 0.0054
= 0.9892
Example 4:
What proportion of z value are between -2.47 and 1.53?
 Answer : P (-2.47 ≤ z ≤ 1.53)
= 0.9370 – 0.0068
= 0.9302

Exercises
1. Find the area between z =1.68 and z =-1.37. Ans = 0.8682
2. Find the probability for each.
a) P(0 < z <2.32) = 0.4898
b) P(z < 1.65) = 0.9505
c) P(z >1.91)= 0.0281
3. Find two z values so that 48% of the middle area is bounded
by them?
1/3/2023 44

Thank you.
1/3/2023 45

4Probability and probability distributions.pdf

More Related Content

Similar to 4Probability and probability distributions.pdf

More from AmanuelDina

Recently uploaded

4Probability and probability distributions.pdf