1) Mathematics is found in many natural phenomena such as ratios, proportions, geometric shapes, symmetry, and fractals. Concepts like congruence and ratios are important in everyday activities. 2) Foams and bubbles exhibit mathematical properties like Plateau's laws which describe how soap films meet. Fractal patterns are seen in trees, ferns, coastlines, and other natural forms. 3) Symmetry is ubiquitous in nature from bilateral symmetry in animals to radial and rotational symmetries in plants and crystals. Snowflakes have sixfold symmetry while sea stars have fivefold symmetry.

1. Online assignment
Natural resources
Submitted by
ASWATHI.MS
REG NO: 13971004
MATHEMATICS OPTIONAL
KUCTE, KUMARAPURAM

2. Natural resources- Mathematical
aspects
found in Environmental phenomena
congruence,
similarity, ratio and proportion,
geometric shapes, symmetric property
etc

3. Natural resources
INTRODUCTION
Math is all around us, even in the kitchen. When cooking a meal, we
sometimes checks the recipe to measure the portion or double-check the ratio of
ingredients. Choosing between a cup of sugar or a half cup is a mathematical
decision. Even setting and checking the timer to make sure the dish cooks for the
appropriate amount of time requires math skills. When at the mall looking for an
outfit to wear, we use math. Patterns in nature are visible regularities of form found
in the natural world. These patterns recur in different contexts and can sometimes
be modelled mathematically.
congruence
The concept of congruence is not restricted to the study of geometry. it plays
an important role in everyday living. We may be able to buy a refill for our pen when
the ink runs dry. We use congruence to replace a worn out part of the car, looking for
the 'same part number'. In construction, they have to use the blocks of a 's tandard
size'. When using screws, we look for the kind of screw that we need and also
screwdriver that fits. In each of these examples, the idea of sameness of shape and
sizes applies.
Ratio and proportion
Ratios: Relationships between quantities: That ingredients have relationships to
each other in a recipe is an important concept in cooking. It's also an important math
concept. In math, this relationship between 2 quantities is called a ratio. If a recipe
calls for 1 egg and 2 cups of flour, the relationship of eggs to cups of flour is 1 to 2.
In mathematical language, that relationship can be written in two ways:

4. 1/2 or 1:2
Both of these express the ratio of eggs to cups of flour: 1 to 2. If you mistakenly alter
that ratio, the results may not be edible.
Working with proportion
All recipes are written to serve a certain number of people or yield a certain amount
of food. You might come across a cookie recipe that makes 2 dozen cookies, for
example. What if you only want 1 dozen cookies? What if you want 4 dozen
cookies? Understanding how to increase or decrease the yield without spoiling the
ratio of ingredients is a valuable skill for any cook.
Let's say you have a mouth-watering cookie recipe:
1 cup flour
1/2 tsp. baking soda
1/2 tsp. salt
1/2 cup butter
1/3 cup brown sugar
1/3 cup sugar
1 egg
1/2 tsp. vanilla
1 cup chocolate chips
This recipe will yield 3 dozen cookies. If you want to make 9 dozen cookies, you'll
have to increase the amount of each ingredient listed in the recipe. You'll also need to
make sure that the relationship between the ingredients stays the same. To do this,
you'll need to understand proportion. A proportion exists when you have 2 equal
ratios, such as 2:4 and 4:8. Two unequal ratios, such as 3:16 and 1:3, don't result in a
proportion. The ratios must be equal
Eg. Golden ratio

5. A golden rectangle with longer sidea and shorter side b, when placed adjacent to a
square with sides of length a, will produce a similar golden rectangle with longer
side a + b and shorter side a. This illustrates the relationship .
In mathematics, two quantities are in the golden ratio if their ratio is the same as the
ratio of their sum to the larger of the two quantities. The figure on the right illustrates
the geometric relationship. Expressed algebraically, for
quantities a and b with a > b > 0,
where the Greek letter phi (φ) represents the golden ratio. Its value is:
The golden ratio is also called the golden section (Latin: sectio aurea)
or golden mean. Other names include extreme and mean ratio, medial
section, divine proportion, divine section (Latin: sectio divina), golden
proportion, golden cut, and golden number.
GEOMETRY
Geometry is one of the oldest sciences and is concerned with questions of shape, size
and relative position of figures and with properties of space.Geometry is considered
an important field of study because of its applications in daily life.Geometry is
mainly divided in two ;
Plane geometry - It is about all kinds of two dimensional shapes such as lines,circles
and triangles.Solid geometry - It is about all kinds of three dimensional shapes like
polygons,prisms,pyramids,sphere and cylinder.
Role of geometry in daily life:- Role of geometry in the daily life is the foundation
of physical mathematics. A room, a car, a ball anything with physical things is
geometrically formed. Geometry applies us to accurately calculate physical spaces.n
the world , Anything made use of geometrical constraints this is important
application in daily life of geometry.
Example: Architecture of a thing, design, engineering, building etc.
Geometry is particularly useful in home building or improvement projects. If you
need to find the floor area of a house, you need to use geometry. If you want to
replace a piece of furniture, you need to calculate the amount of fabric you want, by

6. calculating the surface area of the furniture. Geometry has applications in hobbies.
The goldfish tank water needs to have a certain volume as well as surface area in
order for the fish to thrive. We can calculate the volume and surface area using
geometry
Bubbles, foam
A soap bubble forms a sphere, a surface with minimal area — the smallest
possible surface area for the volume enclosed. Two bubbles together form a more
complex shape: the outer surfaces of both bubbles are spherical; these surfaces are
joined by a third spherical surface as the smaller bubble bulges slightly into the larger
one.
A foam is a mass of bubbles; foams of different materials occur in nature.
Foams composed of soap films obey Plateau's laws, which require three soap films to
meet at each edge at 120° and four soap edges to meet at each vertex at the
tetrahedral angle of about 109.5°. Plateau's laws further require films to be smooth
and continuous, and to have a constant average at every point. For example, a film
may remain nearly flat on average by being curved up in one direction (say, left to
right) while being curved downwards in another direction (say, front to back).
Structures with minimal surfaces can be used as tents. Lord Kelvin identified the
problem of the most efficient way to pack cells of equal volume as a foam in 1887;
his solution uses just one solid, the truncated cubic honeycomb with very slightly
curved faces to meet Plateau's laws.
At the scale of living cells, foam patterns are common; radiolarians, sponge
spicules, silicoflagellate exoskeletons and the calcite skeleton of a sea urchin,
Cidaris rugosa, all resemble mineral casts of Plateau foam boundaries. The skeleton
of the Radiolarian, Aulonia hexagona, a beautiful marine form drawn by Haeckel,
looks as if it is a sphere composed wholly of hexagons, but this is mathematically
impossible. The Euler characteristic states that for any convex polyhedron, the
number of faces plus the number of vertices (corners) equals the number of edges
plus two. A result of this formula is that any closed polyhedron of hexagons has to
include exactly 12 pentagons, like a soccer ball, Buckminster Fuller geodesic dome,
or fullerene molecule. This can be visualised by noting that a mesh of hexagons is
flat like a sheet of chicken wire, but each pentagon that is added forces the mesh to
bend (there are fewer corners, so the mesh is pulled in).

7. 
Foam of soap bubbles: 4 edges meet at each vertex, at angles close to 109.5°, as in
two C-H bonds in methane.
Beautiful examples of nature’s self-similarity
In mathematics, a self-similar object is exactly or approximately similar to a
part of itself (i.e. the whole has the same shape as one or more of the parts). Many
objects in the real world, such as coastlines, are statistically self-similar: parts of
them show the same statistical properties at many scales. Self-similarity is a typical
. property of fractals
Cloud cotton
Trees, fractals:- Fractals are infinitely self-similar, iterated mathematical constructs
having fractal dimensions. Infinite iteration is not possible in nature so all 'fractal'
patterns are only approximate. For example, the leaves
of ferns and umbellifers(Apiaceae) are only self-similar (pinnate) to 2, 3 or 4 levels.
Fern-like growth patterns occur in plants and in animals
including bryozoa, corals, hydrozoa like the air fern, Sertularia argentea, and in non-living
things, notably electrical discharges. Lindenmayer system fractals can model
different patterns of tree growth by varying a small number of parameters including

8. branching angle, distance between nodes or branch points (internode length), and
number of branches per branch point.
Fractal-like patterns occur widely in nature, in phenomena as diverse as clouds, river
networks, geologic fault lines,mountains, coastlines, animal coloration, snow
flakes, crystals, blood vessel branching, and ocean waves.

Leaf of Cow Parsley,Anthriscus sylvestris, is 2- or 3-pinnate, not infinite

Fractal spirals:Romanesco broccolishowing self-similar form

Angelica flowerhead, a sphere made of spheres (self-similar)

Trees: Lichtenberg figure: high voltage dielectric breakdown in an acrylic polymer
block

9. 
Trees: dendritic Copper crystals (in microscope)
Symmetry Symmetry in biology, Floral symmetry and crystal symmetry
Symmetry is pervasive in living things. Animals mainly have bilateral or mirror
symmetry, as do the leaves of plants and some flowers such as orchids. Plants often
have radial or rotational symmetry, as do many flowers and some groups of animals
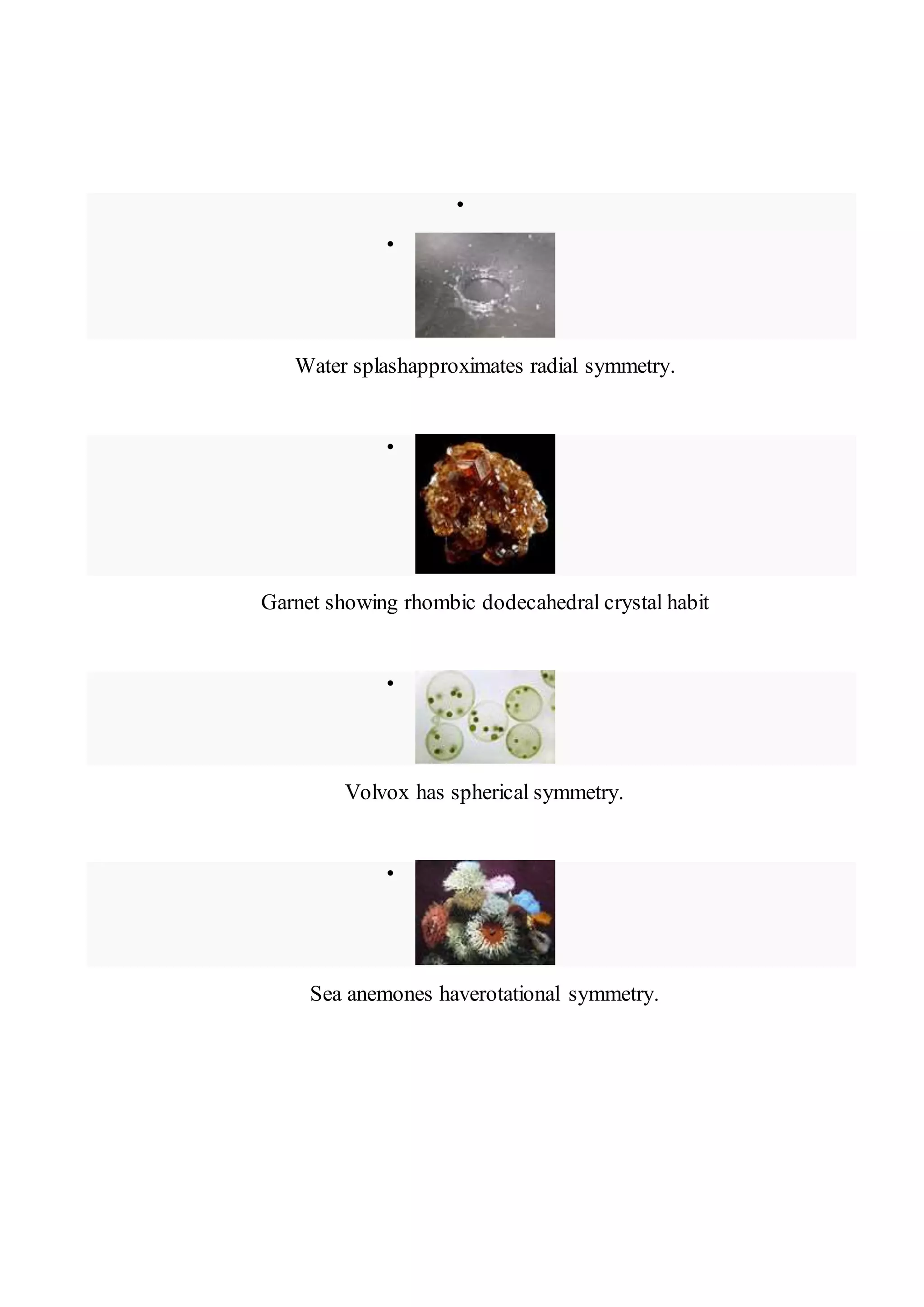
such. as sea anemones Fivefold symmetry is found in the echinoderms, the group that
includes starfish, sea urchins, and sea lilies.
Among non-living things, snowflakes have striking sixfold symmetry: each flake is
unique, its structure forming a record of the varying conditions during its
crystallisation, with nearly the same pattern of growth on each of its six
arms. Crystals in general have a variety of symmetries and crystal habits; they can be
cubic or octahedral, but true crystals cannot have fivefold symmetry
(unlike quasicrystals). Rotational symmetry is found at different scales among non-living
things including the crown-shaped splash pattern formed when a drop falls into
a pond,[28] and both the spheroidal shape and rings of a planet like Saturn.
Symmetry has a variety of causes. Radial symmetry suits organisms like sea
anemones whose adults do not move: food and threats may arrive from any direction.
But animals that move in one direction necessarily have upper and lower sides, head
and tail ends, and therefore a left and a right. The head becomes specialised with a
mouth and sense organs (cephalisation), and the body becomes bilaterally symmetric
(though internal organs need not be). More puzzling is the reason for the fivefold
(pentaradiate) symmetry of the echinoderms. Early echinoderms were bilaterally
symmetrical, as their larvae still are. Sumrall and Wray argue that the loss of the old
symmetry had both developmental and ecological causes.

Animals often show mirror or bilateral symmetry, like this tiger.

10. 
Echinoderms like thisstarfish have fivefold symmetry.

Fivefold symmetry can be seen in many flowers and some fruits like thismedlar.

Snowflakes have sixfold symmetry.

Each snowflake is unique but symmetrical.

Fluorite showing cubiccrystal habit

11. 

Water splashapproximates radial symmetry.

Garnet showing rhombic dodecahedral crystal habit

Volvox has spherical symmetry.

Sea anemones haverotational symmetry.

12. conclusion
Mathematics plays a key role in environmental studies, modeling, etc. Basic
mathematics - calculus, percents, ratios, graphs and charts, sequences, sampling,
averages, a population growth model, variability and probability - all relate to
current, critical issues such as pollution, the availability of resources, environmental
clean-up, recycling, CFC's, and population growth.
Mathematics plays a central role in our scientific picture of the world.
How the connection between mathematics and the world is to be accounted for
remains one of the most challenging problems in philosophy of science, philosophy
of mathematics, and general philosophy. A very important aspect of this problem is
that of accounting for the explanatory role mathematics seems to play in the account
of physical phenomena.
REFERENCES:
Stevens, Peter. Patterns in Nature, 1974.
Balaguer, Mark (12 May 2004, revised 7 April 2009). "Stanford Encyclopedia of
Philosophy"
WWW.WIKIPEDIA.COM .