The document discusses IEEE 754 floating-point representation, highlighting the two primary methods for storing real numbers—fixed point and floating point. It explains the components of floating point numbers, specifically focusing on the 32-bit and 64-bit formats, including the representation of numbers, special values, and calculations for examples. Various aspects such as the range of values, precision, and special conditions like denormalized numbers and NaN are also covered.






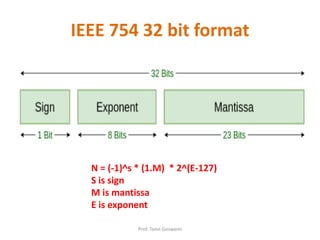







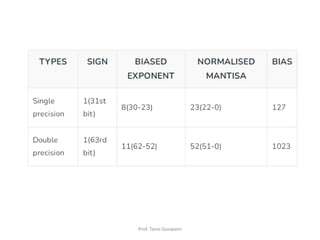


![Example
• The following scheme is used for floating point number
representation using 16 bits.
• Let the floating point number is represented as
N= (-1)^s * [ (1 + m * 2 ^(-9) ) ] * 2 ^ (e-31) , if
exponent is not equal to 111111 & 0 otherwise.
• What is the maximum difference between two
successive real numbers that can be represented in this
system?
Prof. Tanvi Goswami
Sign Exponent Mantissa
1 bit 6 bits 9 bits](https://image.slidesharecdn.com/3-231230081657-be8f4f6b/85/3-IEEE-754-FLOATING-POINT-For-Comp-ORG-pdf-18-320.jpg)





