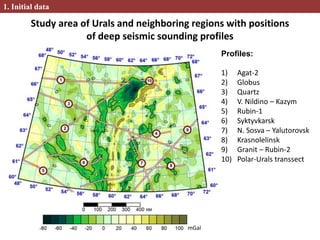
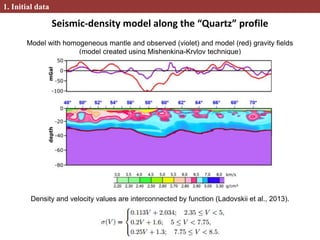
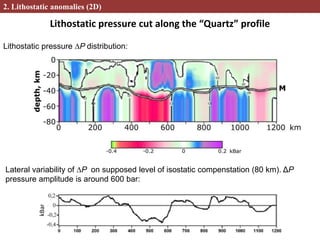
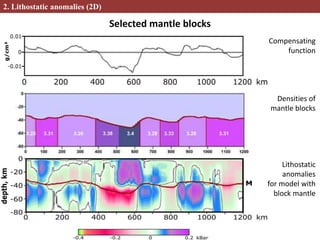
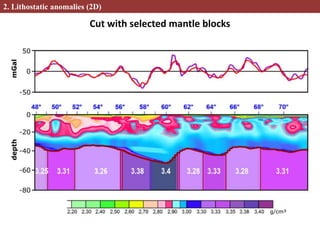
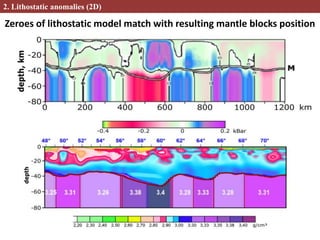
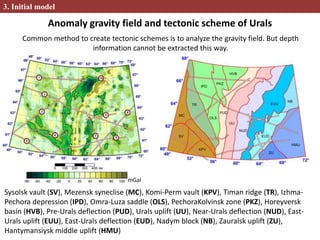
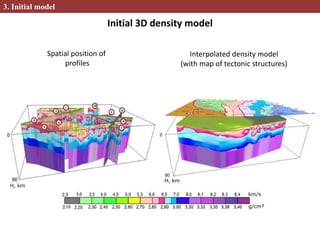
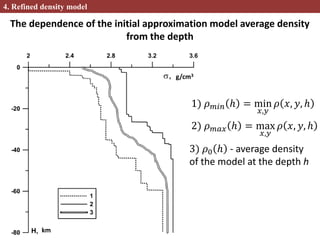
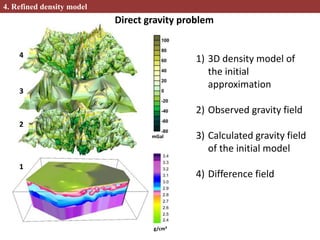
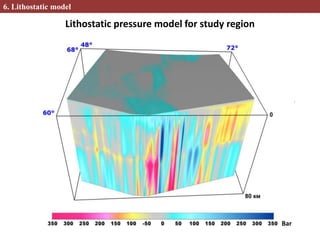
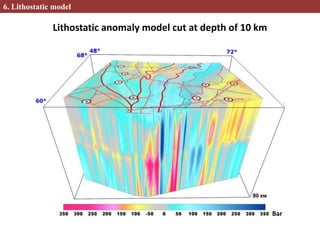
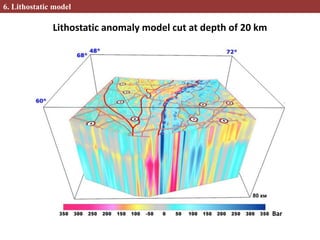
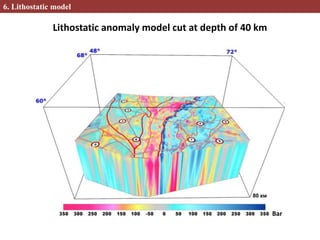
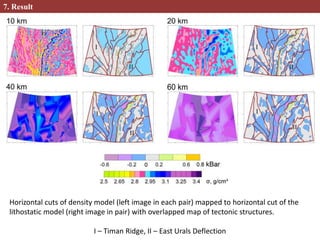
This document describes methods for creating 2D and 3D density block models based on the concept of isostasy from gravity survey data. Gravity surveys measure variations in the gravitational field, which are influenced by subsurface density distributions. The authors use lithostatic pressure anomalies calculated from fitted density models to select coherent density blocks within the lithosphere. In 2D, blocks are selected along seismic profiles where lithostatic pressure anomalies approach zero. In 3D, lithostatic pressure is calculated for different depth levels from a gridded density model, allowing blocks to be traced at various depths. Comparisons between the 3D lithostatic model and density model show blocks correspond to boundaries of tectonic structures mapped at the surface. This

1. Corr. Member of RAS, Prof. Petr Martyshko1,2
Dr. Igor Ladovskii1
Denis Byzov1
Alexander Tsidaev1,2
1Bulashevich Institute of Geophysics, Yekaterinburg, Russia
2Yeltsin Ural Federal University, Yekaterinburg, Russia
2D and 3D Density Block Models Creation
Based on Isostasy Usage
REIT'2017: 1st International Workshop on Radio Electronics & Information Technologies

2. Gravity survey (gravimetry)
Field of gravitational force has
tension approximately equal to
g = 9.8 m/s2
But this value is not a constant. All
the masses around have impacts on
the tension value. And the biggest
impact is from the masses below the
Earth surface level.
So the gravity field is dependent on
densities of the Earth rocks.
Interpreting measured gravity field
values, one can try to restore
possible density distribution under
the Earth surface.
0. Background
Image: PBG Ltd.

3. 0. Background
Isostasy is the state of gravitational equilibrium between Earth's crust and
mantle such that the crust "floats" at an elevation that depends on its
thickness and density.
Definition: Wikipedia, CC BY-SA 3.0
Image: Tasa Graphic Arts

4. Study area of Urals and neighboring regions with positions
of deep seismic sounding profiles
Profiles:
1) Agat-2
2) Globus
3) Quartz
4) V. Nildino – Kazym
5) Rubin-1
6) Syktyvkarsk
7) N. Sosva – Yalutorovsk
8) Krasnolelinsk
9) Granit – Rubin-2
10) Polar-Urals transsect
1. Initial data
mGal

5. Seismic-density model along the “Quartz” profile
1. Initial data
Density and velocity values are interconnected by function (Ladovskii et al., 2013).
Model with homogeneous mantle and observed (violet) and model (red) gravity fields
(model created using Mishenkina-Krylov technique)

6. 𝑔 𝑎=9,80665 m/s2 is mean value of gravity acceleration.
∆𝑃 𝑥, 𝑧 = 𝑃 𝑥, 𝑧 − 𝑃0 𝑧 = 𝑔 𝑎
𝑧
0
𝜌 𝑥, 𝜁 − 𝜌0 𝜁 𝑑𝜁
Lithostatic pressure anomalies
The lithostatic anomaly is defined as difference between the lithostatic and
hydrostatic pressures on given depth level.
Lithostatic pressure is calculated by values of fitted densities. Hydrostatic
pressure is calculated by mean density value 𝜌0 𝑧 on every hypsometric level.
For every 𝑧 depth value the deviation ∆𝑃 𝑥, 𝑧 of lithostatic pressure 𝑃 𝑥, 𝑧
from its mean (hydrostatic) value 𝑃0 𝑧 is calculated.
2. Lithostatic anomalies (2D)

7. Lithostatic pressure cut along the “Quartz” profile
2. Lithostatic anomalies (2D)
Lateral variability of ∆P on supposed level of isostatic compenstation (80 km). ΔР
pressure amplitude is around 600 bar:
Lithostatic pressure ∆P distribution:
kBar

8. Compensating function
2. Lithostatic anomalies (2D)
To rearrange mantle density to satisfy isostatic equilibrium condition on the level of
80 km we introduced compensating function.
Compensator 𝜌 𝑥 shows which density value should be added (or subtracted) to
the layer between Mohorovicic discontinuity HM and the lower boundary of layer H.

9. Selected mantle blocks
2. Lithostatic anomalies (2D)
Densities of
mantle blocks
Lithostatic
anomalies
for model with
block mantle
Compensating
function

10. Cut with selected mantle blocks
2. Lithostatic anomalies (2D)

11. Zeroes of lithostatic model match with resulting mantle blocks position
2. Lithostatic anomalies (2D)

12. 3D case
3. Initial model

13. Anomaly gravity field and tectonic scheme of Urals
3. Initial model
Sysolsk vault (SV), Mezensk syneclise (MC), Komi-Perm vault (KPV), Timan ridge (TR), Izhma-
Pechora depression (IPD), Omra-Luza saddle (OLS), PechoraKolvinsk zone (PKZ), Horeyversk
basin (HVB), Pre-Urals deflection (PUD), Urals uplift (UU), Near-Urals deflection (NUD), East-
Urals uplift (EUU), East-Urals deflection (EUD), Nadym block (NB), Zauralsk uplift (ZU),
Hantymansiysk middle uplift (HMU)
mGal
Common method to create tectonic schemes is to analyze the gravity field. But depth
information cannot be extracted this way.

14. Initial 3D density model
Interpolated density model
(with map of tectonic structures)
Spatial position of
profiles
3. Initial model

15. The dependence of the initial approximation model average density
from the depth
g/cm3
km
1) 𝜌 𝑚𝑖𝑛 ℎ = min
𝑥,𝑦
𝜌 𝑥, 𝑦, ℎ
2) 𝜌 𝑚𝑎𝑥 ℎ = max
𝑥,𝑦
𝜌 𝑥, 𝑦, ℎ
3) 𝜌0 ℎ - average density
of the model at the depth h
4. Refined density model

16. Direct gravity problem
mGal
1
1) 3D density model of
the initial
approximation
2) Observed gravity field
3) Calculated gravity field
of the initial model
4) Difference field
g/cm³
2
3
4
4. Refined density model

17. “Upward” continuation process (integral formula):
dxdy
hyx
yxgh
hg  



 
 2
3
))()((
)0,,(
2
),,( 222


z=0
z=-h
z=h
Splitting the field difference on density model layers
),,(
)4)()((
),,(
2
2
2
3222
hgdxdy
hyx
hyxgh





 




Field at the height (+h) 𝑔 , , ℎ = 𝑈 ,  – a known quantity
Field at the depth (-h) 𝑔 , , −ℎ = 𝑢 ,  – unknown quantity
 

,
)4)()((
),(
2
2
2
3222
Udxdy
hyx
yxuh


 




𝐾 + 𝜶𝐸 𝑢 = 𝑈
“Downward” continuation process (integral equation):
4. Refined density model

18. Transformation of the field difference on heights with step 1 km
∆𝑔, mGal
40 km
80 km
0 km
Field of layer below H = 00 km
g[-72; 101] mGal
4. Refined density model

19. Transformation of the field difference on heights with step 1 km
∆𝑔, mGal
Field of layer below H = 05 km
g[-24; 44] mGal
40 km
80 km
0 km
4. Refined density model

20. Transformation of the field difference on heights with step 1 km
∆𝑔, mGal
Field of layer below H = 20 km
g[-43; 51] mGal
40 km
80 km
0 km
4. Refined density model

21. Transformation of the field difference on heights with step 1 km
∆𝑔, mGal
Field of layer below H = 40 km
g[-15; 15] mGal
40 km
80 km
0 km
4. Refined density model

22. Transformation of the field difference on heights with step 1 km
∆𝑔, mGal
Field of layer below H = 80 km
g[-8; 7] mGal
40 km
80 km
0 km
4. Refined density model

23. 4. Refined density model
mGal
g/cm3
Resulting 3D model with fitted densities

24. Anomaly lithostatic pressure
5. Lithostatic anomalies (3D)
Gravity anomalies contain integral information on density inhomogeneities for all
lithosphere depth levels. Thus, blocks selected by the gravity field could not be split by
depth. Moreover, these blocks are usually invisible in horizontal maps of density
distribution.
We propose to use integral characteristics: masses of prismatic elements of 3D density
grid. For each depth level, masses of prisms located above are calculated and the sum
then converted to lithostatic pressure. In lithostatic model the blocks of Earth crust
become mode visible and can be traced on different depth levels.
Similarly to 2D case, we introduce anomaly lithostatic pressure ∆𝑃 𝑥, 𝑦, 𝑧 as difference
between a lithostatic pressure and the hydrostatic one, calculated on given depth.
∆𝑃 𝑥, 𝑦, 𝑧 = 𝑃 𝑥, 𝑦, 𝑧 − 𝑃0 𝑧 = 𝑔 𝑎
𝑧
0
𝜌 𝑥, 𝑦, 𝜁 − 𝜌0 𝜁 𝑑𝜁

25. 6. Lithostatic model
Bar
Lithostatic pressure model for study region

26. Lithostatic anomaly model cut at depth of 10 km
6. Lithostatic model
Bar

27. 6. Lithostatic model
Lithostatic anomaly model cut at depth of 20 km
Bar

28. 6. Lithostatic model
Lithostatic anomaly model cut at depth of 40 km
Bar

29. Horizontal cuts of density model (left image in each pair) mapped to horizontal cut of the
lithostatic model (right image in pair) with overlapped map of tectonic structures.
I – Timan Ridge, II – East Urals Deflection
7. Result

30. 8. Conclusion
• Matching of 3D lithostatic model with density model allowed us to select large deep
inhomogeneities in the upper lithosphere.
• Distribution of lithostatic pressure on horizontal cuts qualitatively matches the map of
tectonic structures, which was created by potential fields.
• Block structures positions coincides with the deep fault boundaries of collision
structures: East boundary of Timan ridge, Pechora-Kolvinsk zone, Near-Urals Deflection,
Western edge of Tagil deflection (Main Urals Fault) and zone of East-Urals uplift and
East-Urals deflection conjunction.
• Such a separation of continual density model to separate layers and blocks of different
organization level allows one to build seismic-gravity model of layers and blocks for the
Earth crust in a study region.
Conclusion

31. 9. Literature
Ladovsky, I.V., Martyshko, P.S., Druzhinin, V.S., Byzov, D.D., Tsidaev, A.G., Kolmogorova V.V.: Methods
and results of crust and upper mantle volume density modeling for deep structure of the Middle Urals
region.
Ural Geophysical Messenger. 2(22), 31-45 (2013) [in Russian]
Martyshko, P.S., Ladovskii, I.V., Byzov, D.D.: Solution of the Gravimetric Inverse
Problem Using Multidimensional Grids.
Doklady Earth Sciences. 450, Part 2, 666-671 (2013)
Martyshko, P.S., Ladovskiy, I.V., Byzov, D.D.: Stable methods of interpretation of gravimetric data.
Doklady Earth Sciences. 471, Issue 2, 1319{1322 (2016)
Martyshko, P.S., Ladovskiy, I.V., Fedorova, N.V., Byzov, D.D., Tsidaev, A.G.: Theory and methods of
complex interpretation of geophysical data. UrO RAN, Ekaterinburg (2016) [in Russian]
http://igeoph.net/book.pdf

32. Thank you for your attention
10. Questions?